前言
隨著技術的發展,基于 GPU 的渲染技術得到了廣泛應用,日常生活中常見的 3D 動畫和游戲都是通過計算機渲染技術來實現。當前主要的 3D 渲染模型包括光柵化渲染和光線追蹤兩大類,本文主要圍繞光柵化渲染進行介紹,描述了簡單場景下3D渲染過程,主要幫助讀者了解基于光柵化的 3D 渲染原理及過程。本文為系列文章,并在下一篇系列文章中以 Intel Gen12 為例,講述 GPU 一些基本硬件單元及如何利用硬件加速渲染過程。希望通過這種軟件計算 + 硬件實現的方式,讓大家了解 GPU 3D 渲染原理及過程。
在開始正式的介紹前,有以下幾點說明:
在渲染過程中,涉及到向量、矩陣等數學知識不再闡述。在后面用到的時候會有提及。
文中選擇了一個簡單的模型場景,過程也盡可能簡化。旨在重點講述光柵化流程,便于讀者理解。
推薦課程 GAMES101,文章后面用到的一些圖片出自該課件。
光柵化過程
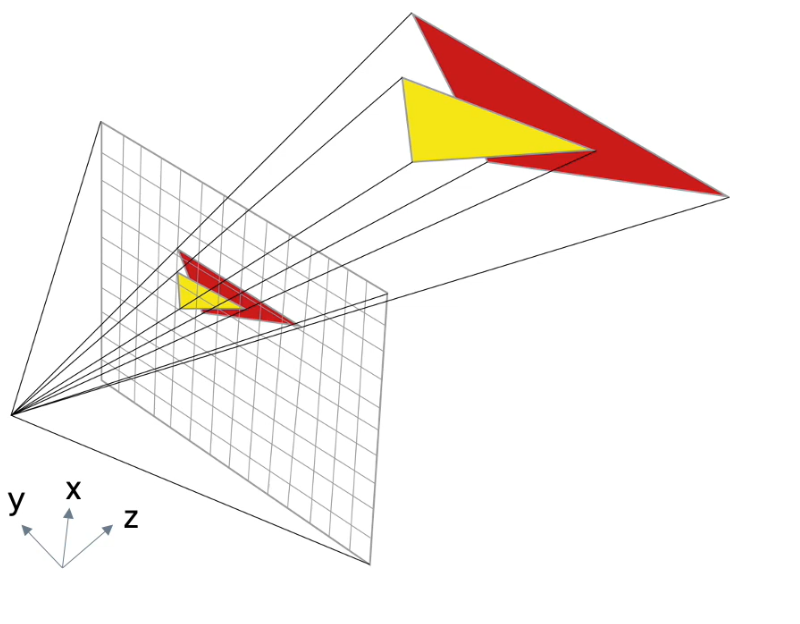
圖0 光柵化示意圖
圖0 是光柵化的一個簡易圖,其中光柵化主要完成以下兩個功能:
將幾何圖元(三角形/多邊形)投影到屏幕上
將投影之后的圖元分解成片段
模型建立
下文開始舉例說明光柵化過程,為了更簡單的說明光柵化,我們選用相對簡單的模型,在三維空間中存在兩個三角形,其中三角形1 三個頂點坐標分別為(-2, 0, -2)、(2, 0, -2)、(0, 2, -2),三角形2 三個頂點坐標分別為(-1, 0.5, -20)、(2.5, 1, -20)、(3, -1.5, -20),之所以后面三角形 z 絕對值比較大,是為了后面觀察透視投影近大遠小的效果。在模型中,除了被觀察物體,還需要確認觀察點的位置,這里將相機放在位置(0, 0, 0),觀察方向是 z 軸負方向(z-),向上向量為 y 軸正向(y+)。模型如圖1所示: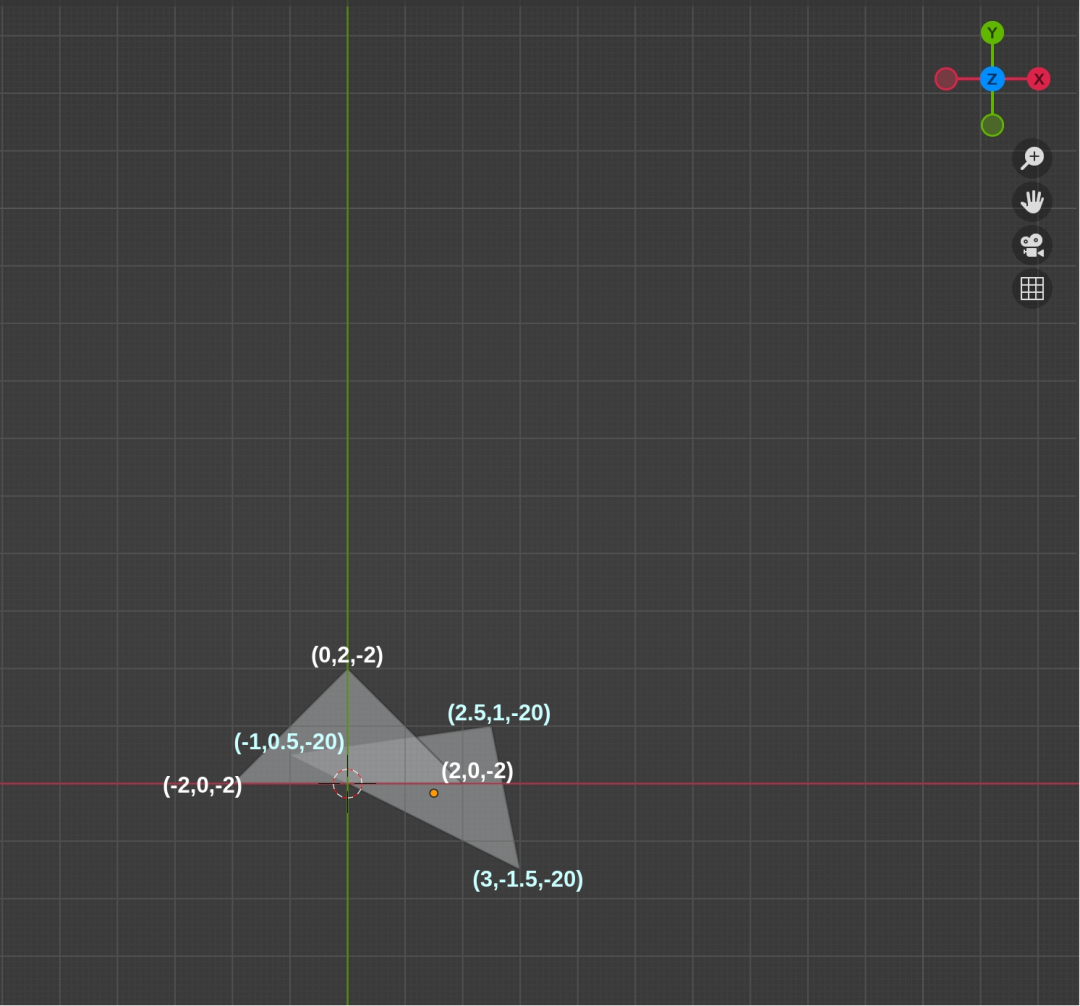
圖1 模型頂視圖
物體和相機的位置已經放好了,那么我們接下來要做的就是要將相機實際看到的內容最終顯示到屏幕上。模型是三維的,而最終的成像是二維,所以這其中必然要有投影操作。
正交投影和透視投影
先來看一下透視投影和正交投影的效果圖:
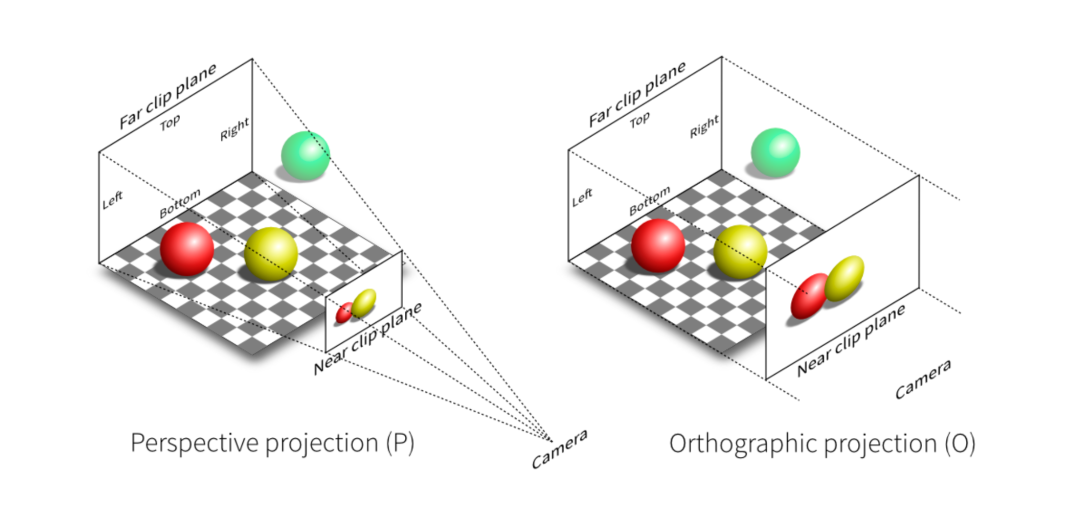
圖2 透視投影 & 正交投影
對比正交投影和透視投影效果可以發現,透視投影的結果會有近大遠小的效果,而正交投影不會。正交投影中,以平行線投射方式投影,在工程制圖等場景應用廣泛。透視投影這種近大遠小的效果和人眼成像效果基本一致,后面主要針對透視投影講解。也正是因為這種效果,才有了"道理我都懂,可是為什么鴿子這么大"這個梗。綠色的球在視野之外,會被裁剪掉。透視投影本質就是對一個平截頭體及平截頭體里的物體(圖2左半邊虛線內部分,包含紅球和黃球)做變換,這時候平截頭體會被壓成長方體(圖3-1),變換后的物體也包含在這個長方體中,最終長方體標準化生成[-1, 1] ^ 3標準正方體(圖3-2),然后再針對[x, y]平面做投影,投影過程中z軸作為深度覆蓋參考。
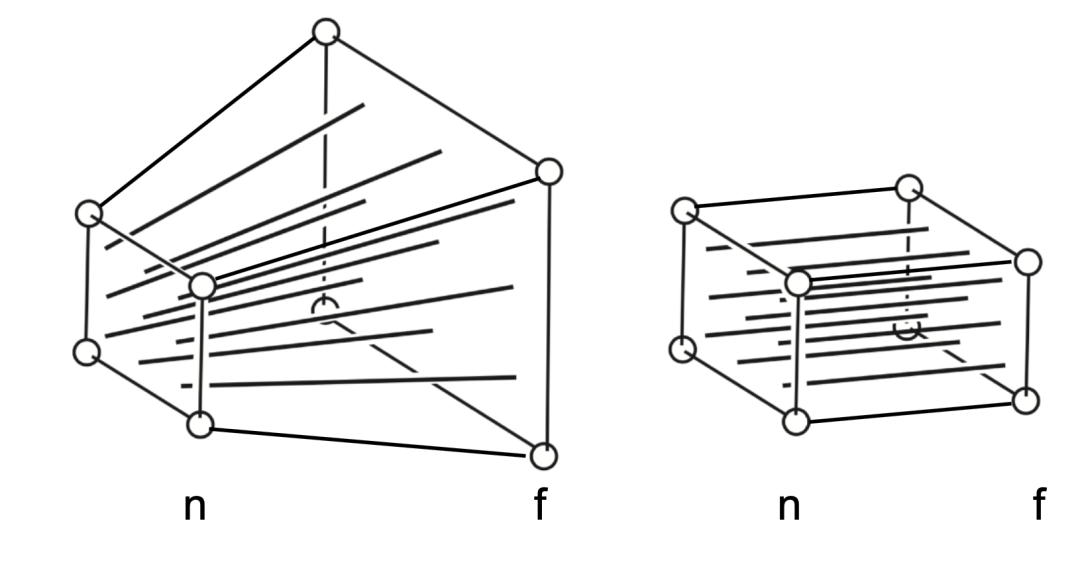
圖3-1 透視壓縮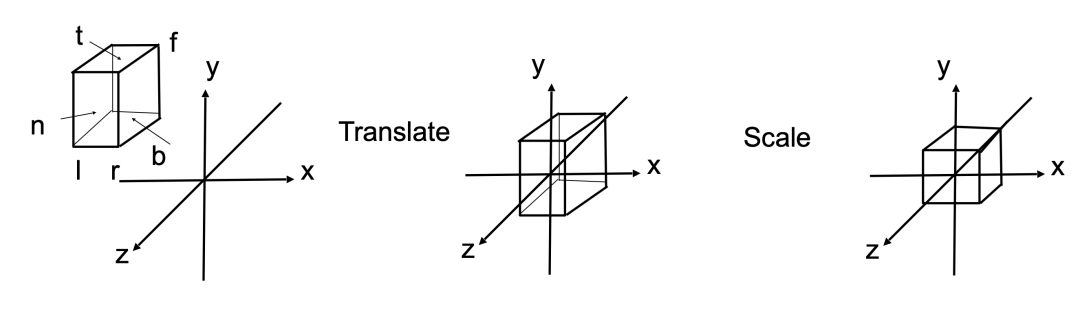
圖3-2 坐標標準化
再看下面兩個效果圖: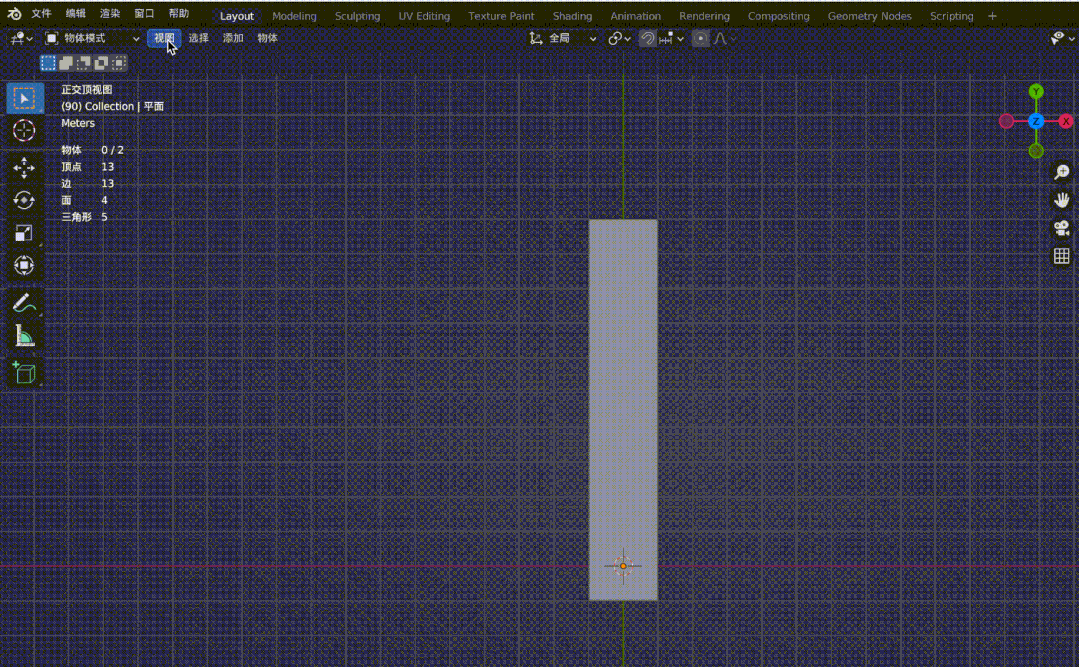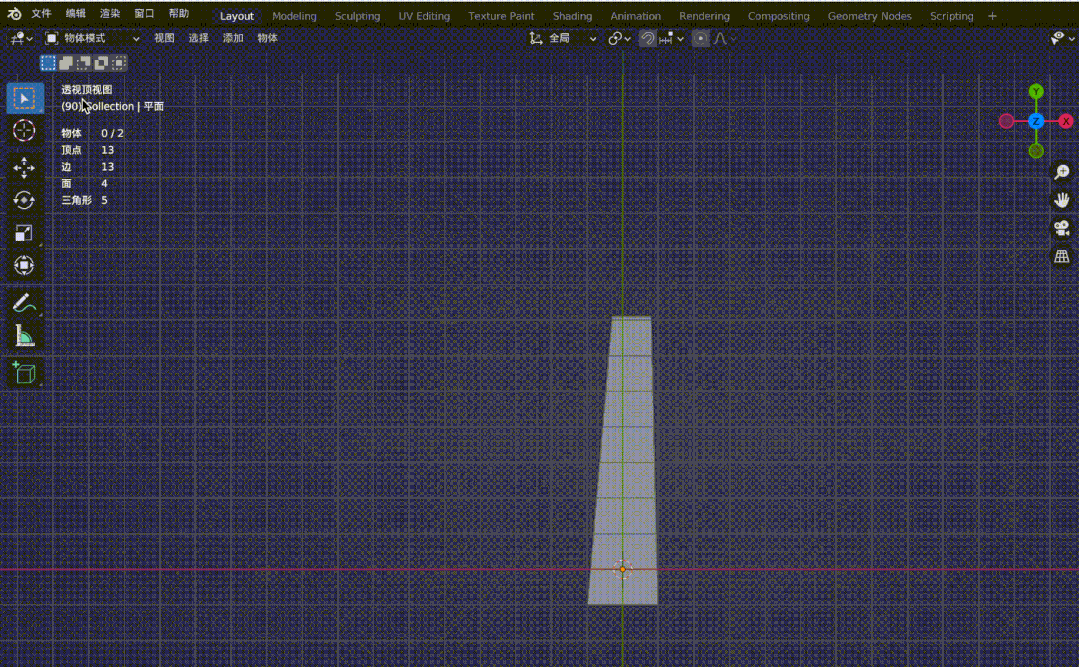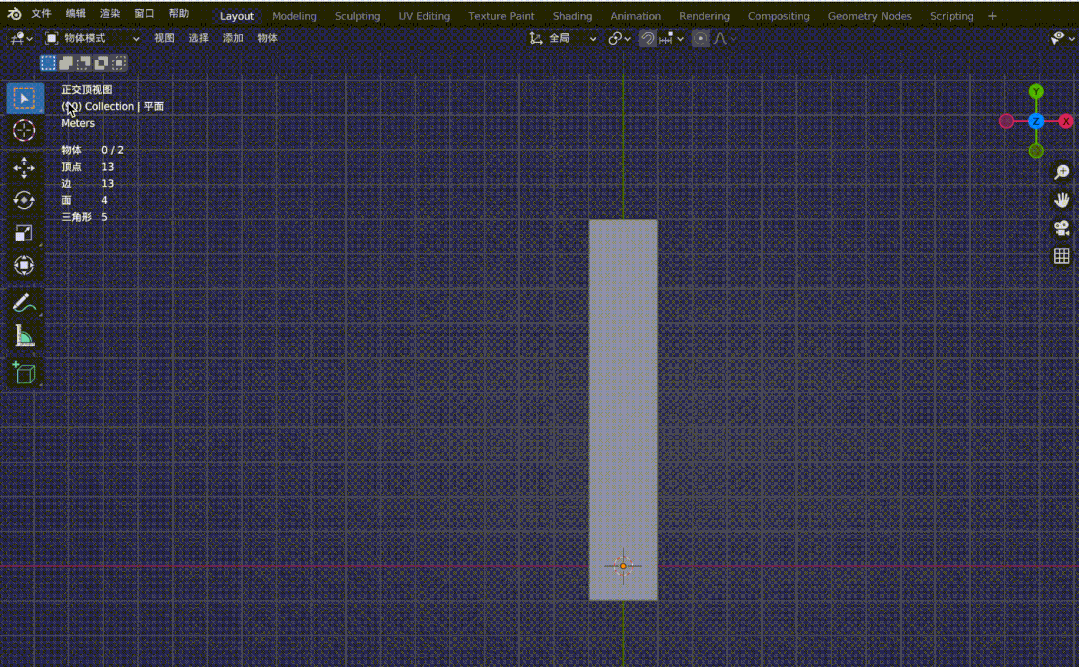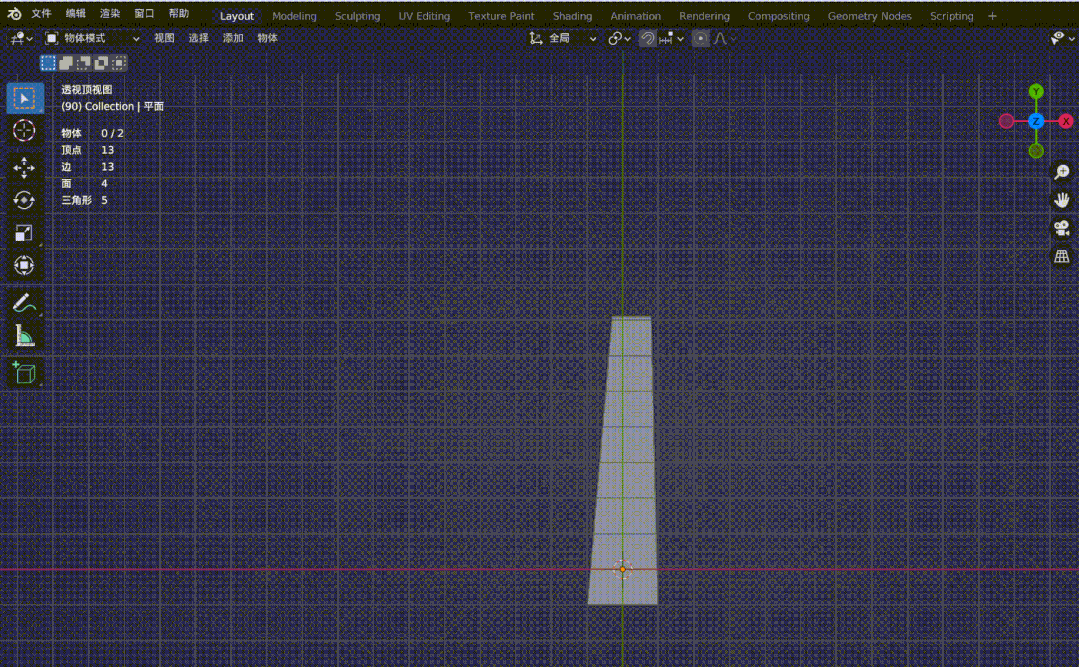
圖4-2
圖4-1鐵軌是平行的,但在透視投影的作用下,原本的平行線在遠處變得相交。圖4-2是觀察正交視圖和透視視圖來對比兩者區別,同樣,在透視投影下,會有近大遠小的效果,(圖中四個頂點坐標分別為(-1, 10, -20), (1, 10, -20), (-1, -1, 0), (1, -1, 0),z 軸俯視觀察。
關于透視投影部分還有以下幾點說明:
這里沒有推導透視投影矩陣,而是直接給出了矩陣變換后的效果圖,一是希望讀者從直觀上感受透視投影的效果,二是文章主要內容是光柵化過程的概述,推導不作為重點。如果想了解透視投影的原理,可以學習《GAMES101》或者從《Fundamentals of Computer Graphics》中尋找答案
針對透視投影的效果,最終呈現出來的就是近大遠小的視覺效果
無論是正交投影還是透視投影,我們目前做的都是針對幾何圖形的變換,但是最終的目的是屏幕顯示,屏幕顯示必然涉及到分辨率和屏幕尺寸。所以,正交投影和透視投影的最后一步都是標準化(圖3-2),最終得到[-1, 1] ^ 3的標準立方體。屏幕上的窗口可以是動態變化的,如:400 x 600,600 x 800等,標準化后通過簡單平移 + 縮放即可完成視口變換。
結合我們的模型,對兩個三角形做透視投影(圖5-1),可以看到兩個三角形都在平截頭體中,做透視投影后(乘透視矩陣)會先得到標準立方體,然后向[x, y]平面投影(暫時忽略z),得到具有近大遠小效果的圖(圖5-2),圖5-2動態比對正交投影和透視投影差別,可以很明顯看到透視投影之后,z絕對值大的三角形會變小很多。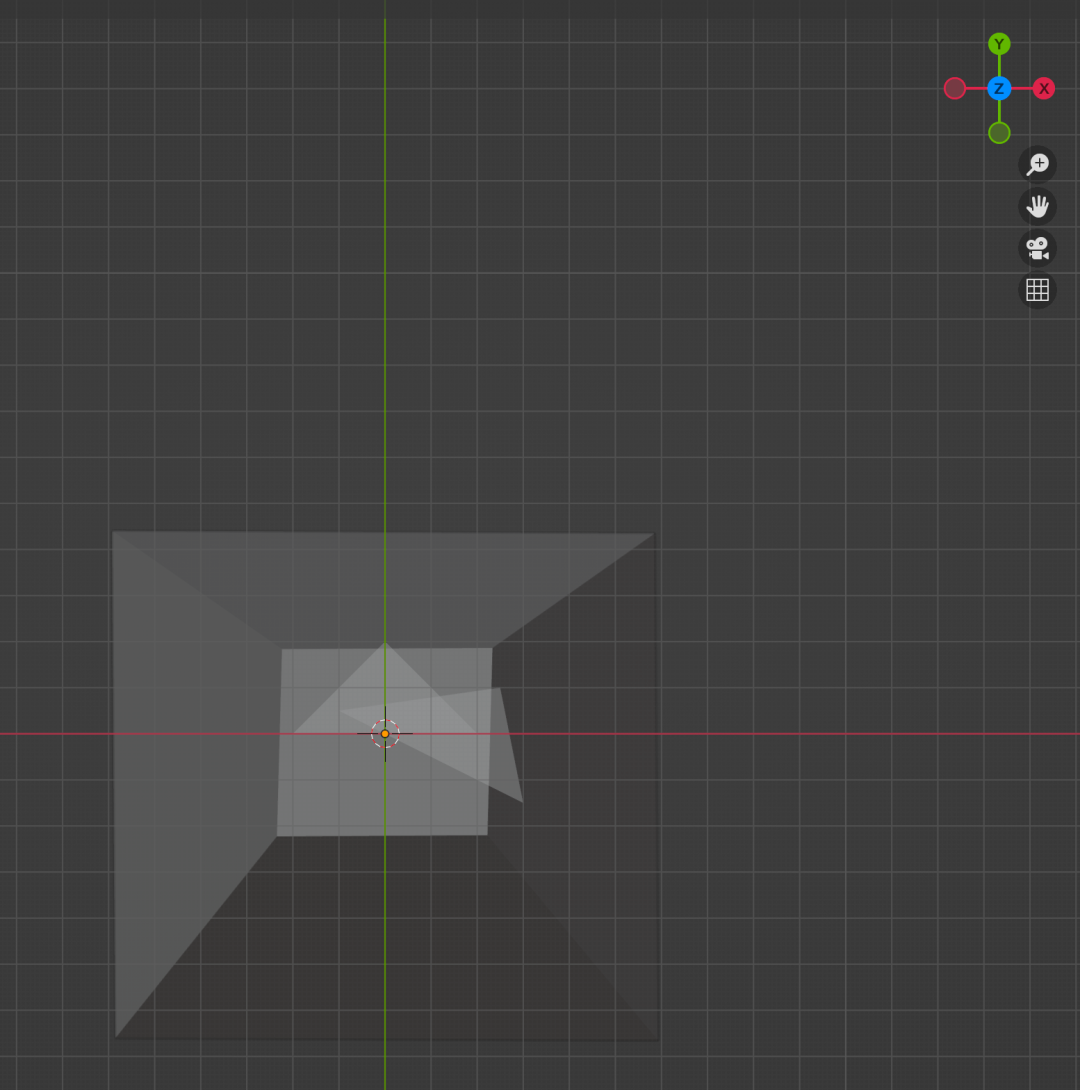
圖5-1 包含在平截頭體中的三角形

圖5-2 最終顯示的三角形(透明)
光柵化 & 著色
在透視投影之后,得到的是[-1, -1] ^ 3標準立方體,這一小節要講的是如何將這個標準立方體投影并繪制在屏幕上。具體過程如下圖所示。 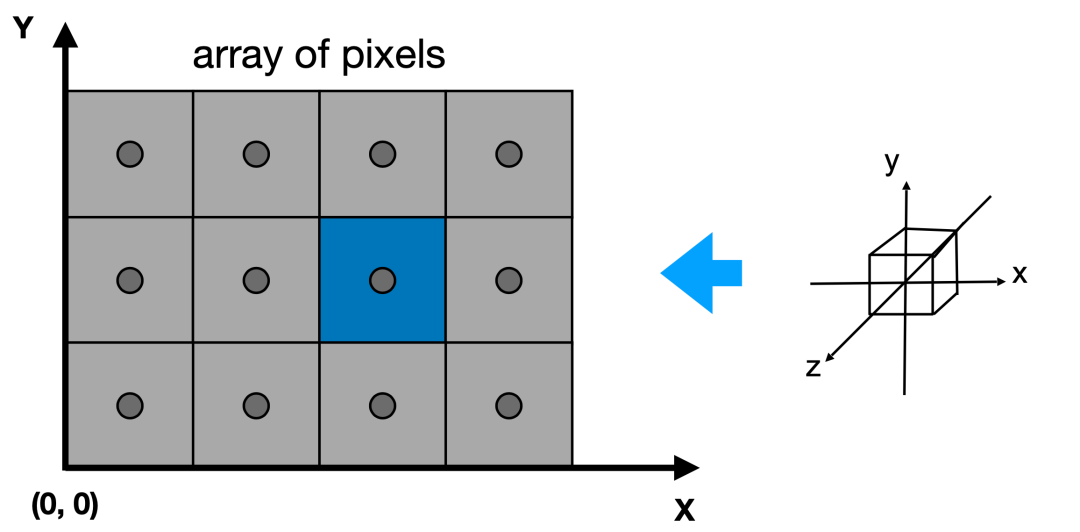
圖6-1
圖中有如下兩點需要注意:
這里先對屏幕做個簡單的抽象,將各個像素抽象為正方形,像素中心即為正方形中心,每個小格子就是一個像素,每個小方格子為 1 * 1,像素位于中心,坐標為(x + 0.5, y+0.5)
上一小節提到了透視投影之后,會標準化成 [-1, 1] ^ 3 的標準化立方體,這時先忽略 z 坐標,根據立方體中各個點的 [x, y] 坐標投在屏幕上。當前的[x, y]是標準化坐標,需要做個簡單的平移 + 縮放操作,將 x -> width,y -> height,其中 width、height 代表的屏幕中顯示窗口大小,這一步叫做視口變換。
回到我們開始的模型,兩個三角形,共有 6 個頂點,這里假設所有的圖形都不會被裁剪,我們假設三角形三個頂點在在經歷透視投影 --> 標準化 --> 視口變換后的坐標與屏幕坐標關系如下圖所示(這里是效果示意圖,并不是按照上文模型中的坐標得出): 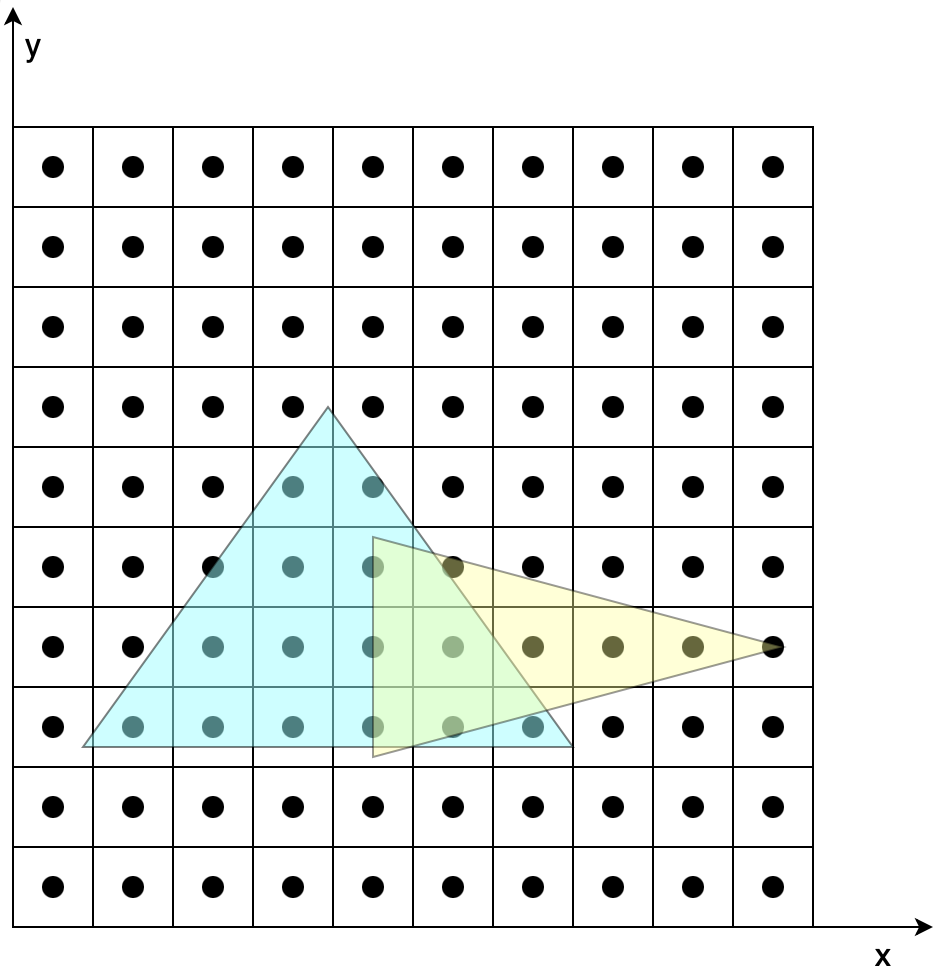
圖7-1 投影示意圖
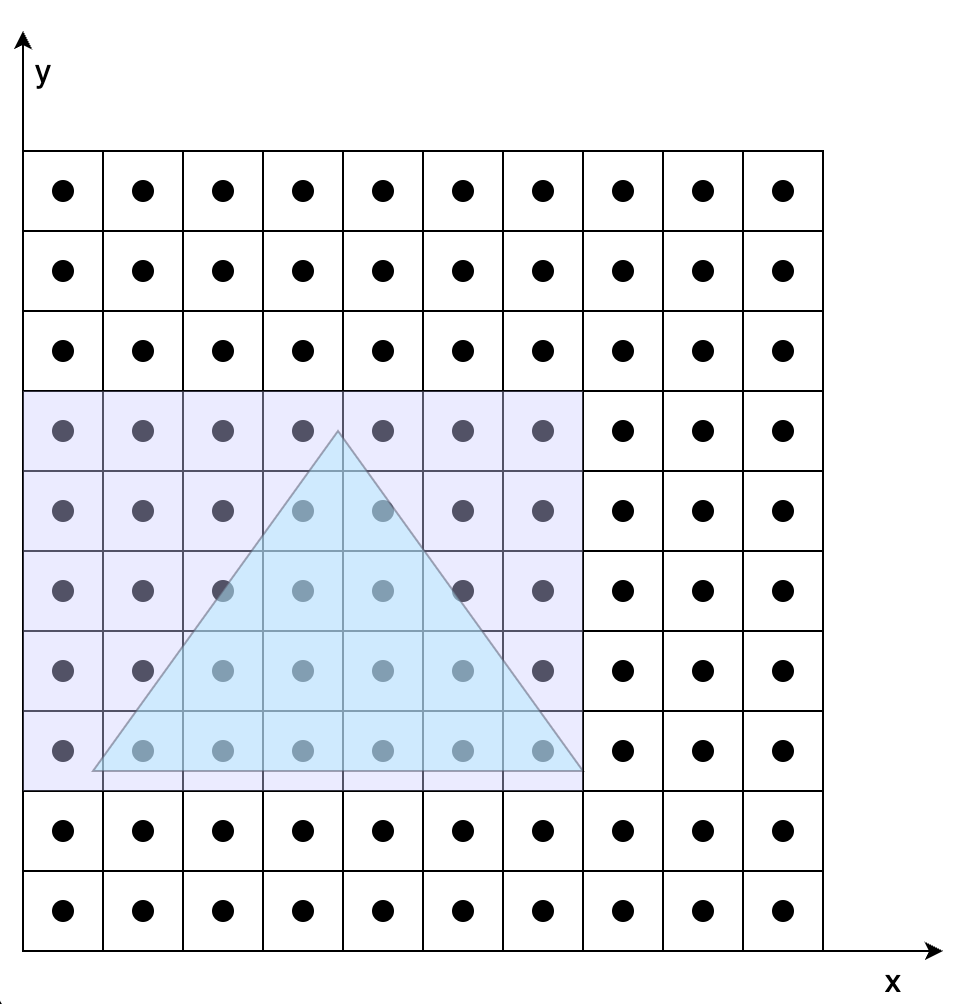
圖7-2 包圍盒光柵化
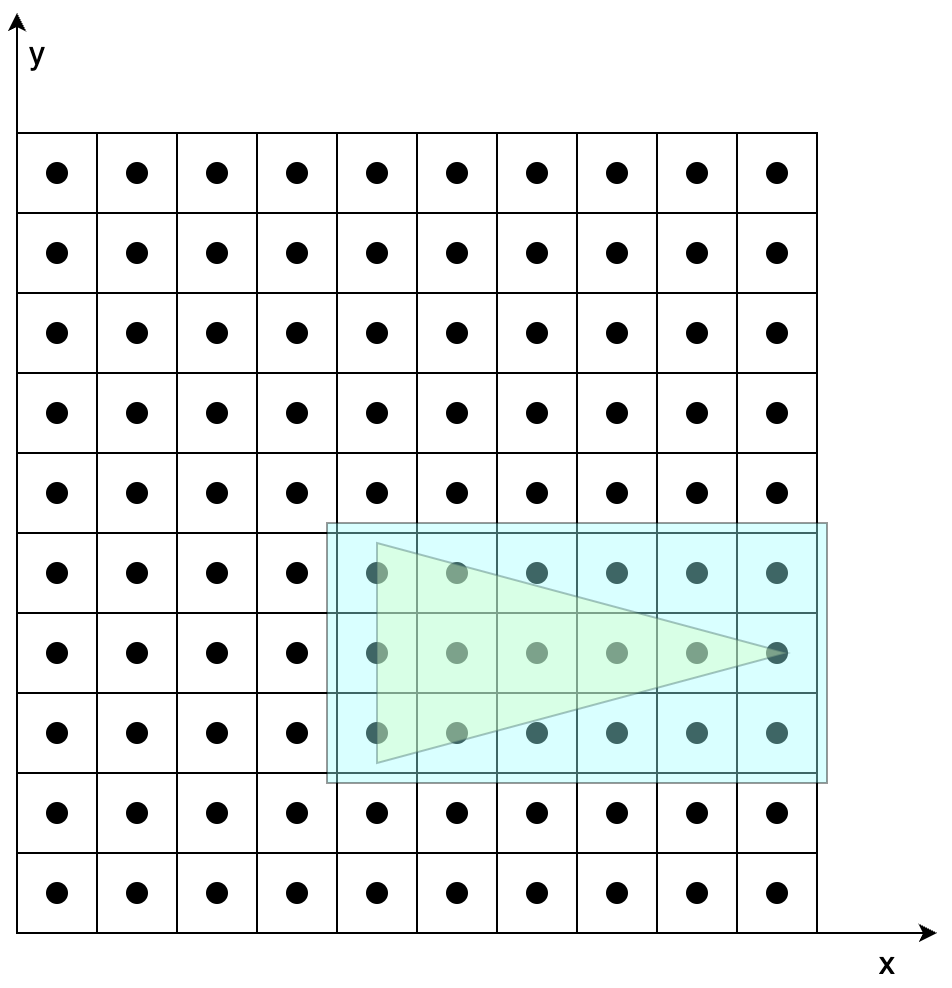
圖7-3 包圍盒光柵化
圖7-1在不考慮覆蓋的情況下,根據兩個三角形各自頂點變換后的結果,確定兩個三角形的位置。圖7-2、7-3是在確定三角形位置后,根據三角形覆蓋的像素對其著色。具體步驟如下(以圖7-2為例):
首先根據投影后三個頂點的范圍確定一個包圍盒,這么做的好處是減少搜索范圍。
確定了包圍盒后,依次判定包圍盒中的像素是否在三角形內,這里可以用向量叉乘方法,根據叉乘方向是否同向判定。
對于包含在三角形內的像素,對其進行著色。著色過程中,涉及到紋理坐標、法向量等要素的計算,圖7-2中我們知道投影之后的三個頂點坐標、紋理坐標、法向量,但是無法獲得三角形內任一點的這些數據,這時候就會用到三角形的重心坐標,利用重心坐標通過插值的方法獲得三角形內任一點的數據。比如已知三角形三個頂點的紋理坐標(u, v),想知道三角形內任一點的紋理坐標,就可以通過該點的重心坐標獲取,有一點需要切記,這里所說的重心坐標不是投影后的,而是在做透視投影之前的重心坐標,如果要用投影后的重心坐標,需要做修正。對于三角形內法向量計算也是相同道理。
不過上面的方法仍然存在兩個問題:
圖7-2、7-3考慮的都只針對自身三角形的光柵化,對于兩個三角形的重疊部分沒有考慮,后面講的深度緩沖會解決這個問題。
在判定像素與三角形位置關系時,我們判定的是小方格中心點與三角形關系,即使中心點不在三角形內,像素的小方格子仍然會被三角形覆蓋,那么小格子是標記為不亮、還是按照被覆蓋的面積來著色,這塊如果處理的不好很容易出現鋸齒,這里就需要反走樣技術,這里不再闡述。
深度緩沖
在透視投影之后得到一個標準正方體,在向 x、y 確定平面投影時會遇到這樣的情況,對于兩個不同頂點,x、y 相同,z 不同,這時候就要借助深度緩沖方法。不考慮透明效果,上述兩個頂點,誰距離攝像機近,后面的就會被遮擋。具體方法如下。 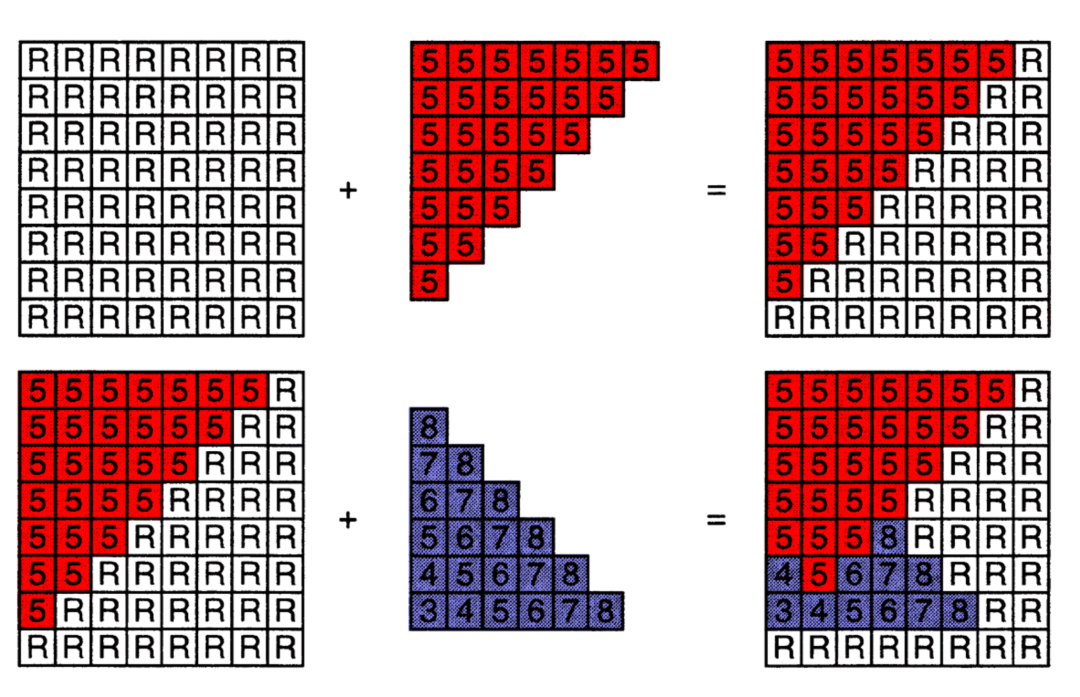
圖8-1 深度緩沖原理
在光柵化過程中,被著色的像素會記錄當前點在空間中距離攝像機深度,如果再次被著色的時候,會與之前記錄的深度值做比對,如果新的值距離攝像機更近,那么會覆蓋掉舊的顏色,否則仍然用舊的顏色。這樣就解決了點的覆蓋問題,上文僅僅是方法上的闡述,還有很多優化空間,比如我們可以提前深度值的判定,對于被覆蓋的點省掉不必要的著色操作。圖8-2是實例模型執行深度緩沖后的投影結果。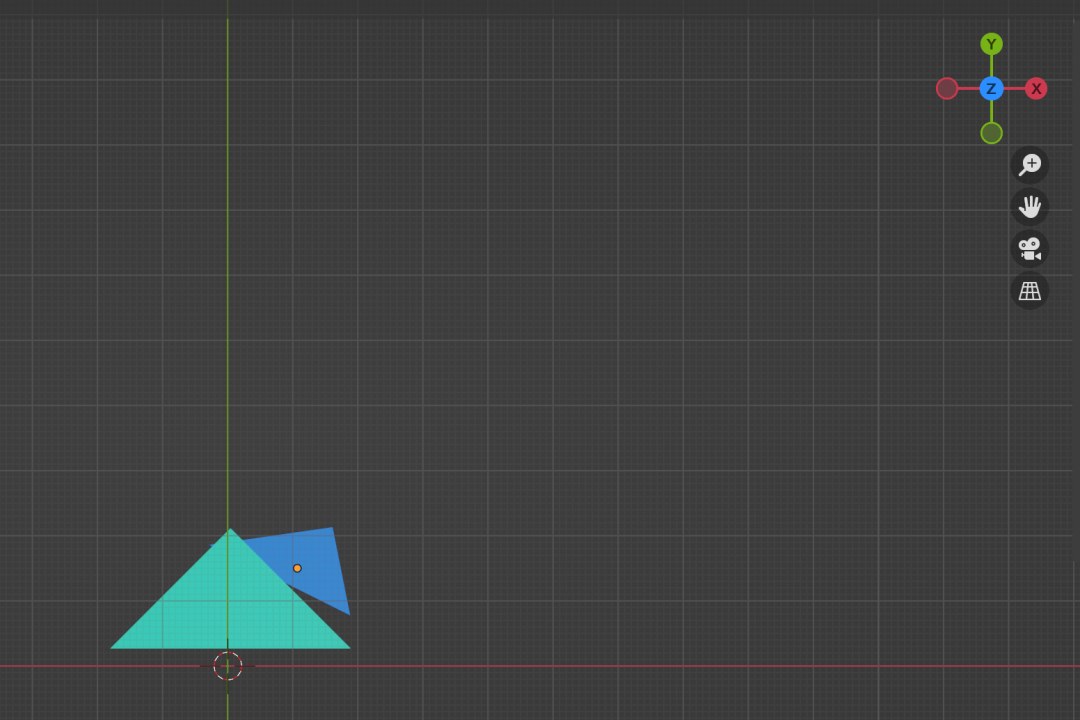
圖8-2 最終投影
總結
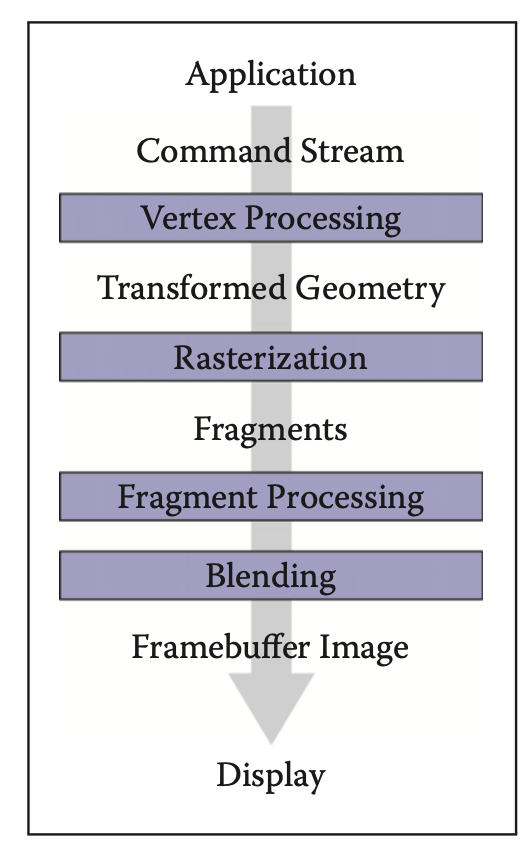
上圖是圖形管線的主要過程,對照上文例子中的簡單模型闡述各個環節工作:
Vertex Processing: 頂點處理,對空間中頂點進行變換,針對我們例子中簡化的兩個三角形模型,透視投影包含在頂點變換中。
Rasterization: 光柵化操作,對于我們這個例子就是對兩個三角形做透視投影 --> 然后向[x, y]平面做投影 --> 視口變換,然后判定投影后的三角形內包含了多少像素。
Fragment Processing: 像素著色,例子中就是針對投影后兩個三角形內的像素進行著色,這里與光照、紋理映射相關,對于三角形任一點的紋理坐標、法向量可以通過三角形頂點的這些信息及三角形重心坐標(透視投影前)計算得到。
Blending: 混合上屏,將最終混合結果填充到圖形緩沖區,進而刷到屏幕。
審核編輯:湯梓紅
-
光柵
+關注
關注
0文章
262瀏覽量
27365 -
3D
+關注
關注
9文章
2835瀏覽量
106991 -
gpu
+關注
關注
27文章
4588瀏覽量
128126 -
渲染
+關注
關注
0文章
68瀏覽量
10873 -
3d渲染
+關注
關注
0文章
8瀏覽量
12548
原文標題:3D渲染——光柵化渲染原理解析
文章出處:【微信號:OSC開源社區,微信公眾號:OSC開源社區】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
如何評價光柵化渲染中光線在場景中的折返?
渲染工具Luxion.Keyshot.v5.2.10
HDC2021技術分論壇:酷炫3D效果在瘦設備上也能實現?
缺少VGlite字體渲染api文檔,求分享
實時光線的混合渲染:光線追蹤VS光柵化
一種用機器學習進行3D實時渲染的新方法:用paGAN實現3D實時渲染
AMD與Pixelary合作,創造了3D渲染照片
NVIDIA Omniverse助力Epigraph輕松管理3D資產并加快渲染速度
VIVERSE 推行實時3D渲染: 探索Polygon Streaming技術力量與應用
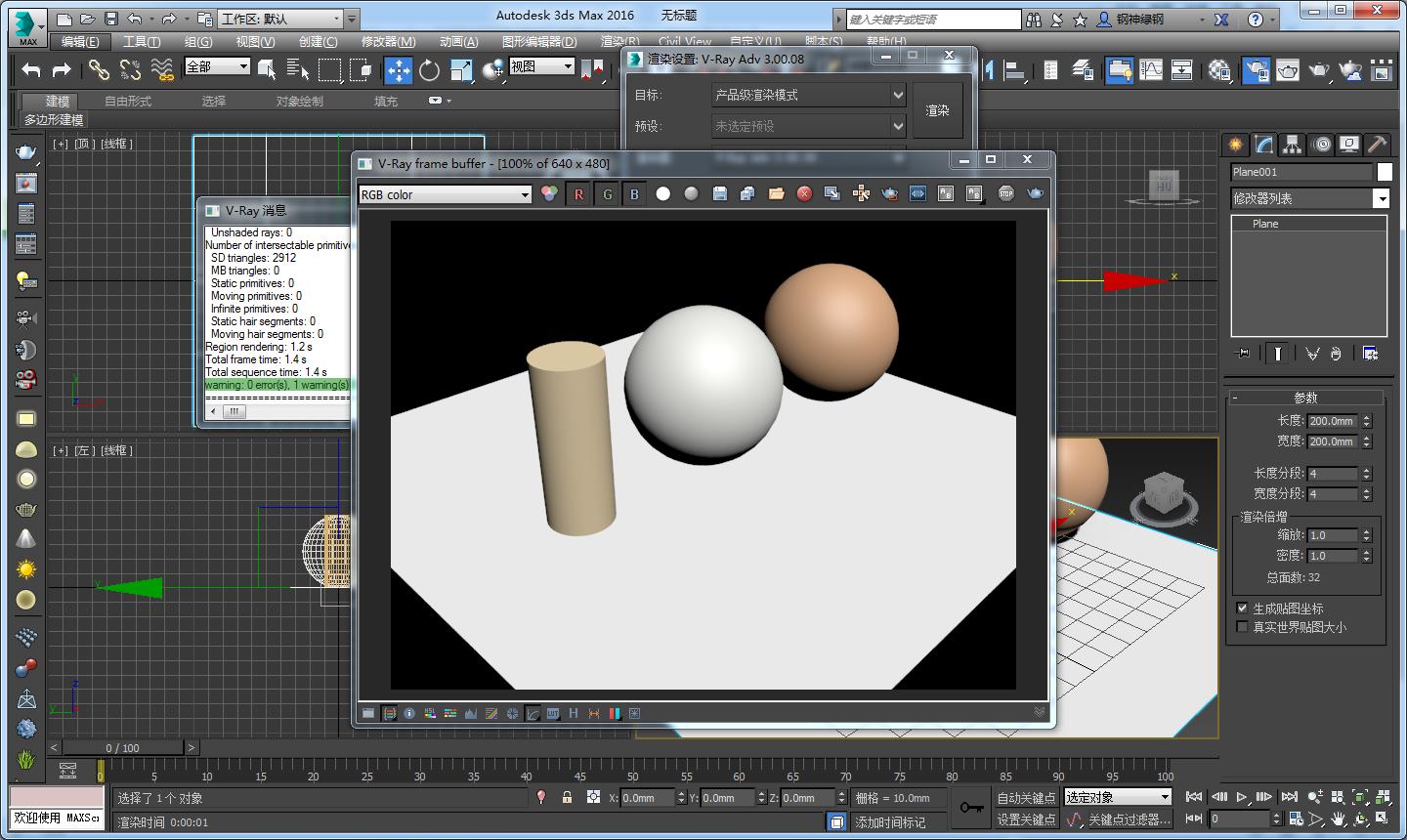




 3D渲染——光柵化渲染原理解析
3D渲染——光柵化渲染原理解析













評論