本文以常用汽車電驅動系統軸承為對象,首先分析了電驅動系統的結構特點,其次計算了電驅動系統中各傳動軸的扭矩、轉速以及軸承載荷;然后基于實際對象,運用MATLAB 語言,并采用Lundberg-Palmgren 模型計算了軸承疲勞壽命。最后采用疲勞損傷累積理論,計算分析了某電驅動系統軸承損傷,為電驅動系統的進一步研究提供可靠基礎。
1 電驅動系統結構
常用汽車電驅動系統為“電機軸-輸入軸-中間軸-輸出軸”結構。工作中,電驅動系統以電機軸的轉速和扭矩信號作為輸入,再經過總成中減速器的輸入軸、中間軸以及輸出軸各軸的斜齒輪,降低轉速增加扭矩,再通過輸出軸輸出。本文假設電機軸轉速順時針方向為正,即以前進擋位分析,其結構如圖1 所示。
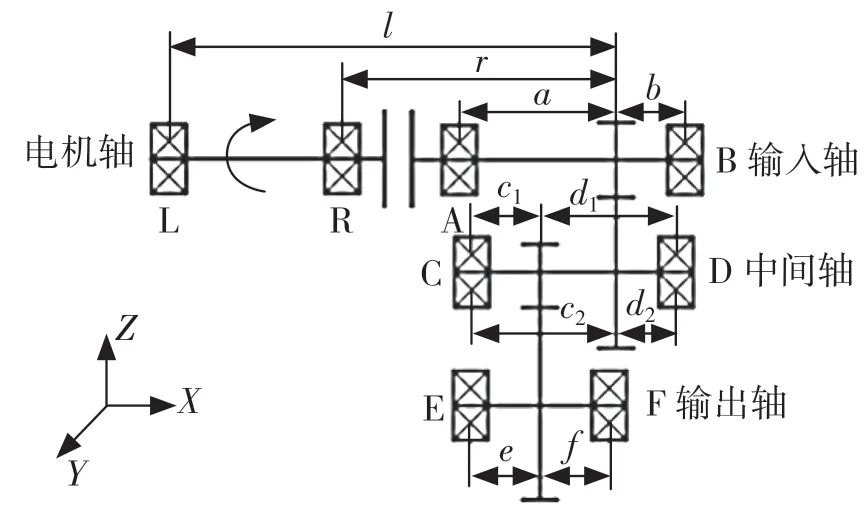
圖1 汽車電驅動系統軸系結構簡圖
Fig.1 Structure diagram of shaft system of automobile electric drive system
圖1 中,L 和R、A 和B、C 和D 以及E 和F分別表示電機軸、輸入軸、中間軸以及輸出軸上的左右端軸承,各軸承固定形式均為單向固定;l、r、a、b、c1、d1、c2、d2、e和f分別表示軸承與所在軸斜齒輪間的距離。
如圖2 所示,軸系中各傳動軸在空間上并不處于同一平面,這使得中間軸分別受到輸入軸和輸出軸斜齒輪兩者的徑向力不在同一方向上,所以在受力分解中間軸軸承的載荷時,需要首先考慮軸系各軸間的空間位置關系[3]。圖2 中軸系空間位置角θ的表達式為
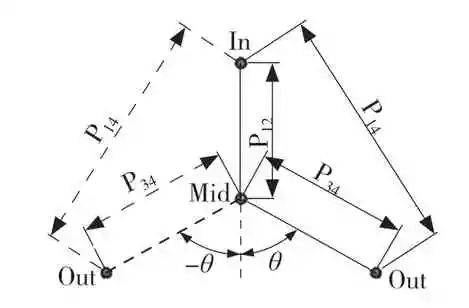
圖2 汽車電驅動系統軸系空間位置簡圖
Fig.2 Spatial position diagram of shaft system of automobile electric drive system
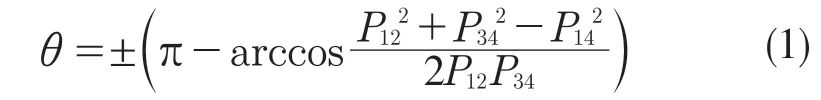
式中:P12,P14,P34——輸入軸和中間軸、輸入軸和輸出軸以及中間軸和輸出軸之間的空間距離。
2 軸承載荷計算 2.1 斜齒輪載荷計算
由于存在齒數比,軸承載荷計算需首先計算各個工況(軸上扭矩T、電機輸出轉速n)下斜齒輪的受力,才能進行載荷分配至軸承端。
斜齒輪圓周力Ft計算公式為

斜齒輪徑向力Fr計算公式為
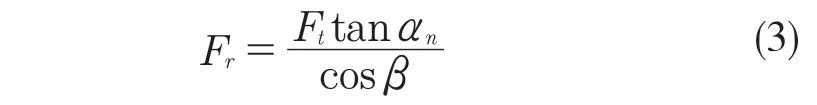
斜齒輪軸向力Fα計算公式為
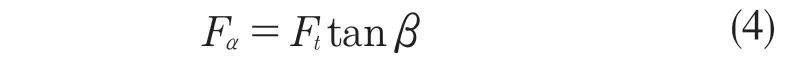
式中:T——該斜齒輪所在軸的扭矩,N·m;αn,d,β——斜齒輪壓力角、節圓直徑、螺旋角。
2.2 軸承載荷計算
2.2.1 電機軸軸承載荷計算
由于電驅動系統電機軸與輸入軸常以聯軸器相連,所以電機軸軸上扭矩為T,轉速為n。忽略軸的撓曲對齒輪和軸承載荷的作用,電機軸軸承載荷主要考慮減速器輸入軸斜齒輪所受扭矩作用,其軸承徑向力由斜齒輪所受圓周力和徑向力綜合而成。由于連軸器的緩沖功能,認為電機軸上的兩端軸承均不承受軸向力。電機軸軸承載荷如表1 所示。
表1 電機軸軸承載荷
Tab.1 Motor shaft bearing load

2.2.2 減速器軸系軸承載荷計算
由于齒數比,轉速由電機軸傳至輸出軸會依次遞增,而扭矩依次遞增,各軸扭矩與轉速如表2所示。基于力的平衡關系,可求出如表3 所示的減速器各傳動軸軸承端所受載荷。
表2 減速器各傳動軸扭矩轉速
Tab.2 Torque and speed of each drive shaft of the reducer

表3 減速器各傳動軸軸承載荷
Tab.3 Bearing load of each drive shaft of the reducer

其中,±或?當T>0 時取上面符號,當T≤0 時取下面符號;{Ft;Fr;Fa}和{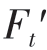 ;
;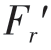 ;
;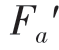 }分別表示斜齒輪1、2 和斜齒輪3、4 間的圓周力、徑向力及軸向力;zx表示斜齒輪x的齒數。
}分別表示斜齒輪1、2 和斜齒輪3、4 間的圓周力、徑向力及軸向力;zx表示斜齒輪x的齒數。
3 軸承疲勞壽命與損傷計算 3.1 軸承疲勞壽命計算
根據Lundberg-Palmgren 壽命理論[4,5],軸承疲勞壽命的基本計算公式為
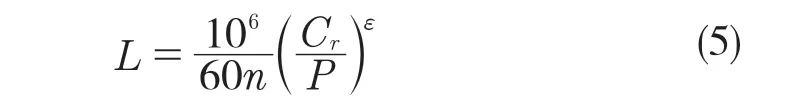
式中:C——徑向基本額定動載荷;P——當量動載荷;ε——壽命指數,球軸承取3,滾子軸承取10/3。
軸承基本額定動載荷Cr以及當量動載荷P為
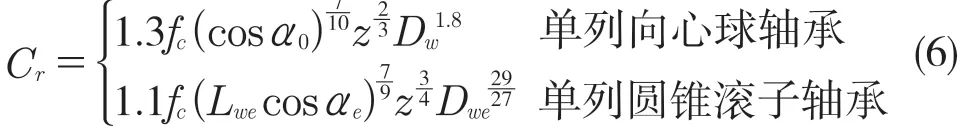
式中:fc——和軸承結構有關的修正系數[6];α0——球軸承接觸角;αe——圓錐滾子軸承錐度角;z——滾動體數量;Dw——球軸承滾珠直徑;Dwe——圓錐滾子軸承滾子等效直徑;Lwe——滾子有效接觸長度。
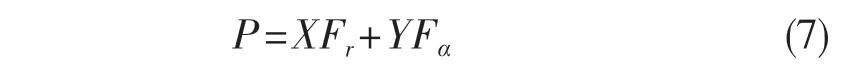
式中:X——徑向動載荷系數;Y——軸向動載荷系數[6]。
3.2 軸承損傷計算
軸承疲勞失效為典型的損傷累積過程,在許多應用場合中,軸承承受隨時間變化的循環載荷,而不是固定載荷,對于這類工況,可采用Palmgren-Miner 線性累計損傷法則[7,8]。
軸承在當量動載荷為P1的運轉條件下,滾道的壽命L1,若在此工況下運轉了N1轉,則P1的運轉條件下軸承的當量損傷為: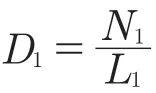 。若軸承經歷一段隨機道路載荷,依次在P1,P2,…?,Pn當量負荷作用下運轉了N1,N2,…?,Nn轉,則該隨機道路載荷對軸承造成的損傷為:
。若軸承經歷一段隨機道路載荷,依次在P1,P2,…?,Pn當量負荷作用下運轉了N1,N2,…?,Nn轉,則該隨機道路載荷對軸承造成的損傷為:
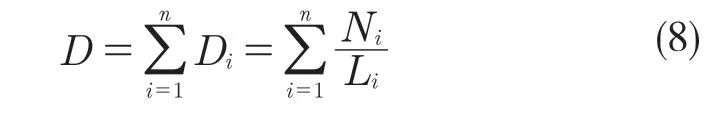
其中,n為軸承的一組運轉條件,對應的每一種運轉條件i,軸承所對應的疲勞壽命為Li轉,但在此工作條件下軸承只運轉了Ni轉,Ni
4 實例分析
以某汽車電驅動系統總成為例,其軸系參數及軸承結構參數分別如表4 和表5 所示。
表4 電驅動系統軸系參數
表5 電驅動系統軸承結構參數
以圖3 和圖4 所示的實驗場電機軸扭矩-轉速載荷譜作為輸入,將每1 s 作為一個穩態工況,即單個穩態工況下該軸承的損傷為
圖3 電驅動系統電機軸轉速載荷譜
圖4 電驅動系統電機軸扭矩載荷譜
式中:n——該軸承所在軸的轉速。
然后根據本文的計算方法,運用MATLAB 語言求解計算,各軸承損傷結果如圖5 所示。
圖5 電驅動系統軸承損傷計算結果
可以看出,軸承R、E 和F,即電機軸右端軸承和輸出軸左右端軸承的損傷明顯大于其他軸承。原因可能是電機軸承載的轉速最高,且電機軸右端載荷比左端更大;而輸出軸兩端軸承雖然轉速較低,但是承受載荷較大導致損傷較高,結果符合工況真實情況。
5 結論
本文總結了電驅動系統各傳動軸軸承載荷工況的計算方法,且考慮到了軸系結構、空間位置的影響,具有較好的實用性和通用性,能夠為電驅動系統軸承工況研究提供參考。
基于試驗場載荷,結合L-P 和Miner 理論,計算了電驅動系統各傳動軸軸承的疲勞壽命以及損傷。該方法充分考慮到汽車電驅動系統載荷譜的高隨機性特點,能夠為汽車電驅動系統軸承的選型、軸系結構優化等提供幫助。
本文未考慮軸承實際運行中會承受傾覆力矩,該力矩對軸承疲勞壽命有一定影響,因此對于電驅動系統軸承損傷的計算分析有待進一步研究。
Tab.4 Electric drive system shafting parameters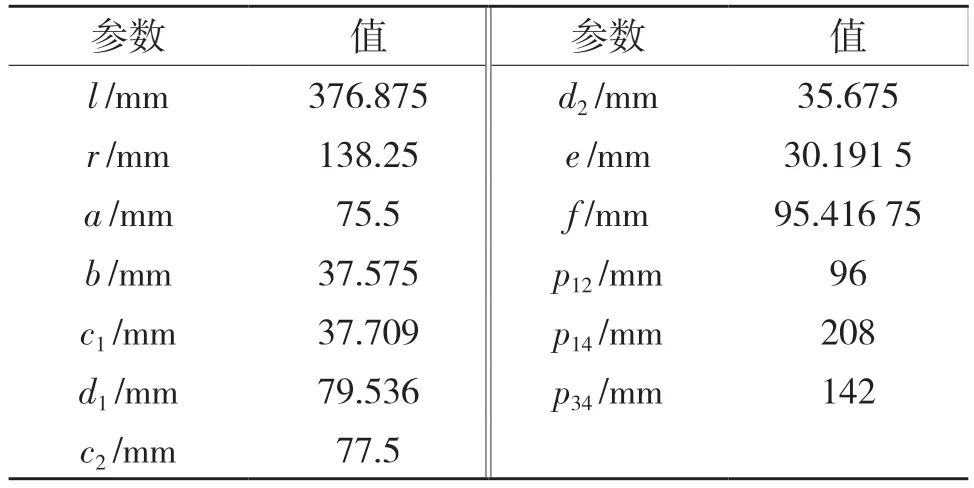
Tab.5 Electric drive system bearing structure parameters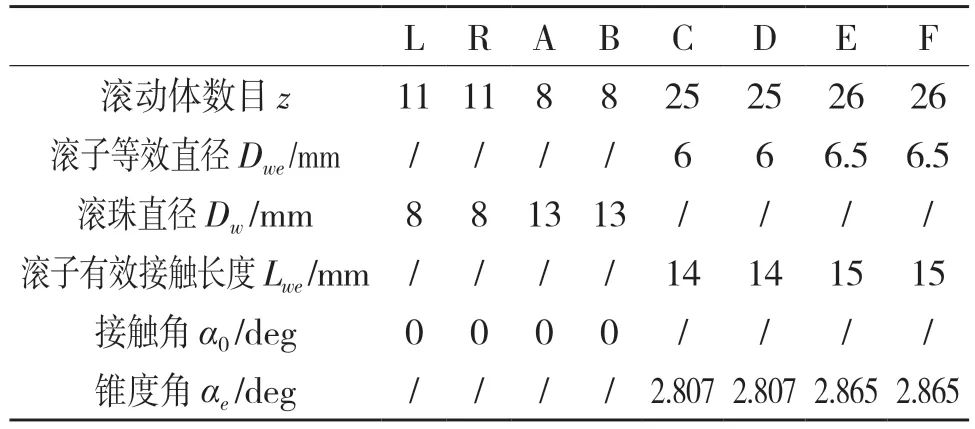
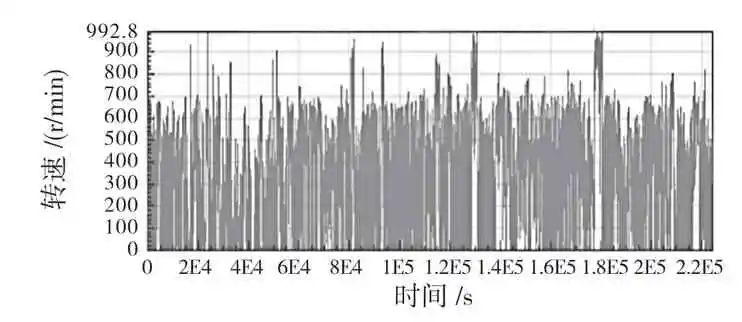
Fig.3 Motor shaft speed load spectrum of electric drive system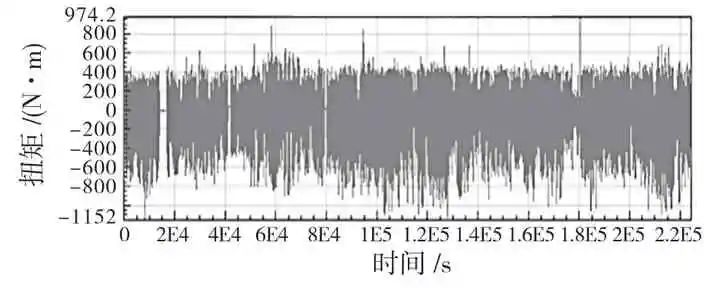
Fig.4 Torque load spectrum of electric drive system motor shaft
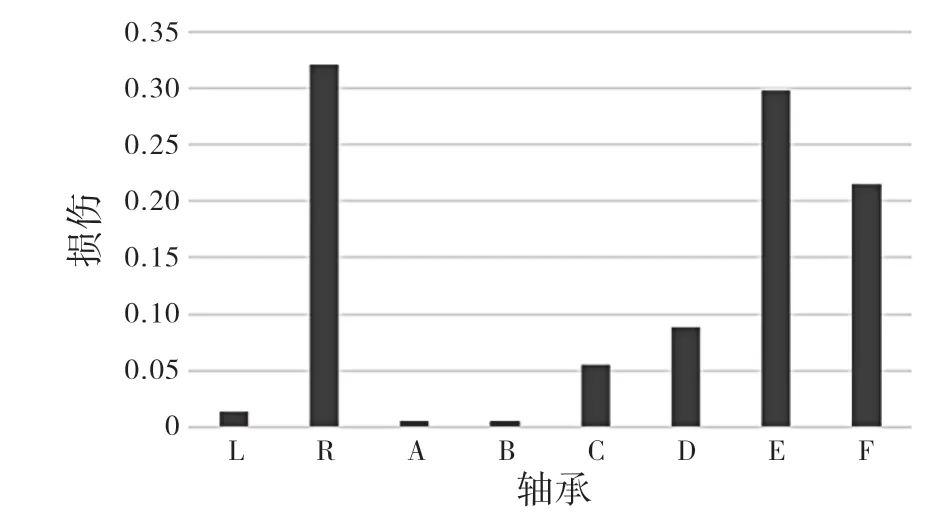
Fig.5 Calculation results of bearing damage of electric drive system
-
matlab
+關注
關注
182文章
2963瀏覽量
230149 -
扭矩
+關注
關注
1文章
63瀏覽量
12644 -
電驅動
+關注
關注
1文章
113瀏覽量
12256
原文標題:電驅動系統軸承損傷計算分析
文章出處:【微信號:EDC電驅未來,微信公眾號:EDC電驅未來】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 電驅動系統各傳動軸軸承載荷工況的計算方法
電驅動系統各傳動軸軸承載荷工況的計算方法










評論