前言
本章節首先介紹SVPWM控制技術的原理,然后詳細分析SVPWM控制算法的具體實現方式包括7段式SVPWM與5段式SVPWM算法,并通過Matlab/Simulink對SVPWM控制算法進行仿真分析,最后通過永磁同步電機矢量控制的實例進行算法應用。
一、SVPWM的控制原理
SPWM控制技術主要控制逆變器的輸出電壓盡量接近正弦波,并未顧及輸出電流的波形。 電流滯環跟蹤控制則直接控制輸出電流接近正弦波。
交流電機需要輸入三相正弦電流的最終目的是在電機空間形成圓形旋轉磁場,從而產生恒定的電磁轉矩。 把逆變器和交流電機視為一體,以圓形旋轉磁場為目標來控制逆變器的工作,這種控制方法稱做“磁鏈跟蹤控制”,磁鏈軌跡的控制是通過交替使用不同的電壓空間矢量實現的,所以又稱為“電壓空間矢量PWM(Space Vector PWM,SVPWM)控制”。
實踐和理論證明,與直接的 SPWM 技術相比,SVPWM 算法的主要優點有:
1、SVPWM優化諧波程度比較高,消除諧波效果要比SPWM好,容易實現,并且可以提高電壓利用率,輸出電壓最高可提高15%左右。
2、SVPWM算法提高了電壓源逆變器的直流電壓利用率和電機的動態響應速度,同時減小了電機的轉矩脈動等缺點。
3、SVPWM比較適合于數字化控制系統。
二、空間矢量的概念
在三相逆變器控制中,通常輸入輸出三相變量要分別描述,若能將三相變量用一個合成量表示,并保持信息的完整性,則三相的問題將簡化為單向的問題,由此引入空間矢量的概念。

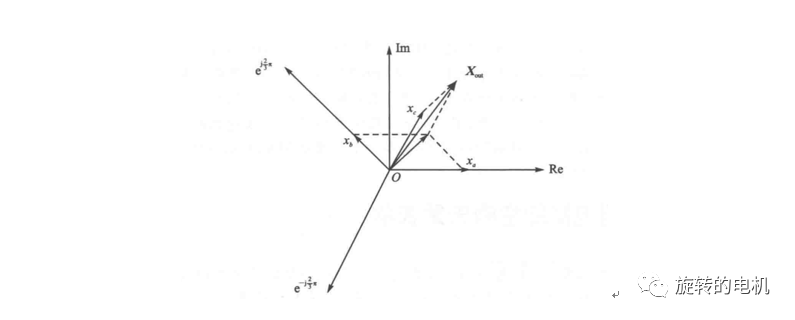



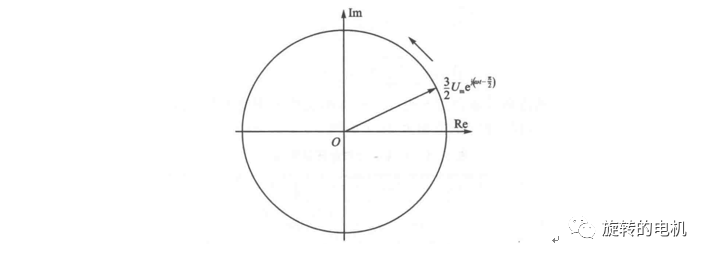
三、電壓與磁鏈空間矢量的關系



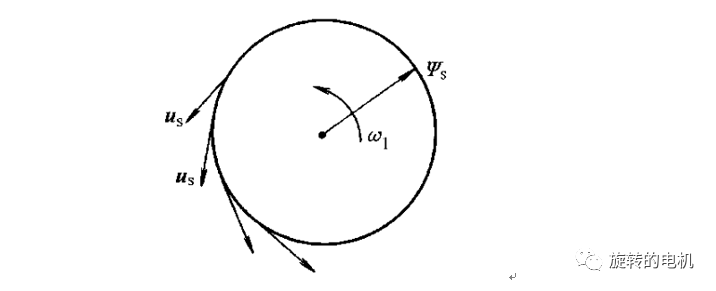
四、三相逆變器的基本電壓空間矢量
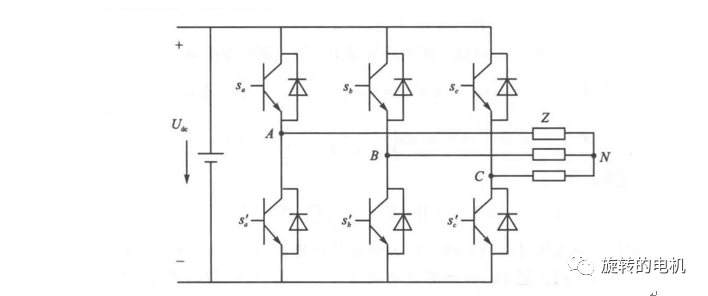

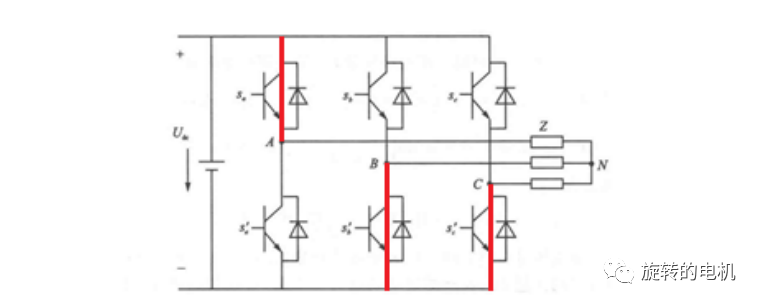
此時上圖的等效電路為:
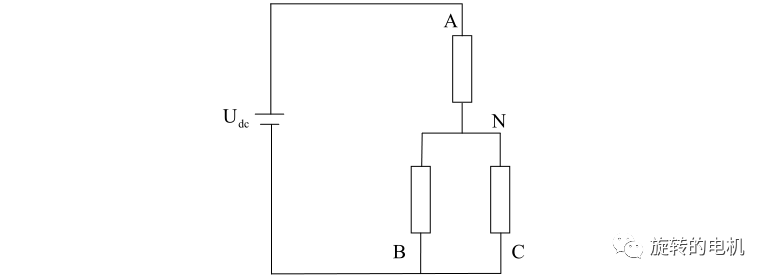
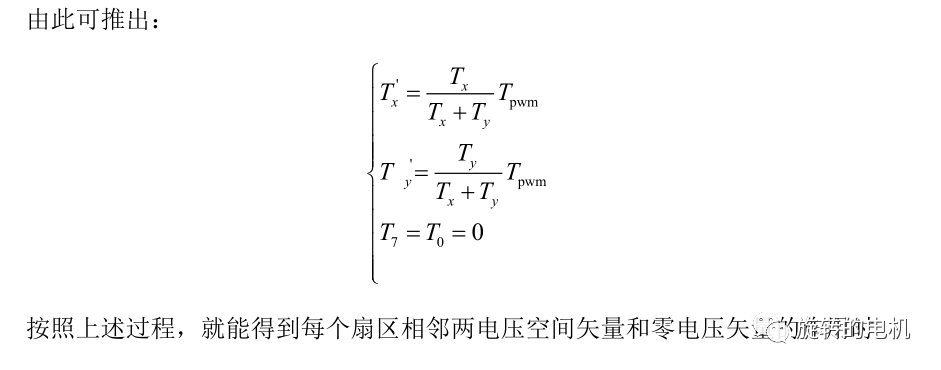
由此可推出:
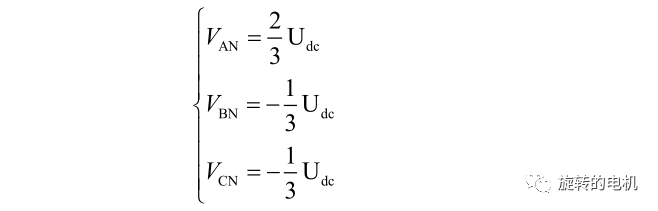
同理,可推出其他組合的電壓空間矢量如下表所示:
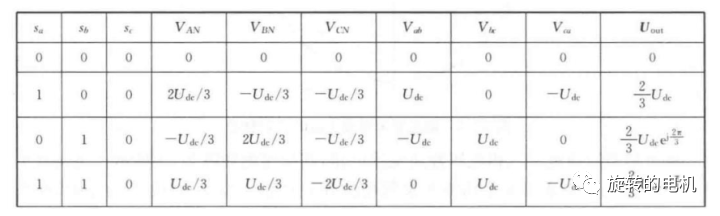
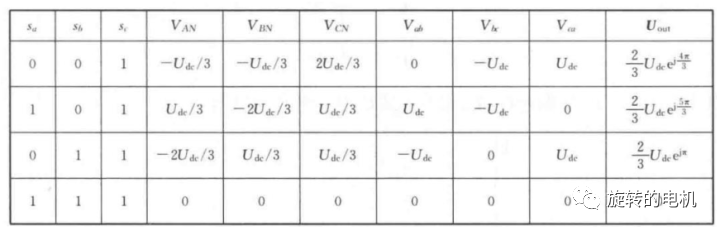

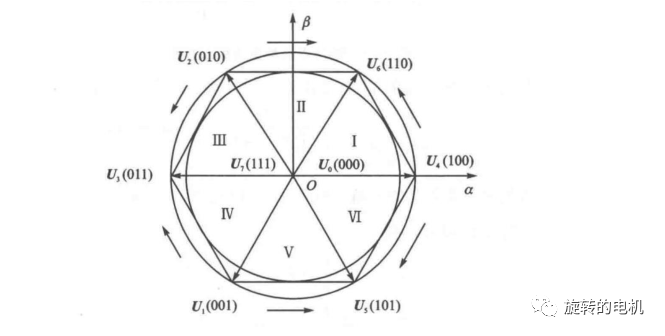
五、SVPWM 算法的合成原理


由上述分析三相正弦波電壓在電壓空間向量中合成一個等效的旋轉電壓矢量,其旋轉速度為輸入的電源角頻率,該等效旋轉電壓矢量的運動軌跡為圓形。所以要產生三相正弦波電壓,可以利用以上電壓空間矢量合成的技術,在電壓空間向量上,將設定的電壓向量由一起始位置開始如 100,每次增加一個小增量,每個小增量設定的電壓向量可以用該區中相鄰的兩個基本非零向量與零電壓矢量予以合成,如此所得到的設定電壓向量就等效為一個在電壓空間向量平面上平滑旋轉的電壓空間矢量,從而達到電壓空間矢量脈寬調制的目的。
六、SVPWM 算法推導

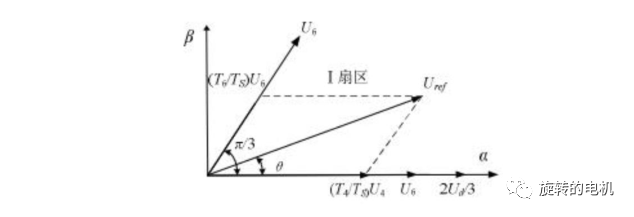




一個開關周期中空間矢量按分時發生作用,在時間上構成一個空間矢量的序列,空間矢量的序列組織方式有多種,按照空間矢量的對稱性分類,可分為兩相開關換流和三相開關換流。
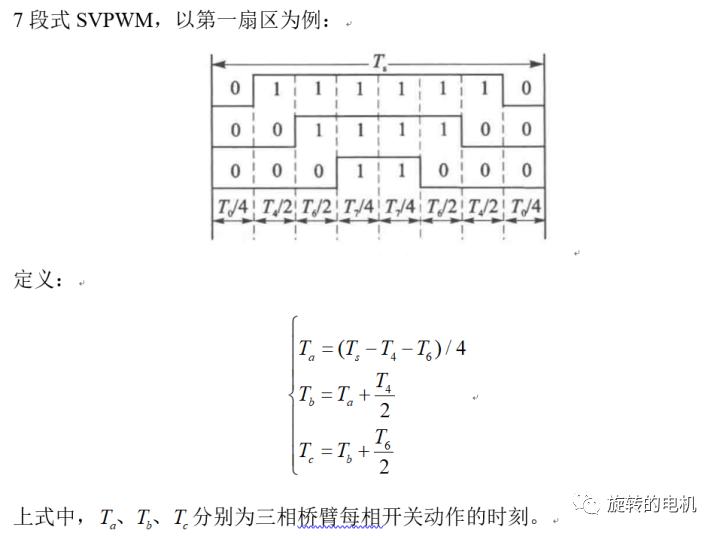
6.1.七段式SVPWM
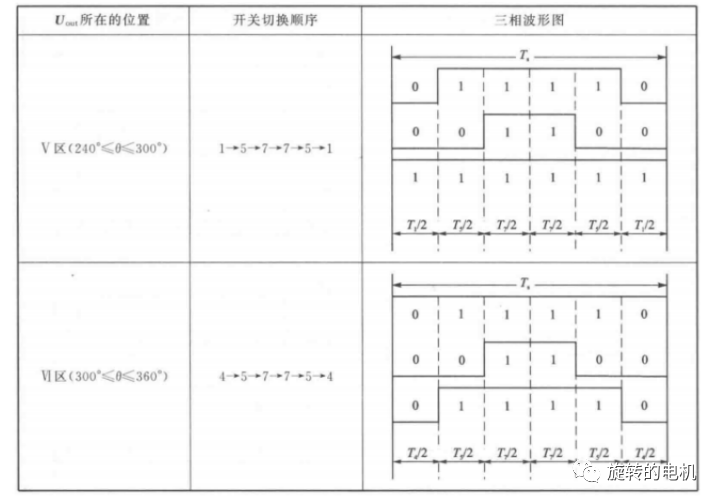
以減少開關次數為目標,將基本矢量作用順序的原則選定為:在每次開關狀態轉換時,只改變其中一相的開關狀態。并且對零矢量在時間上進行了平均分配,以使產生的 PWM 對稱,從而有效的降低 PWM 的諧波分量。例如當從100變為 000 時只需要改變 A 相橋臂上下開關管的狀態,當從 100 變為 111 則需要改變 BC 兩相橋臂上下開關管的狀態,這種方式增加了一倍的開關損耗。因此,要改變電壓向量 100、010、001 的大小需配合零電壓矢量 000,要改變110、011、101 的大小需配合零電壓矢量 111。這樣通過在不同區間內安排不同的開關切換順序,就可以獲得對稱的輸出波形,其他各扇區的開關順序如下所示:
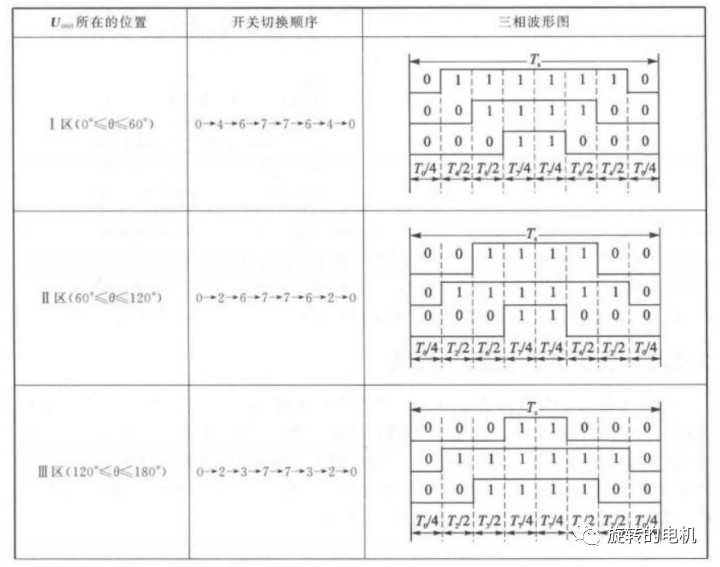
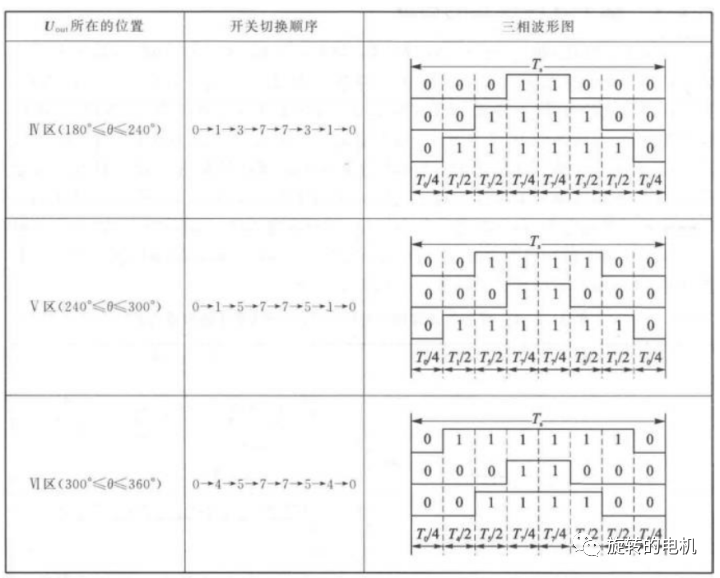

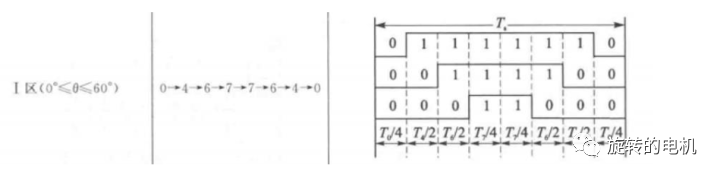
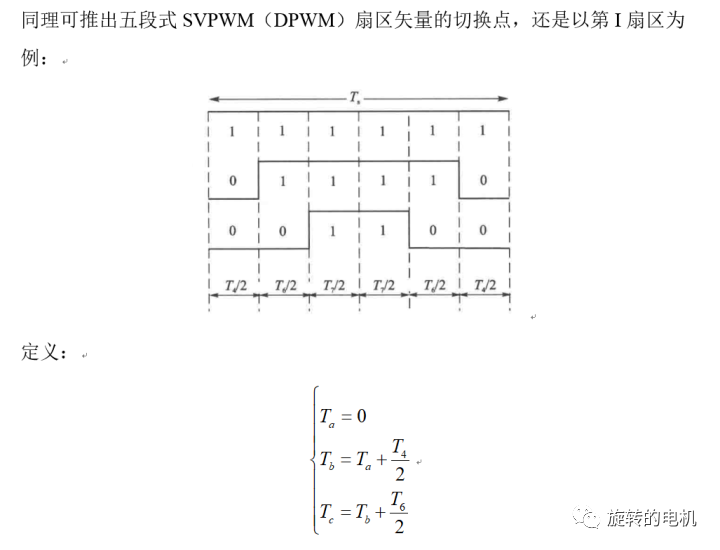
6.2.五段式SVPWM(又稱DPWM)
對 7 段式 SVPWM 而言,發波對稱,諧波含量較小,但是在每個開關周期Ts內有 6 次開關切換。為了進一步減少開關次數,采用每相開關在每個扇區狀態維持不變的序列安排,即5段式SVPWM,使得每個開關周期只有 3 次開關切換,但5段式SVPWM會增大諧波含量,如下表所示:
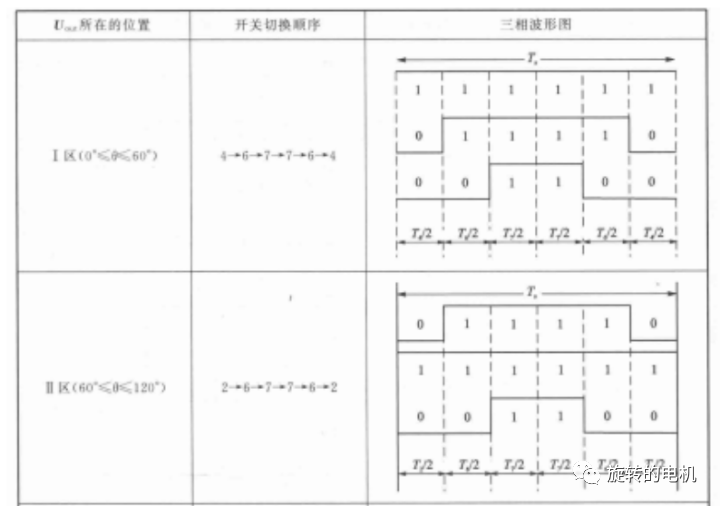
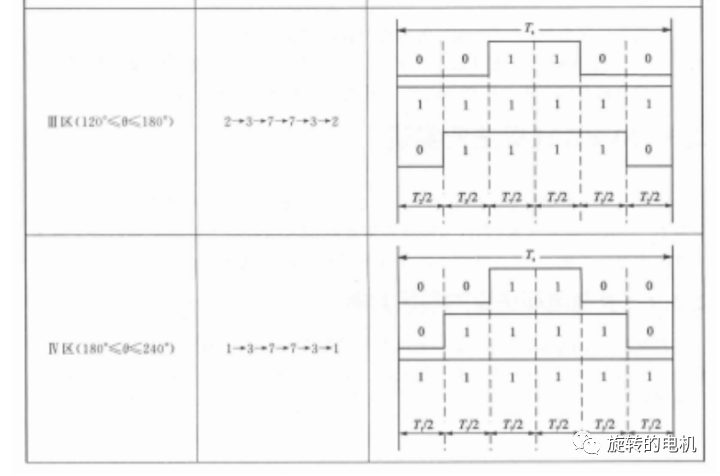
七、SVPWM 算法實現

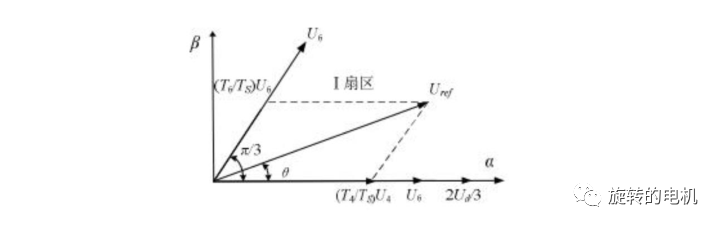

7.1.合成矢量Uref所處扇區的判斷






7.2.基本電壓空間矢量作用時間計算
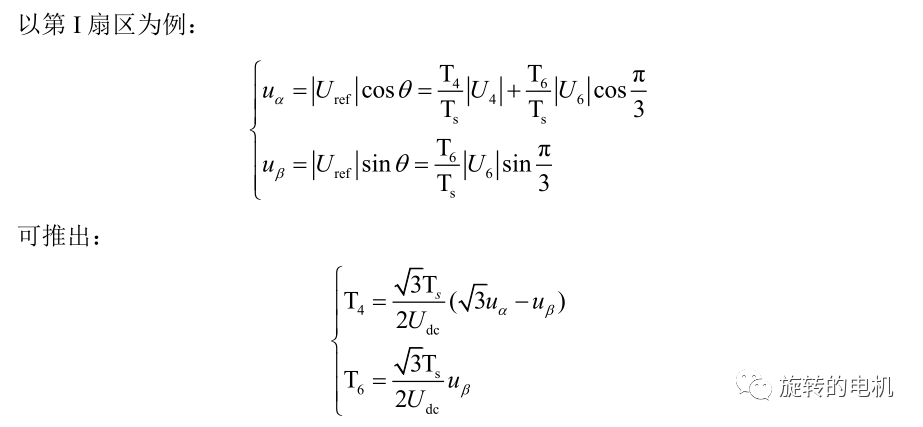


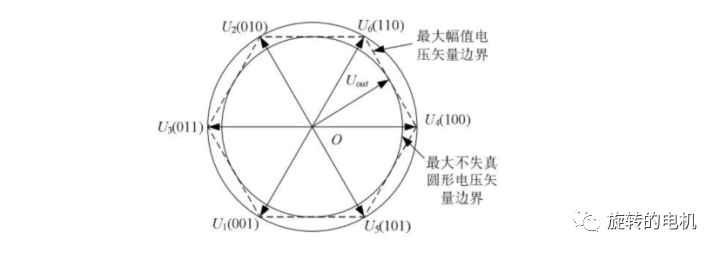
當兩個零矢量作用時間為 0 時,一個 PWM 周期內非零電壓矢量的作用時間最長,此時的合成空間電壓矢量幅值最大。 從下圖可知其最大幅值不會超過圖中所示的正六邊形邊界,而當合成矢量落在該邊界之外時,將發生過調制,逆變器輸出電壓波形將發生失真。 在 SVPWM 調制模式下,逆變器能夠輸出的最大不失真圓型旋轉電壓矢量為下圖所示虛線正六邊形的內切圓,其幅值為:



7.3.扇區矢量切換點的確定
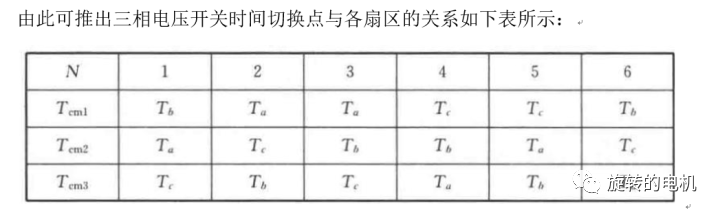
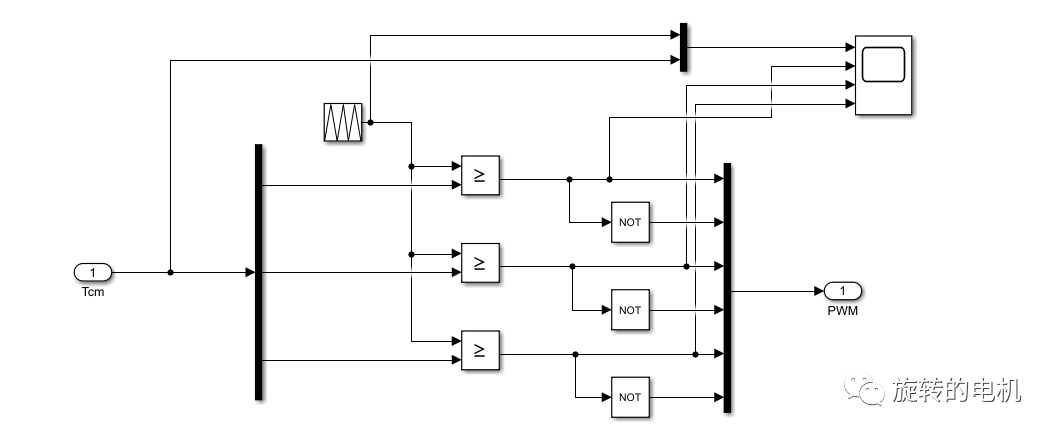
7.4.PWM信號生成
扇區矢量切換點確定后,用一定頻率的三角載波信號與各個扇區矢量切換點進行比較,從而產生逆變器所需的PWM控制信號。
八、七段式SVPWM仿真分析
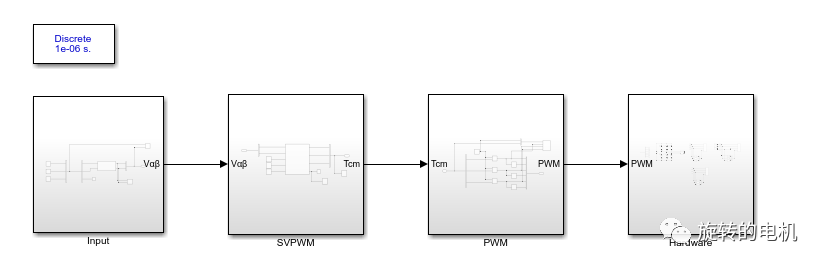
8.1.仿真電路分析
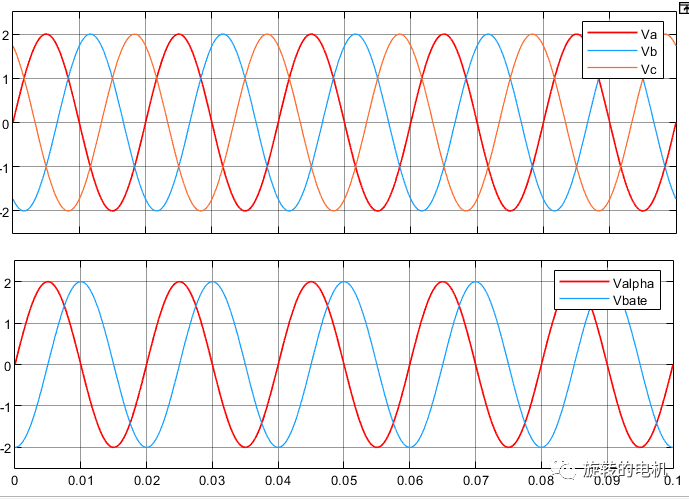
信號輸入:幅值為2,頻率為50Hz的三相正弦波信號
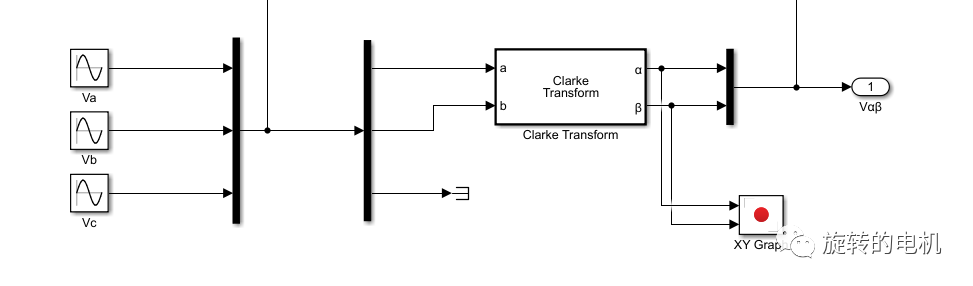
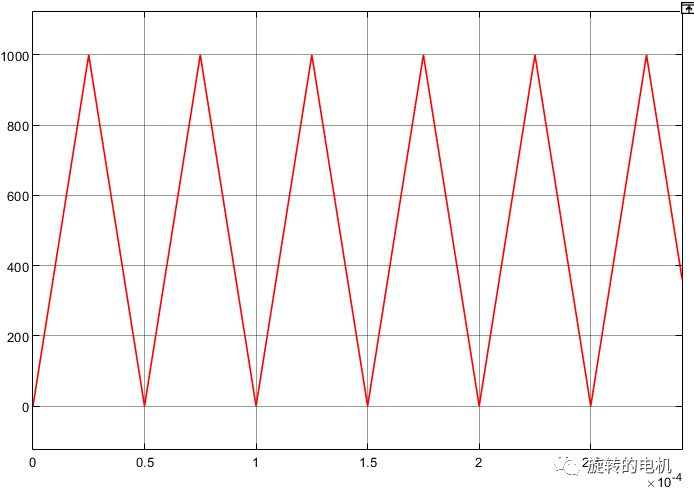
SVPWM算法實現:載波為20KHz的三角波,三相逆變電路的直流側電壓為24V
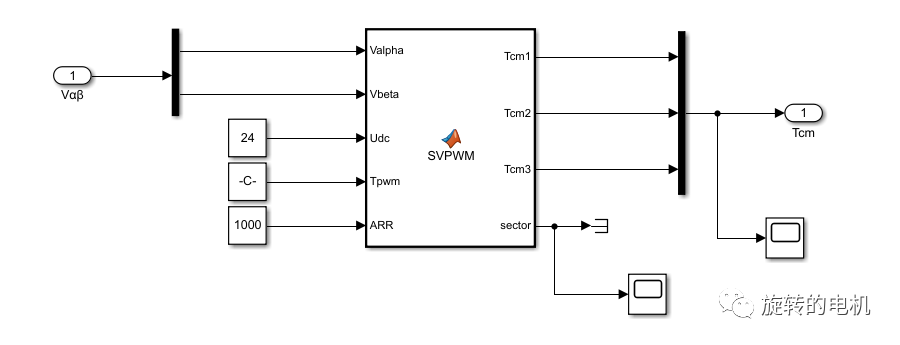
function [Tcm1,Tcm2,Tcm3,sector] = SVPWM(Valpha,Vbeta,Udc,Tpwm,ARR)
%輸出變量初始化
Tcm1 = 0;
Tcm2 = 0;
Tcm3 = 0;
sector = 0;
%扇區計算
%N與扇區對應的關系
% 3 1 5 4 6 2
% I II III IV V VI
Vref1 = Vbeta;
Vref2 = (sqrt(3)*Valpha-Vbeta)/2;
Vref3 = (-sqrt(3)*Valpha-Vbeta)/2;
if(Vref1>0)
sector = 1;
end
if(Vref2>0)
sector = sector+2;
end
if(Vref3>0)
sector = sector+4;
end
%扇區內合成矢量作用時間計算
X = sqrt(3)*Vbeta*Tpwm/Udc;
Y = Tpwm/Udc*(3/2*Valpha+sqrt(3)/2*Vbeta);
Z = Tpwm/Udc*(-3/2*Valpha+sqrt(3)/2*Vbeta);
switch(sector)
case 1
T1 = Z;T2 = Y;
case 2
T1 = Y;T2 = -X;
case 3
T1 = -Z;T2 = X;
case 4
T1 = -X;T2 = Z;
case 5
T1 = X;T2 = -Y;
otherwise
T1 = -Y;T2 = -Z;
end
%過調制處理
if(T1+T2>Tpwm)
T1 = Tpwm*T1/(T1+T2);
T2 = Tpwm*T2/(T1+T2);
else
T1 = T1;
T2 = T2;
end
%扇區內合成矢量切換點時間計算
%此處為7段式,兩個零矢量000 111 111插在中間,000均分插在兩端
ta = (Tpwm-(T1+T2))/4;
tb = ta+T1/2;
tc = tb+T2/2;
%輸出調制信號
switch(sector)
case 1
Tcm1 = tb;
Tcm2 = ta;
Tcm3 = tc;
case 2
Tcm1 = ta;
Tcm2 = tc;
Tcm3 = tb;
case 3
Tcm1 = ta;
Tcm2 = tb;
Tcm3 = tc;
case 4
Tcm1 = tc;
Tcm2 = tb;
Tcm3 = ta;
case 5
Tcm1 = tc;
Tcm2 = ta;
Tcm3 = tb;
case 6
Tcm1 = tb;
Tcm2 = tc;
Tcm3 = ta;
end
%調制信號處理,生成輸入到MCU中的調制信號
Tcm1 = 2*Tcm1/Tpwm;
Tcm2 = 2*Tcm2/Tpwm;
Tcm3 = 2*Tcm3/Tpwm;
Tcm1 = Tcm1*ARR;
Tcm2 = Tcm2*ARR;
Tcm3 = Tcm3*ARR;
end
PWM信號生成:載波為20KHz的三角波
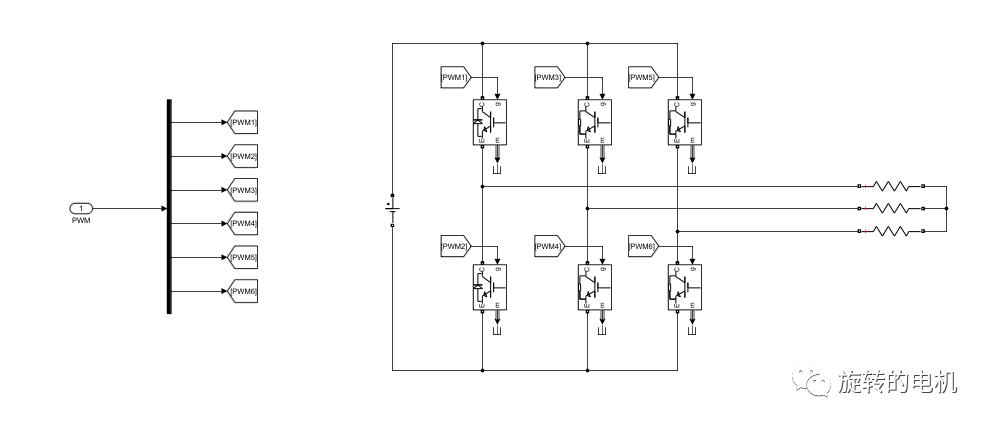
硬件電路:
8.2.仿真結果分析
電壓空間矢量的運動軌跡:
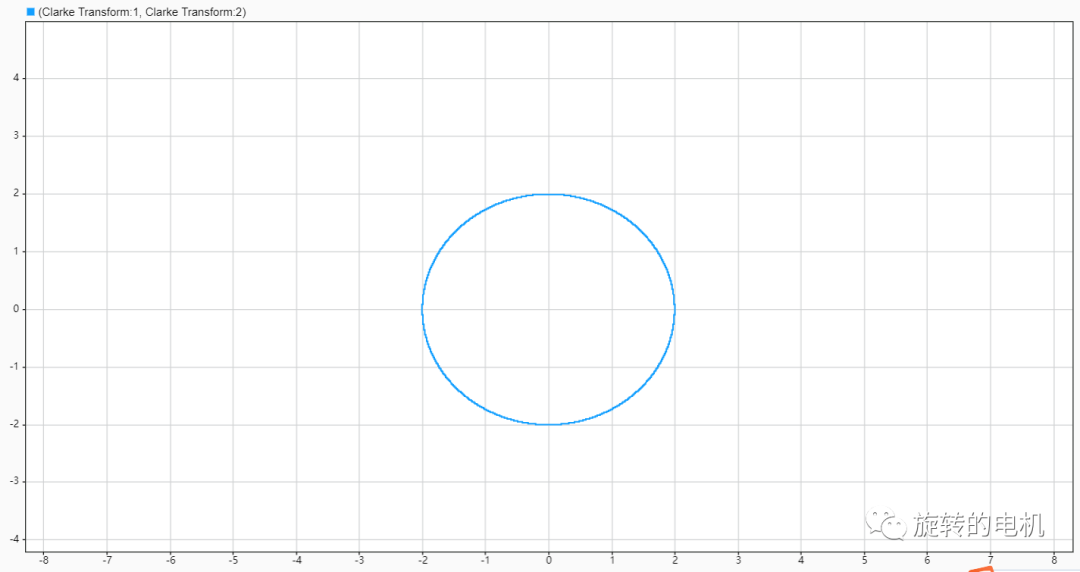
扇區判斷結果:
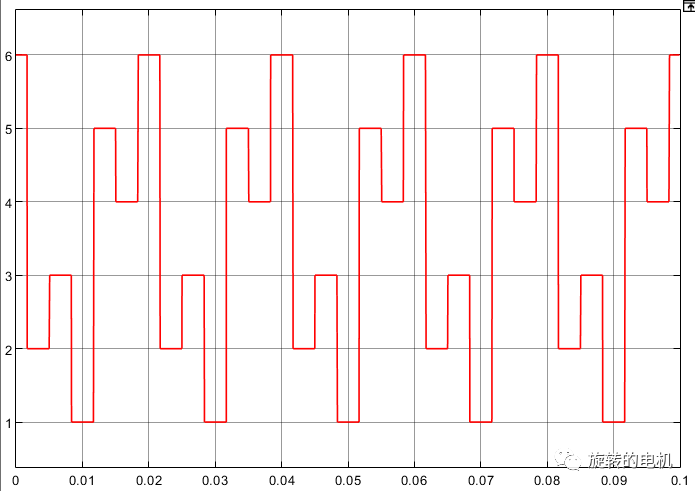
扇區內矢量切換點,即調制波波形:
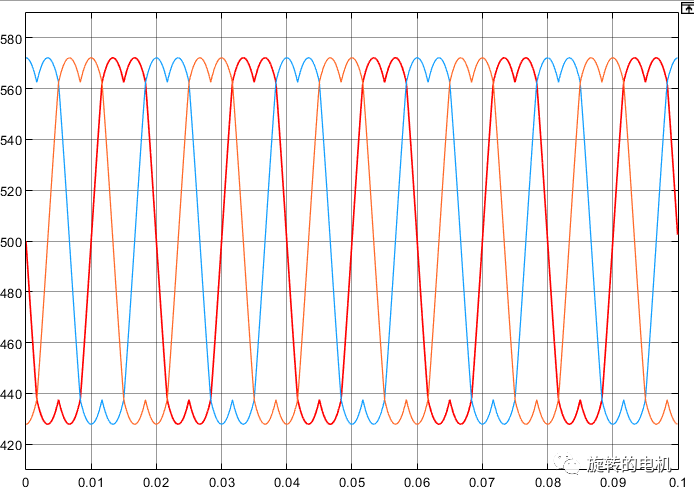
PWM信號:
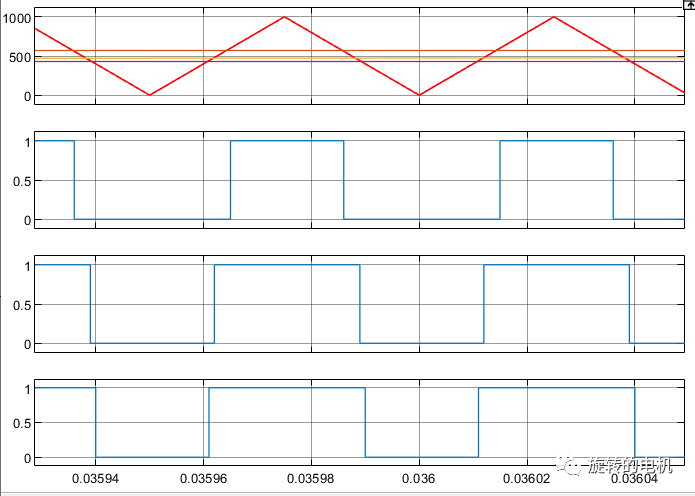
三相相電壓及濾波后的三相相電壓波形:生成的三相正弦電壓與期望的輸入電壓參數一致,幅值為2,頻率為50Hz。
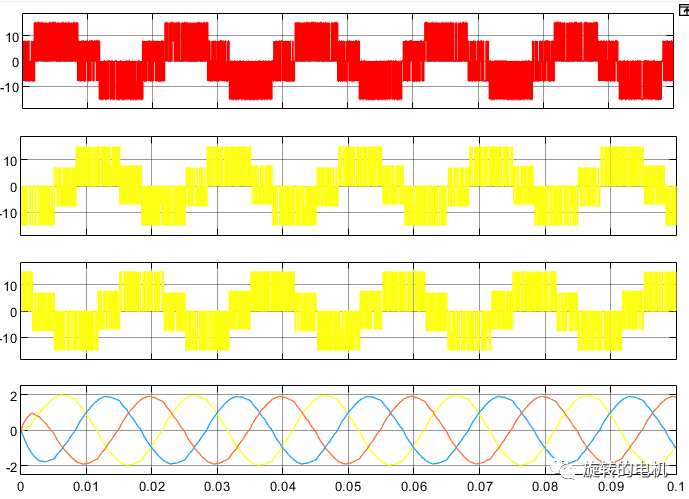
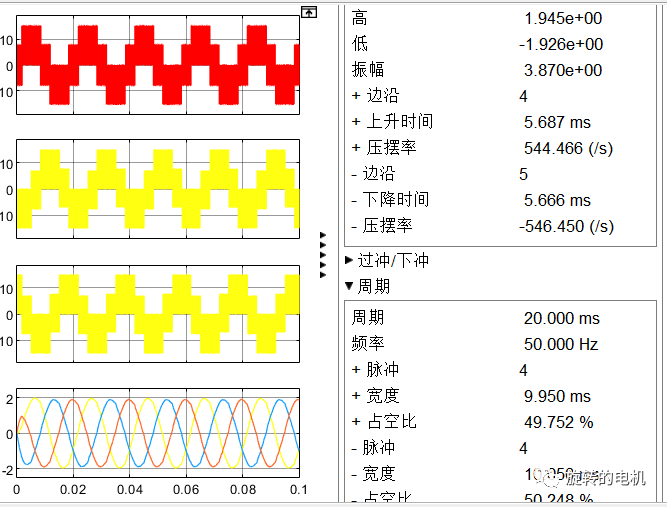
三相相電流及濾波后的三相相電流波形:
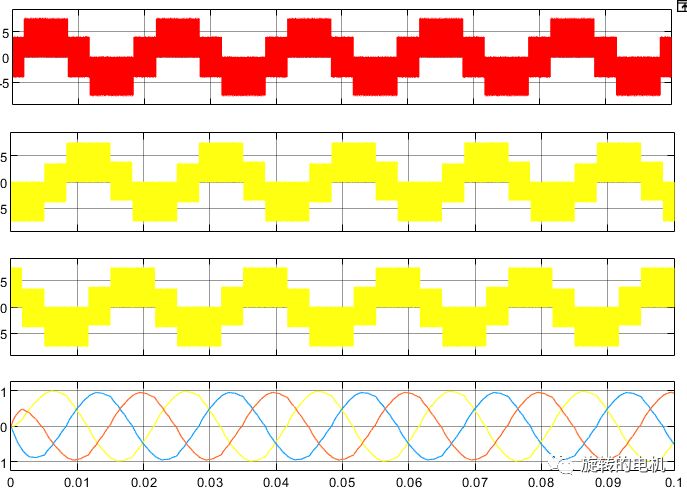
三相線電壓及濾波后的三相線電壓波形:
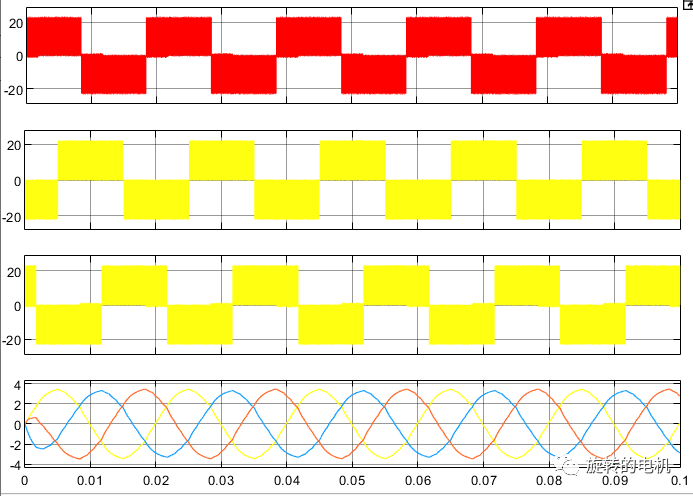
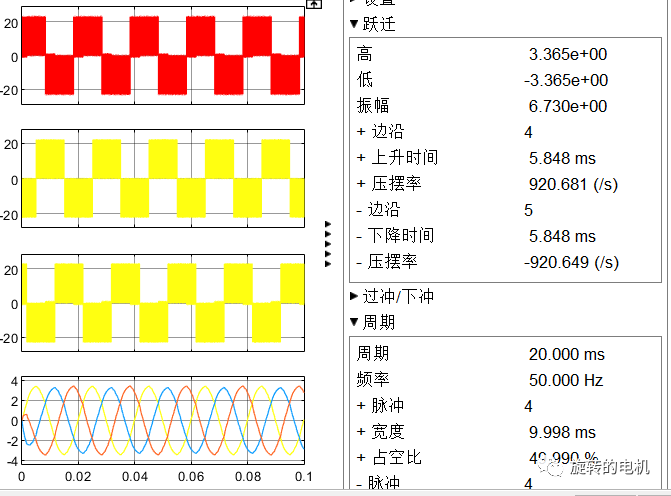
九、五段式SVPWM仿真分析
與上述7段式SVPWM算法的不同點就是,算法扇區切換點的時間不同,算法改動如下,其余部分同上述7段式SVPWM算法仿真。
function [Tcm1,Tcm2,Tcm3,sector] = SVPWM(Valpha,Vbeta,Udc,Tpwm,ARR)
%輸出變量初始化
Tcm1 = 0;
Tcm2 = 0;
Tcm3 = 0;
sector = 0;
%扇區計算
%N與扇區對應的關系
% 3 1 5 4 6 2
% I II III IV V VI
Vref1 = Vbeta;
Vref2 = (sqrt(3)*Valpha-Vbeta)/2;
Vref3 = (-sqrt(3)*Valpha-Vbeta)/2;
if(Vref1>0)
sector = 1;
end
if(Vref2>0)
sector = sector+2;
end
if(Vref3>0)
sector = sector+4;
end
%扇區內合成矢量作用時間計算
X = sqrt(3)*Vbeta*Tpwm/Udc;
Y = Tpwm/Udc*(3/2*Valpha+sqrt(3)/2*Vbeta);
Z = Tpwm/Udc*(-3/2*Valpha+sqrt(3)/2*Vbeta);
switch(sector)
case 1
T1 = Z;T2 = Y;
case 2
T1 = Y;T2 = -X;
case 3
T1 = -Z;T2 = X;
case 4
T1 = -X;T2 = Z;
case 5
T1 = X;T2 = -Y;
otherwise
T1 = -Y;T2 = -Z;
end
%過調制處理
if(T1+T2>Tpwm)
T1 = Tpwm*T1/(T1+T2);
T2 = Tpwm*T2/(T1+T2);
else
T1 = T1;
T2 = T2;
end
%扇區內合成矢量切換點時間計算
%此處為5段式,兩個零矢量000 111 111插在中間,000均分插在兩端
ta = 0;
tb = ta+T1/2;
tc = tb+T2/2;
%輸出調制信號
switch(sector)
case 1
Tcm1 = tb;
Tcm2 = ta;
Tcm3 = tc;
case 2
Tcm1 = ta;
Tcm2 = tc;
Tcm3 = tb;
case 3
Tcm1 = ta;
Tcm2 = tb;
Tcm3 = tc;
case 4
Tcm1 = tc;
Tcm2 = tb;
Tcm3 = ta;
case 5
Tcm1 = tc;
Tcm2 = ta;
Tcm3 = tb;
case 6
Tcm1 = tb;
Tcm2 = tc;
Tcm3 = ta;
end
%調制信號處理,生成輸入到MCU中的調制信號
Tcm1 = 2*Tcm1/Tpwm;
Tcm2 = 2*Tcm2/Tpwm;
Tcm3 = 2*Tcm3/Tpwm;
Tcm1 = Tcm1*ARR;
Tcm2 = Tcm2*ARR;
Tcm3 = Tcm3*ARR;
end
9.1.仿真結果分析
電壓空間矢量的運動軌跡:
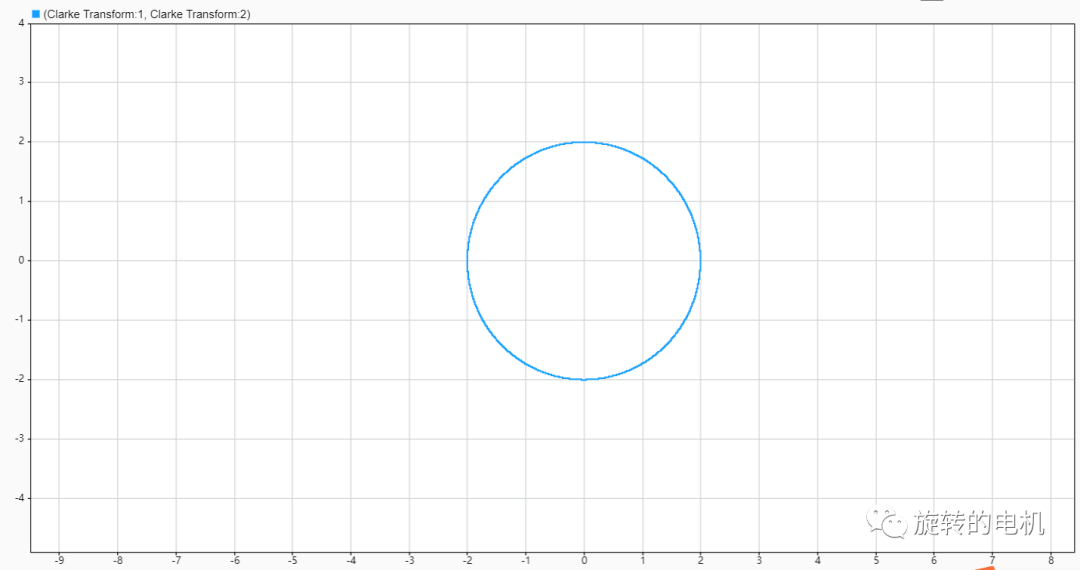
扇區判斷結果:
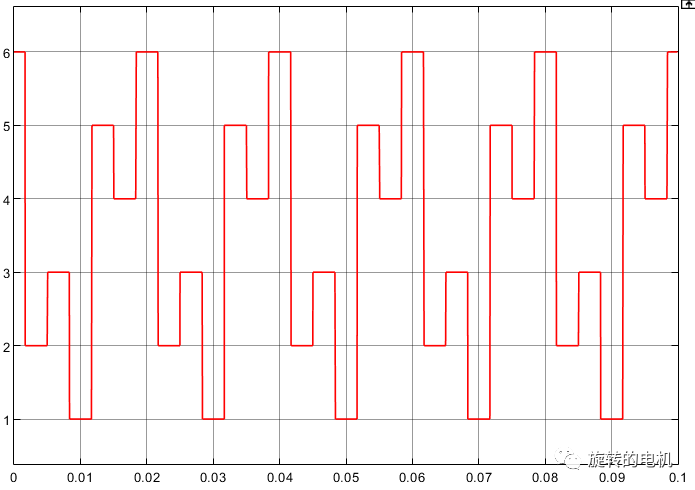
扇區內矢量切換點,即調制波波形:
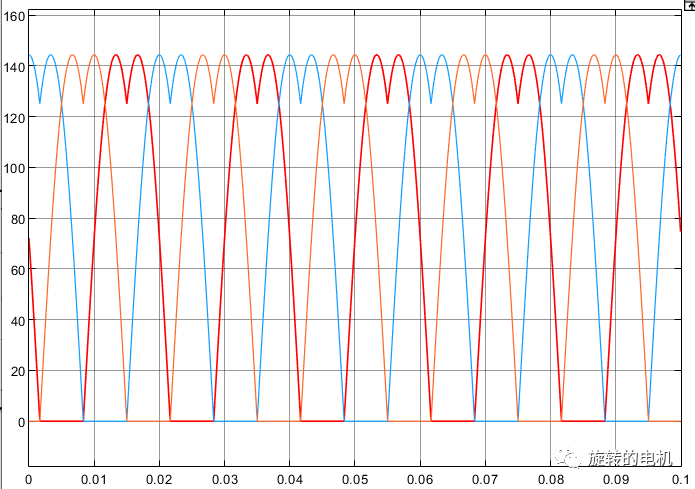
PWM信號:
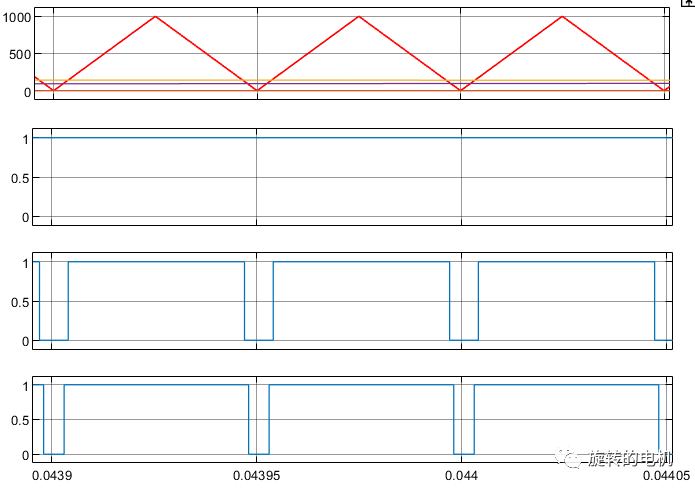
三相相電壓及濾波后的三相相電壓波形:生成的三相正弦電壓與期望的輸入電壓參數一致,幅值為2,頻率為50Hz。
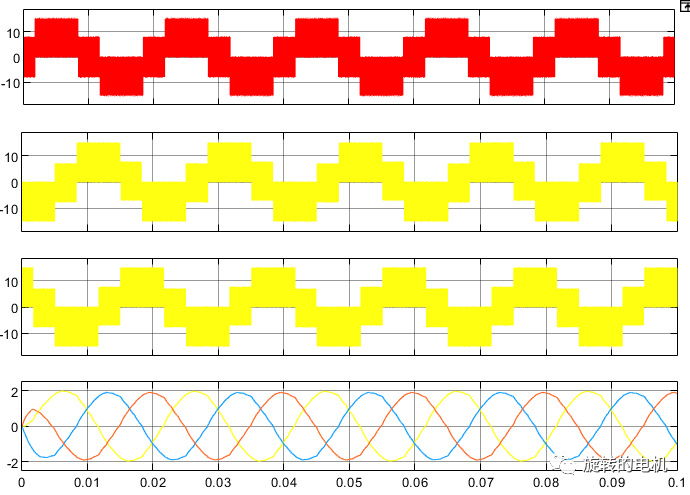
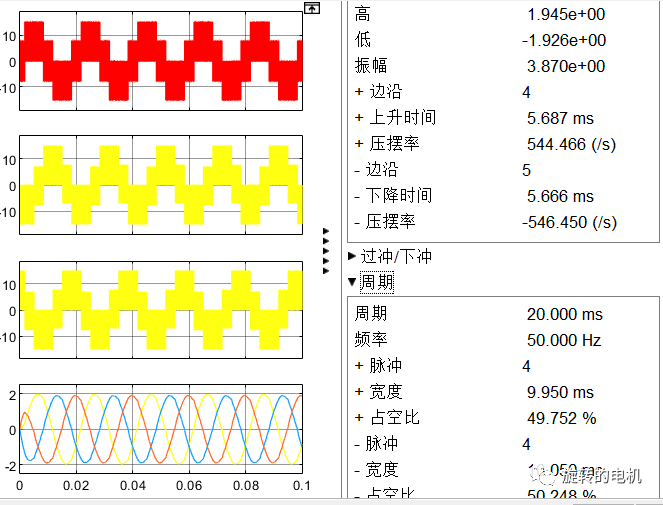
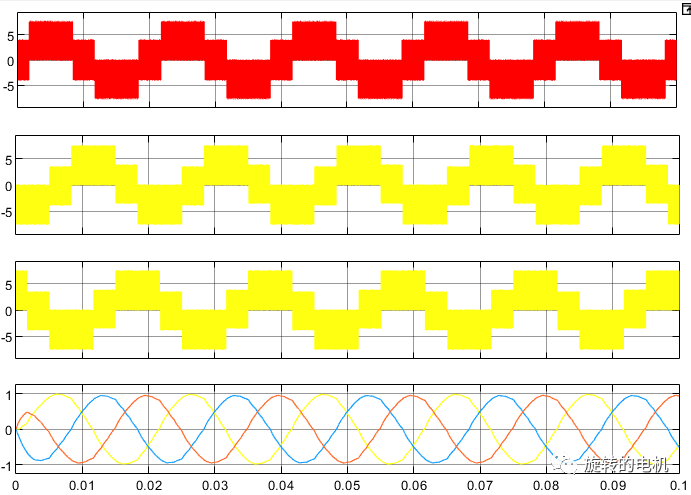
三相相電流及濾波后的三相相電流波形:
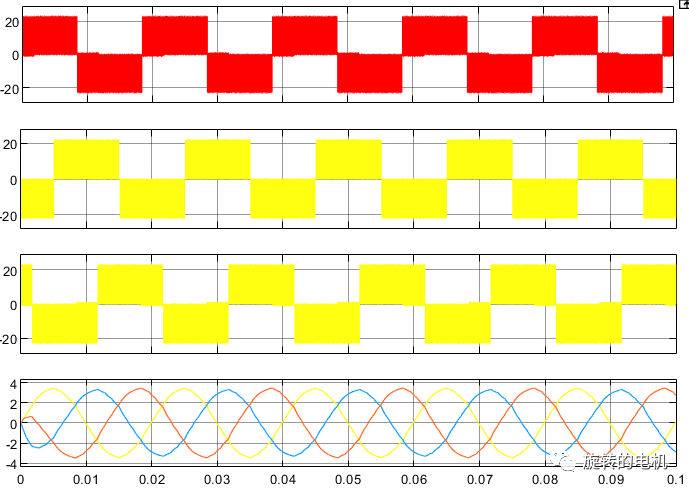
三相線電壓及濾波后的三相線電壓波形:
十、PMSM電壓開環控制Matlab/Simulink仿真分析
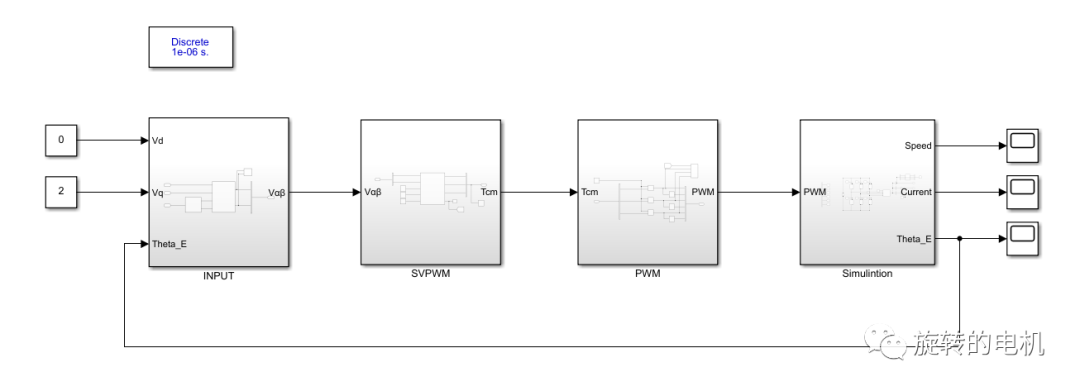
10.1.仿真電路分析
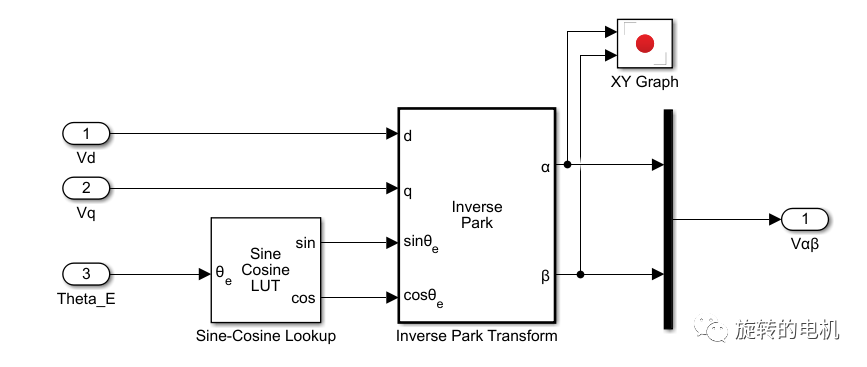
直接給定同步旋轉坐標系下Vd,Vq的電壓值實現永磁同步電機磁場定向的電壓開環控制
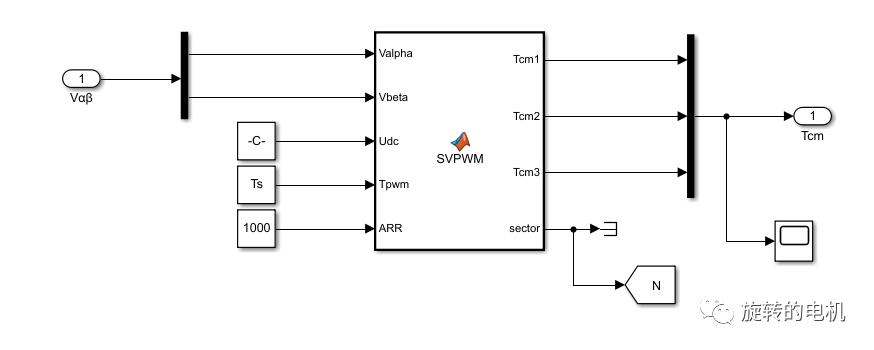
7段式SVPWM算法
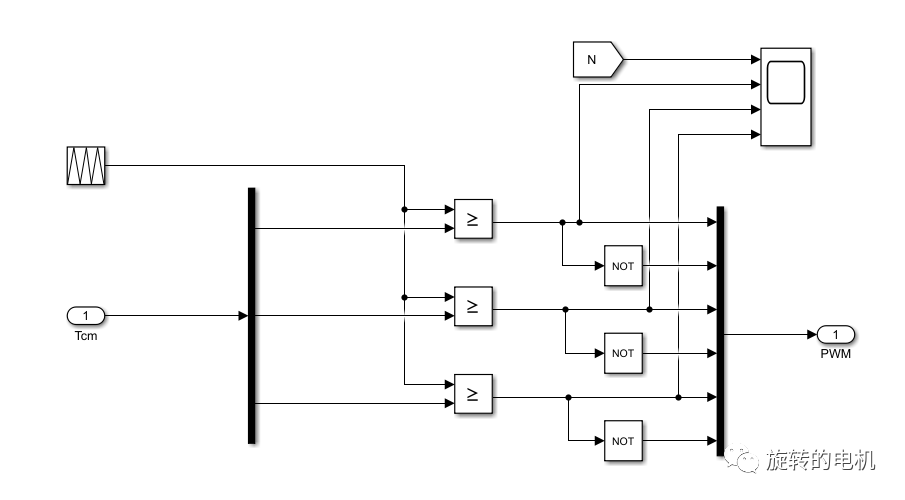
PWM控制信號生成
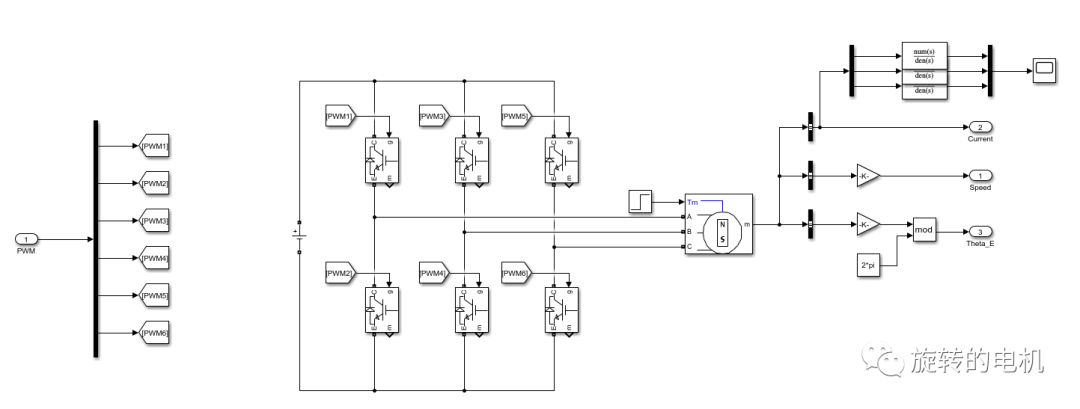
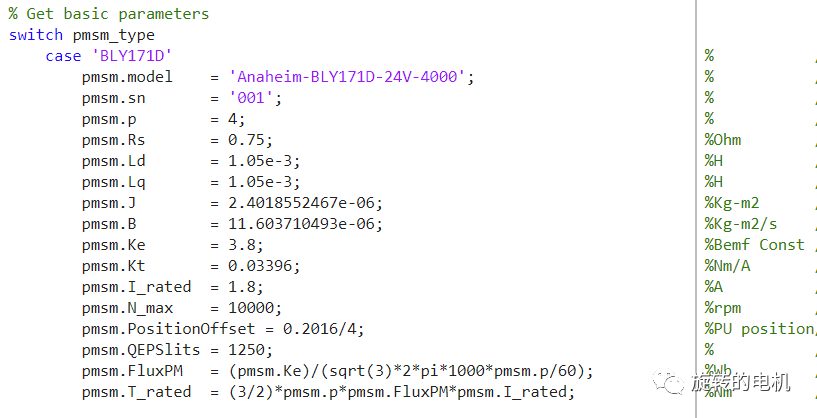
三相逆變電路及永磁同步電機,電機參數如下:
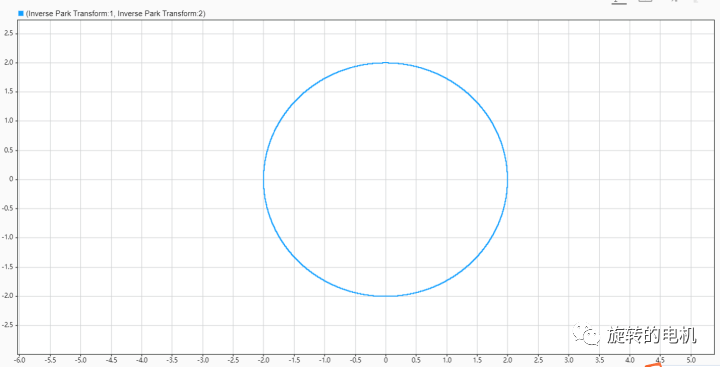
10.2.仿真結果分析
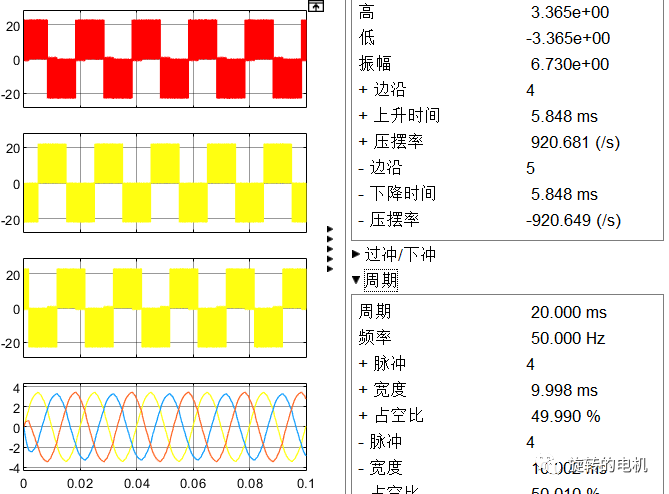
電壓空間矢量的運動軌跡:
扇區內矢量切換點,即調制波波形:
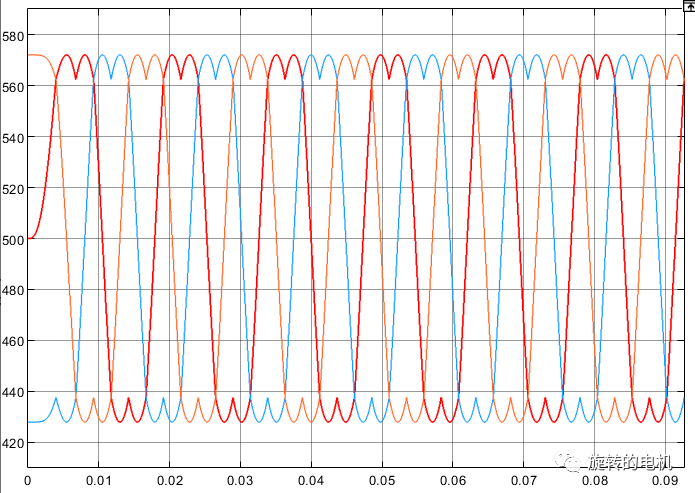
PWM信號:
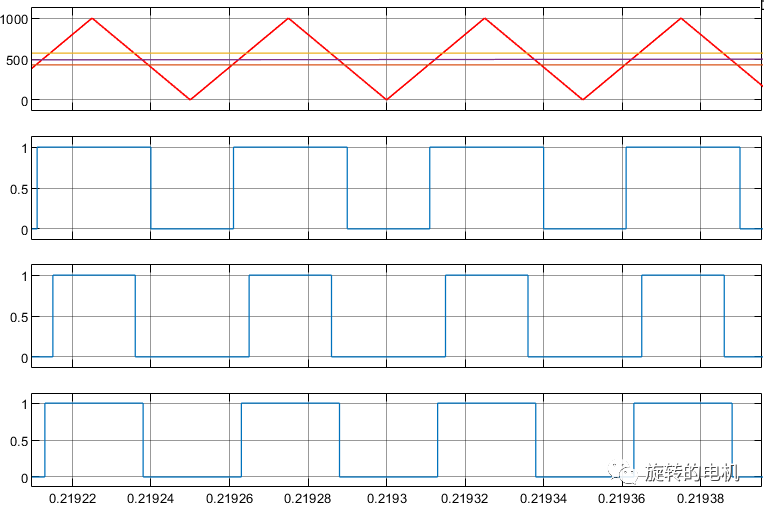
電機轉速:
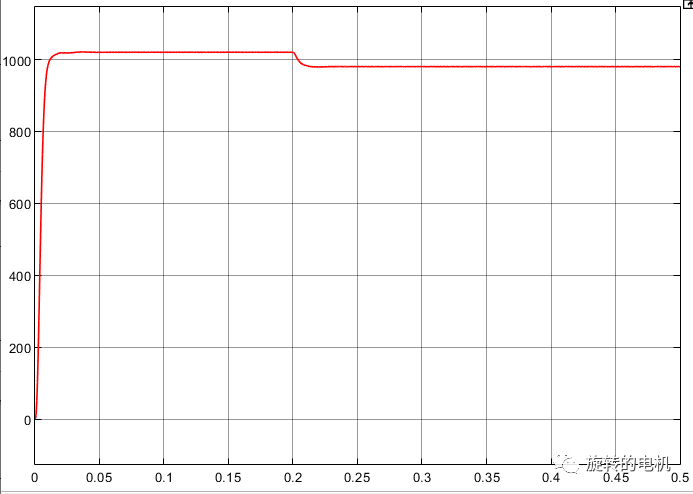
定子電流未濾波和濾波后的電流:
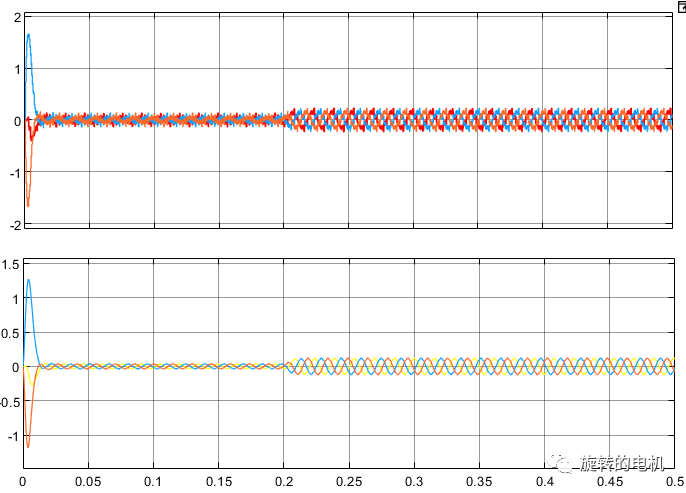
同步旋轉坐標系下的定子電流Id、Iq,未濾波和濾波后的電流:
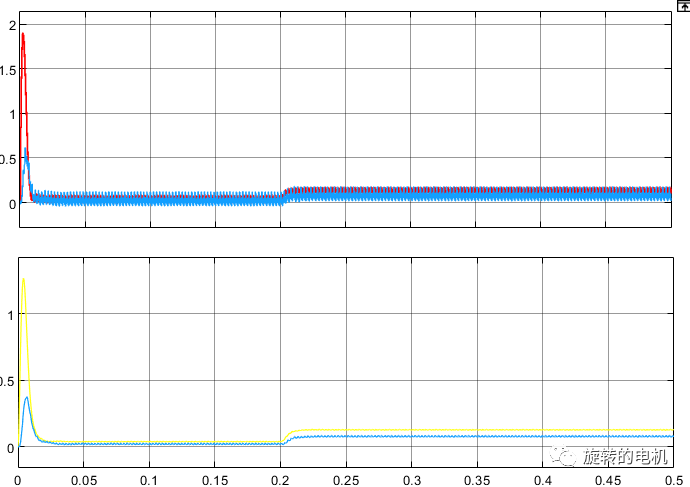
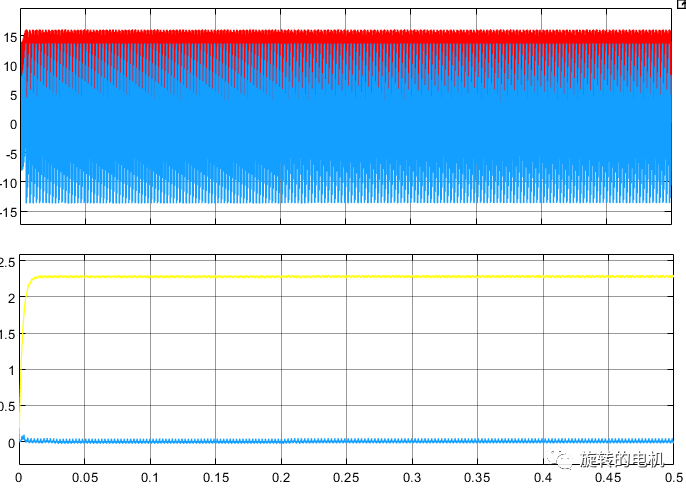
同步旋轉坐標系下的定子電壓Vd、Vq,未濾波和濾波后的電壓:
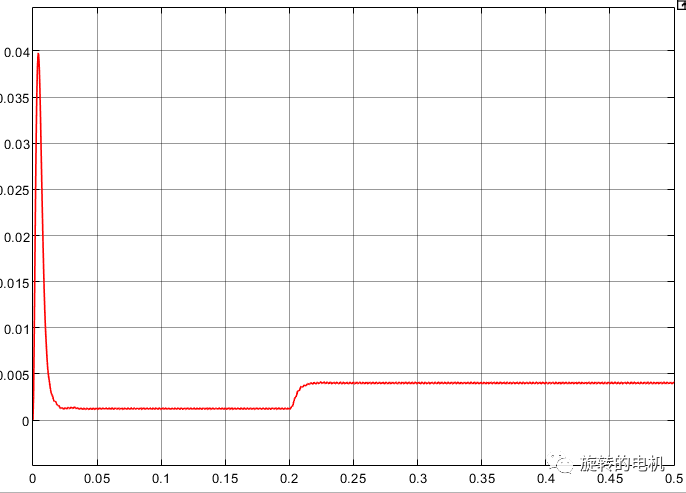
電磁轉矩:
總結
本章節首先介紹了SVPWM控制技術的原理,然后詳細分析了SVPWM控制算法的具體實現方式,并通過Matlab/Simulink對SVPWM控制算法進行了仿真分析,最后通過永磁同步電機矢量控制的實例進行了算法實現,為后續章節的分析奠定基礎。
-
matlab
+關注
關注
182文章
2963瀏覽量
230171 -
永磁同步電機
+關注
關注
28文章
868瀏覽量
49497 -
控制技術
+關注
關注
3文章
342瀏覽量
33145 -
Simulink
+關注
關注
22文章
522瀏覽量
62307 -
SVPWM
+關注
關注
14文章
614瀏覽量
90583
發布評論請先 登錄
相關推薦
基于MATLAB/Simulink的系統仿真技術與應用
【下載】《現代永磁同步電機控制原理及MATLAB仿真》——同步電機MATLAB仿真與技術分析
電路實驗與Matlab/Simulink仿真
SVPWM基本原理及數字實現
基于MATLAB/simulink的直接轉矩控制離散仿真系統的研究分析

Matlab與系統控制simulink仿真的PPT課件合集免費下載
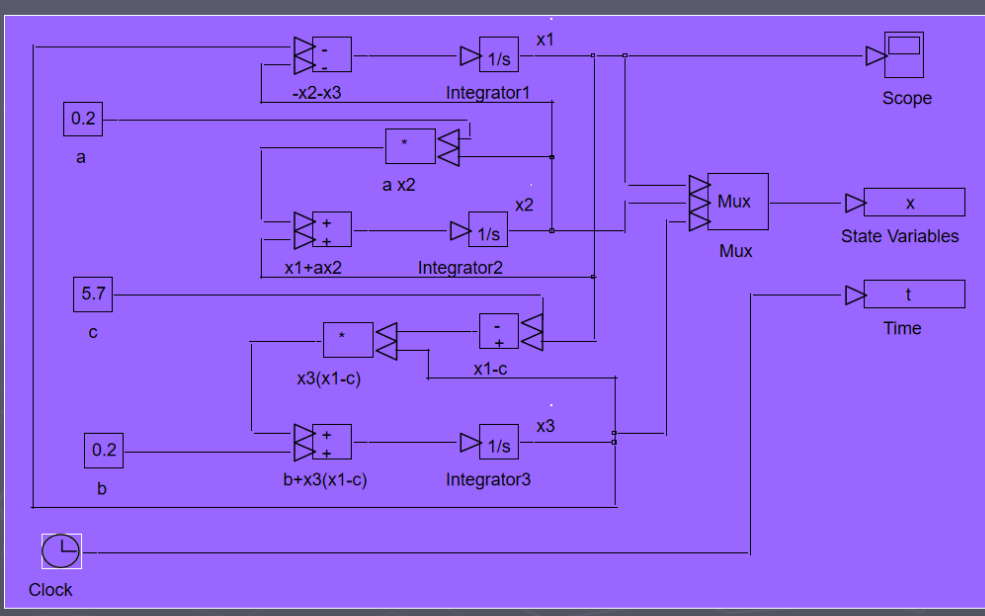
如何使用SIMULINK對SVPWM算法進行仿真
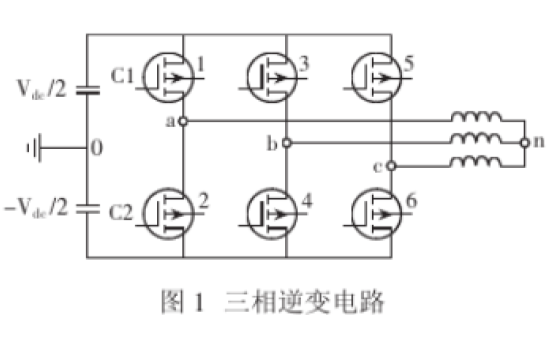
SVPWM逆變器Simulink仿真

永磁同步電機FOC控制的基本原理及Matlab/Simulink仿真分析
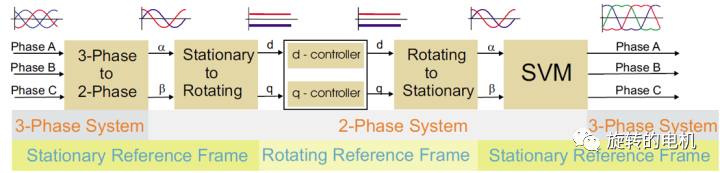




 SVPWM控制技術的基本原理及Matlab/Simulink仿真分析
SVPWM控制技術的基本原理及Matlab/Simulink仿真分析










評論