本文主要介紹原問題(PRIME PROBLEM)和對偶問題(DUAL PROBLEM),支持向量機優化問題可通過原問題向對偶問題的轉化求解。
一、原問題的定義
原問題的定義為:
最小化:f(ω);
限制條件:gi(ω)≤0,i=1~K;hi(ω)=0,i=1~M。
其中,ω為多維向量,限制條件中具有K個不等式(gi(ω)≤0),M個等式(hi(ω)=0)。
二、對偶問題的定義
首先定義函數:L(ω,α,β)=f(ω)+∑αigi(ω)+∑βihi(ω);
該函數向量形式的定義:L(ω,α,β)=f(ω)+αTg(ω)+βTh(ω);
該函數向量形式的定義中,α=[α1,α2,…,αK]T,β=[β1,β2,…,βM]T,g(ω)=[g1(ω),g2(ω),…,gK(ω)]T,h(ω)=[h1(ω),h2(ω),…,hM(ω)]T。
基于函數L(ω,α,β)的定義,原問題的對偶問題定義如下:
最大化:θ(α,β)=infL(ω,α,β);
限制條件:αi≥0,i=1~K。
其中,infL(ω,α,β)為遍歷所有ω后,取值最小的L(ω,α,β)。
三、定理一
根據以上定義,可得出定理一:
如果ω*是原問題的解,(α*,β*)是對偶問題的解,則有: f(ω*)≥θ(α*,β*)
該定理的證明如下: θ(α*,β*)=infL(ω,α*,β*)(將α*、β*代入對偶函數的定義)
≤L(ω*,α*,β*)(此步推導由于infL(ω,α*,β*)的取值最小)
=f(ω*)+α*Tg(ω*)+β*Th(ω*)(此步推導根據L(ω,α,β)的定義)
≤f(ω*)(此步推導由于原問題的限制條件gi(ω)≤0,hi(ω)=0,對偶問題的限制條件αi≥0)
四、強對偶定理
將f(ω*)-θ(α*,β*)定義為對偶差距(DUALITY GAP),根據上述定理,對偶差距是大于等于零的函數。
如果g(ω)=Aω+b,h(ω)=Cω+d,f(ω)為凸函數,則有f(ω*)=θ(α*,β*),此時對偶差距等于零。該定理為強對偶定理(STRONG DUALITY THEOREM)。
強對偶定理可更通俗地表述為:原問題的目標函數(f(ω))是凸函數,原問題的限制條件是線性函數,則原問題的解與對偶函數的解相等。
五、KKT條件
若f(ω*)=θ(α*,β*),則有: f(ω*)+α*Tg(ω*)+β*Th(ω*)=f(ω*); 即對于所有的i=1~K,要么αi=0,要么gi(ω*)=0(因為hi(ω)=0)。
該結論被稱為KKT條件,KKT分別代表先后獨立發現該結論的研究人員Karush、Kuhn、Tucker,該結論在Kuhn、Tucker發現后逐步被推廣。
審核編輯:劉清
-
向量機
+關注
關注
0文章
166瀏覽量
20798 -
機器學習
+關注
關注
66文章
8306瀏覽量
131834 -
GAP
+關注
關注
0文章
15瀏覽量
8281
原文標題:機器學習相關介紹(12)——支持向量機(原問題和對偶問題)
文章出處:【微信號:行業學習與研究,微信公眾號:行業學習與研究】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦


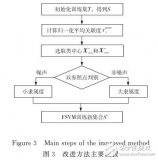
基于改進支持向量機的貨幣識別研究
基于支持向量機(SVM)的工業過程辨識
基于向量機隨機投影特征降維分類下降解決方案
多分類孿生支持向量機研究進展
支持向量機的故障預測模型
什么是支持向量機 什么是支持向量




 支持向量機(原問題和對偶問題)
支持向量機(原問題和對偶問題)
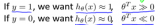
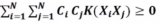










評論