點擊上方藍字關注我們
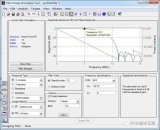
本文將回顧對稱 FIR濾波器的高效 FPGA 實現的注意事項。
本文將推導對稱 FIR 濾波器的模塊化流水線結構。我們將看到派生結構可以使用XilinxFPGA 的 DSP 片有效地實現。
對稱 FIR 濾波器
讓我們考慮一個八階 FIR 濾波器。該濾波器的傳遞函數為
$$Y(z)= sum_{k=0}^{7} z^{-k} h_k X(z)$$
假設濾波器是對稱的,并且我們有 $$h_k = h_{7-k}$$ 對于 $$k=0, 1, dots ,7$$。因此,傳遞函數可以改寫為
$$Y(z)= (1+z^{-7})h_0X(z)+(z^{-1}+z^{-6})h_1X(z)+(z^{-2}+ z^{-5})h_2X(z)+ (z^{-3}+z^{-4})h_3X(z)$$
公式 1
我們可以將公式 1 實現為具有四級流水線的系統,如圖 1 所示。此框圖的每個階段對應于公式 1 的四項之一。

圖 1. 點擊放大。
由于我們插入了三個寄存器組來執行流水線操作,因此我們預計會有三個時鐘周期的延遲。就 z 變換而言,圖 1 的輸出將是 $$z^{-3}$$ 乘以 $$Y(z)$$(如公式 1 所示)。換句話說,我們有 $$sig7=z^{-3}Y(z)$$。因此,我們有
$$egin{align}
sig7 &= z^{-3}(1+z^{-7})h_0X(z)
+z^{-3}(z^{-1}+z^{-6 })h_1X(z)
&+z^{-3}(z^{-2}+z^{-5})h_2X(z) + z^{-3}(z^{-3}+ z^{-4})h_3X(z)
end{對齊}$$
公式 2
現在,我們應該將這四項中的每一項分配到圖 1 中的適當階段。我們有輸出 sig7 的方程式,因此首先設計系統的階段會更容易。如果我們將術語 $$z^{-3}(1+z^{-7})h_0X(z)$$ 實現為階段 4,我們將必須級聯十個延遲元件來實現 $$z^{- 10}$$。但是,如果我們將 $$z^{-3}(z^{-3}+z^{-4})h_3X(z)$$ 實現為階段 4,我們將只需要七個延遲元件的級聯。因此,我們將方程式 2 的一項實現為圖 1 的階段 4。這給出了圖 2 中所示的電路。
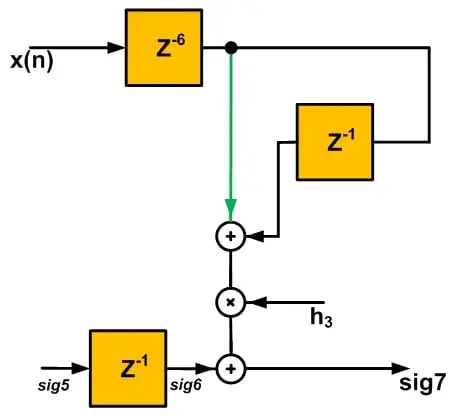
圖 2
因此,我們得到
$$sig6 = z^{-3}(1+z^{-7})h_0X(z)
+z^{-3}(z^{-1}+z^{-6})h_1X(z) +z^{-3}(z^{-2}+z^{-5})h_2X(z)$$
這使
$$sig5 = z^{-2}(1+z^{-7})h_0X(z)
+z^{-2}(z^{-1}+z^{-6})h_1X(z) +z^{-2}(z^{-2}+z^{-5})h_2X(z)$$
現在,就像第 4 階段一樣,我們可以推導出圖 1 的第 3 階段并獲得圖 3 中的電路。
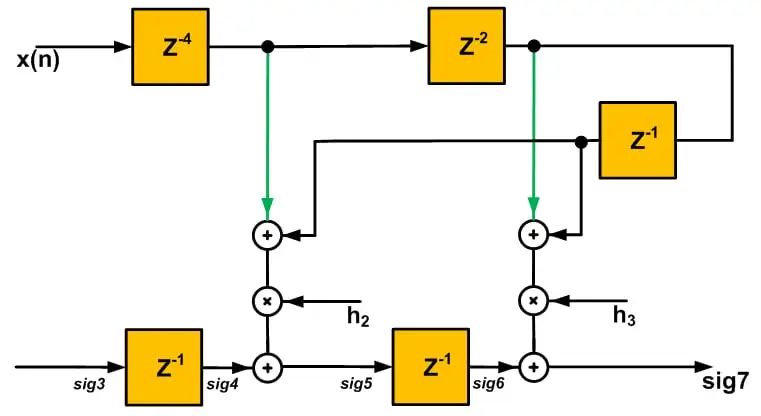
圖 3
現在,我們有
$$sig3 = z^{-1}(1+z^{-7})h_0X(z)
+z^{-1}(z^{-1}+z^{-6})h_1X(z) $$
可以改寫為
$$sig3 = z^{-1}sig1
+z^{-1}(z^{-1}+z^{-6})h_1X(z)$$
在哪里
$$sig1 = (1+z^{-7})h_0X(z)$$
使用這兩個方程,我們可以找到圖 4 所示的終結構。
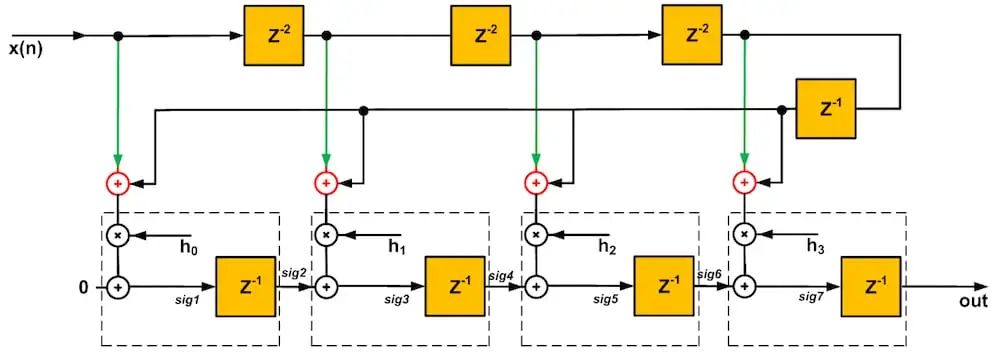
圖 4.點擊放大。
請注意,對于級,包含一個零輸入的加法器,以強調原理圖的模塊化和規則結構。此外,在 sig7 之后放置了一個額外的延遲元件。如您所見,虛線框內的電路在結構的每個階段都重復出現。這種模塊化結構是理想的,因為它便于擴展結構以用于任意數量的抽頭。
Xilinx 在其高性能 FPGA 中將虛線框內的電路實現為 DSP slice。這些DSP Slice可以高效級聯;這就是為什么可以使用多個切片來實現給定的 FIR 濾波器的原因。在下一節中,我們將回顧 DSP48 Slice 的結構。
賽靈思 DSP Slice
DSP Slice 是多種元素,實現圖 4 的 FIR 濾波器只是眾多可能應用中的一種。圖 5 顯示了 Virtex-4 器件中 DSP48 片的框圖。
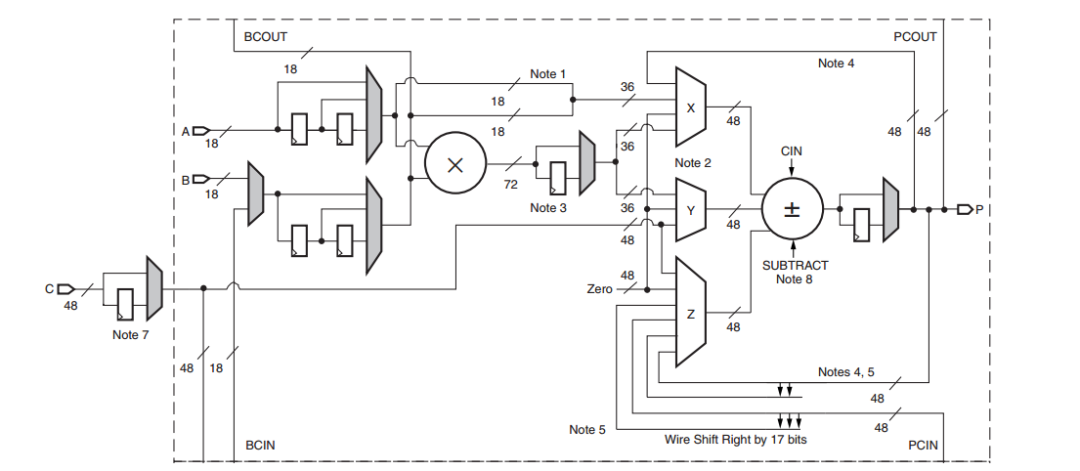
圖 5. Virtex-4 器件中 DSP48 片的框圖。圖片由賽靈思提供。點擊放大。
加法器/減法器的輸出方程為
$$Adder Out= Big ( Z pm (X+Y+C_{in}) Big )$$
其中 X、Y 和 Z 表示相應多路復用器的輸出值。多路復用器允許我們為加法器/減法器選擇不同的輸入。乘法是 DSP Slice 的典型應用。例如,我們可以配置 DSP48 slice 來實現以下等式:
$$Adder Out = C pm (A imes B + C_{in})$$
當使用乘法器功能時,X 和 Y 多路復用器的輸出必須饋送到加法器,因為方框圖中所示的乘法器生成兩個部分結果,這些結果由加法器/減法器組合以產生終的乘法結果。有關詳細信息,請參閱 Xilinx 的書 DSP:設計以獲得結果的第 21 頁。
slice 不同輸入路徑中的寄存器允許我們進行流水線設計。例如,我們可以直接將輸入 A 應用于 slice 的數學部分,其路徑中沒有寄存器,或者我們可以在其路徑中放置一個或兩個寄存器。這是通過可以從寄存器之前或之后選擇輸入的多路復用器(參見圖 5)實現的。
DSP 切片(圖 5 中標記為“P”)的輸出可以應用于同一切片的加法器/減法器以實現累加器。
如圖 5 所示,DSP Slice 支持多種功能,包括乘法、乘法后累加、全流水線乘法和循環桶式移位。DSP48 Slice 的更版本包含一些修改,例如包括預加器塊,這使得 Slice 更加通用。例如,預加器可用于實現對稱 FIR 濾波器(如上所述)。請注意,DSP slice 旨在有效地實現上述功能。這就是為什么與使用 FPGA 通用結構的設計相比,基于 DSP 片的設計可以實現更低的功耗、更高的性能和更高效的硅片利用率。有關 Xilinx DSP slice 的更多詳細信息,請參閱上述書籍。
使用 DSP Slice 實現對稱 FIR 濾波器
下面的圖 6 顯示了圖 5 的 DSP slice 的簡化框圖。
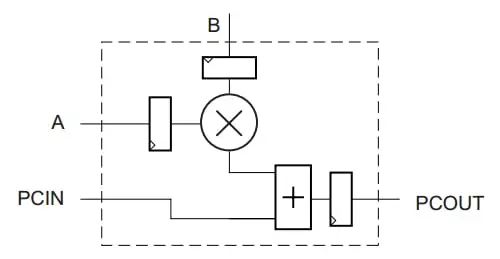
圖 6
這個簡化的框圖強調了一個 slice 的輸出可以作為輸入路由到下一個 slice 的加法器/減法器。如果我們忽略圖 6 中所示的輸入寄存器,則圖 6 的原理圖與圖 4 的虛線框內的電路相同。因此,通過級聯這些 DSP slice,我們可以有效地實現圖 4 的 FIR 濾波器。在這個在這種情況下,我們可以使用 FPGA 的通用結構切片來實現紅色加法器(參見圖 4)。
圖 7 顯示了使用 7 系列 DSP48 片的圖 4 的實現。
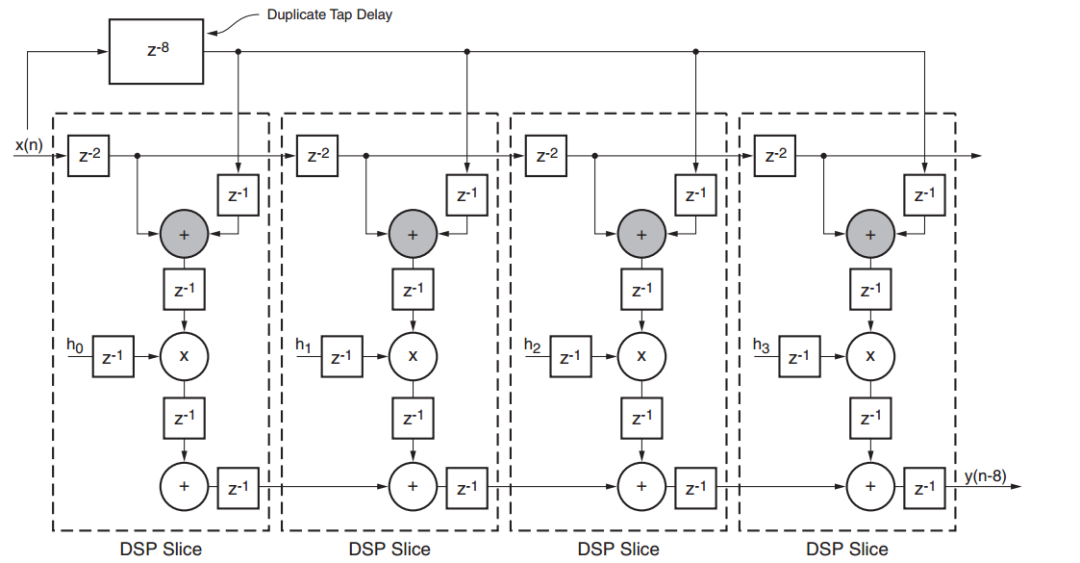
圖 7. 八抽頭對稱 FIR 濾波器的基于 DSP48 的實現。圖片由賽靈思提供。點擊放大。
此處,帶陰影的加法器實現了圖 4 中的紅色加法器,延遲線可以使用片內的寄存器實現。您可以在此處圖 7 電路的 Xilinx VHDL 代碼(如果單擊此鏈接,將立即開始)。
結論
我們推導出用于對稱 FIR 濾波器的模塊化流水線結構。我們還研究了 Xilinx DSP slice 的結構,它可用于實現多種功能,包括乘法、乘法后累加、全流水線乘法和循環桶式移位。7 系列 DSP48 Slice 更加通用,可以更高效地實施對稱 FIR 濾波器。



掃取二維碼獲取
更多精彩
FPGA設計論壇
往期推薦
歡迎關注至芯科技
至芯官網:www.zxopen.com
至芯科技技術論壇:www.fpgaw.com
至芯科技淘寶網址:
https://zxopen.taobao.com
至芯科技FPGA初級課程(B站):
https://space.bilibili.com/521850676
至芯科技FPGA在線課程(騰訊課堂):
https://zxopenbj.ke.qq.com/
至芯科技-FPGA 交流群(QQ):282124839
掃碼加微信邀請您加入FPGA學習交流群


歡迎加入至芯科技FPGA微信學習交流群,這里有一群優秀的FPGA工程師、學生、老師、這里FPGA技術交流學習氛圍濃厚、相互分享、相互幫助、叫上小伙伴一起加入吧!

點個

在看
你最好看
原文標題:FPGA 實現線性相位 FIR 濾波器的注意事項
文章出處:【微信公眾號:FPGA設計論壇】歡迎添加關注!文章轉載請注明出處。
-
FPGA
+關注
關注
1626文章
21666瀏覽量
601830
原文標題:FPGA 實現線性相位 FIR 濾波器的注意事項
文章出處:【微信號:gh_9d70b445f494,微信公眾號:FPGA設計論壇】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
請問OPA211用在VCO環路濾波器上有哪些注意事項?
FIR濾波器的工作原理和特點
如何區分IIR濾波器和FIR濾波器
iir濾波器和fir濾波器的優勢和特點
基于matlab FPGA verilog的FIR濾波器設計
matlab與FPGA數字信號處理系列 Verilog 實現并行 FIR 濾波器
Vivado 使用Simulink設計FIR濾波器
Vivado經典案例:使用Simulink設計FIR濾波器
電源濾波器接線的注意事項
濾波器的主要功能和使用注意事項:展示其的重要性

電源濾波器的選購、安裝和使用注意事項有哪些?





 FPGA 實現線性相位 FIR 濾波器的注意事項
FPGA 實現線性相位 FIR 濾波器的注意事項
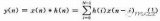











評論