在RC電路中,在特定配置中使用組合或R(電阻)和C(電容器),以調節電流,以實現所需的條件。
電容器的主要用途之一是耦合單元的形式,它允許交流通過但阻止直流電。在幾乎任何實際電路中,您都會看到一些電阻與電容器串聯。
電阻限制了電流的流動,并通過使電容器中電荷與饋電電壓成比例,在饋入電容器的電源電壓上造成一些延遲。
RC 時間常數
確定RC時間(T)的公式非常簡單:
T = RC,其中 T = 以秒為單位的時間常數 R = 電阻,單位為兆歐 C = 電容(以微法拉為單位)。
(可以觀察到,如果R以歐姆為單位,C以法拉為單位,則T的數值完全相同,但在實踐中,兆歐和微法拉通常是更容易的單位。
在RC電路中,RC時間常數可以定義為電容器兩端施加的電壓達到施加電壓的63%所花費的時間。
(這個63%的星等實際上是為了便于計算而首選的)。在現實生活中,電容器兩端的電壓可能會繼續累積到實際上(但永遠不會完全)施加電壓的100%,如下圖所示。

時間常數元素以時間因子的形式表示時間長度,例如在RC網絡的1個時間因子處,累積63%的總電壓,在2X時間常數之后的時間段內,電容器內部建立80%的總電壓;等等。
在時間常數為5之后,幾乎(但不完全)100%的電壓可能會在電容器上建立。電容器的放電因數以相同的基本方式出現,但順序相反。
這意味著,在等于時間常數5的時間間隔后,施加到電容器上的電壓將達到全電壓的100 - 63 = 37%的下降,依此類推。
電容器永遠不會充滿電或放電
從理論上講,至少電容器絕不能充電到完全施加的電壓水平;它也不能完全排出。
實際上,完全充電或完全放電可以被視為在對應于 5 個時間常數的時間段內完成。
因此,在如下圖所示的電路中,為開關1供電將在5倍時間常數秒內對電容器進行“完全”充電。

接下來,當開關1打開時,電容器可能處于存儲等于實際施加電壓的電壓的情況。如果電容器的內部漏電流為零,它將無限期地保持這種電荷。
這種失去電荷的過程實際上非常緩慢,因為在現實世界中沒有電容器是完美的,但是在某些相當長的時間段內,這種存儲的電荷可能會繼續成為原始“完全充電”電壓的有效來源。
當電容器施加高電壓時,即使在電路斷電后,它也可以迅速處于觸碰到電擊的位置。
為了執行上圖第二張圖形所示的充電/放電周期,當開關2閉合時,電容器通過連接的電阻開始放電,并且需要一段時間才能完成其放電過程。
松弛振蕩器中的RC組合

上圖是一個非常基本的松弛振蕩器電路,使用電容器的基本電荷放電理論工作。
它包括一個串聯到直流電壓源的電阻器 (R) 和電容器 (C)。為了能夠從物理上看到電路的工作情況,霓虹燈與電容器并聯使用。
燈的行為幾乎像開路一樣,直到電壓達到其閾值電壓限制,這時它立即打開并像導體一樣傳導電流并開始發光。因此,該電流的電源電壓源必須高于氖觸發電壓的電源電壓源。
當電路上電時,電容器根據RC時間常數緩慢開始充電。燈開始接收在電容器兩端產生的上升電壓。
當電容器上的電荷達到可能等于氖燈的點火電壓的值時,霓虹燈就會傳導并開始點亮。
發生這種情況時,氖燈為電容器創建放電路徑,現在電容器開始放電。這反過來又會導致霓虹燈兩端的電壓下降,當該電平低于霓虹燈的點火電壓時,燈會關閉并關閉。
該過程現在繼續導致霓虹燈閃爍 ON OFF。閃爍速率或頻率取決于RC時間常數值,可以對其進行調整以啟用慢速閃爍或快速閃爍速率。
如果我們考慮如圖所示的元件值,電路的時間常數 T = 5(兆歐)x 0.1(微法拉)= 0.5 秒。
這意味著通過更改RC值,可以根據個人喜好相應地更改霓虹燈的閃爍率。
交流電路中的 RC 配置
當交流電用于RC配置時,由于電流的交流性質,交流電的一個半周期有效地為電容器充電,同樣,它與下一個負半周期放電。這導致電容器根據交流周期波形的不同極替充電和放電。
因此,實際上,交流電壓不會存儲在電容器中,而是允許通過電容器。然而,這種電流的通過受到電路路徑中現有RC時間常數的限制。
RC元件決定電容器充電和放電的施加電壓的百分比。同時,電容器還可以通過電抗的方式為交流電的通過提供輕微的電阻,即使這種電抗基本上不消耗任何功率。它的主要影響是RC電路中涉及的頻率響應。
交流電路中的RC耦合
通過電容器將音頻電路的特定級耦合到另一級是一種常見且廣泛的實現方式。雖然電容似乎是獨立使用的,但實際上它可能涉及由術語“負載”表示的積分串聯電阻,如下所示。

該電阻在電容器的幫助下,產生了RC組合,該組合可能負責產生一定的時間常數。
至關重要的是,該時間常數補充了從一個級傳輸到另一級的輸入交流信號頻率的規格。
如果我們假設以音頻放大器電路為例,輸入頻率的最高范圍可能約為10 kHz。這種頻率的時間段周期將為 1/10,000 = 0.1 毫秒。
也就是說,為了允許該頻率,每個周期在耦合電容功能方面實現兩個充電/放電特性,一個是正極,一個是負極。
因此,單獨充電/放電功能的時間段將為 0.05 毫秒。
啟用此功能所需的RC時間常數必須滿足0.05毫秒值才能達到饋電交流電壓電平的63%,并且基本上略低于允許高于63%的施加電壓的通過。
優化 RC 時間常數
上述統計數據為我們提供了有關要使用的耦合電容器的最佳可能值的想法。
為了說明這一點,假設低功耗晶體管的正常輸入電阻約為1 k。最有效的RC耦合的時間常數可能是0.05毫秒(見上文),這可以通過以下計算來實現:
0.05 x 10 = 1,000 x C 或 C = 0.05 x 10-9法拉 = 0.50 pF(或可能略低,因為這將允許高于 63%
的電壓通過電容器)。
實際上,通常可以實現更大的電容值;可以大到1μF甚至更多。這通常可以提供改進的結果,但相反,可能導致交流耦合傳導效率降低。
此外,計算表明,當在耦合電路中實現實際電容器時,隨著交流頻率的增加,容性耦合的效率越來越低。
在濾波電路中使用RC網絡
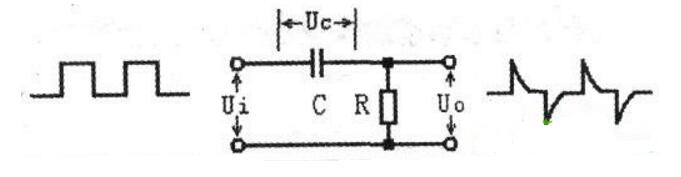
下圖演示了作為濾波器電路實現的標準RC布置。

如果我們看一下輸入側,我們會發現一個電阻與容抗串聯,導致兩個元件上產生壓降。
如果電容器電抗(Xc)恰好高于R,則幾乎所有的輸入電壓都會在電容器上積聚,因此輸出電壓達到等于輸入電壓的水平。
我們知道電容電抗與頻率成反比,這意味著,如果交流頻率增加會導致電抗降低,導致輸出電壓的比例性增加(但輸入電壓的很大一部分會被電阻降低)。
什么是臨界頻率
為了確保交流信號的有效耦合,我們必須考慮稱為臨界頻率的因素。
在此頻率下,電抗值元件往往會受到嚴重影響,以至于在這種情況下,耦合電容開始阻塞信號,而不是有效導通。
在這種情況下,伏特(輸出)/伏特(輸入)的比率開始迅速下降。下面以基本的圖表形式演示了這一點。

臨界點,稱為滾降點或截止頻率(f),評估如下:
fc = 1 / 2πRC
其中 R 以歐姆為單位,C 以法拉為單位,π = 3.1416
但是從前面的討論中我們知道RC = 時間常數T,因此方程變為:
fc = 1 / 2πT
其中 T 是以秒為單位的時間常數。
這種類型的濾波器的工作效率的特點是它們的截止頻率和伏特(輸入)/伏特(輸出)比開始下降到截止頻率閾值以上的速率。
后者通常表示為每倍頻程(每加倍一個頻率)的(一些)dB,如下圖所示,它顯示了dB與伏特(輸入)/伏特(輸出)比之間的關系,并且還提供了準確的頻率響應曲線。

RC 低通濾波器
顧名思義,低通濾波器設計用于在截止頻率以下傳輸交流信號,同時將信號強度的損耗或衰減降至最低。對于高于截止頻率的信號,低通濾波器會產生更大的衰減。

可以計算這些濾波器的確切組件值。例如,可以構建放大器中常用的標準劃痕濾波器,以衰減超過10 kHz的頻率。此特定值表示濾波器的預期截止頻率。
RC 高通濾波器
高通濾波器設計為以相反的方式工作。它們衰減低于截止頻率的頻率,但允許所有頻率等于或高于設定截止頻率,而不會衰減。
為了實現這種高通濾波器實現,電路中的RC元件只需相互交換,如下所示。

高通濾波器類似于其低通對應物。這些通常用于放大器和音頻設備,以消除固有的,不需要的低頻產生的噪聲或“隆隆聲”。
要消除的選定截止頻率應足夠低,以免與“良好”低音響應沖突。因此,確定的幅度通常在 15 到 20 Hz 的范圍內。
計算RC截止頻率
確切地說,計算此截止頻率需要相同的公式,因此,以20 Hz作為截止閾值,我們有:
20 = 1 / 2 x 3.14 x RC
RC = 125。
這表明,只要選擇RC網絡,使其乘積為125,就可以在20 Hz信號以下實現預期的高通截止。
在實際電路中,這種濾波器通常在前置放大器級引入,或者在放大器中緊接在現有音調控制電路之前引入。
對于Hi-Fi器件,這些截止濾波電路通常比這里解釋的要復雜得多,以使截止點具有更高的效率和引腳點精度。
-
電容器
+關注
關注
64文章
6208瀏覽量
99335 -
電阻
+關注
關注
86文章
5476瀏覽量
171698 -
RC電路
+關注
關注
2文章
161瀏覽量
30196
發布評論請先 登錄
相關推薦
RC電路簡介,RC串并聯電路的工作原理及應用




 深度剖析RC電路的工作原理
深度剖析RC電路的工作原理











評論