我們現在知道，「通電」代表「真」，用邏輯1表示；「不通電」代表「假」，用邏輯0表示。「與門」電路是用晶體管搭建的，符號長這樣：

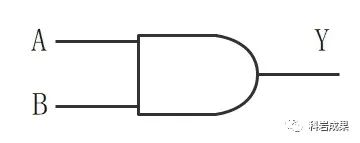
A與B的通斷，可以決定Y點是否通電。

我們還為A、B與Y之間的關系畫了一張表（真值表）：

接著我們設計出了簡單的「或門」「非門」，用它們可以搭建各式各樣其他的門電路。

這篇文章講一下，怎么利用基礎門電路進行加法計算。

二進制加法

我已經忘了是什么時候學的加法了，應該是小學吧，先學10以內的，再學100以內的，然后不管多大的數都可以隨便加了，算式很簡單，就是逢10進1。

下面這個式子是一個萬以內的加法：

相應的，二進制就是逢2進1，下面這個式子是2個8位二進制數的加法計算：

半加器

8位二進制數還太復雜，我們先來看看1位二進制數怎么計算的，一共有以下4種情況：

觀察一下就能發現2個規律。

第一個規律，只考慮加法，不考慮進位時，加數與和之間的關系如下：

相同為0，不同為1。這個關系和「異或門」是相同的：

異或門我們之前沒有聊到過，電路圖長這樣：

第二個規律是，如果只考慮進位，不考慮加法，加數與進位之間的關系如下：

只有全1時，才為1。發現了嗎，這和本文開頭與門的真值表是一樣的。

2個一位二進制數相加將產生一個加法位和一個進位位，加法位輸入與輸出的關系跟與門是一樣的，進位位跟異或門相同。

所以，可以像這樣把兩個門電路連起來，計算2個二進制數（A和B）的和：

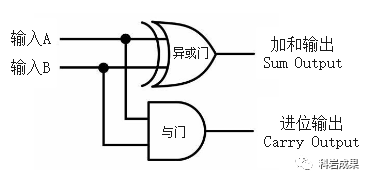
我們稱這個電路為「半加器」，因為它只能計算2個一位二進制數的加法，沒有辦法將前面加法可能產生的進位納入下一次計算中，如果有進位則實際上是需要3個加數參與計算。

用門電路畫太復雜，可以封裝起來這樣表示半加器：

全加器

怎樣計算3個加數的二進制加法呢？需要將2個半加器和一個或門如圖連接起來：

左邊能看到它有3個輸入，右邊依舊是1位加和輸出，1位進位輸出。

2個數的加和與上一次的進位相加，得出的加和作為3個數最終的加和；2個數相加或3個數相加的進位作為3個數加和最終的進位位。

用文字描述有點不好理解，把這個電路圖全部輸入和輸出情況都展示出來，畫一個表就明白了：

很明顯，這個表就是2個一位二進制數帶進位的全部狀態。

每次做加法時畫2個半加器和一個或門很麻煩，我們用下面這個圖示把它們封裝起來，這個能計算3位二進制數加法的電路就稱為「全加器」。

加法器

現在回到開頭那個二進制加法：

它有8個二進制位，到目前為止我們還只能計算2個一位二進制數，最多再增加一個進位的加法，我們最終的目標當然是2個8位、16位乃至32位數的加法。

其實，非常簡單，用8個全加器一塊算！

把8個全加器每個進位輸出作為下一個的進位輸入，首尾相連就可以啦！

每次這樣畫太麻煩，可以封裝成一個框圖：

大箭頭代表8個輸入/輸出端，有8個獨立的信號。

一旦我們擁有了8位二進制加法器，把它們級聯起來，很容易就能得到一個16位或32位的加法器啦。

end

加法計算是計算機的基本運算，其實，計算機唯一的工作就是做加法計算。 不論是減法、乘法、除法、在線支付、火箭升空還是AI下棋，都是利用加法實現的。

把加減乘除和邏輯運算等運算單元集成起來，就組成了CPU中的基本計算單元：ALU（算術邏輯單元Arithmetic and Logic Unit）。

用加法器計算2個數的加法其實就是用硬件方式實現了一個加法計算器，輸入A和輸入B的高低電平決定了輸出S和CO的高低電平。

這樣的電路同一時刻只能表示一種狀態，只要改變了A、B中任意一位，輸出就會有所變化。

現在我們想計算更多二進制數的加法，比如5個數A、B、C、D、E的加法（先不考慮進位）。

步驟應該是這樣：首先把A、B作為輸入，得出一個輸出S1，我們要記下來S1的值，然后把S1和C作為輸入，得出S2....以此類推，要記下很多個數，然后再用加法器計算。

5個數都已經很麻煩了，如果要計算更多個數該怎么辦？能不能把每次計算完的結果存起來，下次繼續使用呢？