前言
之前的一次推送介紹了Mahony姿態(tài)解算算法(IMU姿態(tài)濾波算法——Mahony算法:原理與代碼),這次介紹另一個(gè)經(jīng)典的濾波算法:Madgwick濾波。
Madgwick濾波算法根據(jù)加速度計(jì)、陀螺儀、以及磁力計(jì),融合計(jì)算機(jī)體四元數(shù),計(jì)算速度快、精度較高。本文詳細(xì)介紹六軸融合,即根據(jù)加速度計(jì)和陀螺儀數(shù)據(jù),計(jì)算IMU的姿態(tài)。
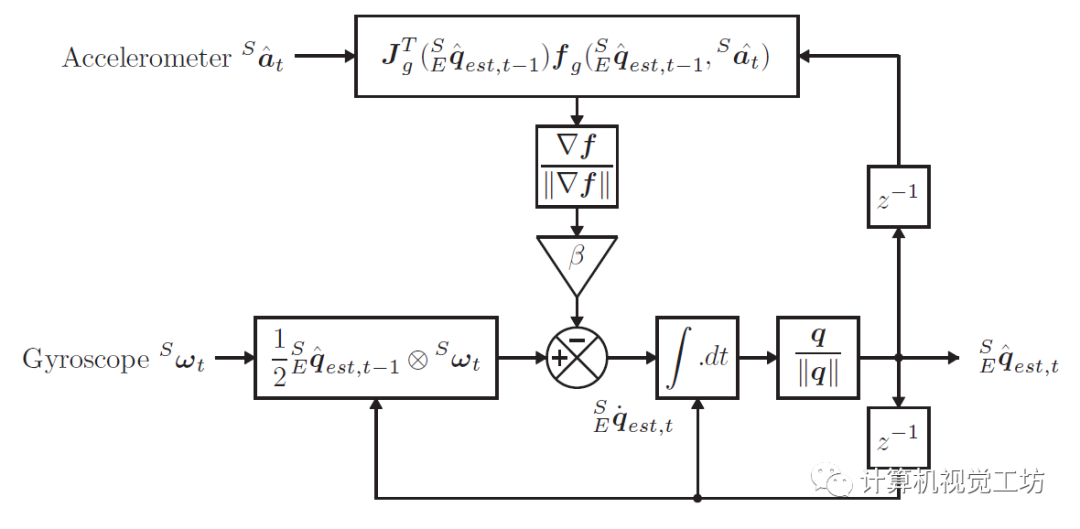
算法
2.1 重力方向?qū)R優(yōu)化
首先要指出的是,Madgwick算法假設(shè)加速度計(jì)測(cè)量的加速度完全由重力提供,即物體本體運(yùn)動(dòng)產(chǎn)生的加速度可忽略不計(jì)。這一點(diǎn)和Mahony算法是一樣的。
假設(shè)world系中一個(gè)向量在world下的表示為 ,在傳感器下的觀測(cè)為 ,傳感器位姿以四元數(shù)表示記為 。如果此時(shí)的姿態(tài)是準(zhǔn)確的,應(yīng)該有:
然而由于姿態(tài)不準(zhǔn),等式并不成立。因此,我們定義目標(biāo)函數(shù):
令目標(biāo)函數(shù)取到0(在四元數(shù)對(duì)應(yīng)的參數(shù)空間上),則得到了最優(yōu)的姿態(tài),即。這可以當(dāng)作一個(gè)優(yōu)化問題進(jìn)行求解。而優(yōu)化問題的求解思路之一,就是采用梯度下降法。記的梯度為,那么在迭代優(yōu)化求解時(shí),下一次取值應(yīng)該為當(dāng)前取值減去當(dāng)前梯度方向走一個(gè)步長(zhǎng),即
其中,
其中, 為 的雅可比(具體的形式可參考文獻(xiàn)[1][2])。
可以將步長(zhǎng) 視作加速度計(jì)產(chǎn)生的數(shù)據(jù)對(duì)姿態(tài)的收斂速度,同時(shí)考慮到角速度在當(dāng)前時(shí)刻會(huì)產(chǎn)生一個(gè)角速度的增量,因此加速度這部分的收斂必須大于角速度變化速率,即 ,其中 。
對(duì)于一般的優(yōu)化,我們需要不斷迭代求解直到收斂,但Madgwick為了保證算法的實(shí)時(shí)性,只進(jìn)行一次梯度下降,也能取得差不多的精度。
具體地,如果我們把world系下的這個(gè)向量 取重力 ,姿態(tài)傳感器對(duì)應(yīng)的測(cè)量 即為IMU的加速度計(jì)讀數(shù) ,此時(shí)有:
2.2 角速度融合
另一方面,我們可以通過角速度計(jì)提供的角速度積分,得到姿態(tài),即:
這里我們對(duì)四元數(shù)進(jìn)一步的區(qū)分。我們對(duì)上一時(shí)刻濾波后的姿態(tài)(四元數(shù))記為 ,當(dāng)前時(shí)刻角速度計(jì)的讀數(shù)即角速度為 ,角速度計(jì)計(jì)算得到的姿態(tài)為 。
對(duì)2.1中優(yōu)化后得到的四元數(shù)記為 ,即加速度計(jì)計(jì)算得到的姿態(tài)。
那么,當(dāng)前時(shí)刻估計(jì)的姿態(tài)取做兩個(gè)姿態(tài)的加權(quán)平均:
至于 如何取值,下一小節(jié)進(jìn)行討論。
2.3 權(quán)重取值
由于角速度存在漂移,我們定義角速度的發(fā)散速率為 。這里如果加速度計(jì)對(duì)姿態(tài)貢獻(xiàn)的收斂速度,等于角速度的發(fā)散速度,則由式(5)融合的結(jié)果依舊是準(zhǔn)確的姿態(tài)。即需要有:
即
由于 中對(duì) 沒有限制,因此取 為無限大,此時(shí),綜合(1)(5)(6),有:
定義估計(jì)的角速度 ,則最終有:
再看式(7),可以將視作,下一時(shí)刻的姿態(tài),等于上一時(shí)刻姿態(tài),加上角速度計(jì)的積分,減去一個(gè)與角速度計(jì)噪聲水平 相關(guān)的增量,這個(gè)增量的與加速度計(jì)的優(yōu)化時(shí)的梯度有關(guān)。最終,Madgwick濾波算法的參數(shù)只有一個(gè)。
代碼
Matlab完整代碼[3]如下:
functionobj=UpdateIMU(obj,Gyroscope,Accelerometer)
q=obj.Quaternion; if(norm(Accelerometer)==0),return;end Accelerometer=Accelerometer/norm(Accelerometer);%歸一化加速度計(jì)數(shù)據(jù) %式(2)和(3) F=[2*(q(2)*q(4)-q(1)*q(3))-Accelerometer(1) 2*(q(1)*q(2)+q(3)*q(4))-Accelerometer(2) 2*(0.5-q(2)^2-q(3)^2)-Accelerometer(3)]; J=[-2*q(3),2*q(4),-2*q(1),2*q(2) 2*q(2),2*q(1),2*q(4),2*q(3) 0,-4*q(2),-4*q(3),0]; step=(J'*F); step=step/norm(step);%式(1)中的減號(hào)后面的部分,即修正量 %式(8)中的修正角速度 qDot=0.5*quaternProd(q,[0Gyroscope(1)Gyroscope(2)Gyroscope(3)])-obj.Beta*step'; %式(7)(8),即迭代到下一步。 q=q+qDot*obj.SamplePeriod; obj.Quaternion=q/norm(q);%normalisequaternion end
與Mahony算法的比較
Madgwick算法與Mahony算法相比,最大的不同之處是如何對(duì)待加速度計(jì)估計(jì)的誤差。Mahony是利用叉乘,Madgwick是利用優(yōu)化;
Mahony可以視作一個(gè)PI(比例-積分)控制器,Madgwick是一個(gè)P(比例)控制器;
Madgwick比Mahony的精度稍高一丟丟,但Mahony的計(jì)算速度略快[4];
Mahony與Madgwick都需要假設(shè)加速度測(cè)的只是重力,因此在加速度變化劇烈情況下表現(xiàn)不佳。
編輯:黃飛
-
濾波算法
+關(guān)注
關(guān)注
2文章
88瀏覽量
13708 -
磁力計(jì)
+關(guān)注
關(guān)注
1文章
71瀏覽量
20840
原文標(biāo)題:IMU姿態(tài)濾波算法——Madgwick算法:原理與代碼
文章出處:【微信號(hào):3D視覺工坊,微信公眾號(hào):3D視覺工坊】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
基于LMS算法與RLS算法的自適應(yīng)濾波
基于無源定位的粒子濾波算法
濾波算法有哪些十大濾波算法的資料介紹

如何使用FPGA實(shí)現(xiàn)圖像的中值濾波算法
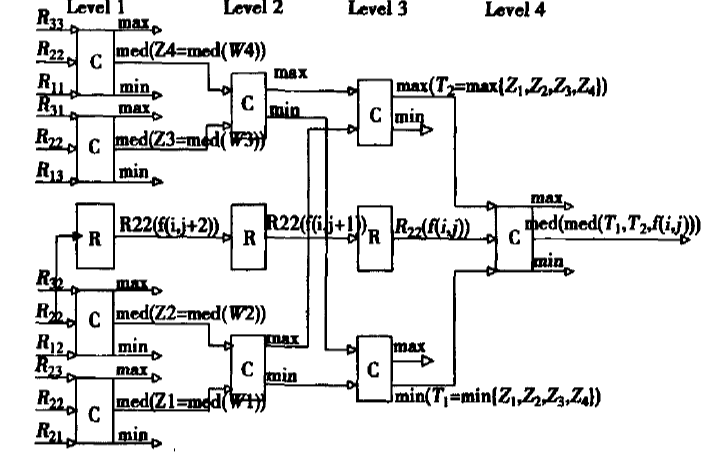




 經(jīng)典的濾波算法:Madgwick濾波算法
經(jīng)典的濾波算法:Madgwick濾波算法










評(píng)論