積分梳狀濾波器（CIC，Cascaded Integrator Comb），一般用于數字下變頻（DDC）和數字上變頻（DUC）系統。CIC 濾波器結構簡單，沒有乘法器，只有加法器、積分器和寄存器，資源消耗少，運算速率高，可實現高速濾波，常用在輸入采樣率最高的第一級，在多速率信號處理系統中具有著廣泛應用。

DDC 原理

◆DDC 工作原理

DDC 主要由本地振蕩器（NCO） 、混頻器、濾波器等組成，如下圖所示。

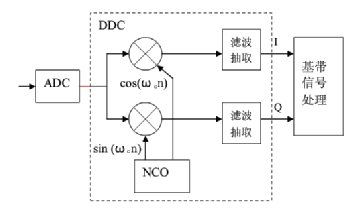
DDC 將中頻信號與振蕩器產生的載波信號進行混頻，信號中心頻率被搬移，再經過抽取濾波，恢復原始信號，實現了下變頻功能。

中頻數據采樣時，需要很高的采樣頻率來確保 ADC（模數轉換器）采集到信號的信噪比。經過數字下變頻后，得到的基帶信號采樣頻率仍然是 ADC 采樣頻率，所以數據率很高。此時基帶信號的有效帶寬往往已經遠小于采樣頻率，所以利用抽取、濾波進行數據速率的轉換，使采樣率降低，避免資源的浪費和設計的困難，就成為 DDC 不可缺少的一部分。

而采用 CIC 濾波器進行數據處理，是 DDC 抽取濾波部分最常用的方法。

◆帶通采樣定理

在 DDC 系統中，輸入的中頻載波信號會根據載波頻率進行頻移，得到一個帶通信號。如果此時仍然采用奈奎斯特采樣定理，即采樣頻率為帶通信號最高頻率的兩倍，那么此時所需的采樣頻率將會很高，設計會變的復雜。此時可按照帶通采樣定理來確定抽樣頻率。

帶通采樣定理：一個頻帶限制在的連續帶通信號，帶寬為。令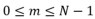 ，其中 N 為不大于的最大正整數，如果采樣頻率滿足條件：

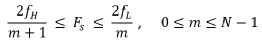
則該信號完全可以由其采樣值無失真的重建。

當 m=1 時，帶通采樣定理便是奈奎斯特采樣定理。

帶通采樣定理的另一種描述方式為：若信號最高頻率為信號帶寬的整數倍，采樣頻率只需大于信號帶寬的兩倍即可，此時不會發生頻譜混疊。

所以，可以認為采樣頻率的一半是 CIC 濾波器的截止頻率。

◆DDC 頻譜搬移

例如一個帶寬信號中心頻率為 60MHz，帶寬為 8MHz, 則頻率范圍為 56MHz ~ 64MHz，m 的可取值范圍為 0 ~ 7。取 m=1, 則采樣頻率范圍為 64MHz ~ 112MHz。

取采樣頻率為 80MHz，設 NCO 中心頻率為 20 MHz，下面討論復信號頻譜搬移示意圖。

（1）考慮頻譜的對稱性，輸入復信號的頻譜示意圖如下：

（2）80MHz 采樣頻率采樣后，5664MHz 的頻帶被搬移到了 -24 -16MHz 與 136 ~ 144MHz（高于采樣頻率被濾除）的頻帶處，-64~ -56MHz 的頻帶被搬移到 -144~ -136MHz（高于采樣頻率被濾除）與 16~24MHz 的頻帶處。

采樣后頻帶分布如下：

（3）信號經過 20MHz NCO 的正交電路后， -24~ -16MHz 的頻帶被搬移到 -44MHz 與 -44 -36MHz 的頻帶處，1624MHz 的頻帶被搬移到 -44MHz 與 36~44MHz 的頻帶處，如下所示。

（4）此時中頻輸入的信號已經被搬移到零中頻基帶處。

-44~ -36MHz 和 3644MHz 的帶寬信號是不需要的，可以濾除；-44MHz 的零中頻信號數據速率仍然是 80MHz，可以進行抽取降低數據速率。而 CIC 濾波，就是要完成這個過程。

上述復習了很多數字信號處理的內容，權當拋 DDC 的磚，引 CIC 的玉。

CIC 濾波器原理

◆單級 CIC 濾波器

設濾波器抽取倍數為 D，則單級濾波器的沖激響應為：

對其進行 z 變換，可得單級 CIC 濾波器的系統函數為：

令

可以看出，單級 CIC 濾波器包括兩個基本組成部分：積分部分和梳狀部分，結構圖如下：

◆積分器

積分器是一個單級點的 IIR（Infinite Impulse Response，無限長脈沖沖激響應）濾波器，且反饋系數為 1，其狀態方程和系統函數分別為：

◆梳狀器

梳狀器是一個 FIR 濾波器，其狀態方程和系統函數分別為：

◆抽取器

在積分器之后，還有一個抽取器，抽取倍數與梳狀器的延時參數是一致的。利用 z 變換的性質進行恒等變換，將抽取器移動到積分器與梳狀器之間，可得到單級 CIC 濾波器結構，如下所示。

◆參數說明

CIC 濾波器結構變換之前的參數 D 可以理解為梳狀濾波器的延時或階數；變換之后，D 的含義 變為抽取倍數，而此時梳狀濾波器的延時為 1，即階數為 1。

很多學者會引入一個變量 M，表示梳狀器每一級的延時，此時梳妝部分的延時就不為 1 了。那么梳狀器的系統函數就變為：

其實把 DM 整體理解為單級濾波器延時，或者抽取倍數，也都是可以的。可能實現的方式或結構不同，但是最后的結果都是一樣的。本次設計中，單級濾波器延時都為 M=1，即抽取倍數與濾波延時相同。

◆多級 CIC 濾波器

單級 CIC 濾波器的阻帶衰減較差，為了提高濾波效果，抽取濾波時往往會采用多級 CIC 濾波器級聯的結構。

實現多級直接級聯的 CIC 濾波器在設計和資源上并不是最優的方式，需要對其結構進行調整。如下所示，將積分器和梳狀濾波器分別移至一組，并將抽取器移到梳狀濾波器之前。先抽取再進行濾波，可以減少數據處理的長度，節約硬件資源。

當然，級聯數越大，旁瓣抑制越好，但是通帶內的平坦度也會變差。所以級聯數不宜過多，一般最多 5 級。

CIC 濾波器設計

◆設計說明

CIC 濾波器本質上就是一個簡單的低通濾波器，截止頻率為采樣頻率除以抽取倍數后的一半。輸入數據信號仍然是 7.5MHz 和 250KHz，采樣頻率 50MHz。抽取倍數設置為 5，則截止頻率為 5MHz，小于 7.5MHz，可以濾除 7.5MHz 的頻率成分。設計參數如下：

輸入頻率： 7.5MHz 和 250KHz

采樣頻率： 50MHz

阻帶： 5MHz

階數： 1（M=1）

級數： 3（N=3）

關于積分時中間數據信號的位寬，很多地方給出了不同的計算方式，計算結果也大相徑庭。這里總結一下使用最多的計算方式：

其中，D 為抽取倍數，M 為濾波器階數，N 為濾波器級數。抽取倍數為 5，濾波器階數為 1，濾波器級聯數為 3，取輸入信號數據位寬為 12bit，對數部分向上取整，則積分后數據不溢出的中間信號位寬為 21bit。

為了更加寬裕的設計，濾波器階數如果理解為未變換結構前的多級 CIC 濾波器直接型結構，則濾波器階數可以認為是 5，此時中間信號最大位寬為 27bit。

◆積分器設計

根據輸入數據的有效信號的控制，積分器做一個簡單的累加即可，注意數據位寬。

//3 stages integrator
module integrator
    #(parameter NIN     = 12,
      parameter NOUT    = 21)
    (
      input               clk ,
      input               rstn ,
      input               en ,
      input [NIN-1:0]     din ,
      output              valid ,
      output [NOUT-1:0]   dout) ;


    reg [NOUT-1:0]         int_d0  ;
    reg [NOUT-1:0]         int_d1  ;
    reg [NOUT-1:0]         int_d2  ;
    wire [NOUT-1:0]        sxtx = {{(NOUT-NIN){1'b0}}, din} ;


    //data input enable delay
    reg [2:0]              en_r ;
    always @(posedge clk or negedge rstn) begin
        if (!rstn) begin
            en_r   <= 'b0 ;
        end
        else begin
            en_r   <= {en_r[1:0], en};
        end
    end


    //integrator
    //stage1
    always @(posedge clk or negedge rstn) begin
        if (!rstn) begin
            int_d0        <= 'b0 ;
        end
        else if (en) begin
            int_d0        <= int_d0 + sxtx ;
        end
    end


    //stage2
    always @(posedge clk or negedge rstn) begin
        if (!rstn) begin
            int_d1        <= 'b0 ;
        end
        else if (en_r[0]) begin
            int_d1        <= int_d1 + int_d0 ;
        end
    end


   //stage3
    always @(posedge clk or negedge rstn) begin
        if (!rstn) begin
            int_d2        <= 'b0 ;
        end
        else if (en_r[1]) begin
            int_d2        <= int_d2 + int_d1 ;
        end
    end
    assign dout  = int_d2 ;
    assign valid = en_r[2];


endmodule

◆抽取器設計

抽取器設計時，對積分器輸出的數據進行計數，然后間隔 5 對數據進行抽取即可。

module  decimation
    #(parameter NDEC = 21)
    (
     input                clk,
     input                rstn,
     input                en,
     input [NDEC-1:0]     din,
     output               valid,
     output [NDEC-1:0]    dout);


    reg                  valid_r ;
    reg [2:0]            cnt ;
    reg [NDEC-1:0]       dout_r ;


    //counter
    always @(posedge clk or negedge rstn) begin
        if (!rstn) begin
            cnt <= 3'b0;
        end
        else if (en) begin
            if (cnt==4) begin
                cnt <= 'b0 ;
            end
            else begin
                cnt <= cnt + 1'b1 ;
            end
        end
    end


    //data, valid
    always @(posedge clk or negedge rstn) begin
        if (!rstn) begin
            valid_r        <= 1'b0 ;
            dout_r         <= 'b0 ;
        end
        else if (en) begin
            if (cnt==4) begin
                valid_r     <= 1'b1 ;
                dout_r      <= din;
            end
            else begin
                valid_r     <= 1'b0 ;
            end
        end
    end
    assign dout          = dout_r ;
    assign valid         = valid_r ;


endmodule

◆梳狀器設計

梳狀濾波器就是簡單的一階 FIR 濾波器，每一級的 FIR 濾波器對數據進行一個時鐘延時，然后做相減即可。因為系數為 ±1，所以不需要乘法器。

module comb
    #(parameter NIN  = 21,
      parameter NOUT = 17)
    (
     input               clk,
     input               rstn,
     input               en,
     input [NIN-1:0]     din,
     input               valid,
     output [NOUT-1:0]   dout);


    //en delay
    reg [5:0]                 en_r ;
    always @(posedge clk or negedge rstn) begin
        if (!rstn) begin
            en_r <= 'b0 ;
        end
        else if (en) begin
            en_r <= {en_r[5:0], en} ;
        end
    end

    reg [NOUT-1:0]            d1, d1_d, d2, d2_d, d3, d3_d ;
    //stage 1, as fir filter, shift and add(sub), 
    //no need for multiplier
    always @(posedge clk or negedge rstn) begin
        if (!rstn)        d1     <= 'b0 ;
        else if (en)      d1     <= din ;
    end
    always @(posedge clk or negedge rstn) begin
        if (!rstn)        d1_d   <= 'b0 ;
        else if (en)      d1_d   <= d1 ;
    end
    wire [NOUT-1:0]      s1_out = d1 - d1_d ;


    //stage 2
    always @(posedge clk or negedge rstn) begin
        if (!rstn)        d2     <= 'b0 ;
        else if (en)      d2     <= s1_out ;
    end
    always @(posedge clk or negedge rstn) begin
        if (!rstn)        d2_d   <= 'b0 ;
        else if (en)      d2_d   <= d2 ;
    end
    wire [NOUT-1:0]      s2_out = d2 - d2_d ;


    //stage 3
    always @(posedge clk or negedge rstn) begin
        if (!rstn)        d3     <= 'b0 ;
        else if (en)      d3     <= s2_out ;
    end
    always @(posedge clk or negedge rstn) begin
        if (!rstn)        d3_d   <= 'b0 ;
        else if (en)      d3_d   <= d3 ;
    end
    wire [NOUT-1:0]      s3_out = d3 - d3_d ;


    //tap the output data for better display
    reg [NOUT-1:0]       dout_r ;
    reg                  valid_r ;
    always @(posedge clk or negedge rstn) begin
        if (!rstn) begin
            dout_r         <= 'b0 ;
            valid_r        <= 'b0 ;
        end
        else if (en) begin
            dout_r         <= s3_out ;
            valid_r        <= 1'b1 ;
        end
        else begin
            valid_r        <= 1'b0 ;
        end
    end
    assign       dout    = dout_r ;
    assign       valid   = valid_r ;


endmodule

◆頂層例化

按信號的流向將積分器、抽取器、梳狀器分別例化，即可組成最后的 CIC 濾波器模塊。

梳狀濾波器的最終輸出位寬一般會比輸入信號小一些，這里取 17bit。當然輸出位寬完全可以與輸入數據的位寬一致。

module cic
    #(parameter NIN  = 12,
      parameter NMAX = 21,
      parameter NOUT = 17)
    (
     input               clk,
     input               rstn,
     input               en,
     input [NIN-1:0]     din,
     input               valid,
     output [NOUT-1:0]   dout);


    wire [NMAX-1:0]      itg_out ;
    wire [NMAX-1:0]      dec_out ;
    wire [1:0]           en_r ;


    integrator   #(.NIN(NIN), .NOUT(NMAX))
    u_integrator (
       .clk         (clk),
       .rstn        (rstn),
       .en          (en),
       .din         (din),
       .valid       (en_r[0]),
       .dout        (itg_out));


    decimation   #(.NDEC(NMAX))
    u_decimator (
       .clk         (clk),
       .rstn        (rstn),
       .en          (en_r[0]),
       .din         (itg_out),
       .dout        (dec_out),
       .valid       (en_r[1]));


    comb         #(.NIN(NMAX), .NOUT(NOUT))
    u_comb (
       .clk         (clk),
       .rstn        (rstn),
       .en          (en_r[1]),
       .din         (dec_out),
       .valid       (valid),
       .dout        (dout));


endmodule

◆testbench

testbench 編寫如下，主要功能就是不間斷連續的輸入 250KHz 與 7.5MHz 的正弦波混合信號數據。輸入的混合信號數據也可由 matlab 生成，具體過程參考《并行 FIR 濾波器設計》一節。

module test ;
    parameter    NIN  = 12 ;
    parameter    NMAX = 21 ;
    parameter    NOUT = NMAX ;




    reg                  clk ;
    reg                  rstn ;
    reg                  en ;
    reg  [NIN-1:0]       din ;
    wire                 valid ;
    wire [NOUT-1:0]      dout ;


    //=====================================
    // 50MHz clk generating
    localparam   T50M_HALF    = 10000;
    initial begin
        clk = 1'b0 ;
        forever begin
            # T50M_HALF clk = ~clk ;
        end
    end


    //============================
    //  reset and finish
    initial begin
        rstn = 1'b0 ;
        # 30 ;
        rstn = 1'b1 ;
        # (T50M_HALF * 2 * 2000) ;
        $finish ;
    end


    //=======================================
    // read cos data into register
    parameter    SIN_DATA_NUM = 200 ;
    reg          [NIN-1:0] stimulus [0: SIN_DATA_NUM-1] ;
    integer      i ;
    initial begin
        $readmemh("../tb/cosx0p25m7p5m12bit.txt", stimulus) ;
        i         = 0 ;
        en        = 0 ;
        din       = 0 ;
        # 200 ;
        forever begin
            @(negedge clk) begin
                en          = 1 ;
                din         = stimulus[i] ;
                if (i == SIN_DATA_NUM-1) begin
                    i = 0 ;
                end
                else begin
                    i = i + 1 ;
                end
            end
        end
    end


    cic #(.NIN(NIN), .NMAX(NMAX), .NOUT(NOUT))
    u_cic (
     .clk         (clk),
     .rstn        (rstn),
     .en          (en),
     .din         (din),
     .valid       (valid),
     .dout        (dout));


endmodule

◆仿真結果

由下圖仿真結果可知，經過 CIC 濾波器后的信號只有一種低頻率信號（250KHz），高頻信號（7.5MHz）被濾除了。

但是波形不是非常完美，這與設計的截止頻率、數據不是持續輸出等有一定關系。

此時發現，積分器輸出的數據信號也非常的不規則，這與其位寬有關系。

為了更好的觀察積分器輸出的數據，將其位寬由 21bit 改為 34bit，仿真結果如下。

此時發現，CIC 濾波器的數據輸出并沒有實質性的變化，但是積分器輸出的數據信號呈現鋸齒狀，也稱之為梳狀。這也是梳狀濾波器名字的由來。