一、支持向量機的求解過程
個人理解:下文所有下標i、j均可相互替換,c和C表示同一常數。
支持向量機的對偶問題為: 最大化:θ(α,β)=∑αi-1/2∑∑yiyjαiαjφ(Xi)Tφ(Xj);
限制條件:(1)0≤αi≤C,i=1~N;(2)∑αiyi=0,i=1~N。
因為φ(Xi)Tφ(Xj)=K(Xi,Xj)(K(Xi,Xj)為核函數,詳見),所以只需知道核函數K(Xi,Xj)即可求解該對偶問題。該對偶問題解的結構為一組αi的值(個人理解:αi的值同時也為αj的值),其中i=1~N。
解得αi的值后可根據ω=∑αiyiφ(Xi)求解ω的值(支持向量機問題需解得超平面ωTφ(X)+b=0中的ω和b的值),但因為φ(Xi)不一定具有顯式表達式,所以ω不一定具有顯式表達式。
雖然ω不一定具有顯式表達式,但ωTφ(X)+b的形式可以通過核函數K(X1,X2)求得,下文介紹具體求解過程:
因為ω=∑αjyjφ(Xj),所以ωTφ(Xj)=∑αjyjφ(Xj)Tφ(Xi)=∑αjyjK(Xj,Xi)。
根據KKT條件(KKT條件見機器學習相關介紹(12)——支持向量機(原問題和對偶問題)),且持向量機的對偶問題的另一個形式為: 最大化:θ(α,β)=inf{1/2||ω||2-C∑βiδi+∑αi[1+δi-yiωTφ(Xi)-yib]}; 限制條件:(1)αi≥0,i=1~N;(2)βi≥0,i=1~N。
可得:對所有的i=1~N,βiδi=0且αi[1+δi-yiωTφ(Xi)-yib]=0。
根據βiδi=0可得(c-αi)δi=0(個人理解:此步驟也需根據機器學習相關介紹(13)——支持向量機(轉化為對偶問題)中求偏導得出的等式αi+βi=C)
若對某個i,αi≠0且αi≠c,則根據KKT條件,則有δi=0且1+δi-yiωTφ(Xi)-yib=0。
又因為yiωTφ(Xi)=∑αiyjyiK(Xj,Xi),所以只需使用一個滿足0<αi<c的αi值,即可通過下式求得b: b=(1-∑αjyjyiK(Xj,Xi))/yi
綜上,ωTφ(X)+b=∑αiyiK(Xi,X)+b,即在不知道φ(X),只知道K(X1,X2)的情況下,ωTφ(X)+b的表達式也可被求出。該結論被稱為“核函數戲法”(KERNEL TRICK)。
最終,支持向量機的判別標準為: 若∑αiyiK(Xi,X)+b≥0,則X∈C1; 若∑αiyiK(Xi,X)+b<0,則X∈C2。
二、支持向量機的算法流程
(1)訓練過程
輸入訓練數據{(Xi,yi)},i=1~N,其中,yi=±1。并求解: 最大化:θ(α,β)=∑αi-1/2∑∑yiyjαiαjφ(Xi)Tφ(Xj);
限制條件:
(1)0≤αi≤C,i=1~N;(2)∑αiyi=0,i=1~N。
得出一組αi的值,再通過一個滿足0<αi<c的αi值,根據下式求b: b=(1-∑αjyjyiK(Xj,Xi))/yi
求解出αi和b后,支持向量機的訓練過程完成。
(2)測試過程
考察測試數據X,預測其類別y: 若∑αiyiK(Xi,X)+b≥0,則y=+1(X∈C1); 若∑αiyiK(Xi,X)+b<0,則y=-1(X∈C2)。
審核編輯:劉清
-
向量機
+關注
關注
0文章
166瀏覽量
20856 -
機器學習
+關注
關注
66文章
8381瀏覽量
132428
原文標題:機器學習相關介紹(14)——支持向量機(算法流程)
文章出處:【微信號:行業學習與研究,微信公眾號:行業學習與研究】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于改進支持向量機的貨幣識別研究
基于支持向量機(SVM)的工業過程辨識
基于標準支持向量機的陣列波束優化及實現
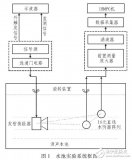
模糊支持向量機的改進方法
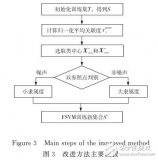
多分類孿生支持向量機研究進展
支持向量機的故障預測模型
如何從零推導支持向量機
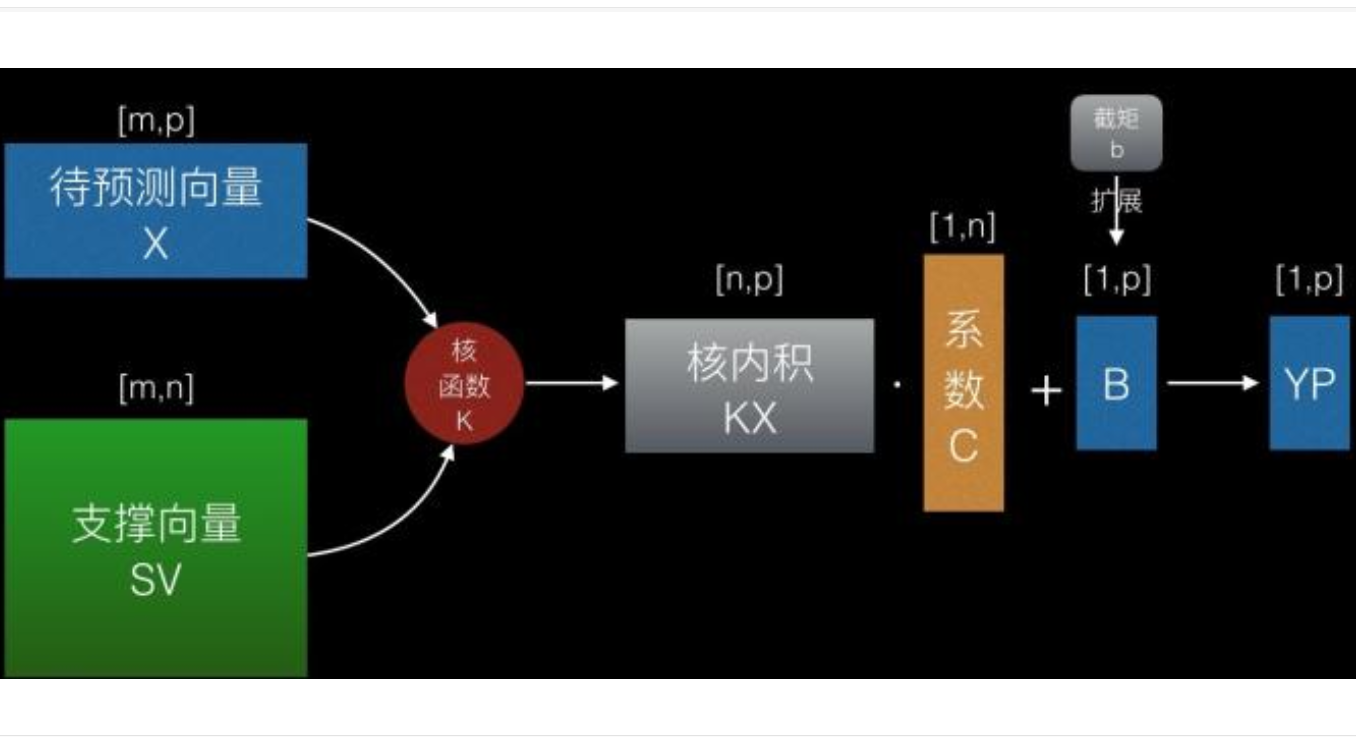
什么是支持向量機 什么是支持向量
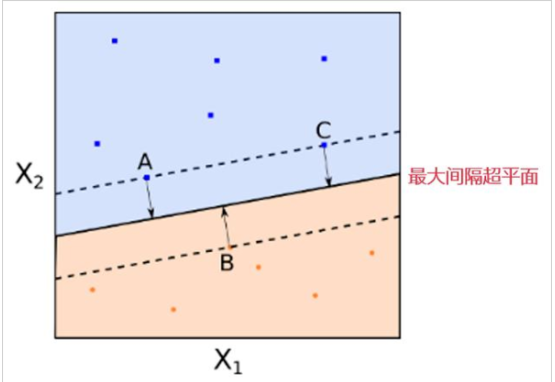




 支持向量機的求解過程
支持向量機的求解過程
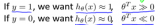
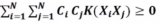










評論