我們在16.4 節介紹了自然語言推理任務和 SNLI 數據集。鑒于許多基于復雜和深層架構的模型， Parikh等人。( 2016 )提出用注意力機制解決自然語言推理，并將其稱為“可分解注意力模型”。這導致模型沒有循環層或卷積層，在 SNLI 數據集上以更少的參數獲得了當時最好的結果。在本節中，我們將描述和實現這種用于自然語言推理的基于注意力的方法（使用 MLP），如圖 16.5.1所示。

圖 16.5.1本節將預訓練的 GloVe 提供給基于注意力和 MLP 的架構以進行自然語言推理。

16.5.1。該模型

比保留前提和假設中標記的順序更簡單的是，我們可以將一個文本序列中的標記與另一個文本序列中的每個標記對齊，反之亦然，然后比較和聚合這些信息以預測前提和假設之間的邏輯關系。類似于機器翻譯中源句和目標句之間的 token 對齊，前提和假設之間的 token 對齊可以通過注意力機制巧妙地完成。

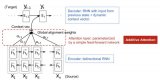
圖 16.5.2使用注意機制的自然語言推理。

圖 16.5.2描述了使用注意機制的自然語言推理方法。在高層次上，它由三個聯合訓練的步驟組成：參與、比較和聚合。我們將在下面逐步說明它們。

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

from mxnet import gluon, init, np, npx
from mxnet.gluon import nn
from d2l import mxnet as d2l

npx.set_np()

16.5.1.1。出席

第一步是將一個文本序列中的標記與另一個序列中的每個標記對齊。假設前提是“我確實需要睡覺”，假設是“我累了”。由于語義相似，我們可能希望將假設中的“i”與前提中的“i”對齊，并將假設中的“tired”與前提中的“sleep”對齊。同樣，我們可能希望將前提中的“i”與假設中的“i”對齊，并將前提中的“需要”和“睡眠”與假設中的“疲倦”對齊。請注意，使用加權平均的這種對齊是軟的，其中理想情況下較大的權重與要對齊的標記相關聯。為了便于演示，圖 16.5.2以硬方式顯示了這種對齊方式 。

現在我們更詳細地描述使用注意機制的軟對齊。表示為 A=(a1,…,am)和 B=(b1,…,bn)前提和假設，其標記數為m和n，分別在哪里 ai,bj∈Rd (i=1,…,m,j=1,…,n) 是一個d維詞向量。對于軟對齊，我們計算注意力權重 eij∈R作為

(16.5.1)eij=f(ai)?f(bj),

哪里的功能f是在以下函數中定義的 MLP mlp 。的輸出維度fnum_hiddens由的參數指定 mlp。

def mlp(num_inputs, num_hiddens, flatten):
  net = []
  net.append(nn.Dropout(0.2))
  net.append(nn.Linear(num_inputs, num_hiddens))
  net.append(nn.ReLU())
  if flatten:
    net.append(nn.Flatten(start_dim=1))
  net.append(nn.Dropout(0.2))
  net.append(nn.Linear(num_hiddens, num_hiddens))
  net.append(nn.ReLU())
  if flatten:
    net.append(nn.Flatten(start_dim=1))
  return nn.Sequential(*net)

def mlp(num_hiddens, flatten):
  net = nn.Sequential()
  net.add(nn.Dropout(0.2))
  net.add(nn.Dense(num_hiddens, activation='relu', flatten=flatten))
  net.add(nn.Dropout(0.2))
  net.add(nn.Dense(num_hiddens, activation='relu', flatten=flatten))
  return net

需要強調的是，在(16.5.1) f接受輸入ai和bj分開而不是將它們中的一對一起作為輸入。這種分解技巧只會導致m+n的應用（線性復雜度） f而不是mn應用程序（二次復雜度）。

對(16.5.1)中的注意力權重進行歸一化，我們計算假設中所有標記向量的加權平均值，以獲得與由索引的標記軟對齊的假設表示i在前提下：

(16.5.2)βi=∑j=1nexp?(eij)∑k=1nexp?(eik)bj.

同樣，我們為由索引的每個標記計算前提標記的軟對齊j在假設中：

(16.5.3)αj=∑i=1mexp?(eij)∑k=1mexp?(ekj)ai.

下面我們定義Attend類來計算假設 ( beta) 與輸入前提的軟對齊A以及前提 ( alpha) 與輸入假設的軟對齊B。

class Attend(nn.Module):
  def __init__(self, num_inputs, num_hiddens, **kwargs):
    super(Attend, self).__init__(**kwargs)
    self.f = mlp(num_inputs, num_hiddens, flatten=False)

  def forward(self, A, B):
    # Shape of `A`/`B`: (`batch_size`, no. of tokens in sequence A/B,
    # `embed_size`)
    # Shape of `f_A`/`f_B`: (`batch_size`, no. of tokens in sequence A/B,
    # `num_hiddens`)
    f_A = self.f(A)
    f_B = self.f(B)
    # Shape of `e`: (`batch_size`, no. of tokens in sequence A,
    # no. of tokens in sequence B)
    e = torch.bmm(f_A, f_B.permute(0, 2, 1))
    # Shape of `beta`: (`batch_size`, no. of tokens in sequence A,
    # `embed_size`), where sequence B is softly aligned with each token
    # (axis 1 of `beta`) in sequence A
    beta = torch.bmm(F.softmax(e, dim=-1), B)
    # Shape of `alpha`: (`batch_size`, no. of tokens in sequence B,
    # `embed_size`), where sequence A is softly aligned with each token
    # (axis 1 of `alpha`) in sequence B
    alpha = torch.bmm(F.softmax(e.permute(0, 2, 1), dim=-1), A)
    return beta, alpha

class Attend(nn.Block):
  def __init__(self, num_hiddens, **kwargs):
    super(Attend, self).__init__(**kwargs)
    self.f = mlp(num_hiddens=num_hiddens, flatten=False)

  def forward(self, A, B):
    # Shape of `A`/`B`: (b`atch_size`, no. of tokens in sequence A/B,
    # `embed_size`)
    # Shape of `f_A`/`f_B`: (`batch_size`, no. of tokens in sequence A/B,
    # `num_hiddens`)
    f_A = self.f(A)
    f_B = self.f(B)
    # Shape of `e`: (`batch_size`, no. of tokens in sequence A,
    # no. of tokens in sequence B)
    e = npx.batch_dot(f_A, f_B, transpose_b=True)
    # Shape of `beta`: (`batch_size`, no. of tokens in sequence A,
    # `embed_size`), where sequence B is softly aligned with each token
    # (axis 1 of `beta`) in sequence A
    beta = npx.batch_dot(npx.softmax(e), B)
    # Shape of `alpha`: (`batch_size`, no. of tokens in sequence B,
    # `embed_size`), where sequence A is softly aligned with each token
    # (axis 1 of `alpha`) in sequence B
    alpha = npx.batch_dot(npx.softmax(e.transpose(0, 2, 1)), A)
    return beta, alpha

16.5.1.2。比較

在下一步中，我們將一個序列中的標記與與該標記軟對齊的另一個序列進行比較。請注意，在軟對齊中，來自一個序列的所有標記，盡管可能具有不同的注意力權重，但將與另一個序列中的標記進行比較。為了便于演示，圖 16.5.2以硬方式將令牌與對齊令牌配對。例如，假設參與步驟確定前提中的“need”和“sleep”都與假設中的“tired”對齊，則將比較“tired-need sleep”對。

在比較步驟中，我們提供連接（運算符 [?,?]) 來自一個序列的標記和來自另一個序列的對齊標記到一個函數中g（一個 MLP）：

(16.5.4)vA,i=g([ai,βi]),i=1,…,mvB,j=g([bj,αj]),j=1,…,n.

在(16.5.4)中，vA,i是token之間的比較i在前提和所有與 token 軟對齊的假設 tokeni; 盡管 vB,j是token之間的比較j在假設和所有與標記軟對齊的前提標記中j. 下面的Compare類定義了比較步驟。

class Compare(nn.Module):
  def __init__(self, num_inputs, num_hiddens, **kwargs):
    super(Compare, self).__init__(**kwargs)
    self.g = mlp(num_inputs, num_hiddens, flatten=False)

  def forward(self, A, B, beta, alpha):
    V_A = self.g(torch.cat([A, beta], dim=2))
    V_B = self.g(torch.cat([B, alpha], dim=2))
    return V_A, V_B

class Compare(nn.Block):
  def __init__(self, num_hiddens, **kwargs):
    super(Compare, self).__init__(**kwargs)
    self.g = mlp(num_hiddens=num_hiddens, flatten=False)

  def forward(self, A, B, beta, alpha):
    V_A = self.g(np.concatenate([A, beta], axis=2))
    V_B = self.g(np.concatenate([B, alpha], axis=2))
    return V_A, V_B

16.5.1.3。聚合

有兩組比較向量vA,i (i=1,…,m） 和vB,j (j=1,…,n) 手頭，在最后一步中，我們將匯總此類信息以推斷邏輯關系。我們首先總結兩組：

(16.5.5)vA=∑i=1mvA,i,vB=∑j=1nvB,j.

接下來，我們將兩個匯總結果的串聯提供給函數h（一個MLP）得到邏輯關系的分類結果：

(16.5.6)y^=h([vA,vB]).

聚合步驟在以下類中定義Aggregate。

class Aggregate(nn.Module):
  def __init__(self, num_inputs, num_hiddens, num_outputs, **kwargs):
    super(Aggregate, self).__init__(**kwargs)
    self.h = mlp(num_inputs, num_hiddens, flatten=True)
    self.linear = nn.Linear(num_hiddens, num_outputs)

  def forward(self, V_A, V_B):
    # Sum up both sets of comparison vectors
    V_A = V_A.sum(dim=1)
    V_B = V_B.sum(dim=1)
    # Feed the concatenation of both summarization results into an MLP
    Y_hat = self.linear(self.h(torch.cat([V_A, V_B], dim=1)))
    return Y_hat

class Aggregate(nn.Block):
  def __init__(self, num_hiddens, num_outputs, **kwargs):
    super(Aggregate, self).__init__(**kwargs)
    self.h = mlp(num_hiddens=num_hiddens, flatten=True)
    self.h.add(nn.Dense(num_outputs))

  def forward(self, V_A, V_B):
    # Sum up both sets of comparison vectors
    V_A = V_A.sum(axis=1)
    V_B = V_B.sum(axis=1)
    # Feed the concatenation of both summarization results into an MLP
    Y_hat = self.h(np.concatenate([V_A, V_B], axis=1))
    return Y_hat

16.5.1.4。把它們放在一起

通過將參與、比較和聚合步驟放在一起，我們定義了可分解的注意力模型來聯合訓練這三個步驟。

class DecomposableAttention(nn.Module):
  def __init__(self, vocab, embed_size, num_hiddens, num_inputs_attend=100,
         num_inputs_compare=200, num_inputs_agg=400, **kwargs):
    super(DecomposableAttention, self).__init__(**kwargs)
    self.embedding = nn.Embedding(len(vocab), embed_size)
    self.attend = Attend(num_inputs_attend, num_hiddens)
    self.compare = Compare(num_inputs_compare, num_hiddens)
    # There are 3 possible outputs: entailment, contradiction, and neutral
    self.aggregate = Aggregate(num_inputs_agg, num_hiddens, num_outputs=3)

  def forward(self, X):
    premises, hypotheses = X
    A = self.embedding(premises)
    B = self.embedding(hypotheses)
    beta, alpha = self.attend(A, B)
    V_A, V_B = self.compare(A, B, beta, alpha)
    Y_hat = self.aggregate(V_A, V_B)
    return Y_hat

class DecomposableAttention(nn.Block):
  def __init__(self, vocab, embed_size, num_hiddens, **kwargs):
    super(DecomposableAttention, self).__init__(**kwargs)
    self.embedding = nn.Embedding(len(vocab), embed_size)
    self.attend = Attend(num_hiddens)
    self.compare = Compare(num_hiddens)
    # There are 3 possible outputs: entailment, contradiction, and neutral
    self.aggregate = Aggregate(num_hiddens, 3)

  def forward(self, X):
    premises, hypotheses = X
    A = self.embedding(premises)
    B = self.embedding(hypotheses)
    beta, alpha = self.attend(A, B)
    V_A, V_B = self.compare(A, B, beta, alpha)
    Y_hat = self.aggregate(V_A, V_B)
    return Y_hat

16.5.2。訓練和評估模型

現在我們將在 SNLI 數據集上訓練和評估定義的可分解注意力模型。我們從讀取數據集開始。

16.5.2.1。讀取數據集

我們使用16.4 節中定義的函數下載并讀取 SNLI 數據集 。批量大小和序列長度設置為256和50， 分別。

batch_size, num_steps = 256, 50
train_iter, test_iter, vocab = d2l.load_data_snli(batch_size, num_steps)

read 549367 examples
read 9824 examples

batch_size, num_steps = 256, 50
train_iter, test_iter, vocab = d2l.load_data_snli(batch_size, num_steps)

Downloading ../data/snli_1.0.zip from https://nlp.stanford.edu/projects/snli/snli_1.0.zip...
read 549367 examples
read 9824 examples

16.5.2.2。創建模型

我們使用預訓練的 100 維 GloVe 嵌入來表示輸入標記。因此，我們預先定義向量的維數 ai和bj在(16.5.1)中作為 100. 函數的輸出維度f在(16.5.1) 和g在(16.5.4)中設置為 200。然后我們創建一個模型實例，初始化其參數，并加載 GloVe 嵌入以初始化輸入標記的向量。

embed_size, num_hiddens, devices = 100, 200, d2l.try_all_gpus()
net = DecomposableAttention(vocab, embed_size, num_hiddens)
glove_embedding = d2l.TokenEmbedding('glove.6b.100d')
embeds = glove_embedding[vocab.idx_to_token]
net.embedding.weight.data.copy_(embeds);

embed_size, num_hiddens, devices = 100, 200, d2l.try_all_gpus()
net = DecomposableAttention(vocab, embed_size, num_hiddens)
net.initialize(init.Xavier(), ctx=devices)
glove_embedding = d2l.TokenEmbedding('glove.6b.100d')
embeds = glove_embedding[vocab.idx_to_token]
net.embedding.weight.set_data(embeds)

Downloading ../data/glove.6B.100d.zip from http://d2l-data.s3-accelerate.amazonaws.com/glove.6B.100d.zip...

16.5.2.3。訓練和評估模型

與第 13.5 節split_batch中 采用單一輸入（如文本序列（或圖像））的 函數相反，我們定義了一個函數來采用多個輸入，如小批量中的前提和假設。split_batch_multi_inputs

#@save
def split_batch_multi_inputs(X, y, devices):
  """Split multi-input `X` and `y` into multiple devices."""
  X = list(zip(*[gluon.utils.split_and_load(
    feature, devices, even_split=False) for feature in X]))
  return (X, gluon.utils.split_and_load(y, devices, even_split=False))

現在我們可以在 SNLI 數據集上訓練和評估模型。

lr, num_epochs = 0.001, 4
trainer = torch.optim.Adam(net.parameters(), lr=lr)
loss = nn.CrossEntropyLoss(reduction="none")
d2l.train_ch13(net, train_iter, test_iter, loss, trainer, num_epochs, devices)

loss 0.498, train acc 0.805, test acc 0.819
14389.2 examples/sec on [device(type='cuda', index=0), device(type='cuda', index=1)]

lr, num_epochs = 0.001, 4
trainer = gluon.Trainer(net.collect_params(), 'adam', {'learning_rate': lr})
loss = gluon.loss.SoftmaxCrossEntropyLoss()
d2l.train_ch13(net, train_iter, test_iter, loss, trainer, num_epochs, devices,
        split_batch_multi_inputs)

loss 0.521, train acc 0.793, test acc 0.821
4398.4 examples/sec on [gpu(0), gpu(1)]

16.5.2.4。使用模型

最后，定義預測函數輸出一對前提和假設之間的邏輯關系。

#@save
def predict_snli(net, vocab, premise, hypothesis):
  """Predict the logical relationship between the premise and hypothesis."""
  net.eval()
  premise = torch.tensor(vocab[premise], device=d2l.try_gpu())
  hypothesis = torch.tensor(vocab[hypothesis], device=d2l.try_gpu())
  label = torch.argmax(net([premise.reshape((1, -1)),
              hypothesis.reshape((1, -1))]), dim=1)
  return 'entailment' if label == 0 else 'contradiction' if label == 1 
      else 'neutral'

#@save
def predict_snli(net, vocab, premise, hypothesis):
  """Predict the logical relationship between the premise and hypothesis."""
  premise = np.array(vocab[premise], ctx=d2l.try_gpu())
  hypothesis = np.array(vocab[hypothesis], ctx=d2l.try_gpu())
  label = np.argmax(net([premise.reshape((1, -1)),
              hypothesis.reshape((1, -1))]), axis=1)
  return 'entailment' if label == 0 else 'contradiction' if label == 1 
      else 'neutral'

我們可以使用訓練好的模型來獲得樣本對句子的自然語言推理結果。

predict_snli(net, vocab, ['he', 'is', 'good', '.'], ['he', 'is', 'bad', '.'])

'contradiction'

predict_snli(net, vocab, ['he', 'is', 'good', '.'], ['he', 'is', 'bad', '.'])

'contradiction'

16.5.3。概括

可分解注意力模型由三個步驟組成，用于預測前提和假設之間的邏輯關系：參與、比較和聚合。

通過注意機制，我們可以將一個文本序列中的標記與另一個文本序列中的每個標記對齊，反之亦然。這種對齊是軟的，使用加權平均，理想情況下，大權重與要對齊的標記相關聯。

在計算注意力權重時，分解技巧導致比二次復雜度更理想的線性復雜度。

我們可以使用預訓練的詞向量作為下游自然語言處理任務（如自然語言推理）的輸入表示。

16.5.4。練習

使用其他超參數組合訓練模型。你能在測試集上獲得更好的準確性嗎？

用于自然語言推理的可分解注意力模型的主要缺點是什么？

假設我們想要獲得任何一對句子的語義相似度（例如，0 和 1 之間的連續值）。我們應該如何收集和標記數據集？你能設計一個帶有注意力機制的模型嗎？