一種常用的測量復雜正弦信號瞬時頻率的技術是計算信號瞬時 θ( n ) 相位的導數,如下面的圖 13–60所示。

圖 13–60 使用反正切函數的頻率解調器。
這是傳統的離散信號調頻解調方法,效果很好。解調器的瞬時輸出頻率為下面的 Eq13-111:
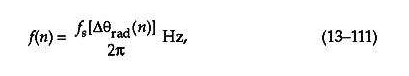
其中f s 是以赫茲為單位的采樣率。
計算瞬時相位 θ( n ) 需要反正切運算,如果沒有大量的計算資源,很難準確實現。這是用于計算等式Δθ( n )的方案。(13–111) 沒有中間 θ( n ) 相位計算(及其討厭的反正切函數)。我們推導出 ?θ( n ) 計算算法如下,初使用基于以下定義的連續時間變量:
i ( t ) = 同相信號,
q ( t ) = 正交相位信號,
θ( t ) = tan –1 [ q ( t )/ i ( t )] = 瞬時相位,
Δθ( t ) = 時間導數的 θ ( t )。(13-112)
首先,我們讓r ( t )= q ( t )/ i ( t ) 成為我們試圖計算其反正切導數的信號。微積分恒等式tan –1 [ r ( t )]的時間導數是
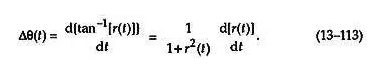
因為 d[ r ( t )]/dt = d[ q ( t )/ i ( t )]/dt,我們使用微積分恒等式對比率的導數來寫
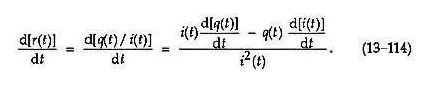
堵塞方程 (13–114) 的結果進入 Eq. (13–113),我們有
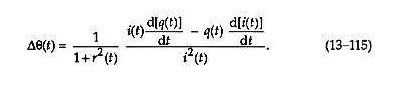
替換等式中的r ( t )。(13–115) 和q ( t )/ i ( t ) 產量
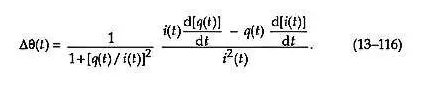
我們到了那里。接下來我們將方程式中個比率的分子和分母相乘。(13–116) 乘以i 2 ( t ),并將t替換為我們的離散時間變量索引n以得出我們的終結果
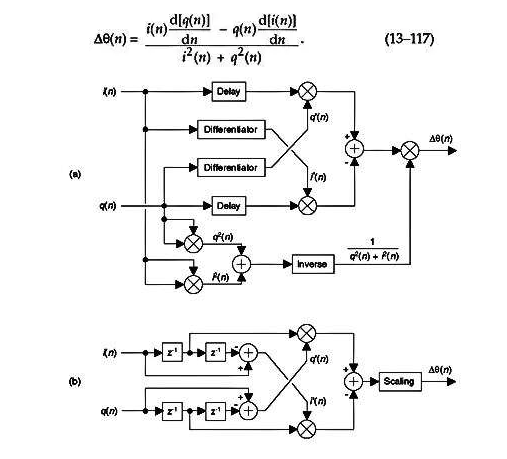
圖 13–61。 無反正切頻率解調器:(a)標準過程; (b) 簡化程序。
圖 13–61(a) 顯示了該算法的實現,其中i ( n ) 和q ( n ) 的導數分別為i ‘( n ) 和q ’( n )。Δφ( n ) 輸出序列用于等式。(13–111) 計算瞬時頻率。
微分器是抽頭數為奇數的抽頭延遲線 FIR 微分濾波器。當微分器是一個系數為 1,0,–1 的 FIR 濾波器時,參考文獻 [54] 了可接受的結果。
圖 13–61 中的延遲元件用于將i ( n ) 和q ( n ) 與微分器的輸出進行時間對齊,以便在使用K抽頭微分器時延遲為 ( K –1)/2 個樣本。 實際上,可以通過關閉微分濾波器的中心抽頭來獲得延遲。
如果i ( n )+ jq ( n ) 信號是純粹的 FM 和硬限制使得i 2 ( n )+ q 2 ( n ) = 常數,則方程式中的分母計算。(13–117) 不需要執行。在這種情況下,使用 1,0,–1 系數微分器,FM 解調器被簡化為圖 13–61(b) 中所示的解調器,其中縮放操作是乘以常數的倒數。
-
dsp
+關注
關注
552文章
7962瀏覽量
348256 -
解調器
+關注
關注
0文章
285瀏覽量
25793 -
變量
+關注
關注
0文章
613瀏覽量
28329
發布評論請先 登錄
相關推薦
車載FSK信號的2種解調算法及其DSP的應用實現
基于RLS算法的DPSK解調方法
基于DSP的寬頻逆變算法的研究與實現
基于DSP的軌道移頻信號解調實現
基于DSP的軌道移頻信號解調實現

基于DSP的軌道移頻信號解調實現方案解析
不同頻率頻段的電磁波的調制解調方法都不同嗎?
用TMS320C31 DSP實現聲碼器和短波調制解調器算法





 DSP技巧:頻率解調算法
DSP技巧:頻率解調算法










評論