本抖動簡介介紹了各種抖動類型的定義,包括隨機抖動類型:高斯、周期間、相鄰周期;和確定性抖動類型:占空比失真、脈沖寬度失真、脈沖偏斜和數據相關(模式)抖動。應用筆記還討論了各種抖動元件與系統誤碼率(BER)之間的關系。
什么是抖動?
SONET標準指出,“抖動被定義為數字信號的重要時刻從其理想位置在時間上的短期變化。重要時刻可能是(例如)最佳采樣時刻。光纖通道標準簡單地將抖動定義為“與事件理想時間的偏差”。
簡而言之,術語“抖動”描述了系統內的時序錯誤。在通信系統中,抖動的累積最終會導致數據錯誤。
對系統用戶最有價值的參數是這些數據錯誤的發生頻率,通常稱為誤碼率(BER)。稍后我們將更詳細地討論 BER。
首先,一些定義。基本抖動類型和定義如下表1所示。一些抖動類型有許多常用術語來描述相同的測量。其他術語描述了同一抖動類型的不同測量方法。如果使用多個術語來描述相同的抖動類型,則這些術語將一起列出。
| 抖動項 | 定義 | 附加信息 |
| 抖動 | 除了上述定義外,抖動還由兩種基本類型組成:隨機和確定性。 | |
| 隨機抖動 (RJ) | 無界抖動,可以用高斯概率分布來描述。隨機抖動的特征在于其標準偏差(rms)值。 | 主要來源是系統組件中的高斯(白色)電噪聲。電噪聲與信號的壓擺率相互作用,在開關點產生時序誤差。 |
| 隨機 | RJ測量方法。基于實際時鐘邊沿與其理想(預期)位置之間的時間差的概率分布。 | 盡管同一源的兩個測量值,但隨機和周期間抖動并不等效。周期間抖動具有頻率相關項,與隨機抖動測量相比,將加重高頻抖動源,同時抑制低頻源。隨機抖動測量與頻率無關。 |
|
循環到循環相鄰循環 |
RJ測量方法。基于一個時鐘周期和相鄰周期之間測量的周期差的概率分布。 | |
| 確定性抖動 (DJ) | 具有非高斯概率密度函數的抖動。總是有幅度和特定原因的限制。DJ的特點是其有限的,峰到峰的價值。 | 源通常與設備或傳輸介質行為的缺陷有關,但也可能是由于EMI、串擾、接地問題。 |
|
占空比失真 脈沖寬度失真 脈沖偏斜 |
DJ 組件。占空比值與理想(預期)值的偏差。在許多串行數據系統中,這相當于1位和0位之間的位時間偏差。也可以定義為低到高和高到低延遲時間之間的傳播延遲差異。 | 源通常是系統內上升沿和下降沿之間的時序差異。也可能是由單端系統中的接地偏移引起的。 |
|
數據相關抖動模式抖動 碼間干擾 |
DJ 組件。計時錯誤因使用的數據模式而異。數據相關和碼型抖動用于描述抖動在時域中的影響。碼間干擾更常應用于頻域測量,即頻譜分析儀上看到的信號峰值的擴展。 | 主要來源是組件和系統帶寬限制。高頻信號的建立時間比低頻信號短。這會導致不同頻率下轉換的起始條件發生變化,并產生取決于所應用數據模式的時序誤差。 |
|
正弦抖動 周期性抖動 |
DJ 組件。具有正弦(或周期性)形式且與數據模式相關(相關)的抖動。 | 源是來自與數據模式相關的信號的干擾。接地反彈和其他電源變化是常見原因,盡管通常遇到的正弦抖動水平非常低。 |
| 不相關的有界抖動 | DJ 組件。有界抖動 振幅和不相關(與數據模式)。 | 通常為正弦信號源,是來自系統內部或外部其他信號源的干擾。源包括 EMI、電容和電感耦合以及電源開關噪聲。 |
| 總抖動 (萬億焦耳) | 確定性和隨機抖動的總和(或卷積)。總抖動是獲得的峰峰值。 | TJ = DJ + n × RJ 其中 n = 對應于所需 BER 的標準差數。由于它很簡單,通常應用此求和,盡管這種方法高估了實際 BER,因為最大 RJ 誤差并不總是與最大 DJ 誤差一致。兩種抖動類型的概率(卷積)求和將產生更準確的解決方案,盡管應用它需要了解 DJ 調制波形。 |
| 映射抖動 | DJ 類型的系統級抖動分量。在映射過程中發生位填充時,由于數據從一個傳輸標準映射到另一個傳輸標準而導致的抖動。 | 去映射后,恢復的信號中會留下間隙。鎖相環(PLL)用于平滑產生的間隙,但仍存在一定量的抖動。 |
| 指針抖動 | DJ 類型的系統級抖動分量。由于將包含定義的指針活動序列的 SONET 信號應用于解復用器而導致抖動。 | |
| 徘徊抖動 | 系統級抖動分量 DJ類型。頻率小于 10Hz 的低頻定時誤差 (SONET)。 | 主要來源是系統溫度變化。 |
|
抖動傳輸 抖動增益 |
輸出信號上的抖動與輸入信號上的抖動之比。 | 用于量化數據重定時器件(再生器、PLL)的抖動累積性能。 |
| 抖動容限 | 接收器在不違反系統BER規范的情況下必須容忍的輸入抖動量。 | 可分為隨機抖動容限和確定性抖動容限。 |
| 單位間隔 (UI) | 相當于串行數據流中 1 位時間的時間段。 | 波特率的倒數。抖動規格通常以 UI 的倍數引用。 |
抖動如何導致數據錯誤?
通過在特定時刻對數據信號進行采樣,從串行數據流中提取信息。理想情況下,這些采樣時刻始終發生在數據位時間的中心,在兩個相鄰的邊沿轉換點之間等距。抖動的存在會改變相對于采樣點的邊沿位置。然后,當數據邊位于采樣時刻的錯誤一側時,將發生錯誤。
如表1所述,總抖動可以表示為確定性抖動和任何特定誤差概率值下隨機抖動的標準差數之和。隨機抖動在上面定義為抖動,可以用高斯概率分布來描述。高斯分布是圍繞平均值對稱的。一個標準差 (1σ) 定義為包含 68.26% 總體到均值一側的窗口。表2列出了σ的倍數,并列出了適用于每個倍數的總人口比例。
| 限制 | 限量內人口比例 |
| ±1秒 | 68.2689% |
| ±2秒 | 95.45% |
| ±3秒 | 99.73% |
| ±4秒 | 99.99367% |
| ±5秒 | 99.9999427% |
| ±6秒 | 100-1.973 × 10-7% |
| ±7秒 | 100-2.5596 × 10-10% |
| ±8秒 | 100-1.24419 × 10-13% |
| ±9秒 | 100-2.25718 × 10-17% |
| ±10秒 | 100-1.53398 x 10-21% |
確定性和隨機抖動求和的結果是另一種概率分布,其示例如圖1所示。該分布繪制概率與時序誤差幅度的關系圖,其特征在于具有表示確定性抖動成分的中心部分和作為(隨機抖動)高斯分布尾部的外部部分。所示的分布形狀稱為雙峰響應。
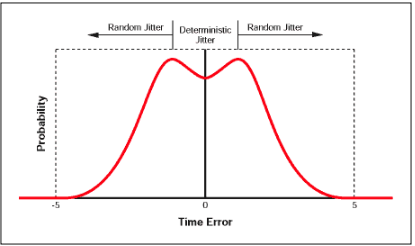
圖1.顯示確定性和隨機分量的概率直方圖。
將圖1所示的抖動概率分布添加到數據流中,可以有效地調制相對于采樣時刻的數據邊沿位置。如圖 2 所示,它顯示了疊加在數據轉移點上的概率直方圖的理想眼圖。與采樣時刻相關的數據錯誤的概率是第一個數據轉換到達得太晚或第二個數據轉換到達得太早的概率之和。該概率由圖 2 中采樣點曲線下方的陰影部分表示。
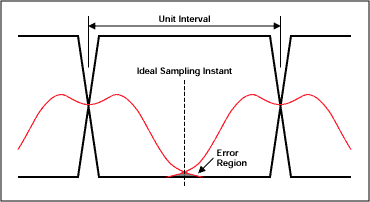
圖2.具有數據轉換時間概率直方圖的理想眼圖。
要找到發生數據錯誤的概率,必須將任一數據邊出錯的概率之和乘以實際發生轉換的概率。后者由平均轉換密度表示,并假設等于典型數據流的 50%。
舉個例子,考慮一個總確定性抖動為0.3UIp-p(包括所有非高斯時序誤差源)和0.05UI rms隨機抖動的數據流。最大允許抖動為1UIp-p;這是理想接收器在發生錯誤之前可以容忍的抖動量(請參閱下面的注釋)。使用公式 1 的表達式
DJ(pk) + n × RJ(rms) = TJ(pk)
代入TJ = 0.5UI(pk),DJ = 0.15UI(pk)和RJ = 0.05UI(rms),我們得到n = 7。這是將產生數據錯誤的隨機抖動的標準差 (σ) 數。對于高斯分布,1.28 × 10-10% 的樣本位于均值一側的 7σ 限制之外。總誤差率(BER)由公式2給出。
誤碼率 = (1.28 × 10?10% + 1.28 × 10?10%) × 50% = 1.28 × 10-10%
等式 2 的結果對應于 1.28 × 10 的 BER?12.
對應于±1σ至±10σ的隨機抖動限值的誤碼率見下表3。
| 限制 | 大約 |
| ±1秒 | 0.16 |
| ±2秒 | 2.28 × 10-2 |
| ±3秒 | 1.35 × 10-3 |
| ±4秒 | 0.32 × 10-4 |
| ±5秒 | 2.87 × 10-7 |
| ±6秒 | 0.98 × 10-9 |
| ±7秒 | 1.28 × 10-12 |
| ±8秒 | 0.62 × 10-15 |
| ±9秒 | 1.13 × 10-19 |
| ±10秒 | 0.77 × 10-23 |
注意:特定BER值下允許的最大抖動通常由系統規格或要求系統兼
審核編輯:郭婷
-
通信系統
+關注
關注
6文章
1176瀏覽量
53290 -
抖動
+關注
關注
1文章
69瀏覽量
18847
發布評論請先 登錄
相關推薦
如何測量扇出緩沖器中的附加抖動
超寬帶通信中定時抖動抑制算法的研究
時鐘抖動的基礎
通信系統中的抖動相關資料下載

扇出緩沖器中的附加抖動計算




 通信系統中抖動簡介
通信系統中抖動簡介
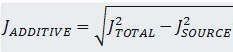











評論