層次分析法原理
層次分析法(Analytic Hierarchy Process,AHP)是一種多準則決策分析方法,可用于輔助決策者在多個指標或因素中進行排序或比較。該方法可以通過對多個因素進行兩兩比較獲得權(quán)重,從而建立一個層次結(jié)構(gòu),進而進行綜合評價和排名。
下面是一些詳解層次分析算法的步驟:
明確決策目標,確定需要評估的準則和子準則:首先明確決策目標,然后考慮需要評價的準則和子準則。這些準則和子準則應(yīng)該盡可能具體、完整,以便進行比較。
建立層次結(jié)構(gòu):將目標、準則和子準則構(gòu)成一個層次結(jié)構(gòu),其中目標位于最頂層,準則和子準則逐層展開,直到最底層。
對每個準則和子準則進行兩兩比較,得出權(quán)重:對于每個準則和子準則,根據(jù)它們對上一級準則或目標的相對重要性進行兩兩比較,生成判斷矩陣,并計算出每個準則和子準則相對于上一級準則或目標的權(quán)重。
計算一致性比率(CR):在計算權(quán)重時,需要考慮判斷矩陣的一致性。通過計算一致性指標和隨機一致性指標,可以得出一致性比率,并判斷結(jié)果是否可行。
綜合評價:根據(jù)各個準則和子準則的權(quán)重,可以得出每個方案的綜合評價。
層次分析法是一種較為常用的決策分析方法,應(yīng)用廣泛。但是,在實際應(yīng)用中需要注意判斷矩陣的構(gòu)造和一致性比率的計算,以確保評價結(jié)果的可靠性。
層次分析法數(shù)學模型
層次分析法 (Analytic Hierarchy Process, AHP) 包含的數(shù)學公式如下:
相對重要性矩陣
將兩兩比較得出的判斷矩陣記為 ,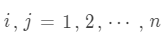 。其中, 表示因素 相對于因素 的相對重要度。
。其中, 表示因素 相對于因素 的相對重要度。
加權(quán)矩陣
將相對重要性矩陣 與準則/子準則的權(quán)重向量 相乘,得到加權(quán)矩陣 :
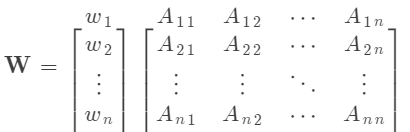
一致性指標
通過計算加權(quán)矩陣 的列和,得到一致性指標 :
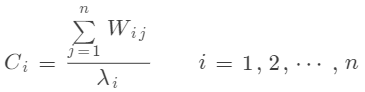
其中, 是與 相關(guān)的最大特征根。
隨機一致性指標
在 的范圍內(nèi),預(yù)先計算一組隨機一致性指標 ,然后計算隨機一致性比例 :
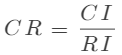
其中,CI 是一致性指標。
最終權(quán)重向量
當 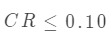 時,可將 當作最終權(quán)重向量。最終權(quán)重向量 可以通過歸一化加權(quán)矩陣得到:
時,可將 當作最終權(quán)重向量。最終權(quán)重向量 可以通過歸一化加權(quán)矩陣得到:
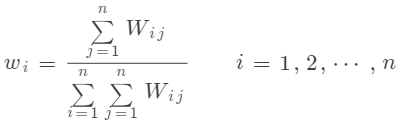
以上就是層次分析法中的主要數(shù)學公式。在具體應(yīng)用中,需要進行矩陣運算、特征根分解等數(shù)學操作。
MATLAB代碼實現(xiàn)
在 MATLAB 中實現(xiàn)層次分析法可以參考以下步驟:
構(gòu)造相對重要性矩陣
通過兩兩比較,構(gòu)造相對重要性矩陣 。在 MATLAB 中,可以使用 inputdlg() 函數(shù)獲取用戶輸入的相對權(quán)重值,再根據(jù)這些值構(gòu)造相對重要性矩陣。
例如,假設(shè)需要評估三個因素 A、B 和 C 的相對重要性,可以使用如下代碼創(chuàng)建相對重要性矩陣:
%獲取用戶輸入的相對權(quán)重值
prompt={'A相對于B的重要性:','A相對于C的重要性:','B相對于C的重要性:'};
name='輸入相對重要性';
numlines=1;
defaultans={'','',''};
answer=inputdlg(prompt,name,numlines,defaultans);
%構(gòu)造相對重要性矩陣
A=[1str2double(answer{1})str2double(answer{2});
1/str2double(answer{1})1str2double(answer{3});
1/str2double(answer{2})1/str2double(answer{3})1];
計算權(quán)重向量
計算準則/子準則的權(quán)重向量 ,可以用 eig() 函數(shù)計算相對重要性矩陣 的特征向量和特征值,再將特征向量進行歸一化。
例如,使用如下代碼計算權(quán)重向量:
%計算特征向量和特征值 [eigvec,eigval]=eig(A); %獲取最大特征值的索引 [~,max_eigval_index]=max(diag(eigval)); %獲取對應(yīng)的特征向量,并進行歸一化 w=eigvec(:,max_eigval_index); w=w/sum(w);
檢驗一致性
計算一致性指標 和隨機一致性比例 ,判斷評價結(jié)果的可靠性。通常,當 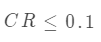 時,可以認為評價結(jié)果可靠。
時,可以認為評價結(jié)果可靠。
例如,使用如下代碼進行一致性檢驗:
%計算一致性指標 CI=(max(diag(eigval))-3)/(n-1); %預(yù)先計算隨機一致性比例 RI=[000.580.91.121.241.321.411.451.51]; %計算隨機一致性比例 CR=CI/RI(n);
輸出結(jié)果
輸出準則/子準則的權(quán)重向量和一致性檢驗結(jié)果。例如,使用如下代碼輸出結(jié)果:
%輸出權(quán)重向量 fori=1:n fprintf('%s的權(quán)重:%.4f ',criteria{i},w(i)); end %輸出一致性檢驗結(jié)果 fprintf('一致性指標CI=%.4f,隨機一致性比例CR=%.4f ',CI,CR); ifCR<=?0.1 ????fprintf('一致性檢驗通過,評價結(jié)果可靠。 '); else ????fprintf('一致性檢驗未通過,評價結(jié)果不可靠。 '); end
以上就是在 MATLAB 中實現(xiàn)層次分析法的主要步驟。需要注意的是,層次分析法的實現(xiàn)過程中需要進行矩陣運算和特征值計算等較為復雜的操作,建議使用函數(shù)封裝實現(xiàn)。
責任編輯:彭菁
-
matlab
+關(guān)注
關(guān)注
182文章
2963瀏覽量
230149 -
函數(shù)
+關(guān)注
關(guān)注
3文章
4304瀏覽量
62427
原文標題:層次分析法(原理+數(shù)學模型+代碼實現(xiàn))
文章出處:【微信號:嵌入式職場,微信公眾號:嵌入式職場】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
基于灰色層次分析法的戰(zhàn)場電磁環(huán)境效應(yīng)評估
層次分析法是什么
層次分析法及其在電力系統(tǒng)中的應(yīng)用
層次分析法的改進及應(yīng)用
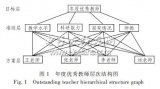
算法大全_層次分析法
基于層次分析法的電網(wǎng)應(yīng)急演練管理系統(tǒng)研究與實現(xiàn)
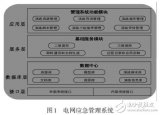
基于模糊層次分析法的安全態(tài)勢評估中
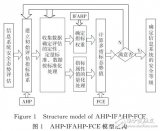




 在 MATLAB 中實現(xiàn)層次分析法的主要步驟
在 MATLAB 中實現(xiàn)層次分析法的主要步驟










評論