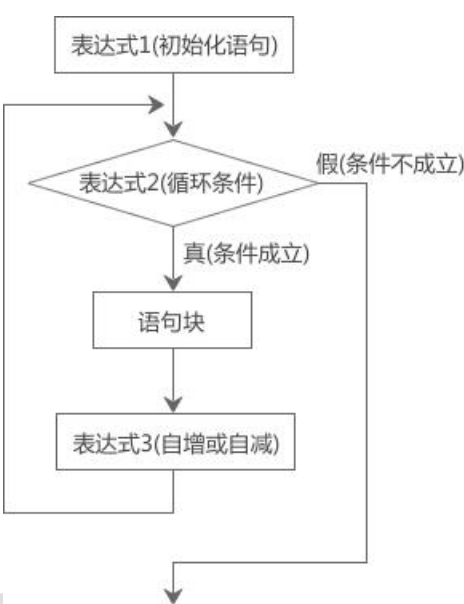
1.for循環
for(表達式1;表達式2;表達式3)
{
語句塊
}
表達式1:表示的是初始化條件;
表達式2:循環條件
表達式3:自增或自減
for循環中三個表達式都可以省略,但分號必須保留。
- 示例:計算1+2+3+...+100
#include
/*
計算1+2+3+...+100
*/
int main()
{
int i;
int sum=0;
for(i=1;i<=100;i++)
{
printf("i=%dn",i);
sum+=i;//sum=sum+i;
}
printf("sum=%dn",sum);
}
1.1 for循環嵌套
#include
int main()
{
int i,j;
int cnt=0;
for(i=0;i
注意:break只能跳出一層循環
2.while循環
while(表達式)
{
語句塊
}
- 示例:2+4+6+8...+100
#include
/*
示例:2+4+6+8...+100
*/
int main()
{
int i=2;
int sum=0;
while(i<=100)
{
sum+=i;
i+=2;
}
printf("sum=%dn",sum);
}
3.do..while循環
do
{
語句塊
}while(表達式);
while和do...while區別:while循環條件為真才能執行里面的語句塊,do...while先執行一次語句塊,再判斷條件。
4.循環控制語句
| 控制語句 | 描述 |
| break語句 | 終止循環或switch語句,程序將執行緊接著循環或switch的下一條語句 |
| continue語句 | 立刻停止本輪循環,重新開始下輪循環 |
| goto語句 | 將控制跳轉到被標記的語句。不太建議程序中使用goto語句 |
4.1 break語句
C語言中break語句有以下兩種用法:
①用于循環語句中,當break語句出現在一個循環內時,循環會立即終止,且程序流將繼續執行緊接著循環的下一條語句。
②用于switch結構中,它可用于終止switch語句中的一個case。
如果使用的是嵌套循環(即一個循環內嵌套另一個循環), break語句會停止執行其所在的那層循環,然后開始執行該塊之后的下一行代碼。
4.2 continue語句
C語言中的continue語句有點像 break 語句。但它不是強迫終止, continue會結束當前循環中的代碼,強迫開始下一次循環。
對于for循環,continue語句執行后自增語句仍然會執行。
對于while和do...while循環,continue 語句會重新執行條件判斷語句。
4.3 goto語句
C語言中的goto語句允許把控制無條件轉移到同一函數內的被標記的語句。
注意:在任何編程語言中,都不建議使用goto語句。一是因為它使得程序的控制流難以跟蹤,使程序難以理解和難以修改。任何使用goto語句的程序可以改寫成不需要使用goto語句的寫法。二是goto語句容易破壞原本的代碼結構。
C語言中goto語句的語法:
Label:
printf("goto語句使用!n");
.....
語句塊;
...
goto Label:
在這里,label可以是任何除C關鍵字以外的純文本,它可以設置在C程序中goto語句的前面或者后面。
5.練習
1.求100以內自然數中偶數之和。
2.輸出200~400以內能被3整除且個位數字為6的整數。
3.計算:1*2*3+3*4*5+。。。。 +99*100*101 的值。
4.輸出所有水仙花數。(水仙花數:一個三位數,它的每個位上的數字的3次冪只和等于他本身)
5.排列組合問題:一個口袋中放有12個球,已知其中3個是紅色的,3個是白色的,6個是黑色的,現在從中任取8個,問共有多少種可能的顏色搭配。
6.判斷2~100之間所有素數。(只能被本身整除的數,比如:3 、7、13。
7.輸出2~1000之間的可逆素數。
8.打印正三角形和倒三角形。

9.輸出9*9乘法表。
10.韓信點兵:相傳韓信才智過人,從不直接清點自己軍隊的人數,只要讓士兵先后以三人一排、五人一排、七人一排地變換隊形,而他每次只掠一眼隊伍的排尾就知道總人 數了。請輸入3個非負整數a,b,c ,表示每種隊形排尾的人數(a<3,b<5,c<7),輸出總人數的最小值(或報告無解)。已知總人數不小于10,不超過100 。
11.有一個4位數,它的9倍數恰好是其反序數,求該數。(反序數就是將其倒過來形參的整數,例1234的反序數就是4321。)
12.求一個三位數,該三位數等于其每個位數字的階乘之和。
13.輸出1000以內所有的完全數。(完全數:一個數恰好等于它的因子之和。如6的因子為1 2 3,而1+2+3=6)
14.輸出具有abcd=(ab+cd)2性質的四位數。
15.將100元換成1元、5元、10元有多少種換法?
16.百元買白雞問題:100塊錢買100只雞,公雞5塊1只、母雞3塊1只,小雞3只1塊,輸出所有的買法。
17.有一個數列:1、1、2、3 、5 、8...
通過輸入下標,輸出對應的值,下標從1開始。例如輸入3,輸出2;輸入5,輸出5;
18.愛因斯坦出了一道這樣的數學題:有一條長階梯,若每步跨⒉階,則最后剩1階,若每步跨3階﹐則最后剩⒉階,若每步跨5階,則最后剩4階,若每步跨6階則最后剩5階。只有每次跨7階,最后才正好一階不剩。請問,這條階梯共有多少階?
19.一輛卡車違反交通規則,撞人后逃跑。現場有三人目擊事件,但都沒有記住車號,只記下車號的一些特征(假設僅為數字)。
甲說:牌照的前兩位數字是相同的;
乙說:牌照的后兩位數字是相同的,但與前兩位不同;
丙是位數學家,他說:四位的車號剛好是一個整數的平方。請根據以上線索求出車號。
20.如果一個數恰好等于它的因子之和,則稱該數為“完全數”。如:6的因子是1、2、3,而6=1+2+3,則6是個“完全數”。試求出1000以內的全部“完全數”。
21.誰在說謊問題:張三說李四在說謊,李四說王五在說謊,王五說張三和李四都在說謊。現在問:這三人中到底誰說的是真話,誰說的是假話?
審核編輯:湯梓紅
-
C語言
+關注
關注
180文章
7575瀏覽量
133986 -
關鍵字
+關注
關注
0文章
37瀏覽量
6880 -
循環語句
+關注
關注
0文章
8瀏覽量
4844
發布評論請先 登錄
相關推薦




 C語言基礎知識(5)--循環語句
C語言基礎知識(5)--循環語句












評論