MATLAB?是一個強有力的工具,可用來快速分析從模數轉換器(ADC)輸出所捕獲的數據。本應用筆記演示了如何使用MATLAB來突破邏輯分析儀存儲深度的局限。描述并比較了三種數碼拼接方式(基本,超前和反轉)。并給出了三種方法所得的結果。
介紹
要評估一個高速模數轉換器(ADC)的性能,就需要捕獲其數字輸出碼,然后進行分析。邏輯分析儀的存儲深度常常成為一個重要局限,妨礙系統捕獲足夠的數據點,以生成高分辨率FFT,或者精確的INL/DNL圖。解決該問題的一個簡單辦法是使用某種數學工具,例如MATLAB ( 圖1 ),將多組數據連接起來。連接數據的一個缺點是,通常會在兩組數據之間的連接點出現很大的不連續性。盡管不連續性對INL/DNL圖的影響極小,但對高分辨率FFT而言,幾乎是毀滅性的( 圖2 )。
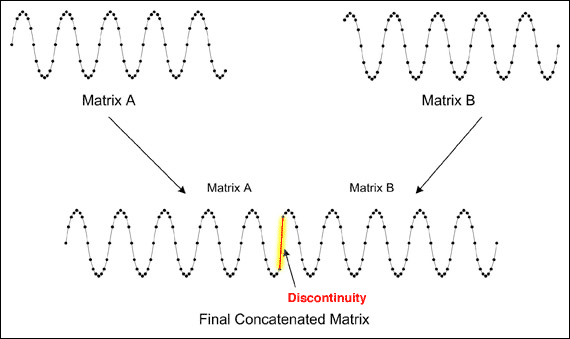
圖1. 連接后的數據在兩組數據之間出現不連續。
![圖2. a) 捕獲單組16384點數據并分析;b) 捕獲兩組8192點數據,連接,然后分析“拼接”技術。]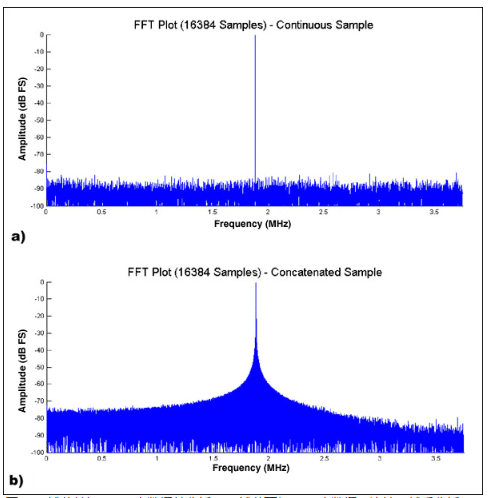
圖2. a) 捕獲單組16384點數據并分析;b) 捕獲兩組8192點數據,連接,然后分析“拼接”技術。
有一種辦法可以消除不連續性,就是在各組數據中尋找相同的點簇(一般為3到4個點),然后在這些點將兩組數據“拼接”在一起( 圖3 )。最簡單的“拼接”方法是,記錄下第一組數據中的最后四個點,然后在第二組數據里尋找相同的點簇。相同點簇出現在第二組數據中的位置稱為“拼接點”。第二組數據中在拼接點之前的所有數據均被舍棄;第二組數據中的剩余部分與第一組數據合并。這種技術即所謂的基本數碼拼接,實現起來非常簡單,可以在MATLAB中非常快地運行。
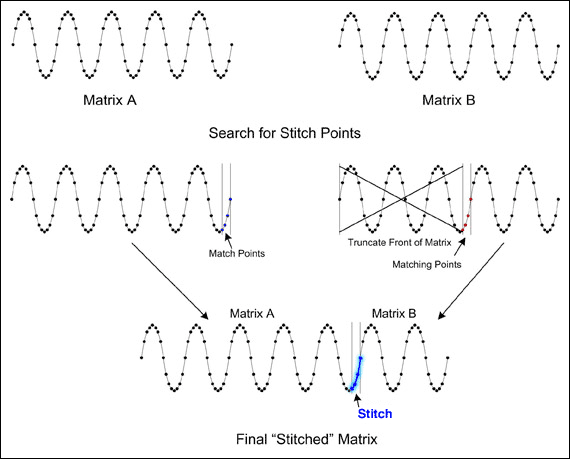
圖3. 基本數碼拼接后得到的最終“拼接”數組。
采用基本拼接方法拼接數據時,有時必須丟掉第二組數據中的近一半,才能找到與第一組數據最后四個點相匹配的一簇點。作為另一種選擇,丟掉第一組數據尾部的幾個點,常常有助于找到更靠近第二組數據起點的拼接點( 圖4 )。然而,通過丟掉第一組數據尾部、第二組數據頭部的部分采樣點來尋找匹配點的方法實現起來比較困難。這種處理被稱為超前數碼拼接。理想拼接點應該能夠保留盡可能多的數據點,尋找這樣的拼接點需要認真的考慮和一定的編程技巧。正確地實現之后,超前拼接技術通常能夠得到兩組小數組所含數據點總數的至少90%。
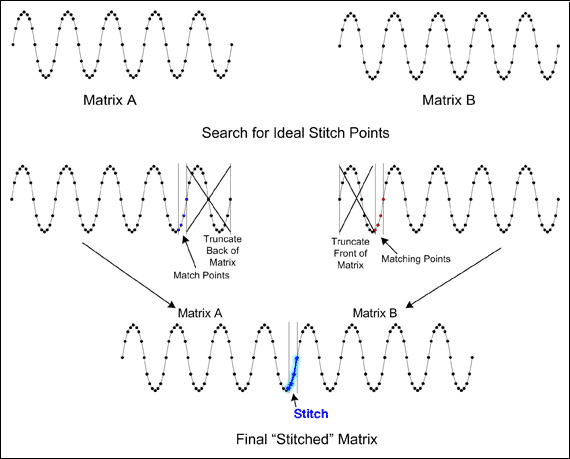
圖4. 采用超前拼接技術尋找理想拼接點,最終得到“拼接”后的數組。
將第二組數據(數組B)拼接到第一組數據(數組A)之前被稱為反轉拼接,這種方式有可能得到更大的拼接數組( 圖5 )。但是,這種技術會使處理時間翻倍,因為必須在A領先于B和B領先于A兩種情況下尋找拼接點。此外,當與其他拼接技術一起使用時,反轉拼接方式所帶來的好處通常很少。因此,對于較慢的PC,反轉拼接技術大幅度增加的處理時間開銷較之它所帶來的好處而言并不太值。表1詳細比較了這三種代碼拼接方法。
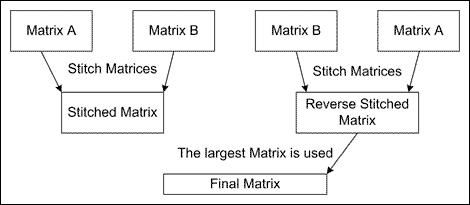
圖5. 反轉拼接的處理時間加倍,但常常收效甚微。
表1. 三種拼接技術對比 *
| Stitch Technique | Size of Final Data Set | Description |
|---|---|---|
| Data Set Numbers | # of codes(averaged) | % of two data sets(averaged) |
| 1 + 2 | 3 + 4 | 1 + 4 |
| Concatenate? | N/A | 16384 |
| Basic | 11060 | 8192? |
| Reverse | 11060 | 8192? |
| Advanced | 13790 | 16046 |
| Advanced+Reverse | 15427 | 16176 |
*采用上述拼接技術對兩組8K (8192個)數據進行拼接。為確保準確性,采用四組8192點數據(分別編號為1至4)重復本測試。每組測試所合成的數據取平均后列于測試數據的右側。
? 直接連接總能得到100%的數據。
? 無法拼接數據。### MATLAB函數說明
本文后附的MATLAB代碼(附錄A和B中的StitchMatrices和FindStitchPoint)將上述論點結合到一個易于使用的函數中。這些函數可接受兩組數據(MATLAB中的單列矩陣)和幾個輸入變量(用來選擇超前/反轉拼接功能)。FindStitchPoint例程用來確定拼接點在數組A和B中的偏移量。StitchMatrices例程則根據FindStitchPoint例程給出的偏移量對兩組數據A和B進行舍棄和組合。同時,最終數據的拼接點被記錄在PrevStitchBins數組中,以便于后續處理。當拼接多組數據時,PrevStitchBins可保存老的拼接點。
結論
拼接兩組數據可以得到一組理想的結果。圖6給出了三組8192點數據使用上述拼接技術拼接起來(使用5個拼接點)后的FFT圖。所得的FFT幾乎與前面圖2a所示,基于16384個連續點所得結果相同。
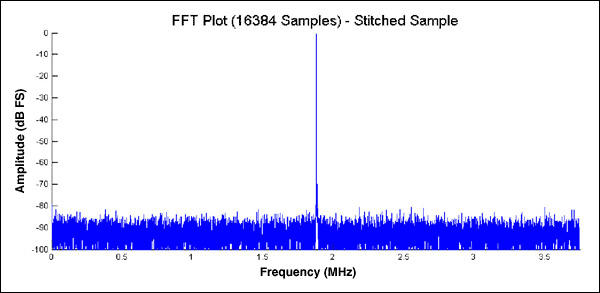
圖6. 數碼拼接后得到精確的FFT圖。
審核編輯:郭婷
-
matlab
+關注
關注
182文章
2963瀏覽量
230154 -
adc
+關注
關注
98文章
6434瀏覽量
544087
發布評論請先 登錄
相關推薦
邏輯分析儀是什么
RAM內存不足錯誤
邏輯分析儀內存不足?“拼”出解決之道
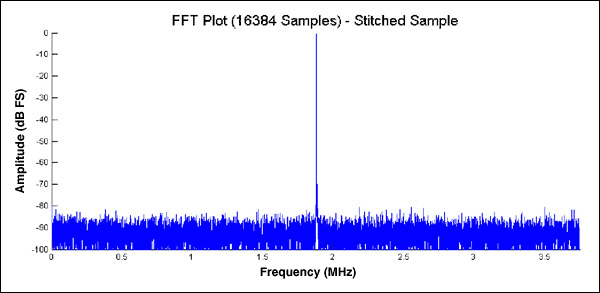




 邏輯分析儀內存不足? “拼”出解決之道!
邏輯分析儀內存不足? “拼”出解決之道!










評論