在聽過很多關于數字信號處理(DSP)技術的知識之后,您可能想了解DSP可以做什么,研究為什么DSP在許多類型的操作中比模擬電路更受歡迎,并了解如何學到足夠的知識來設計自己的DSP系統。本文是系列文章的第一篇,是朝著尋找問題的答案邁出重要的第一步的機會。本系列從尋求更多工具處理模擬信號的模擬系統設計人員的角度介紹DSP主題。閱讀本系列的設計人員可以了解DSP處理模擬信號的可能性,以及在哪里可以找到其他信息和幫助來源。
什么是DSP?簡而言之,DSP是處理器或微型計算機,其硬件、軟件和指令集針對高速數字處理應用進行了優化,這對于實時處理表示模擬信號的數字數據至關重要。DSP的作用很簡單。例如,當充當數字濾波器時,DSP根據信號樣本接收數字值,計算對這些值進行操作的濾波器功能的結果,并提供代表濾波器輸出的數字值;它還可以根據這些值的屬性提供系統控制信號。DSP的高速算術和邏輯硬件經過編程,可快速執行模擬濾波器變換的算法。
提供這種能力的設計元素算術運算符、存儲器處理、指令集、并行性、數據尋址的組合構成了 DSP 與其他類型的處理器之間的關鍵區別。了解實時信號和DSP計算速度之間的關系,為這種組合的特殊性提供了一些背景知識。實時信號作為一系列來自模數轉換器(ADC)的單個樣本進入DSP。為了實時進行濾波,DSP必須在下一個樣本到達之前完成處理每個樣本所需的所有計算和操作(通常更新涉及許多先前樣本的過程)。為了對具有大量頻率內容的真實信號執行高階濾波,需要真正快速的處理器。
為什么要使用 DSP?
為了了解DSP的計算類型,并了解模擬電路與DSP系統的比較情況,可以根據濾波器功能比較這兩個系統。熟悉的模擬濾波器使用電阻器、電容器、電感器、放大器。它可以便宜且易于組裝,但難以校準、修改和維護隨過濾器順序呈指數級增長的難度。出于多種目的,使用DSP可以更輕松地設計、修改和依賴濾波器,因為DSP上的濾波器功能基于軟件、靈活且可重復。此外,要創建具有高階響應的靈活可調濾波器,只需修改軟件,與純模擬電路不同,無需額外的硬件。理想的帶通濾波器具有圖1所示的頻率響應,具有以下特性:
通帶內的響應完全平坦,相移為零
阻帶中的無限衰減。
有用的補充包括:
通帶調諧和寬度控制
阻帶滾降控制。
如圖1所示,使用二階濾波器的模擬方法需要相當多的交錯高Q值部分;調整和調整它的難度可想而知。
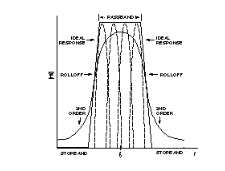
圖1.理想的帶通濾波器和二階近似。
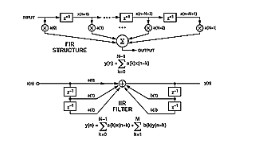
使用DSP軟件,濾波器設計有兩種基本方法:有限脈沖響應(FIR)和無限脈沖響應(IIR)。FIR濾波器對脈沖的時間響應是當前和有限數量的先前輸入樣本的直接加權和。在沒有反饋的情況下,當樣品到達“線的末端”時,它對給定樣品的響應結束(圖2)。FIR濾波器的頻率響應沒有極點,只有零點。相比之下,IIR 濾波器被稱為無限,因為它是一個遞歸函數:它的輸出是輸入和輸出的加權和。由于它是遞歸的,因此它的響應可以無限期地繼續。IIR濾波器頻率響應具有極點和零點。
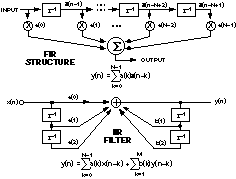
圖2.濾波器方程和延遲線表示。
xs 是輸入樣本,ys 是輸出樣本,as 是輸入樣本權重,bs 是輸出樣本權重。n 是當前采樣時間,M 和 N 是編程的采樣數(濾波器的順序)。請注意,為這兩種類型指示的算術運算只是總和和乘積,可能數量很大。事實上,乘加法是許多DSP算法的情況,這些算法表示非常精密和復雜的數學運算。
近似理想濾波器包括應用具有適當系數和足夠高階數或抽頭數的傳遞函數(將輸入樣本序列視為抽頭延遲塊)。圖3顯示了90抽頭FIR濾波器與各種階次銳截止切比雪夫濾波器的響應。90抽頭示例表明濾波器可以接近理想濾波器的程度。在DSP系統中,對圖90所示的3抽頭FIR濾波器進行編程并非易事。相比之下,使用純模擬電路嘗試這種近似水平并不具有成本效益。支持使用DSP近似理想濾波器的另一個關鍵點是長期穩定性。使用FIR(或具有足夠分辨率以避免截斷誤差累積的IIR),可編程DSP可以一次又一次地實現相同的響應。高階純模擬濾波器響應隨時間推移不太穩定。
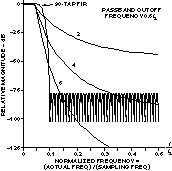
圖3.90抽頭FIR濾波器響應與尖銳截止切比雪夫濾波器的響應相比。
數學變換理論和實踐是創建DSP應用和理解其局限性的核心要求。本系列文章通過幾個信號分析和處理示例來介紹DSP概念。該系列還提供了進一步研究的文本參考,并確定了簡化信號處理軟件開發的軟件工具。
對真實信號進行采樣
現實世界的現象模擬了聲音、光、熱、電、磁等物理過程不斷變化的能級。傳感器將這些電平轉換為可管理的電壓和電流信號,ADC對這些信號進行采樣并將其轉換為數字信號進行處理。ADC的轉換速率或采樣頻率在實際信號的數字處理中至關重要。
該采樣率由為給定應用充分處理信號所需的信號信息量決定。為了使ADC提供足夠的樣本來準確描述實際信號,采樣速率必須至少是模擬信號最高頻率分量的兩倍。例如,為了準確描述包含高達20 kHz頻率的音頻信號,ADC必須以至少40 kHz的頻率對信號進行采樣。由于到達信號很容易包含高于20 kHz的元件頻率(包括噪聲),因此在采樣之前,必須通過ADC之前的低通濾波器饋送信號來消除它們。該濾波器稱為抗混疊濾波器,旨在消除20 kHz以上可能破壞轉換信號的頻率。
但是,抗混疊濾波器的頻率滾降有限,因此必須為濾波器的過渡帶提供額外的帶寬。例如,輸入信號帶寬為 20 kHz 時,可能允許 2 到 4 kHz 的額外帶寬。
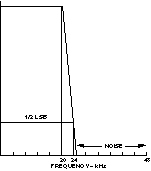
圖4.抗混疊濾波器理想響應。
圖4顯示了抑制頻率高于48 kHz采樣速率一半的任何信號所需的濾波器。抑制意味著衰減到ADC分辨率的1/2最低有效位(LSB)以下。在沒有高度復雜的模擬濾波器的情況下實現這種抑制水平的一種方法是使用過采樣轉換器,例如Σ-Δ型ADC。它通常以兆赫茲速率獲得低分辨率(例如,1位)樣本,比最高頻率分量的兩倍快得多,大大減輕了對轉換器前面的模擬濾波器的要求。內部數字濾波器(工作中的DSP!)恢復所需的分辨率和頻率響應。對于許多應用,過采樣轉換器可減少系統設計工作量和成本。
處理真實信號
ADC采樣速率取決于被采樣模擬信號的帶寬。此采樣率設定了可供處理的樣本的速度。一旦系統帶寬要求確定了A/D轉換器采樣速率,設計人員就可以開始探索DSP處理器的速度要求。
所需采樣率下的處理速度受算法復雜性的影響。通常,DSP需要在接收第二個樣本之前完成與第一個樣本相關的所有操作。采樣間隔時間是DSP執行所有處理任務的時間預算。對于音頻示例,48 kHz 采樣率對應于 20.833 μs 采樣間隔。圖5顯示了模擬信號和數字采樣速率。
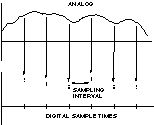
圖5.采樣訓練和處理時間。
接下來考慮DSP的速度與算法(包含變換或其他數字運算集的軟件)的復雜性之間的關系。復雜的算法需要更多的處理任務。由于樣品之間的時間是固定的,因此復雜性越高,處理速度越快。例如,假設該算法要求在樣本之間執行 50 個處理操作。使用前面示例的 48 kHz 采樣率(20.833 μs 采樣間隔),可以計算所需的最低 DSP 處理器速度,以每秒百萬次操作 (MOPS) 為單位,如下所示:
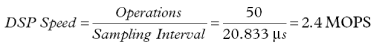
因此,如果樣本之間的所有時間都可用于實現算法的操作,則需要性能級別為 2.4 MOPS 的處理器。請注意,基于每秒操作數 (MOPS) 和每秒指令數 (MIPS) 的 DSP 的兩個常見額定值并不相同。具有 10-MIPS 額定值的處理器,每條指令可以執行 8 個操作,其性能與具有 40 MIPS 額定值的更快處理器的性能基本相同,每個指令只能執行 2 個操作。
對各種真實信號進行采樣
有兩種基本方法可以獲取數據,一次一個樣本或一次一個幀(連續處理與批處理)。基于樣本的系統,如數字濾波器,一次采集一個樣本的數據。如圖6所示,在時鐘的每個時鐘周期,一個樣本進入系統,并輸出一個處理后的樣本。輸出波形不斷發展。
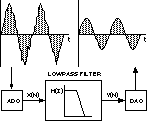
圖6.在數字濾波器中連續處理樣品的示例。
基于幀的系統,如頻譜分析儀,用于確定時變波形的頻率分量,獲取幀(或樣本塊)。處理發生在整個數據幀上,并生成轉換后的數據幀,如圖 7 所示。
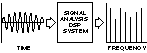
圖7.數據塊的批處理示例。
對于 48 kHz 的音頻采樣率,處理 1024 個樣本幀的處理器的幀采集間隔為 21.33 毫秒(即 1024 x 20.833 μs = 21.33 毫秒)。在這里,DSP有21.33毫秒的時間來完成該數據幀所需的所有處理任務。如果系統實時處理信號,則不得丟失任何數據;因此,當DSP處理第一幀時,它也必須獲取第二幀。數據采集是DSP特殊架構特性發揮作用的一個領域:處理器靈活的數據尋址功能與其直接存儲器訪問(DMA)通道相結合,有助于實現無縫數據采集。
響應真實世界的信號
不能假設樣本之間的所有時間都可用于執行處理指令。實際上,必須為處理器準備時間以響應外部設備,從而控制數據的進出。通常,外部設備(如ADC)使用中斷向處理器發出信號。DSP對該中斷的響應時間或中斷延遲直接影響實際信號處理的剩余時間。
中斷延遲(響應延遲)取決于幾個因素;最主要的是DSP架構的指令流水線。指令流水線由接收中斷和程序執行恢復之間發生的指令周期數組成。DSP 中的流水線級別越高,中斷延遲就越長。例如,如果處理器的周期時間為 20 ns,并且需要 10 個周期來響應中斷,則在執行任何信號處理指令之前需要 200 ns。
當一次采集一個樣本的數據時,如果DSP在下一個樣本到達之前完成對每個樣本的處理,則200 ns開銷不會受到傷害。然而,當在一次處理一幀時逐個樣本地采集數據時,中斷的系統會浪費處理器指令周期。例如,運行基于幀的算法(如FFT)的中斷響應時間為200 ns的系統,幀大小為1024個樣本,將需要204.8 μs的開銷。這相當于浪費了超過10,000個指令周期,以延遲DSP可以執行信號處理的生產時間。在具有DMA和雙存儲器訪問等架構特性的DSP中,這種浪費很容易避免;它們使DSP在不中斷處理器的情況下接收和存儲數據。
開發數字數字信號處理器系統
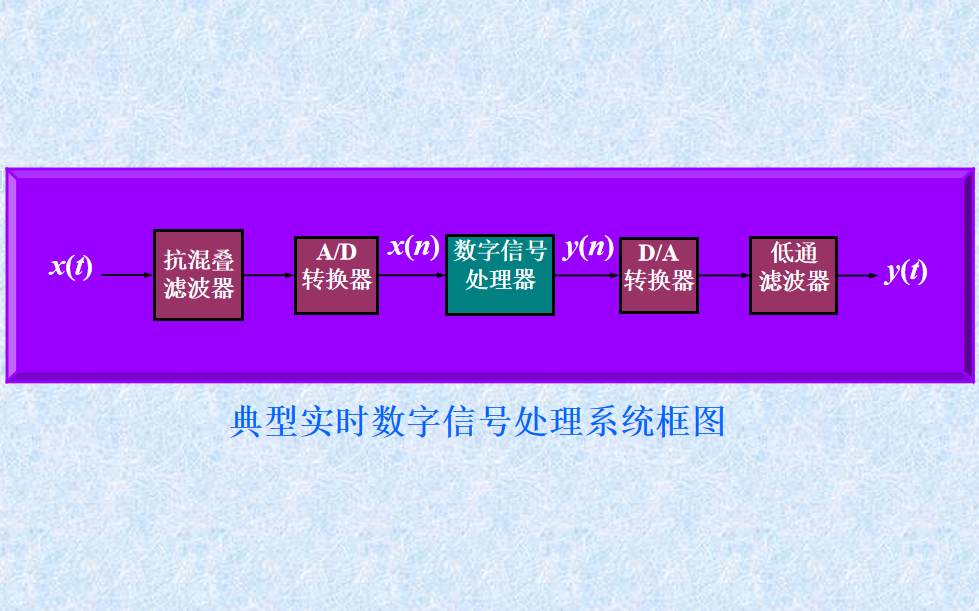
在討論了處理器、ADC、抗混疊濾波器的作用以及這些組件之間的時序關系之后,現在是時候了解一個完整的DSP系統了。圖8顯示了可用于數據采集和控制的典型DSP系統的構建模塊。
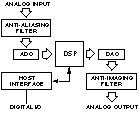
圖8.將 DSP 系統的元素組合在一起。
請注意,組成DSP系統的組件很少,因為系統的大部分功能都來自可編程DSP。轉換器將數據漏入和漏出DSP;ADC時序由精密采樣時鐘控制。為了簡化系統設計,目前可用的許多轉換器器件都結合了以下部分或全部功能:A/D轉換器、D/A轉換器、采樣時鐘以及用于抗混疊和抗成像的濾波器。這些類型的I/O組件中的時鐘振蕩器由外部晶體單獨控制。以下是有關此類DSP系統中數據流的一些要點:
模擬輸入:模擬信號由抗混疊濾波器適當限制頻帶,并施加到ADC的輸入端。在選定的采樣時間,轉換器中斷DSP處理器并使數字采樣可用。ADC和DSP之間的串行和并行接口之間的選擇取決于數據量、設計復雜性權衡、空間、功耗和價格。
數字信號處理:傳入的數據由DSP的算法軟件處理。當處理器完成所需的計算時,它將結果發送到DAC。由于信號處理是可編程的,因此在處理數據和通過增量編程調整提高系統性能方面具有相當大的靈活性。
模擬輸出:DAC在下一個采樣時鐘將DSP的輸出轉換為所需的模擬輸出。轉換器的輸出由低通抗成像濾波器(也稱為重建濾波器)平滑,以產生重建的模擬信號。
主機接口:可選的主機接口允許DSP與外部系統通信,發送和接收數據和控制信息。
本文旨在概述主要的DSP設計概念,并解釋為什么DSP更適合某些應用的模擬電路的一些原因。本文介紹的問題包括:
數字信號處理器概述
實時數字數字信號處理器操作
真實信號
采樣率和抗鋸齒濾波
DSP 算法時間預算
樣本驅動數據采集與幀驅動數據采集
由于這些問題涉及許多有價值的細節級別,我們無法在這篇簡短的文章中公正地對待,因此您應該考慮閱讀Richard Higgins的文本,VLSI中的數字信號處理(請參閱下面的參考文獻)。本文提供了DSP理論、實現問題和實踐簡化(發布時可用的設備)的完整概述,以及練習和示例。下面的參考部分還包含進一步放大本文問題的其他來源。為準備本系列的下一篇文章,您可能需要免費獲取ADSP-2100系列用戶手冊*和ADSP-2106x SHARC用戶手冊。 這些文本提供有關ADI公司的定點和浮點DSP架構的信息,這是這些文章的主要主題。下一篇文章將涵蓋以下領域:
信號處理的數學概述:它將介紹整個系列中出現的變換函數(頻域)和卷積函數(時域)的數學原理。雖然數學處理必然是不完整的(沒有推導),但將有足夠的細節來考慮如何對操作進行編程。
數字信號處理器架構:本文將討論DSP的算術邏輯單元(ALU)、乘法累加器(MAC)、桶移器和存儲器總線的性質和功能,并描述支持DSP功能的數值運算。
DSP編程概念:對編程的討論將把理論和實踐(數學和建筑)結合在一起。最后,它將列出串聯長度DSP設計項目的主要參數,作為示例提供。
審核編輯:郭婷
-
處理器
+關注
關注
68文章
19178瀏覽量
229200 -
dsp
+關注
關注
552文章
7962瀏覽量
348308 -
濾波器
+關注
關注
160文章
7749瀏覽量
177735
發布評論請先 登錄
相關推薦
DSP數字信號處理簡述
數字信號處理:DSP系統設計入門課程




 數字信號處理:DSP系統設計入門課程
數字信號處理:DSP系統設計入門課程










評論