在本系列的部分中,我們討論了質量-彈簧-阻尼器(或質量-阻尼器-彈簧)結構可用于測量加速度。為了使質量塊位移與施加的加速度成正比,應適當選擇質量塊-彈簧-阻尼器系統的不同參數。本文將使用經典力學的概念推導質量-彈簧-阻尼系統的傳遞函數。
傳遞函數使我們能夠描述質量塊如何響應外部加速度而移動。在解釋加速度計的不同參數(例如傳感器線性工作范圍和帶寬規格)時,將在本系列的后續文章中使用導出的傳遞函數。
然而,在嘗試推導傳感器傳遞函數之前,讓我們簡要介紹一下微機電系統 (MEMS) 技術,該技術使當今的小型低成本慣性傳感器成為可能。
MEMS 加速度計:使用質量彈簧阻尼器結構測量加速度
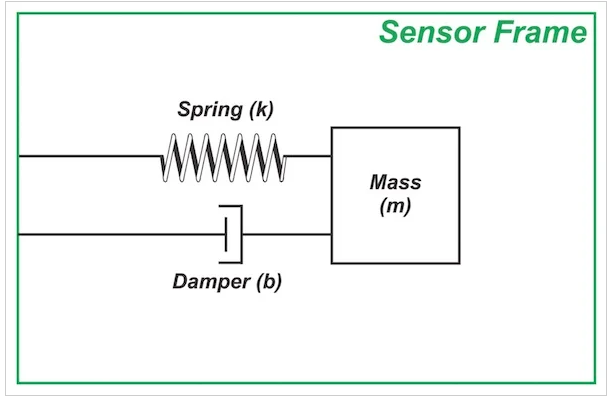
用于感測加速度的質量-彈簧-阻尼器結構如圖 1 所示。
MEMS 技術使我們能夠在同一硅芯片上實現該機械系統的非常小版本以及所需的信號調節電子設備,從而擁有完整的傳感解決方案。
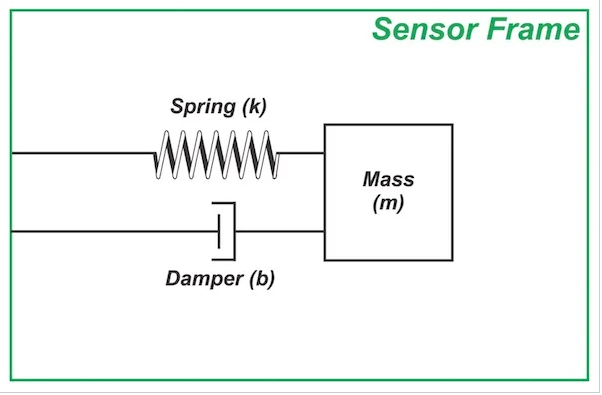
圖 1. 質量-彈簧-阻尼器結構。
MEMS 技術借鑒了微電子行業的基于光刻的微加工技術,并將它們與其他專門的制造技術相結合,從而能夠在硅芯片上創建可移動部件。
微制造技術的進步幫助實現了今天的小型、低成本微機械加速度計,圖 2 顯示了一個示例。

圖 2. CMOS MEMS 加速度計的掃描電子顯微照片 (SEM)。圖片由K. Zhang提供
在上一篇文章中,我們簡要提到了阻尼器在加速度計操作中起著至關重要的作用。在嘗試推導質量-彈簧-阻尼器系統的傳遞函數之前,現在是進一步熟悉系統的這一重要部分的好時機。
MEMS 加速度計中的阻尼機制
阻尼器模擬耗散力,該耗散力會減少質量-彈簧-阻尼器系統的機械能并減慢檢驗質量的運動。
MEMS 加速度計中的主要阻尼機制之一是運動質量與周圍空氣分子之間發生的內部摩擦。事實上,可以在極低的壓力下封裝基于 MEMS 的加速度計,以減少空氣阻尼的影響。然而,一般而言,空氣阻尼是 MEMS 加速度計中能量損失的主要。
其他常見的阻尼源是結構阻尼和熱阻尼。
結構阻尼考慮了由 MEMS 器件中使用的組件結構引起的能量損失。
熱阻尼對應于 MEMS 結構的應力-應變關系隨溫度變化的偏差。阻尼器施加在驗證質量上的總減速力通常建模為與驗證質量的速度成比例的力。
該力的作用方向與質量運動相反,由下式給出:
[F_{阻尼器} = bv ]
其中 b 表示阻尼系數,v 表示質量塊的速度。
請注意,當物體非常小時,空氣阻力與物體的速度成正比,微加工結構就是這種情況。
一般來說,空氣阻力與 物體的速度有著復雜的關系。例如,一個大物體,例如在空中移動的跳傘者,會受到與物體速度的平方成正比的阻力。
阻尼效應:需要還是討厭?
由于阻尼源自耗散力,因此它可能看起來是一種應該避免的麻煩。事實上,許多 MEMS 加速度計設計為只有少量阻尼(以降低系統的噪聲)。
但需要注意的是,沒有阻尼的理想質量彈簧系統實際上是一個振蕩器,不能用作加速度計。
如果我們將“理想”彈簧質量系統的質量從平衡狀態移開然后釋放它,即使沒有向系統施加外部加速度,質量也會永遠來回運動。這就是為什么對于加速度計,我們需要至少向彈簧質量系統引入少量阻尼。
使用牛頓運動定律證明質量位移
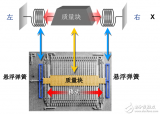
假設如圖 3 所示,外力作用于傳感器框架。
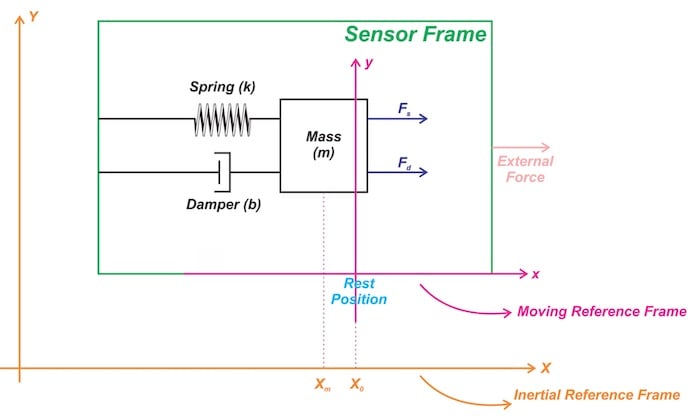
圖 3. 對外力作出反應的質量-彈簧-阻尼器結構傳感器框架。
為了根據施加的加速度計算質量塊位移,我們使用牛頓第二運動定律。正如您可能知道的那樣,該定律指出,合力產生的物體加速度與合力的大小成正比,與物體的質量成反比。
這由以下熟悉的等式表示:
[F=馬]
公式 1
其中 F 是施加在身體上的合力,m 是身體的質量,a 表示加速度。
要將此等式正確地應用到我們的系統,這里應該注意一個微妙的點。牛頓第二運動定律只適用于慣性坐標系,即不加速的坐標系。
圖 3 描繪了我們的加速度計的兩個不同坐標系。橙色坐標系對應于在解決物理問題時假定為慣性的地球參考系。
然而,品紅色坐標系表示固定到傳感器框架的參考系。
該坐標系是非慣性的,因為當向傳感器施加外力時它會加速。因此,要找到質量塊的運動方程,我們應該使用慣性參考系(橙色坐標系)。
什么力作用于證明質量?
假設如圖3所示,X 0和X m分別表示質量塊的靜止位置和任意時刻質量塊的位置。在正 X 方向的外力作用下,傳感器框架向右加速。初,質量塊由于其慣性而傾向于“后退”。這會改變檢測質量相對于傳感器框架的相對位置,并將彈簧壓縮 X 0 – X m。壓縮的彈簧對質量塊施加力并將其向右推。
彈簧施加的力由下式給出:
[F_s = k (X_0 - X_m) ]
公式 2
當質量塊偏離平衡時,阻尼器施加一個與質量塊相對于靜止位置的相對速度成正比的力,我們得到:
[F_d = b (dot X_0 - dot X_m) ]
公式 3
在上面的等式中,點符號用于顯示變量相對于時間的一階導數。請注意,位置的導數是速度。
應用等式 1,我們得到:
[F_s + F_d = ma_{證明質量} ]
代入等式 2 和 3,我們得到
[ k (X_0 - X_m) + b (dot X_0 - dot X_m) = m ddot X_m ]
方程式 4
在這個等式中,雙點符號表示 X m相對于時間的二階導數。請注意,? m是驗證質量的加速度。
求非慣性參考系中的運動方程
需要根據質量塊從其平衡位置的位移來重寫方程式 4。這是因為我們在實踐中的傳感方法測量的是質量塊偏離其平衡狀態的位移。
例如,如圖 4 所示,電容式感應方法測量檢測質量塊相對于靜止位置的位移。
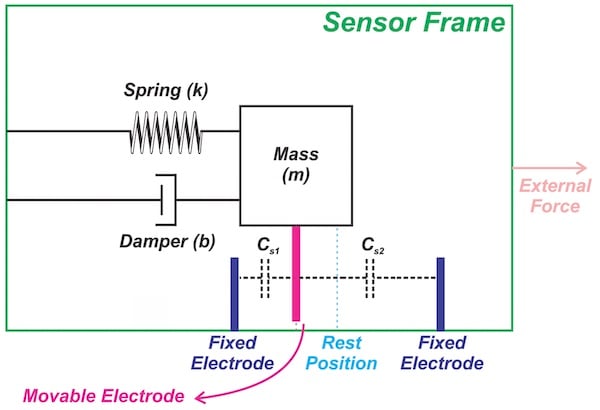
圖 4.通過電容感應測量質量塊位移的設置 。有關更多信息,請查看本系列的上一篇文章。
為了根據質量位移來表達方程式 4,我們需要使用圖 3 中洋紅色坐標系所示的移動參考系。我們使用小寫字母 x 和 y 表示該坐標系。
如您所見,驗證質量位移由 X m – X 0 = x給出。
在這種情況下,公式 4 簡化為:
[ -kx - b dot x = m ( ddot X_0 + ddot x) ]
由于 ? 0 是傳感器坐標系上的一個不動點,它的二階導數等于傳感器坐標系 a 的加速度。這其實就是我們要衡量的參數。
因此,上述等式導致:
[ m ddot x + b dot x + kx = -ma ]
尋找傳遞函數
應用拉普拉斯變換,我們可以找到加速度計的傳遞函數為:
[ H(s) = frac{x(s)}{a(s)} = frac{-1}{s^2 + frac{b}{m}s + frac{k}{m }} ]
這是一個二階系統。根據系統參數的值,即 m、k 和 b,系統響應將不同。
例如,如果傳感器幀加速度突然從零變為有限值(階躍輸入),則系統的輸出將接近其終值,其時間響應特性由系統參數確定。
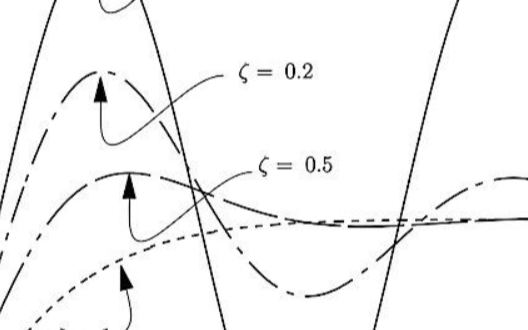
圖 5 顯示了改變系統參數如何改變輸出的振鈴和穩定時間。在我們的討論中,輸出是證明質量位移。
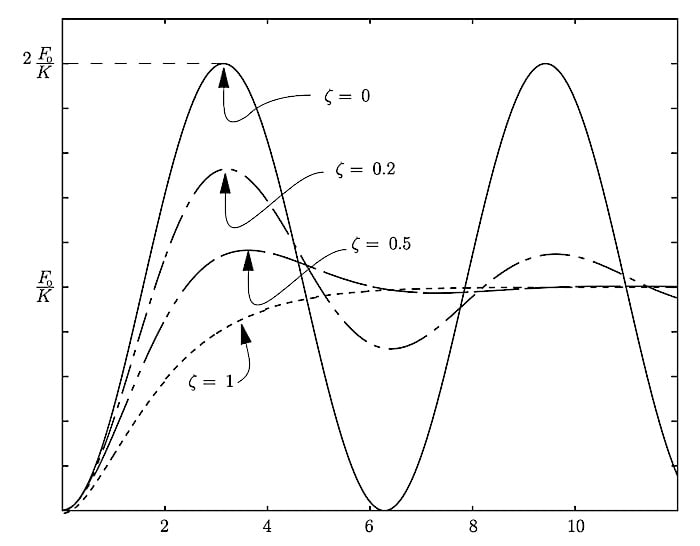
圖 5.二階系統的階躍響應會根據系統參數的值發生顯著變化。圖片由麻省理工學院 David L. Trumper提供
在下一篇文章中,我們將使用導出的傳遞函數來討論一些重要的系統參數,例如傳感器線性工作范圍、響應誤差和帶寬。
-
mems
+關注
關注
129文章
3896瀏覽量
190340 -
加速度計
+關注
關注
6文章
698瀏覽量
45858
發布評論請先 登錄
相關推薦
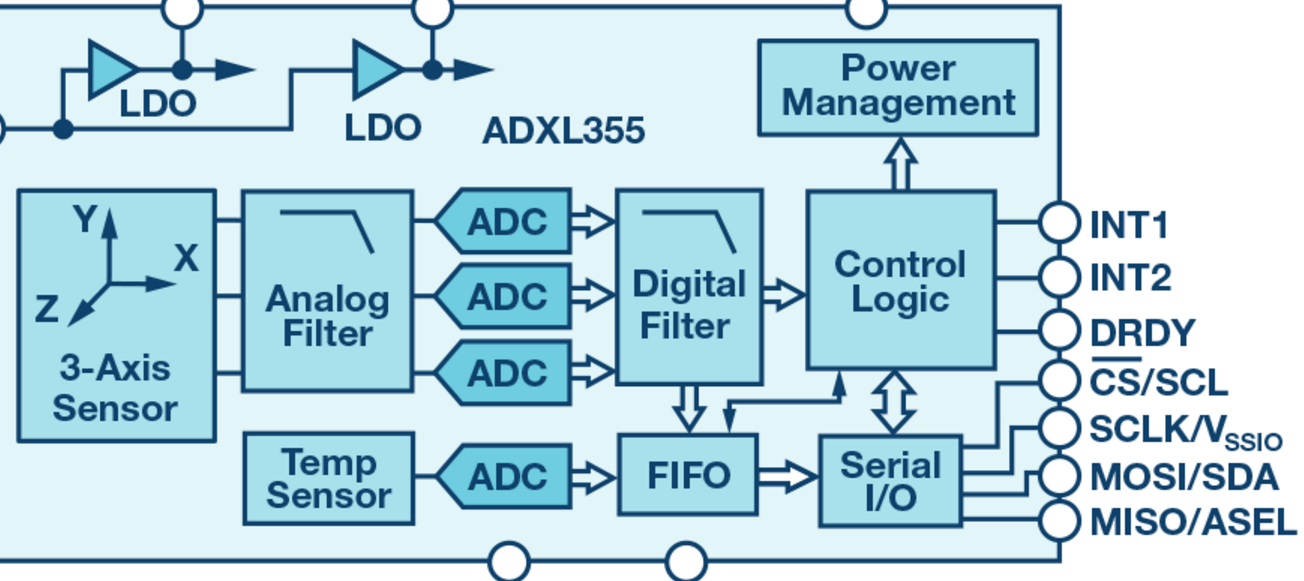
基于ADI的MEMS加速度計關鍵參數和特性,選出最適合你的MEMS加速度計




 推導電容傳感加速度計的傳遞函數
推導電容傳感加速度計的傳遞函數










評論