實際上的系統都是非線性的。

但是對非線性系統的分析，比對線性系統的分析，要復雜。

所以，在一些特定的條件下，就假設系統是線性的，比如說當輸入信號很小的時候，我們可以假設放大器是線性的。

but，非線性其實一直都存在的。

比如說，對于一個RF接收機，當只有微小的小信號的時候，我們可以把他近似為線性系統。

但是如果有大的干擾信號進來，它就會有非線性行為。

一個無記憶的非線性系統，可以用下式表示。所謂無記憶系統，是指其輸出，主要取決于當前的輸入x(t)，而和以前的輸入無關。

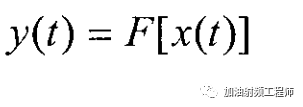
然后，將上式中的右邊展開為一個冪級數，如下圖所示。

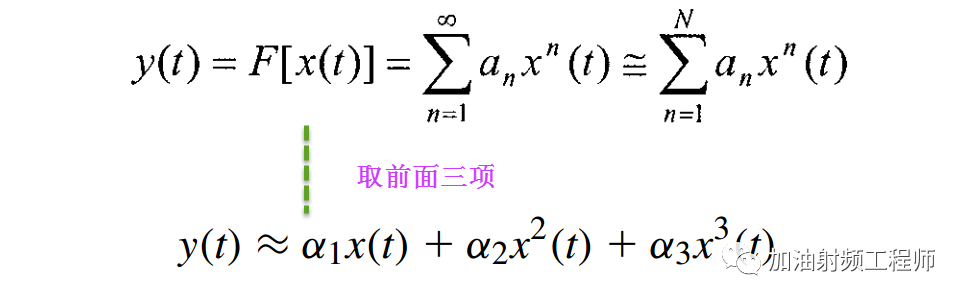
假設輸入信號x(t)中包括三部分，分別為：

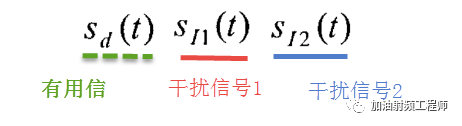
于是，非線性系統的輸入y(t)為：

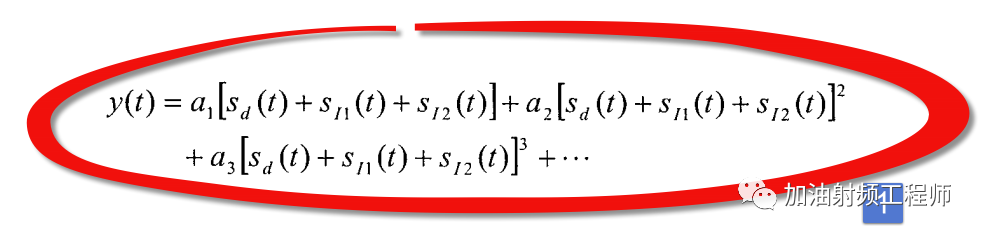
就是從這個式子，可以讓我們觀察到多種不同的非線性響應。

情況1：

增益壓縮和Desensitization

增益壓縮呢，就是指當有用信號功率增大時，系統的增益會呈現壓縮的現象。

Desensitization，也是一種增益壓縮，只不過是因為干擾信號的功率增大，導致系統的增益出現壓縮，從而使得有用信號的增益下降，出現阻塞的現象。

假設有用信號為單音信號，頻率為f0；干擾信號也為單音信號，頻率為f1；另一個干擾信號為0，如下圖所示。

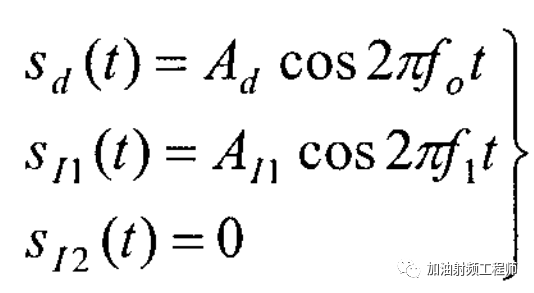
代入上式（1），可以得到：

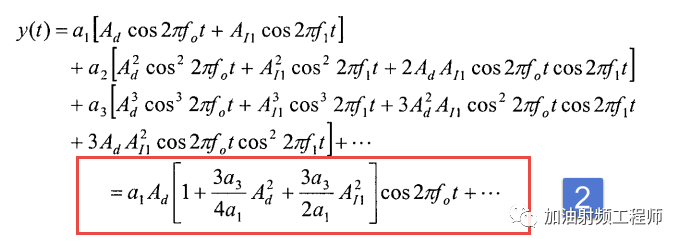
現在來對式2進行較為深度的剖析。

case1:

當干擾信號沒有，且有用信號的幅度很小(Ad<<1)時，上式（2）可以簡化為：

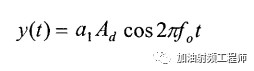
因此，此時系統的小信號增益為a1，這時的系統，近似為一個線性系統。

case2:

有用信號的幅度開始變大(干擾信號還是假設沒有)，此時系統的增益開始隨著信號功率的變化而變化。

式2中括號里的第二項：

變得不能忽略。

如果a3的符號與a1的相反，那么隨著信號功率的增加，系統增益變小。

這種現象稱為增益壓縮(gain compression).

此時，增益大小如下式所示。

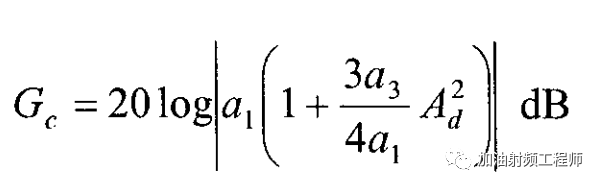
當增益比小信號增益下降1dB時，此時的輸入功率，被稱為輸入1dB壓縮點。

因此可以得到：

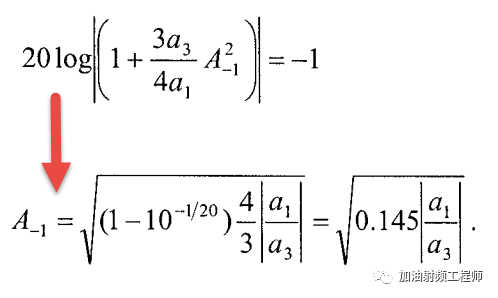
case3:

現在考慮上干擾信號，當a3<0時，如果干擾信號的幅度升高，系統的增益也會下降。

從式2中可知，干擾信號導致增益下降的幅度為：

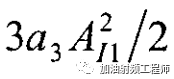
這種非線性現象，稱為desensitization.

所以，當干擾足夠強的時候，可能會導致系統的增益下降到0，此時有用信號的增益就是0，那么有用信號將會被完全阻塞。

情況2：

交調(crossmodulation)

如果輸入信號x(t)包括一個小幅度的有用單音信號和一個強干擾信號，且該強干擾信號上有幅度調制，即：

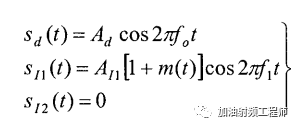
該非線性系統的輸出變為：

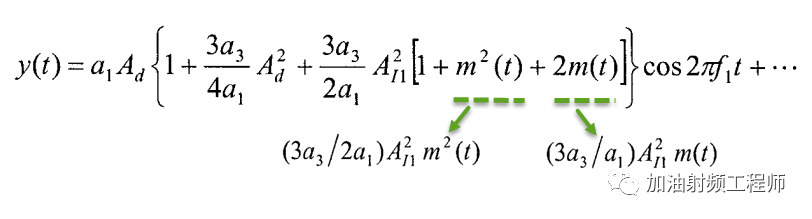
可見，除了desensitization和增益壓縮項外，還有兩個新增的項。

這些新的項，則表示強干擾信號上的幅度調制，由于系統的非線性特性，被轉移到有用信號上了。

這種非線性現象稱為交調(crossmodulation).

情況3：

互調(intermodulation)

現在考慮輸入信號x(t)中，除了有用信號外，還有兩個干擾信號，并假設他們都是單音信號，即：

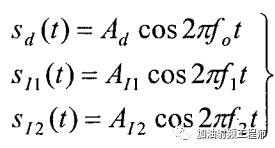
所以，可以得到：

在上式中，頻率(f1±f2)的項，稱為二階互調產物；頻率(2f1±f2)和(2f2±f1)的項為三階互調產物。

這種非線性現象稱為互調(intermodulation).

審核編輯：劉清