一、為什么要進行攝像機標定

隨著機器視覺的迅猛發展，我們已經不滿足于使用攝像機進行監控、抓拍這種較為簡單的功能。更多的用戶青睞于它在非接觸三維尺寸測量上的應用。我們所謂的三維測量是廣義的三維測量，它不僅包括三維物體的重構與測量，還包括在三維空間中識別任意二維平面上的尺寸以及位置。這種技術目前已被應用在高精度的工業模具以及裝配測量中，其中任意二維平面上的尺寸檢測技術應用得更為廣泛。

圖一

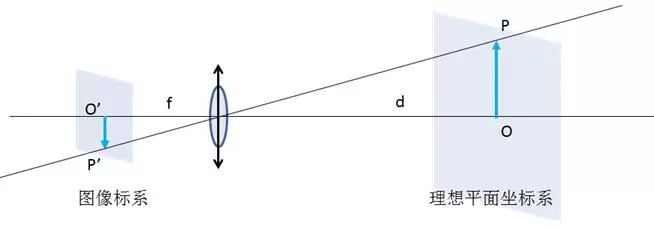
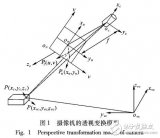
如圖1當被測平面和像平面平行且成像模型為理想的小孔成像模型，我們設焦距為f、工作距離為d，則被測物OP和它的像O’P’關系可簡單的表示為：

|OP|=|O’P’|×d/f 【1】

但是在實際應用中并非如此，我們無法嚴格控制像平面和被測平面的位置，所用的鏡頭也不是嚴格的小孔模型。如果直接使用【1】式計算將會產生極大的誤差。因此，為了獲取更高的測量精度，我們需要通過標定來實現坐標平面的轉換以及圖像的校正。

二、什么是攝像機標定

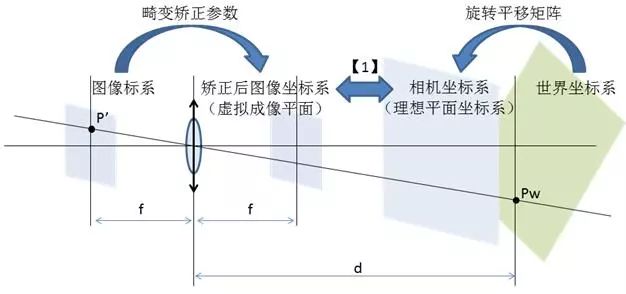
在實際應用中，被測平面的不確定性以及鏡頭的畸變使我們已經無法簡單的使用【1】式計算出實際距離，但是我們可以將目前能夠獲得的數據進行轉換，使這些數據符合【1】式的使用條件。也就是將任意坐標平面通過旋轉和平移映射到理想坐標平面上，對有畸變的圖像進行校正，讓它成為符合小孔成像模型的像平面。有了這種方法，我們只要確定轉換算法、校正算法以及【1】式中的參數就可以實現三維空間中任意平面上尺寸與位置的測量。我們將這種確定參數的過程稱之為標定。

三、攝像機單目標定

攝像機標定的方法根據攝像機的數目可分為單目標定、雙目標定以及多目標定。其中單目攝像機標定是雙目標定的基礎，而多目攝像機的標定則是雙目攝像機的擴展。因此，我們今天首先來為大家介紹單目標定。在平面測量中影響我們拍攝圖像形變的因素有兩個：鏡頭和攝像機的姿態。根據這兩個因素我們將攝像機的參數分為兩組，攝像機內參和攝像機外參。

1、攝像機內參

內參一般包括鏡頭的焦距f、鏡頭畸變參數k、光軸中心坐標(Cx,Cy)以及像元尺寸Sx,Sy，當攝像機和鏡頭確定時，這些參數唯一確定。下面我們來詳細介紹一下各參數的數學模型。

1)焦距

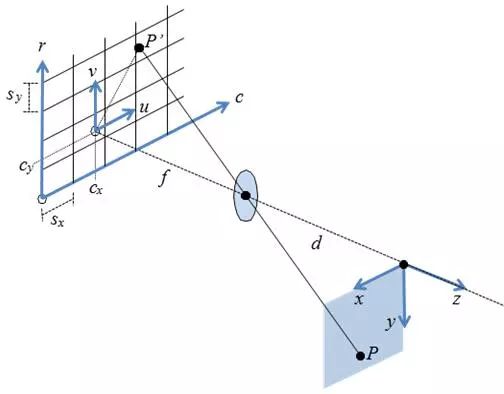
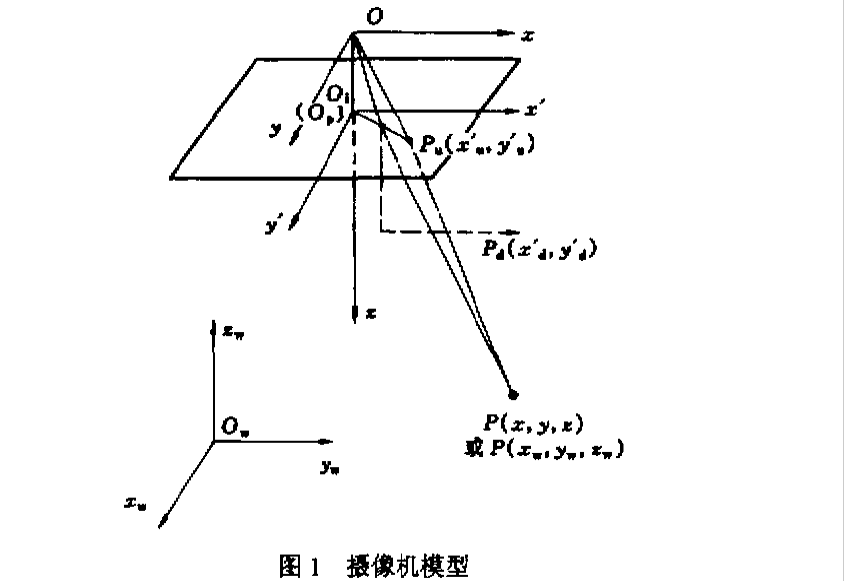
根據鏡頭類型不同焦距的計算可分為針孔模型和遠心模型。如圖3我們假設世界坐標系有任一點P(x,y)，在攝像機靶面所成的像為P’(u,v)，根據不同的光路模型它們之間有如下的對應關系

a) 針孔模型

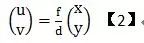
b)遠心模型

由于遠心鏡頭特殊的光路設計使得像的大小與拍攝距離無關，因此表達式比針孔模型更為簡單。

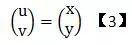
2)鏡頭畸變

受到鏡頭的制作和安裝精度的影響，我們所獲得圖像會產生非線性失真。我們稱這種失真為鏡頭畸變。鏡頭畸變產生的誤差使得理想針孔模型已不再適用。因此我們需要先將所得圖像進行校正，再應用理想的針孔模型。假設我們所獲取的原始圖像坐標(u,v)、校正后的結果(u’,v’)，其畸變模型坐標關系為：

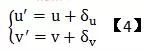
a)徑向畸變

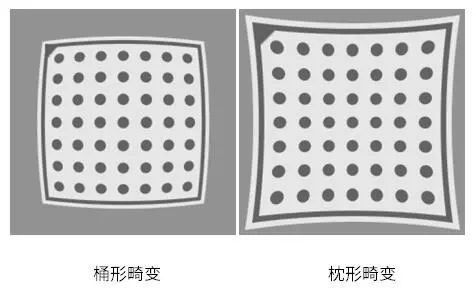
徑向畸變主要由透鏡制作過程中表面曲率引起，它會使圖像發生桶形畸變和枕形畸變（如圖4）。其數學模型如下：

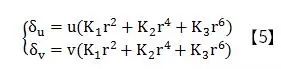
其中，如果對精度要求不是很高我們可以令將上式簡化為如下表達式：

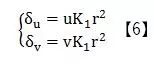
b)離心畸變

離心變量又稱偏心變量，它的誤差來源于透鏡的安裝精度，這主要是因為所有鏡片的光學中心并不能嚴格的保證在同一條直線上。這種誤差除了在引入徑向畸變同時還會引入切向畸變。由于之前我們已經進行了徑向畸變的校正，因此我們在此基礎上只需加入切向畸變校正即可。其數學模型如下：

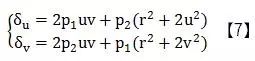
c)薄棱鏡畸變

影響薄棱鏡畸變的主要因素的是透鏡以及攝像機靶面的平行度，鏡片與攝像機靶面夾角越大畸變就越嚴重。其數學表達式如下：

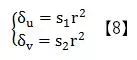
d)畸變校正

在實際的應用中，大多數工業攝像機的廠商可以通過攝像機接口螺紋的機械精度來保證鏡頭透鏡與靶面的平行性，而且這種畸變產生的誤差較小，因此在一般的圖像標定中不作考慮。至此，我們已經基本掌握了大多數情況下畸變產生的原因以及數學模型。結合【5】、【7】兩式我們可以推導出鏡頭畸變校正模型：

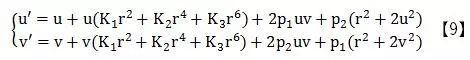
2. 攝像機外參

攝像機的外參是指攝像機坐標系與世界坐標系的轉換參數它主要由旋轉矩陣R和平移矩陣T組成。對于任意三維坐標系，我們都可以通過這兩個矩陣將其轉換到攝像機坐標系中。其數學模型為【10】

1)旋轉矩陣R

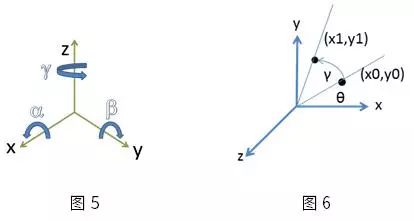
如圖5所示，我們通過沿坐標軸x、y、z分別旋轉α、β、γ來實現坐標系的轉換。因此，旋轉矩陣R可分解為Rx（α）、Ry（β）、Rz（γ）三個矩陣相乘的形式。我們以z軸為例，假設(x0,y0)與x軸夾角為θ，且到原點距離為r，通過旋轉矩陣

Rz（γ）坐標系沿z軸旋轉γ后得到點(x1,y1)，我們可得方程組:

x1=r·cos(θ+γ) 【11】

y1=r·sin(θ+γ) 【12】

由三角函數展開得:

x1= r·cos(θ) cos(γ)- r·sin(θ) sin(γ) 【13】

y1= r·sin(θ) cos(γ)+ r·cos(θ) sin(γ) 【14】

由(x0,y0)與x軸夾角為θ得：

x0=r·cos(θ) 【15】

y0=r·sin(θ) 【16】

將【15】式帶入【13】式、【16】式帶入【14】式得：

x1=x0·cos(γ)-y0·sin(γ) 【17】

y1=y0·cos(γ)+x0·sin(γ) 【18】

因此

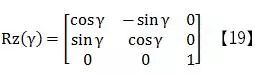
以此類推求得Rx（α）和Ry（β）將它們與Rz（γ）相乘得：

2)平移矩陣T

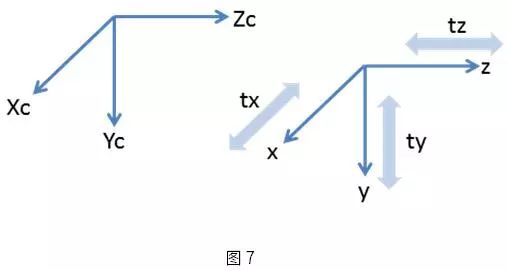
通過旋轉矩陣運算后，世界坐標系的三個坐標軸會與攝像機坐標系對應的坐標軸相平行。此時我們已經離我們的目標又近了一步。如圖7所示我們現在只要沿各坐標軸做平移運算即可，由此得：

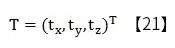
3)參數求解

根據【2】、【9】、【20】、【21】這幾個數學模型，我們可以得知，若想確定一個攝像機與被測平面的相對位置，則需要確定包括內參、外參在內的14個參數，其中是已知的。因此，我們至少需要9個坐標點，構成9個方程才可以解出剩余的9個未知數。在通常情況下，點的分布以覆蓋大部分視場為準，獲得的數據點越多，統計的參數就越準確。我們一般采用最小二乘法或者線性規劃等統計算法來求解相應參數。下面我們以HALCON為例演示一個標定的全過程。

HALCON是德國MVTEC Software GmbH公司開發的一套完善的機器視覺算法軟件包。它除了擁有亞像素精度的算法以及高效的處理性能外，在三維重構方面它也有卓越的表現。它的開發環境中自帶攝像機標定工具，可以輕松的完成攝像機的標定工作。同時，您還可以使用HALCON生成可打印的標定板文件。下面我們就來介紹一下攝像機標定的整個流程。

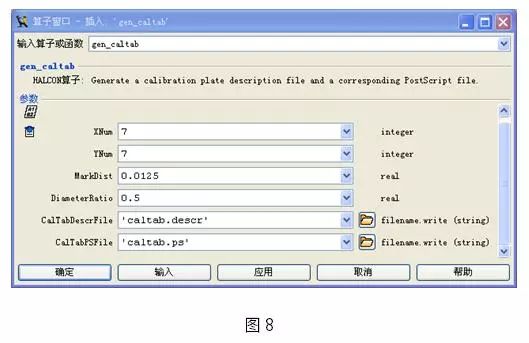
a)生成標定板

i. 創建標定板

使用HALCON開發環境HDevelop創建標定板

在選擇尺寸選擇時推薦大家使用邊長為視野1/3左右的標定板

ii.打印標定板

通過GSView等高精度打印軟件打印標定板。

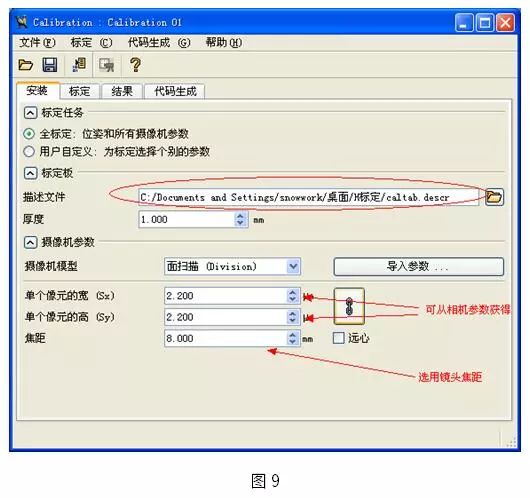
b) 攝像機參數設置

輸入所使用的攝像機以及鏡頭的相關參數

c)拍攝標定板圖像

我們采用平移和傾斜的方式使得拍攝圖像中的標定板盡量覆蓋整個視場。

一般情況我們需要保存15幅不同位置的圖像，具體位置如下：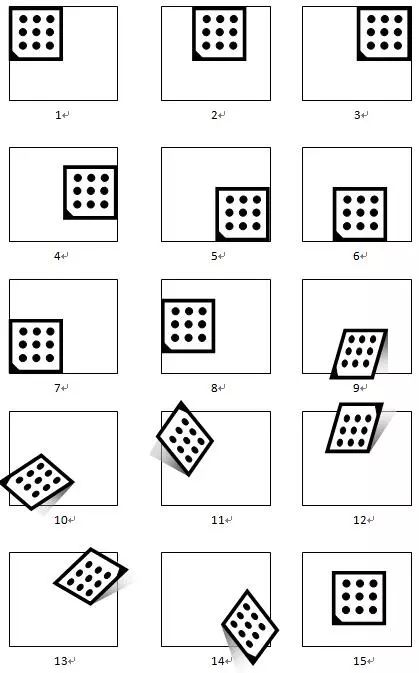

d)標定圖像載入

通過HALCON我們可以實時拍攝圖像也可以讀取我們事先拍攝好的圖像進行標定。如果標定板識別成功，圖像上將繪制出標定板坐標系。

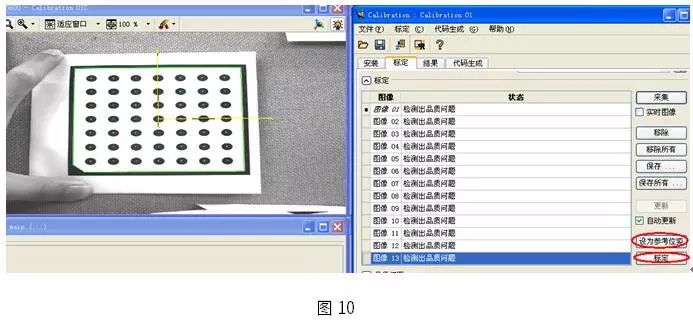
e)標定

標定后我們會獲得攝像機內參和外參。我們還可以將它們保存起來用于坐標轉換或圖像校正。

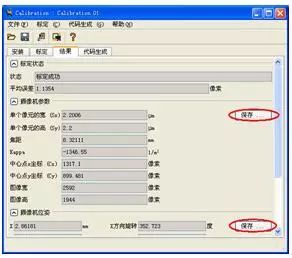
f)驗證標定結果

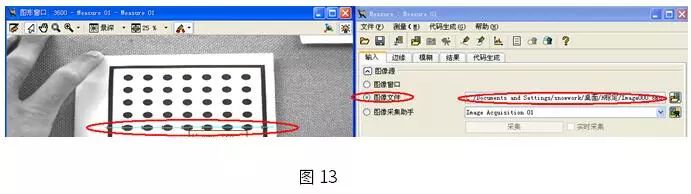
在HALCON中不僅有攝像機標定工具還有測量工具，下面我們使用HDevelop自帶的一維測量助手來驗證一下我們的標定結果。

首先我們要加載我們剛才標定的數據。

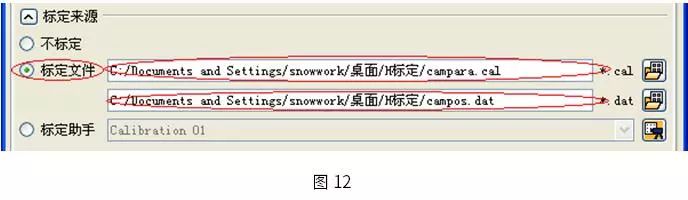
成功加載標定數據后我們就可以使用我們隨機拍攝的一張圖像進行測量。

通過以上幾步操作，現在我們就已經得到了像素點的實際距離。

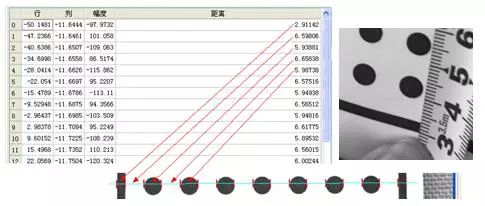
復雜的標定工作在HALCON的幫助下就輕松的完成了。不僅如此，以上的所有步驟都可以導出為代碼，我們可以將這些代碼集成到我們自己的程序中。

備注：若采用高精度的標定板將會得到更高精度的標定結果。

四、應用

單目攝像機標定技術適用于被測表面曲率較小且需要獲取實際數據的應用場合，比如食品、機械制造以及半導體等。理論上，在檢測過程中所有的被測物尺寸的判斷都可以使用像素尺寸來完成。雖然像素尺寸和實際尺寸對于計算機來說幾乎是一樣的，一般只用于比較大小，但是對于我們來說實際尺寸更加直觀。

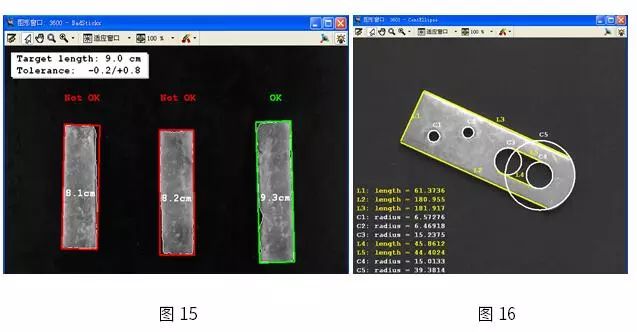
圖15 圖16

圖15為速凍魚柳檢測系統的圖像處理示例。由于實際應用中不同批次的魚柳寬度不同，因此，最好的辦法是使用標定后獲取的實際數據來進行計算。這種判定方法使得系統參數更加直觀，設置更加方便。圖16為工件尺寸檢測系統，通過標定，我們不僅可以獲取實際數據，而且可以將它們直接和CAD中數據進行比較，提高檢測效率。

五、結語

在機器視覺產業的蓬勃發展的今天，攝像機標定已經逐步應用到醫療、食品、磨具生產、半導體生產等諸多檢測系統中。隨著像HALCON這樣的算法庫用戶群的不斷擴大，攝像機標定在作為我們研究課題的同時，也會不斷的走進工業應用中。它將為我們提供更完善，更精準的二維以及三維空間的解決方案，成為提高工業生產效率和產品質量的推動力。
責任編輯：彭菁