Max-Cut問題簡單地說，就是求一種分割方法。給定一張無向圖, 將所有頂點分割成兩群, 同時使得被切斷的邊數量最大，或邊的權重最大。

QUBO（Quadratic Unconstrained Binary Optimization）問題即二次無約束二值優化問題，將一個傳統問題轉為QUBO問題建模需要重點關注三部分：

①把建模對象中的變量映射為binary（0/1或者-1/+1）的變量；

②原模型的約束條件需要“處理”到目標函數中，成為無約束問題；

③模型變量的最高次不超過二次。

我們先從簡單的問題開始說明，讓大家有些直觀感受。Max-Cut問題就是一個非常簡單，并容易理解的例子。同時Max-Cut問題無需復雜的操作，其模型本身就是QUBO問題。

最大割問題是一類NP難問題，它在計算機科學和組合優化領域中有著廣泛的應用。在量子計算領域，最大割問題是一個非常重要的Benchmark，因為它是量子計算機中最具代表性的NP難問題之一，也是許多量子算法的基礎。同時，最大割問題在實際應用中有著廣泛的應用，如社交網絡分析、電路設計、圖像分割等領域。因此，通過研究量子算法解決最大割問題，可以為這些領域提供更高效的解決方案。

在量子計算行業中，不同公司往往將Max-Cut問題作為基礎案例進行測試，用于算力的對比測試，而經典計算中的很多代表性企業等都曾使用Max-Cut來做新品算力的標定。如英偉達公司使用 896 個 GPU 模擬 1688 個量子比特，能夠處理包含高達 3375 個頂點的圖最大割問題，Quantinuum 研究團隊通過在20量子比特的Quantinuum H1-1量子處理器上進行實驗，可解決80個頂點的最大割問題。

2023年5月16日，北京玻色量子科技有限公司（以下簡稱“玻色量子”）的CTO魏海博士在首場新品發布會現場，就提出了Max-Cut是實用量子計算的“算力標準”。

Max-Cut問題是實用量子計算的“算力標準”

魏海博士提到，在實際問題求解中，玻色量子自研的相干光量子計算機真機——“天工量子大腦”，適用于高效求解組合優化問題，其中最具代表性的21個NP-Complete模型（簡稱“NPC”）在我們的生活中無處不在。這些問題之間可以互相歸約轉化，技術中經常用Max-Cut問題來做統一的數學表達，表征計算復雜度。因此，為了標定量子計算的算力優勢，我們采用在經典計算中和量子計算中都通用的Max-Cut問題來作為實用量子計算的“算力標準”。

那么，為了更清楚的理解最大割問題，并徹底揭開它的“神秘面紗”，下面將通過案例對該問題在模型層面進行全面解讀。

問題描述

最大割問題是NP完備問題。給定一張圖, 求一種分割方法, 將所有頂點分割成兩群, 同時使得被切斷的邊數量最大，或邊的權重最大。

由于二元變量存在（0/1或者-1/+1）表達形式的區別，常見模型有兩種建模思路，在這里分別進行說明。

建模思路一

在無向圖G（V,E）中，V為網絡的頂點集合，E為網絡的邊集，其中點i,j∈V，（i,j）∈E，wij為頂點i,j間的邊的鄰接矩陣，有連邊關系則取1,無連邊關系則取0。決策變量σi，σj表示頂點i,j的分類，其可能的取值為{1,-1}，我們將V劃分為A、B兩類。

則在給定的無向圖中，將所有頂點分割成兩群的分割方法所對應割取的邊的個數為Z，模型表示為:

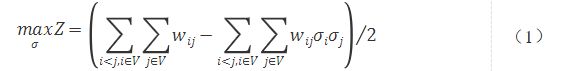
式（1）即為Max-Cut最大割問題模型，同時其也是QUBO模型。

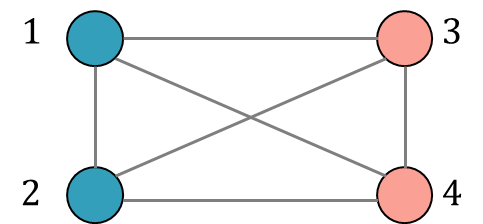
圖1：Max-Cut問題實例為描述該案例，本文以一個四節點實例說明，如圖1所示，通過觀察我們發現將1、2分為A類，3、4分為B類的“割”法將得到問題的最優解4，如圖2所示，下面我們對這個案例進行分析。

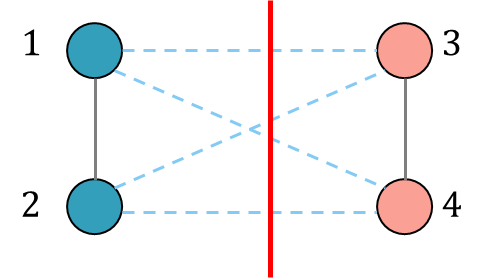
圖2：Max-Cut問題“割取”示意

通過連邊關系可知

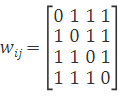
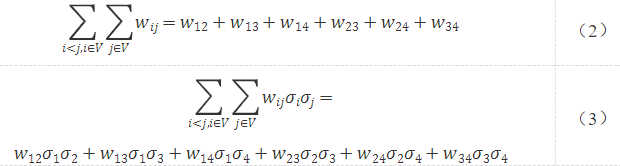
當點1、2為一組，點3、4為一組時，σ1=σ2=1，σ3=σ4=-1。 則式（3）變為

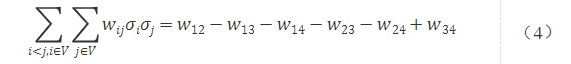
結合式（1）、（2）和（4）可得

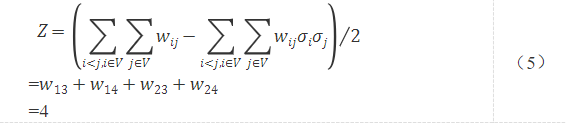
圖1的最大割數量為4，符合我們的設想。

當然，這個問題還可以簡化，細心的朋友發現wij為系數矩陣，并不影響模型的計算，所以模型式（1）可以轉換為求解式（6），式（1）與式（6）在解的取值上是等價的。

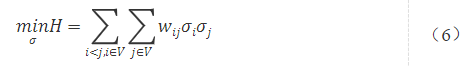
同時，式（6）也被理解為一種Ising模型的表達方式。

在該建模思路下，式（1）與式（6）均可理解為Max-Cut最大割問題模型，同時其也是QUBO模型。不同的是，式（1）的目標函數可以表示為割去的邊的個數，式（6）的目標函數常用于表示為哈密頓量。

建模思路二

思路1中二元變量通過-1/+1表示，同樣我們可以通過0/1變量構建模型，我們用變量xi表示頂點i屬于A,B中的某一類。

則在給定的無向圖中，將所有頂點分割成兩群的分割方法所對應割取的邊的個數為Z，模型表示為:

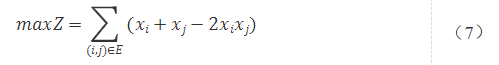
在該建模思路下，式（7）為Max-Cut最大割問題模型，同時其也是QUBO模型。式（7）與式（1）的目標函數可以表示為割去的邊的個數。 我們可以試著用QUBO的矩陣表達來描述這個案例。 首先，式（7）等價于式（8）

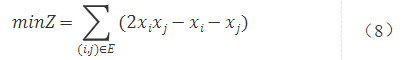
QUBO的矩陣表達式為

其中，線性項決定了矩陣Q的主對角線上的元素，二次項決定了非對角線上的元素。

以圖1中的4節點，6條邊的案例為例

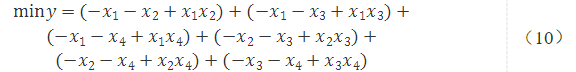
簡化后可得

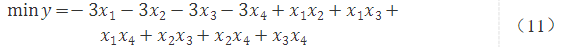
則Q矩陣表達為

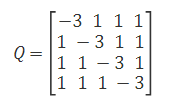
解決這個QUBO模型可以得到x={1,1,0,0}。因此頂點1和2在一個集合中，頂點3和4在另一個集合中，最大切割值為4。

問題拓展

有一個更普遍的問題版本稱為加權Max-Cut。在這個問題中，每個邊都有一個權重系數，目標函數由最大化邊的個數調整為邊的總權重之和。

在上述例子中，問題特征直接自然構建了QUBO形式的優化問題。但許多其他問題需要“重鑄”來創建所需的QUBO形式。我們將在后面繼續介紹其他問題的QUBO建模及其求解。