不知道大家有沒有這樣的疑問:我明明是在學“數字濾波器設計”,怎么突然冒出一個“模擬濾波器設計”來?我是不是學了個假的數字信號處理?
我們首先來解釋一下。
第一,大多數數字信號處理系統中不可避免地要用到模擬濾波器,比如:AD轉換器前的抗混疊濾波器、DA轉換器之后的平滑濾波器,都是模擬濾波器。因此,模擬濾波器設計也是數字信號處理中應當掌握的技術。
第二,我們說了,IIR濾波器設計的一種重要方法稱為“ 模擬原型法 ”,就是 首先設計模擬濾波器,然后轉換為數字濾波器 。這種方法有歷史原因的,在歷史發展的長河中,模擬濾波器先出現,幾十年之后才出現數字濾波器。在數字濾波器出現之前,模擬濾波器已經形成了一套完善的設計方法。所以人們自然而然地想法就是,先設計模擬濾波器,再轉換為數字濾波器。
這兩點,是我們把“模擬濾波器設計”的內容放在本章中學習的原因。
在正式內容開始之前,為了更好地理解,我們首先做幾點鋪墊:
第一點,本節中,因為討論對象是模擬系統,所以所涉及到的角頻率變量都是大寫的Omiga(文字中只能用W表示),即“模擬角頻率”。系統函數和頻率響應函數用Ha(s)/Ha(jW)表示(“a”為analog的第一個字母);
第二點,在本章中,我們一般只關注其幅頻特性|Ha(jW)|,因為模擬濾波器的相頻特性一般都是非線性的。
第三點,IIR濾波器的設計方法,是用一些形狀合適的數學函數,通過調節函數中的某些參數,來直接逼近濾波器的幅度函數,使其滿足性能指標的要求。其目標依然是 確定系統函數Ha(s)分子分母多項式的階數以及系數 。
第四點,上面所說的“形狀合適的數學函數”,一般是作為濾波器的 幅度平方函數 ——也就是幅度函數的平方,即|Ha(jW)|^2。有的同學可能會有疑問“為什么不直接作為幅度函數,而是幅度平方函數”,這個疑問放一放,等到下面第二個問題就明了了。
一 幅度平方函數
幅度平方函數,顧名思義,就是幅度函數的平方,也就是:|H(jW)|^2。
在這里我們要解決一個問題:已知|Ha(jW)|^2的函數表達式,如何求Ha(s)?
有的同學說了,這個簡單,把|Ha(jW)|^2開平方,得到Ha(jW),然后令jW=s,就得到Ha(s)了?
你有這樣的想法,說明你 too young too simple。首先,|Ha(jW)|^2開平方,只能得到 |Ha(jW)| 而非 Ha(jW),因為|Ha(jW)|^2不包含相位信息,也就是說,如果沒有其他限定條件,|Ha(jW)|^2不能得到唯一的Ha(s)。

那是不是說,我們開平方后得到|Ha(jW)|,然后給它配上一個我們需要的相頻函數,構造出 Ha(jW)=|Ha(jW)|e^j[fai(W)],再令 jw=s 得到 Ha(s) 就可以了呢?
這個想法,理論上說好像可以。但是實際中我們不是這樣處理的。因為我們研究的都是實系統,即ha(t)為實函數、Ha(s)為有理函數(通過多項式的加減乘除得到的函數,其系數是實數),顯然,用上面所說的方法是無法得到有理函數形式的 Ha(s) 的。
那應該怎么辦呢?我們首先從公式上推導一下 |Ha(jW)|^2 與 Ha(s) 的關系,如下式:
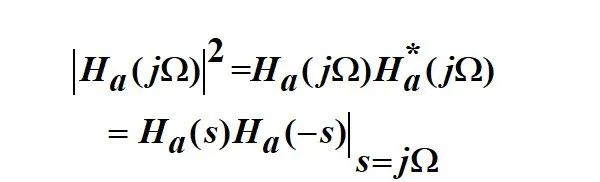
上述結論的推導過程如下:
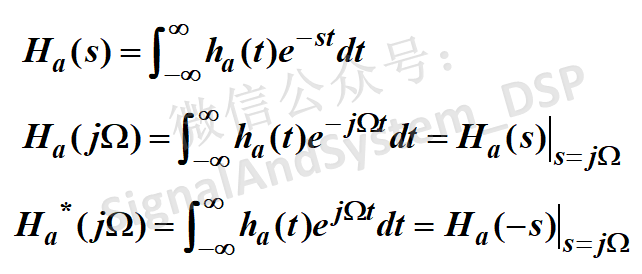
這個關系說明什么呢?
如果s0是Ha(s)的極點,那么 -s0 一定是Ha(-s) 的極點,而且,s0 和 -s0 二者都是 Ha(s)Ha(-s) 的極點。零點亦是如此。
也就是說,實系統的 幅度平方函數的極點必然共軛成對、并且以虛軸鏡像成對出現。零點也是這樣。 更通俗地說,就是:如果在實軸上,就是兩個一對,下圖中的(P5,P6);如果在虛軸上,貌似兩個一對,實則四個一對,因為是二階極(零)點,如下圖中的(A5,A6);如果既不在實軸也不在虛軸上,就是四個一對,如下圖中的(A1,A2,A3,A4)和(P1,P2,P3,P4)。
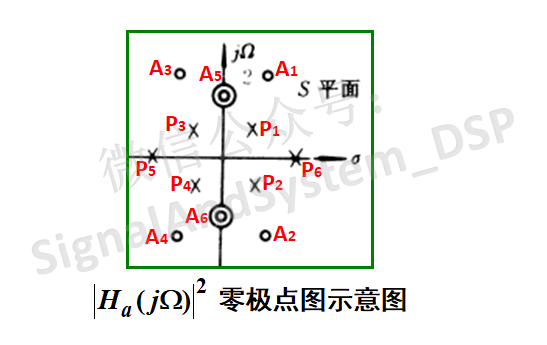
到這里,下面的問題就好辦了。我們選一半極點、一半零點給Ha(s),剩下的一半給 Ha(-s),就可以了。極點零點一旦確定,Ha(s) 有理分式的形式就可以寫出來了。
顯然,選哪些分給Ha(s)、哪些分給Ha(-s),有多種選擇方法。但是也要滿足一定的約束條件。
首先,要保證是實系統,極點和零點都必須共軛成對;第二,為了保證系統為因果穩定系統,極點只能選擇左半平面的分給Ha(s)、右半平面的分給Ha(-s),零點不影響穩定性,故不受此約束;第三,可以根據相位特性的要求,選擇一半共軛成對的零點分給Ha(s)、另外一半分給Ha(-s),例如,如果要求是最小相位系統,零點也必須位于左半平面。
解決了“由幅度平方函數得到系統函數”的問題之后,下面,我們就來看哪些數學函數適合做濾波器的幅度平方函數。我們以低通濾波器為例。
兩位大咖即將隆重登場,分別是巴特沃斯和切比雪夫。
二 巴特沃斯濾波器
1. 巴特沃斯函數
巴特沃斯是誰?英國一名普普通通的工程師,全名斯替芬·巴特沃斯(Stephen Butterworth),憑借1930年發表在英國《無線電工程》期刊的一篇論文而名垂青史。
巴特沃斯函數的表達式為:
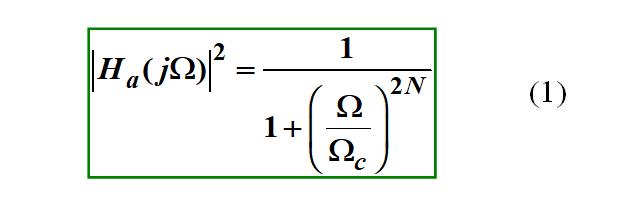
在這個表達式中,W為變量,N和Wc為常數。這個函數很簡單,但是設計的很巧妙。
我們先來認識它一下,看一看它的模樣。
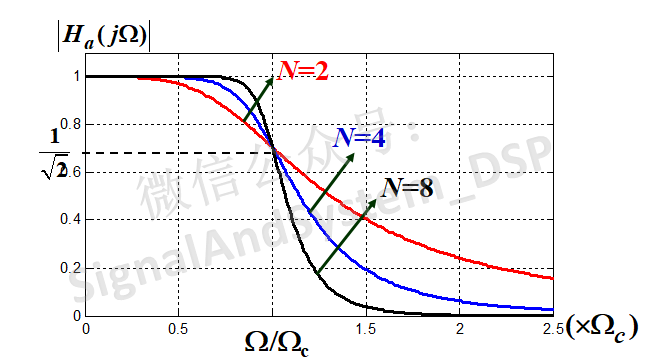
上圖是以W/Wc為橫軸、|Ha(jW)| 為縱軸畫的圖(用matlab畫的),分別畫出了N=2、N=4和N=8時的圖形。
然后,我們來分析一下它的特點:
特點一:W越大,函數值越小。而且,它的前 2N-1階導數在W=0處都為零,表明在 W=0 附近一段范圍內都是非常平直的。故“最平響應特性濾波器”的稱號它當之無愧;
特點二:N越大,通帶增益越平坦,頻帶邊緣下降越陡峭,即越接近理想性能。從上圖中也可以看出來,黑、藍、紅這三條線,顯然是黑色(N=8)時代表的濾波器性能最好;
特點三:三條線都交于一點(W=Wc)。這是顯然的,當W=Wc時,|Ha(jW)|^2=1/2,與N無關,轉換為dB就是10log(1/2)≈-3dB,所以稱 Wc 為 **3dB帶寬** 。這一特點,稱為“3dB帶寬不變性”(即與N無關);
特點四:此函數,沒有零點,故稱為全極點型濾波器。
2. 巴特沃斯函數的極點
下面,我們來求一下巴特沃斯函數的極點。
令公式中的 jW=s,得到:
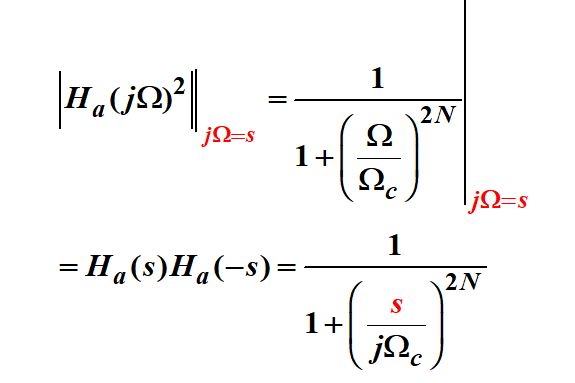
求極點,也就是令分母多項式為零,得到:
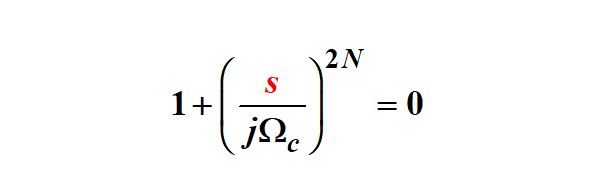
解上面的2N階方程,得到2N個根(極點):
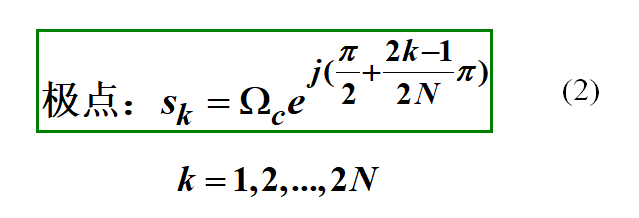
用公式表示,看上去似乎很復雜,我們以N=3為例,這6個極點分別為:
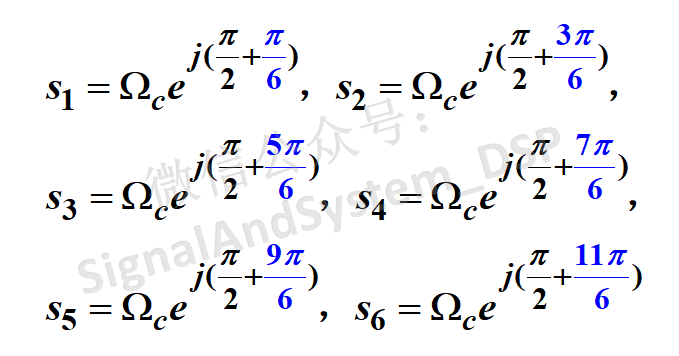
畫在圖上(零極點圖)就一目了然了:
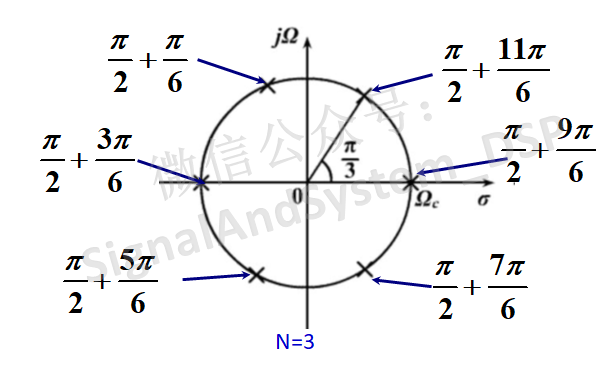
也就是說,Ha(s)Ha(-s)的 2N 個極點等間隔地分布在半徑為 Wc的圓上。
說到這里,我們開篇時的那個疑問 “ 為什么不直接作為幅度函數,而是幅度平方函數 ” ,也找到答案了。不能把它直接作為幅度函數,否則無法得到因果穩定系統。而作為幅度平方函數,我們只要取左半平面的N個極點構成Ha(s),就可以由幅度平方函數得到系統函數了。并且,根據極點,構造出的系統函數Ha(s),自然就是有理分式的形式。
看到這里,有的小伙伴會擔心地想 “ 如果極點在虛軸上,那可咋辦呢?”。其實,我們觀察一下極點sk的表達式就是發現,這個擔心是多余的,巴特沃斯函數的極點永遠不會落在虛軸上。
總結一下,N階巴特沃斯函數構成的濾波器的系統函數是:
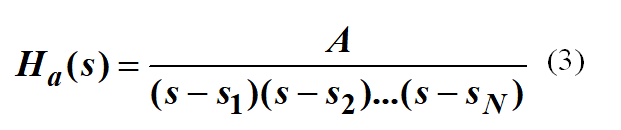
常數A怎么確定呢?
簡單,我們只要取一個特殊點(最簡單的當然是W=0,或者說s=0),分別代入到(1)式和(3)式中,就可以得到:
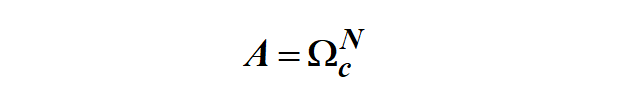
即:N階巴特沃斯函數構成的濾波器的系統函數是:
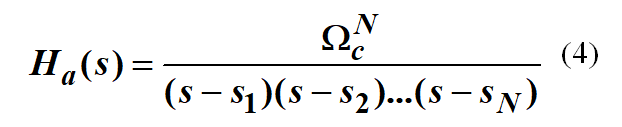
3. 巴特沃斯濾波器的階數
所謂的濾波器設計,就是得到系統函數,也就是上面的(4)式。可見,只要求出N和Wc,就萬事大吉了。
N和Wc怎么確定呢?當然是根據濾波器的性能指標來確定。
下面首先來看,階數N怎么求。
我們知道,N越大,通帶性能越平坦(即通帶衰減越小),而阻帶衰減越大,并且過渡帶越窄,即濾波器性能越好。這只是一個定性的分析,要定量的分析,還要從公式出發。
首先,我們來看一看濾波器的性能指標,看下圖:Wp、Ws分別為通帶截止頻率和阻帶截止頻率,Ap、As分別為通帶最大衰減和阻帶最小衰減(均以dB為單位)。而巴特沃斯函數是單調遞減的,所以,只要當W=Wp時,衰減不大于(即≤)Ap、W=Ws時,衰減不小于(即≥)As,那么在通帶內和阻帶內,肯定是滿足技術指標要求的。
注意 分清這三個W ,Wc是3dB截止頻率,即W=Wc時,幅度特性正好是-3dB,而一般來說,通帶最大衰減Ap要小于3dB,而阻帶最小衰減As一般為幾十dB以上,所以,一般來說,Wc要大于Wp而且遠遠小于Ws。
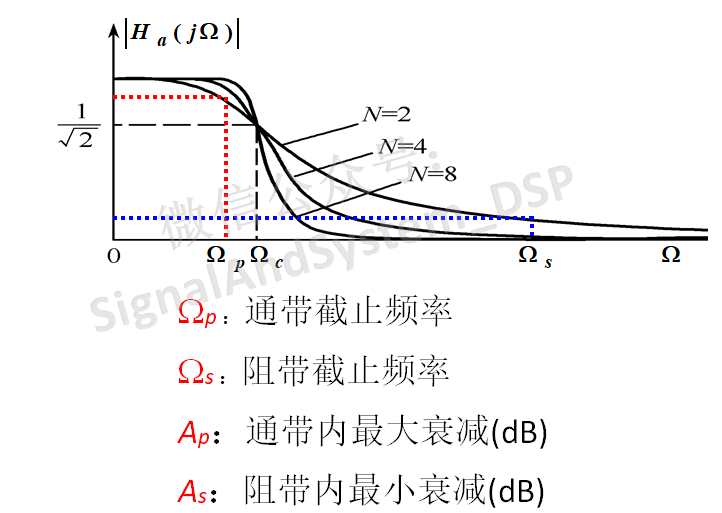
這樣,我們只要把 W=Wp 和 W=Ws 代入到巴特沃斯函數中,然后取10倍的log(轉換為dB),得到兩個不等式:
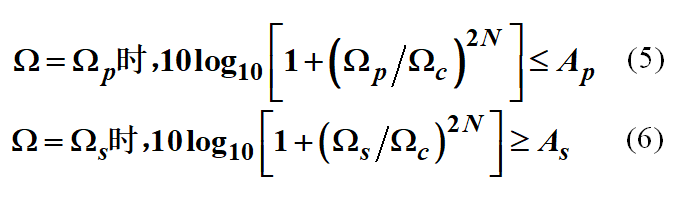
根據(5)和(6)可得:
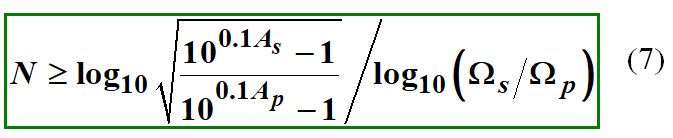
這樣,將表示技術指標的這四個值帶入上式中,就可以得到滿足該指標的濾波器階數N的條件,取滿足該條件的最小的整數(例如得到4.21,我們就得取N=5),就是我們需要的濾波器階數。
4. 巴特沃斯濾波器的3dB截止頻率
N確定了,巴特沃斯函數中還有一個參數:Wc 怎么得到呢?
將剛剛求出的N帶入到上圖的(5)式或者(6)式中(把≤和≥變為=),都可以得到 Wc。顯然,這兩個Wc是不同的。
如果用(5)式取 = 號得到的Wc,即
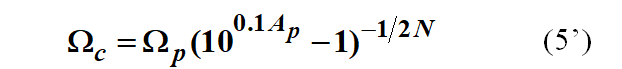
那么,通帶最大衰減剛剛好滿足指標要求,而阻帶最小衰減會略大于指標要求。這是因為,我們按照(7)式得到的往往不是整數,我們實際上取的N是大于臨界條件的最小整數。
阻帶衰減越大,說明濾除得更徹底,也就是說,如果根據(5)求出的Wc,我們的巴特沃斯濾波器的通帶性能剛剛好滿足指標要求,而阻帶性能會略高于要求(也可以稱之為有富裕)。
反之,如果用(6)式取 = 號得到的Wc,即
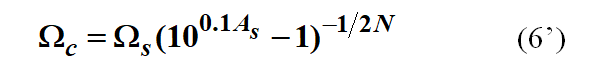
那么,阻帶最小衰減剛剛好滿足指標要求,而通帶最大衰減會略小指標要求。此時,通帶性能有富裕。
如果設計任務本身就是設計模擬濾波器,那么就可以根據實際需要,來決定用(5)式或者(6)式來確定Wc。如果沒有特殊要求,用哪個都行,都能得到滿足性能要求的濾波器。
正如我們前面所說,在實際使用中,“模擬濾波器”設計一般是數字濾波器設計的中間一步,可以根據模擬濾波器轉換為數字濾波器時采用的方法對濾波器幅頻特性的不同影響,來選擇那個式子求Wc。這一點,在下一篇中還會涉及到。
5. 巴特沃斯濾波器的設計
總結一下,根據前面所述,巴特沃斯濾波器設計可以按照下面的步驟:
第一步,根據濾波器性能指標,確定N和Wc;
第二步,根據N和Wc,求出幅度平方函數的2N個極點;
第三步,取左半平面的N個極點,構造出濾波器的系統函數Ha(s)。
上述步驟,從原理上講,是沒問題的。但實際上,還有更簡便的方法。我們的前輩工程師們是很聰明的,他們想到了,將Wc設為1(稱為 歸一化 ),針對N=2、3、4......,分別計算出對應的濾波器(稱為歸一化原型濾波器)的系統函數HaN(s)的系數,存成表格。
這樣,在具體應用場景中,只要計算出階數N,去查表,然后做一個神奇的操作—— 去歸一化 ,就可以得到所需要的濾波器的系統函數了。
這個神奇的操作——去歸一化,到底是怎么回事呢?看下圖:

下面解釋一下上圖的這個去歸一化是怎么回事。
我們把(4)式的分子分母同除以Wc,然后,令s/Wc等于 p (稱為歸一化復變量),得到一個新的函數,我們記為HaN(p),我們稱之為歸一化原型濾波器的系統函數,它的極點pk,稱為歸一化極點。
相反的過程,也就是根據HaN(p),令 p=s/Wc,重新得到關于s的函數Ha(s),稱 為去歸一化 。
把(8)式的分母展開,就得到:
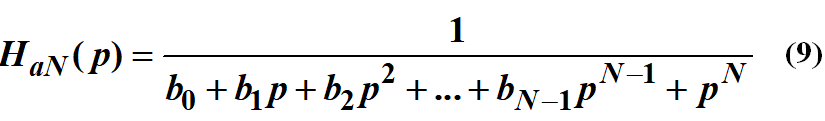
注意,常數項b0一定等于1,而且最高次項p^N的系數也一定是1。
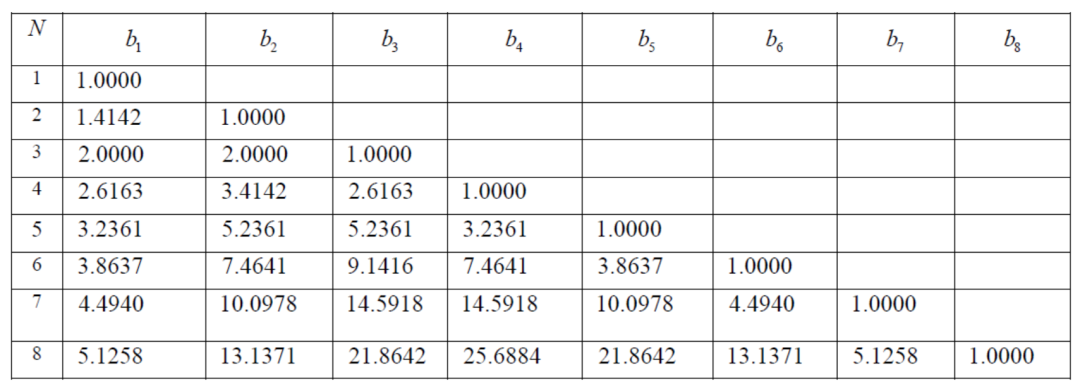
上式中的系數bi,前輩工程師們在上個世紀三十年代沒有計算機的幫助下用鉛筆和稿紙手工千辛萬苦計算而形成了表格。只要計算出了階數N,直接查表就可以了。
利用歸一化的思想,修正一下前面總結的設計步驟,如下:
第一步 ,根據濾波器性能指標,確定N;
第二步 ,根據N,查表得到歸一化濾波器的系數;
第三步 ,求出Wc,去歸一化,得到Ha(s)的系數。
講了這么多,還是要拿道題目來練練手吧。

【解】:
第一步,求N。
根據濾波器指標
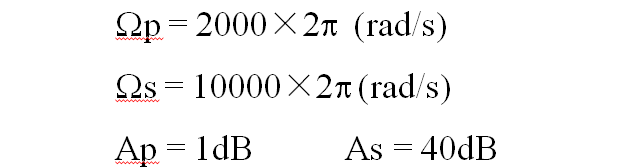
帶入(3)式得到:N≥3.28
所以,取N=4
第二步,查表,得到歸一化原型濾波器系統函數 HaN(p) 的系數b1、b2、b3如下所示;
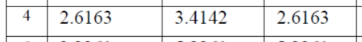
所以,歸一化原型濾波器的系統函數為
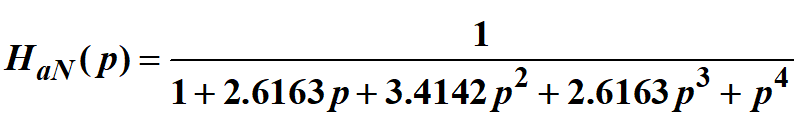
第三步,求Wc。
如果用(5‘)式求Wc,得到:
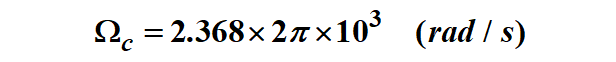
如果用(6‘)式求Wc,得到:
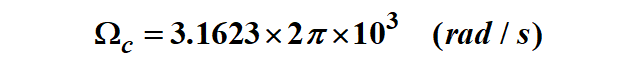
第四步,去歸一化
得到巴特沃斯濾波器的系統函數為

6. 巴特沃斯濾波器的特點
巴特沃斯函數函數的特點,決定了巴特沃斯濾波器的特點,也就是幅頻特性曲線是W的單調遞減函數,這樣的特點,是好?還是不好呢?
比如前面那道例題,我們設計得到的4階巴特沃斯濾波器,在2kHz處衰減為1dB,那么在頻率小于2kHz處,衰減會小于1dB。同樣的,在頻率大于10kHz處,衰減會大于40dB,當然這沒有問題,因為畢竟通帶內衰減越小越好,而阻帶內衰減越大越好。
但是,從實現的角度來看,這一特點并不 “劃算”,或者說,不經濟,比較費錢。因為階數越高,對系統硬件性能要求越高,成本越高。我們寧愿,通帶和阻帶內的特性均勻分布。也就是說,更經濟的方法是,不是采用單調遞減特性的巴特沃斯函數,而是采用其他具有某種起伏特性的函數,只要能夠控制其起伏的范圍就可以。
這就是下面要說的切比雪夫濾波器和橢圓濾波器。
三 切比雪夫濾波器
相比于名不見經傳的巴特沃斯,切比雪夫可以說是大名鼎鼎,他是一位著名的俄國數學家。我們用到的,就是以他的名字命名的一種多項式——切比雪夫多項式:
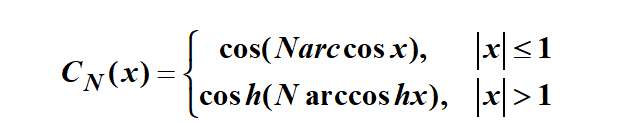
這個多項式的特點是:當 |x|≤1時,CN(x)是余弦函數,具有等波紋幅度特性;當|x|>1時,是雙曲余弦函數,隨x單調增加。
下圖中這些五顏六色的線條,分別是N=0(藍)、N=1(綠)、N=2(紅)、N=3(黑)、N=4(黑)、N=5(紫)時的切比雪夫多項式CN(x) 曲線。可見,在 |x| < 1 范圍內,都具有等波紋,N的數目決定了波動的次數;在 |x| > 1范圍內,具有單調遞增或遞減的特點,并且N越大,遞增或遞減的速度越快。
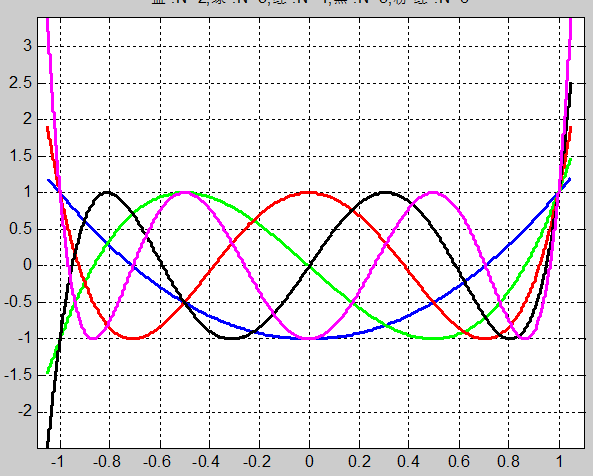
這樣,我們就可以利用它的等波紋特點,構造濾波器的通帶或阻帶,而利用它的單調特性,構造過渡帶。從而有兩種類型的切比雪夫濾波器:

上面公式中,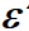 的取值范圍為 0~1,表示波紋大小,其值越大,波紋越大;Wc為截止頻率;CN為切比雪夫多項式,N為階數。
的取值范圍為 0~1,表示波紋大小,其值越大,波紋越大;Wc為截止頻率;CN為切比雪夫多項式,N為階數。
這兩種濾波器的幅度特性分別如下圖所示:
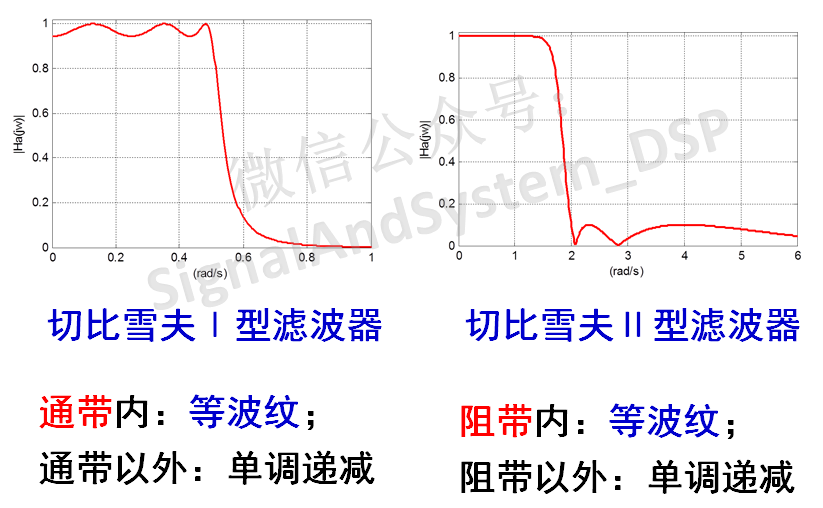
切比雪夫濾波器的設計方法,與巴特沃斯濾波器類似,也是根據濾波器技術指標,計算出N和Wc,查表得到歸一化原型濾波器的系數,再去歸一化,得到所需濾波器的系統函數系數。只是其計算過程更為繁瑣。這里不再贅述。
四 橢圓濾波器
上面所說的兩種類型的切比雪夫濾波器,分別實現了通帶或者阻帶內等波紋,而采用雅可比橢圓函數構造幅度平方函數的橢圓濾波器,在通帶和阻帶內都具有等波紋的特性。
下圖為橢圓濾波器的幅度函數曲線。因為1931年考爾(Cauer)首先對這種濾波器進行了理論證明,故又稱為考爾濾波器。
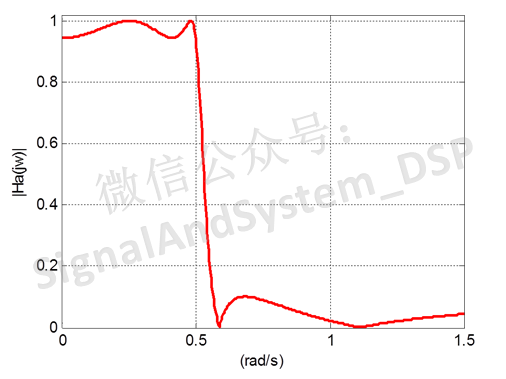
因其表達式較為復雜,此處不再贅述。
五 幾種模擬濾波器的比較
上面介紹了幾種常用的模擬濾波器,下面表格對這幾種濾波器的幅度特性做了比較。
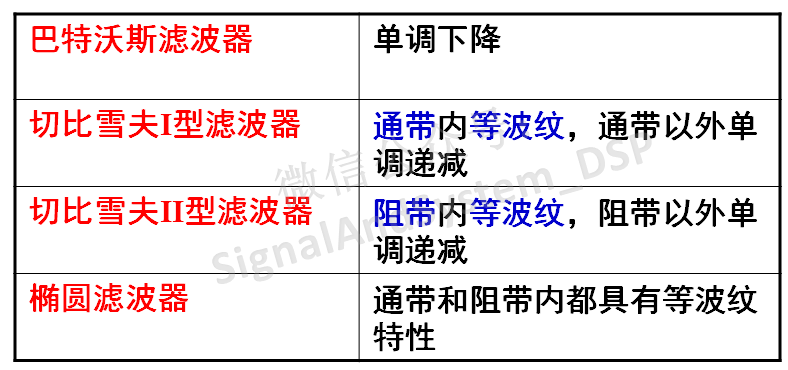
在滿足相同的濾波器幅頻響應指標條件下,巴特沃斯濾波器階數最高,而橢圓濾波器階數最低。
matlab中的信號處理工具箱中,提供了豐富的濾波器設計的函數。下表中給出了與本文這幾種濾波器有關的函數。
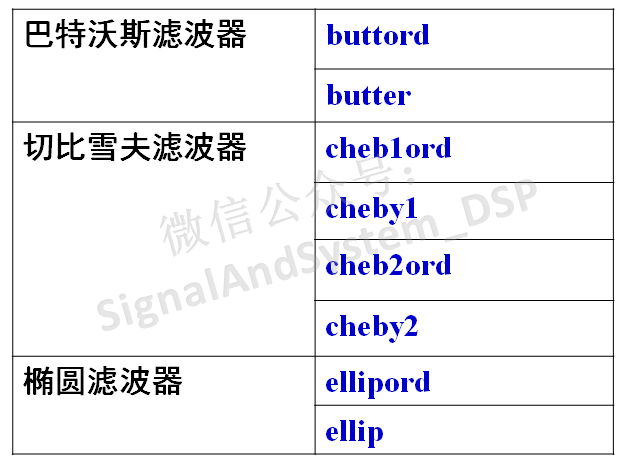
具體函數的使用方法,這里不再贅述,可以在matlab的幫助中查看。
本文的最后,結合一道例題,給出其matlab程序和仿真結果。

matlab仿真程序如下:
% 設計巴特沃斯模擬濾波器
%濾波器指標:通帶截止頻率:2000πrad/s,阻帶截止頻率:4000πrad/s,
%通帶最大衰減:1dB,阻帶最小衰減:40dB
%編寫者:丹梅
close all;clear;clc;
%濾波器的性能指標
wp = 10002pi;%通帶截止頻率,單位:rad/s
ws = 20002pi;%阻帶截止頻率,單位:rad/s
Rp = 1;%通帶最大衰減,單位:dB
Rs = 40;%阻帶最小衰減,單位:dB
%----------------巴特沃斯濾波器--------------------%
% 計算滿足性能指標的濾波器階數n和3dB截止頻率wn
[n_BW,wn_BW] = buttord(wp,ws,Rp,Rs,'s');
% 計算模擬低通濾波器的傳輸函數Ha(s)(傳輸函數為分子、分母多項式形式)
[b_BW,a_BW] = butter(n_BW,wn_BW,'s');
%----------------切比雪夫1型濾波器--------------------%
% 計算滿足性能指標的濾波器階數n和3dB截止頻率wn
[n_CB1,wn_CB1] = cheb1ord(wp,ws,Rp,Rs,'s');
%注意:與buttord函數不同,cheb1ord函數返回參數的第二個wn就是wp,而不是3dB截止頻率
% 計算模擬低通濾波器的傳輸函數Ha(s)(傳輸函數為分子、分母多項式形式)
[b_CB1,a_CB1] = cheby1(n_CB1,Rp,wn_CB1,'s');
%----------------切比雪夫2型濾波器--------------------%
% 計算滿足性能指標的濾波器階數n和3dB截止頻率wn
[n_CB2,wn_CB2] = cheb2ord(wp,ws,Rp,Rs,'s');
%注意:與buttord函數不同,cheb1ord函數返回參數的第二個wn就是wp,而不是3dB截止頻率
% 計算模擬低通濾波器的傳輸函數Ha(s)(傳輸函數為分子、分母多項式形式)
[b_CB2,a_CB2] = cheby2(n_CB2,Rs,wn_CB2,'s');
%----------------橢圓(考爾)濾波器--------------------%
% 計算滿足性能指標的濾波器階數n和3dB截止頻率wn
[n_EL,wn_EL]=ellipord(wp,ws,Rp,Rs,'s');
% 計算模擬低通濾波器的傳輸函數Ha(s)(傳輸函數為分子、分母多項式形式)
[b_EL,a_EL]=ellip(n_EL,Rp,Rs,wn_EL,'s');
%---------------輸出四種濾波器階數-------------------%
display('巴特沃斯濾波器階數:');n_BW
display('切比雪夫1型濾波器階數:');n_CB1
display('切比雪夫2型濾波器階數:');n_CB2
display('橢圓濾波器階數:');n_EL
%---------------輸出濾波器頻率響應-------------------%
% 求模擬濾波器的頻率響應(分析頻率范圍為w = 0~2*ws)
w = [0:1:500]2ws/500;
H_BW = freqs(b_BW,a_BW,w);
db_BW = 20*log10((abs(H_BW)+eps)/max(abs(H_BW)));
H_CB1 = freqs(b_CB1,a_CB1,w);
db_CB1 = 20*log10((abs(H_CB1)+eps)/max(abs(H_CB1)));
H_CB2 = freqs(b_CB2,a_CB2,w);
db_CB2 = 20*log10((abs(H_CB2)+eps)/max(abs(H_CB2)));
H_EL = freqs(b_EL,a_EL,w);
db_EL = 20*log10((abs(H_EL)+eps)/max(abs(H_EL)));
% 繪圖(為了讀數方便,橫坐標對pi進行了歸一化)
figure;
subplot(221);plot(w/pi,db_BW,'LineWidth',2);
xlabel('(rad/s)');ylabel('(dB)');title('巴特沃斯濾波器');grid on;
subplot(222);plot(w/pi,db_CB1,'LineWidth',2);
xlabel('(rad/s)');ylabel('(dB)');title('切比雪夫1型濾波器');grid on;
subplot(223);plot(w/pi,db_CB2,'LineWidth',2);
xlabel('(rad/s)');ylabel('(dB)');title('切比雪夫2型濾波器');grid on;
subplot(224);plot(w/pi,db_EL,'LineWidth',2);
xlabel('(rad/s)');ylabel('(dB)');title('橢圓濾波器');grid on;
運行結果如下:

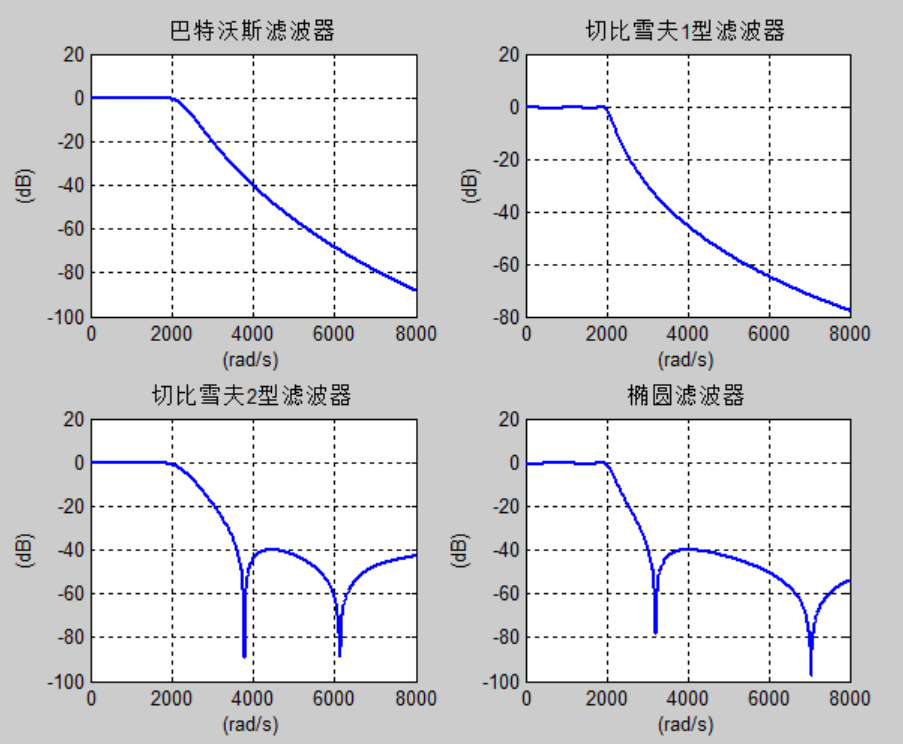
-
低通濾波器
+關注
關注
13文章
470瀏覽量
47209 -
模擬濾波器
+關注
關注
0文章
30瀏覽量
13383 -
AD轉換器
+關注
關注
4文章
249瀏覽量
41289 -
MATLAB仿真
+關注
關注
4文章
175瀏覽量
19841 -
數字信號處理器
+關注
關注
5文章
428瀏覽量
27282
發布評論請先 登錄
相關推薦
一種八腔帶通腔體濾波器的設計方法
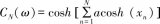




 分享一種模擬濾波器設計方法
分享一種模擬濾波器設計方法










評論