誤差矢量幅度(EVM)是廣為使用的系統級性能指標,許多通信標準將其定義為用于無線局域網(WLAN 802.11)、移動通信(4G LTE、5G)等應用的合規性測試。除此之外,它還是一個極為有用的系統級指標,可通過簡單易懂的值來量化系統中所有潛在損害的綜合影響。
大多數射頻工程師都會接受有關大量射頻性能參數的培訓,例如噪聲系數、三階截取點和信噪比。了解這些性能參數對整體系統級性能的綜合影響可能極具挑戰性。EVM不評估多個單獨的性能指標,而是反映整個系統的概況。在本文中,ADI將分析較低水平的性能參數如何影響EVM,并研究一些將EVM用于器件系統級性能優化的實際示例。同時展示如何實現比大多數通信標準目標低15dB之多的EVM。
什么是誤差矢量幅度?
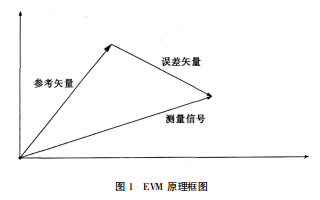
EVM是量化系統中所有信號綜合損害的簡單指標。采用數字調制的器件經常定義這個指標,可通過同相(I)和正交(Q)矢量圖(也稱為星座圖)來表示(如圖1a所示)。一般來說,計算EVM的方式是針對每個接收信號找到理想星座位置(如圖1b所示)。通過計算接收信號的位置與其最接近的理想星座位置之間的所有誤差矢量幅度的均方根(rms),可得出器件的EVM值。
符合IEEE 802.11標準的EVM公式示例見方程式1。
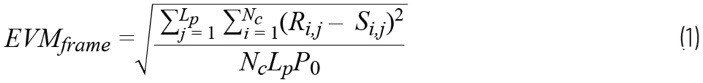
其中:Lp為幀數,Nc為載波數,Ri,j為接收信號,Si,j為理想信號位置。
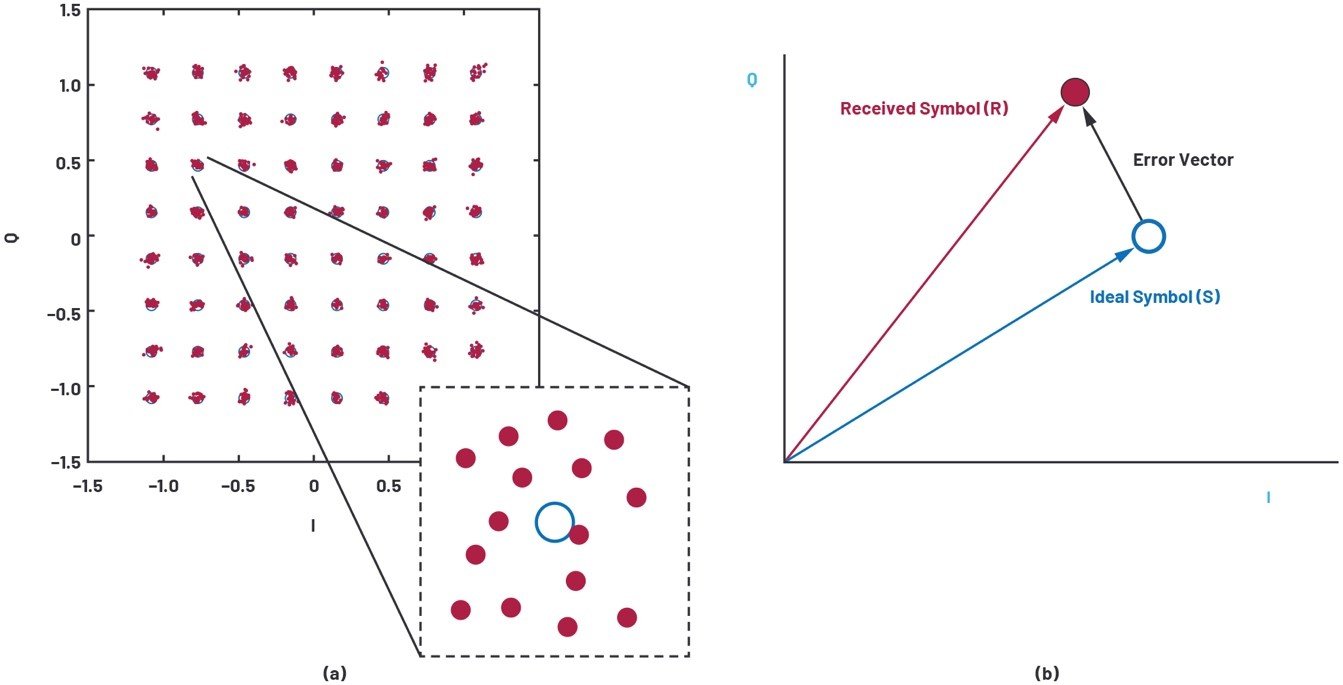
圖1.(a)星座圖和判定邊界,以及(b)接收信號和理想信號位置之間的誤差矢量。
EVM與給定系統的誤碼率(BER)密切相關。當接收信號遠離目標星座點時,它們落入另一星座點判定邊界內的概率會隨之而增加。這會使BER變大。BER和EVM之間的一個重要區別是,發射信號的BER是根據發射的位模式計算的,而EVM則根據離信號最近的星座點和信號實際位置的距離計算的。在某些情況下,信號可能會跨越判定邊界,并被賦予不正確的位模式。如果信號越靠近另一理想信號位置,則該信號的EVM可能會越好。因此,雖然EVM和BER密切相關,但這種關系可能不適用于信號失真水平極高的情況。
現代通信標準根據發射或接收信號的特征(如數據速率和帶寬)規定了最低可接受的EVM水平。達到目標EVM水平的器件符合標準,而未達到目標EVM水平的器件則不符合標準。專門用于通信標準合規性驗證的測試和測量設備通常會采用更嚴格的EVM指標,該指標可能會比標準制定的EVM指標低一個數量級。這使得測試和測量設備能在不使信號明顯失真的情況下表征受測器件的EVM特性。
影響EVM的因素有哪些?
作為一種誤差指標,EVM與系統內的所有誤差源密切相關。為了量化所有損害對EVM的影響,可以計算它們使接收和發射信號失真的程度。下面ADI將分析幾個關鍵損害(如熱噪聲、相位噪聲和非線性)對EVM的影響。
白噪聲
白噪聲存在于所有射頻系統中。當噪聲是系統中唯一的損害時,可使用以下公式計算出相應的EVM:

其中SNR是系統的信噪比(單位:dB),PAPR是給定信號的峰均功率比(單位:dB)。請注意,SNR一般適用于單音信號。如果是調制信號,則需考慮信號的PAPR。由于單音信號的PAPR為3dB,如果波形具有任意PAPR值,則需從SNR值中減去3dB。
對于高速轉換器(如模數轉換器(ADC)和數模轉換器(DAC)),方程式2可用噪聲頻譜密度(NSD)表示:
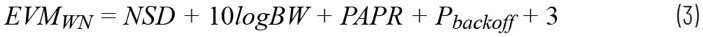
其中,NSD為噪聲頻譜密度(單位:dBFS/Hz),BW為信號帶寬(單位:Hz),PAPR為峰均功率比,Pbackoff為信號峰值功率與轉換器滿量程之間的差值。通過該公式,可非常方便地使用NSD規范直接計算器件的預期EVM,該規范通常用于最先進的高速轉換器。請注意,高速轉換器器件也需考慮量化噪聲。大多數高速轉換器的NSD規范也涵蓋量化噪聲。因此,方程式3不僅代表熱噪聲,還代表高速轉換器的量化噪聲。
正如這兩個方程式所強調的,信號的EVM與其總信號帶寬、峰均比和整個系統的熱噪聲直接相關。
相位噪聲如何影響EVM
相位噪聲是影響系統EVM的另一種形式的噪聲,是波形相位和頻率的隨機波動。所有非線性電路元件均會引入相位噪聲。給定系統的主要相位噪聲來源可以追溯到振蕩器,如參考時鐘、本振(LO)和采樣時鐘。多個振蕩器(如數據轉換器的采樣時鐘、用于頻率轉換的本振以及基準頻率)會對系統的總體相位噪聲產生影響。
相位噪聲導致的性能下降與頻率有關。典型振蕩器在其基本振蕩頻率(所謂的中心頻率)下產生出大部分載波能量。一小部分的信號能量將在這個中心頻率附近傳播。特定頻率偏移下1 Hz帶寬內的信號幅度與其在中心頻率下的幅度之比定義即為特定頻率偏移下的相位噪聲(如圖2所示)。
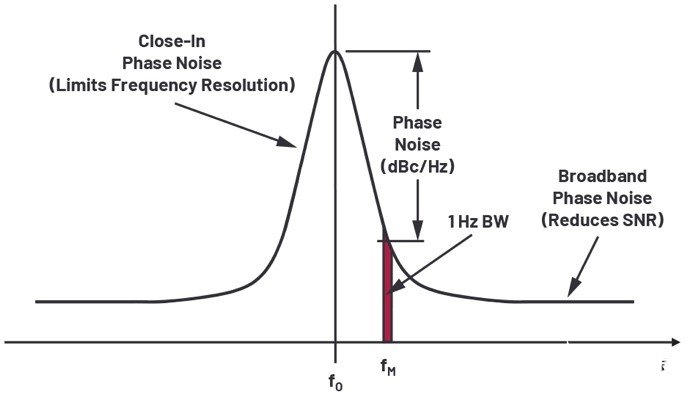
圖2.相位噪聲
系統的相位噪聲會直接影響系統的EVM。在整個帶寬內對相位噪聲求積分,可計算出系統相位噪聲引起的EVM。對于大多數采用正交頻域調制(OFDM)的現代通信標準,應從大約10%的副載波間隔開始對相位噪聲求積分,直至達到總信號帶寬時結束。

其中,L為單邊帶相位噪聲密度,fsc為副載波間隔,BW為信號帶寬。
大多數頻率發生器件在低于2GHz的頻率下出現低相位噪聲,典型的積分抖動水平比標準中定義的EVM限值低幾個數量級。但在更高的頻率和更寬的信號帶寬下,積分相位噪聲水平可能會非常大,這可能導致EVM值顯著變高。工作頻率大于20GHz的毫米波(mmWave)器件通常會發生這種情況。要獲得最佳的整體EVM,應計算整個系統的相位噪聲,這將在“設計示例”部分詳細討論。
計算非線性對EVM的影響
系統級非線性會導致可能處于信號帶寬范圍內的交調產物。這些交調產物可與副載波重疊,影響它們的幅度和相位。可計算出源自這些交調項的平均誤差。讓我們推導一個簡單的公式來計算三階交調產物引起的系統EVM。
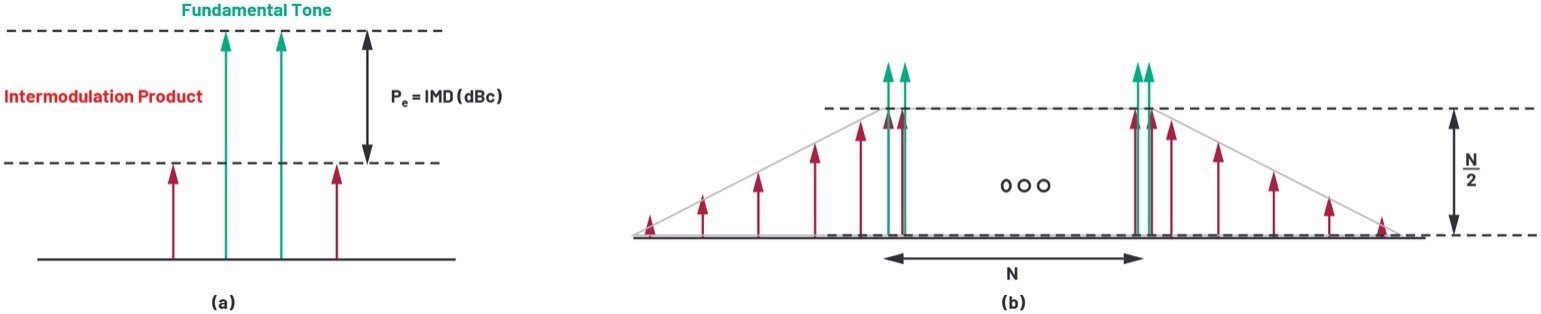
圖3.OFDM交調產物
如圖3a所示,雙音信號將產生兩個交調產物。交調產物的功率可通過下式計算:


其中,Ptone為測試音的功率,OIP3為輸出三階截取點,Pe為誤差信號,表示基波和交調產物之間的功率差。
如果OFDM信號具有N個信號音(如圖3b所示),則方程式6變為:
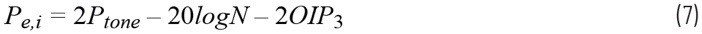
由于在每個副載波位置有N/2個交調產物重疊,因此可將方程式改寫為:
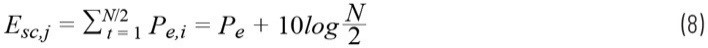
包括所有副載波位置在內的總誤差為:
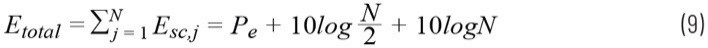
將方程式6代入方程式8,EVM可表示如下:
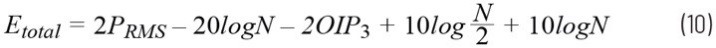
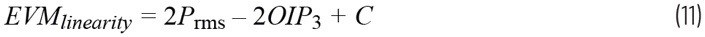
其中,PRMS為信號的均方根平均值,而C為一個常數(范圍介于0dB至3dB之間,具體取決于調制方案)。如方程式11所示,EVM隨著系統的OIP3的升高而降低。這與預期相符,因為OIP3越高,通常意味著系統更具線性。此外,隨著信號均方根功率的降低,EVM隨著非線性產物功率的降低而降低。
使用EVM優化系統級性能
典型系統級設計均始于級聯分析,使用構建模塊的低級別性能參數來確定使用這些模塊構建而成的系統的整體性能。可用于計算這些參數的分析公式和工具均已非常完善。但許多工程師并未考慮如何正確使用級聯分析工具來設計出經過充分優化的系統。
作為系統級性能指標,EVM為設計工程師優化系統設計提供了重要的參考。設計人員可以無需考慮多個參數,而只需輕松選擇優化EVM均方根值,便能實現最佳系統設計。
EVM浴盆曲線
下面可以從每個損害產生的EVM影響和輸出功率電平考慮,將這些因素合并成單張圖。圖4顯示了基于工作功率水平的系統典型EVM浴盆曲線。在低工作功率水平下,EVM性能主要由系統的噪聲性能決定。在高工作功率水平下,系統的非線性會影響EVM。系統的最低EVM水平通常根據所有誤差源(包括相位噪聲)的組合來定義。
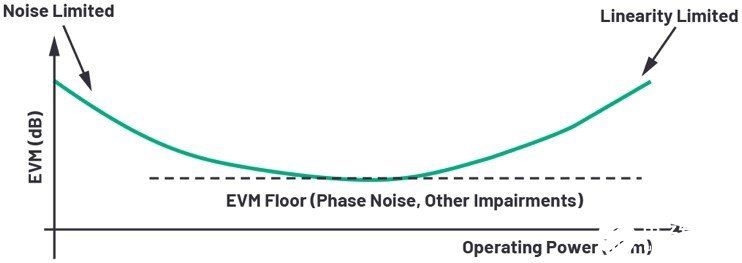
圖4.EVM浴盆曲線,顯示EVM隨工作功率的變化
可通過方程式12歸納總EVM:
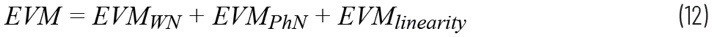
其中EVMWN為源自白噪聲的EVM影響,EVMPhN為相位噪聲影響,EVMlinearity為源自非線性失真的EVM。對于給定的功率水平,所有這些誤差項的功率和表示了系統中的總EVM水平。
除方程式12外,系統的浴盆曲線在系統級優化中也非常有用,能夠以組合的形式直觀呈現出給定系統的所有損害。
設計示例
用EVM作為指標來設計一個實用的信號鏈。在本例中,ADI將使用RF采樣DAC、毫米波調制器、毫米波頻率產生器件和其他信號調理器件來設計一個毫米波發射器(如圖5所示)。
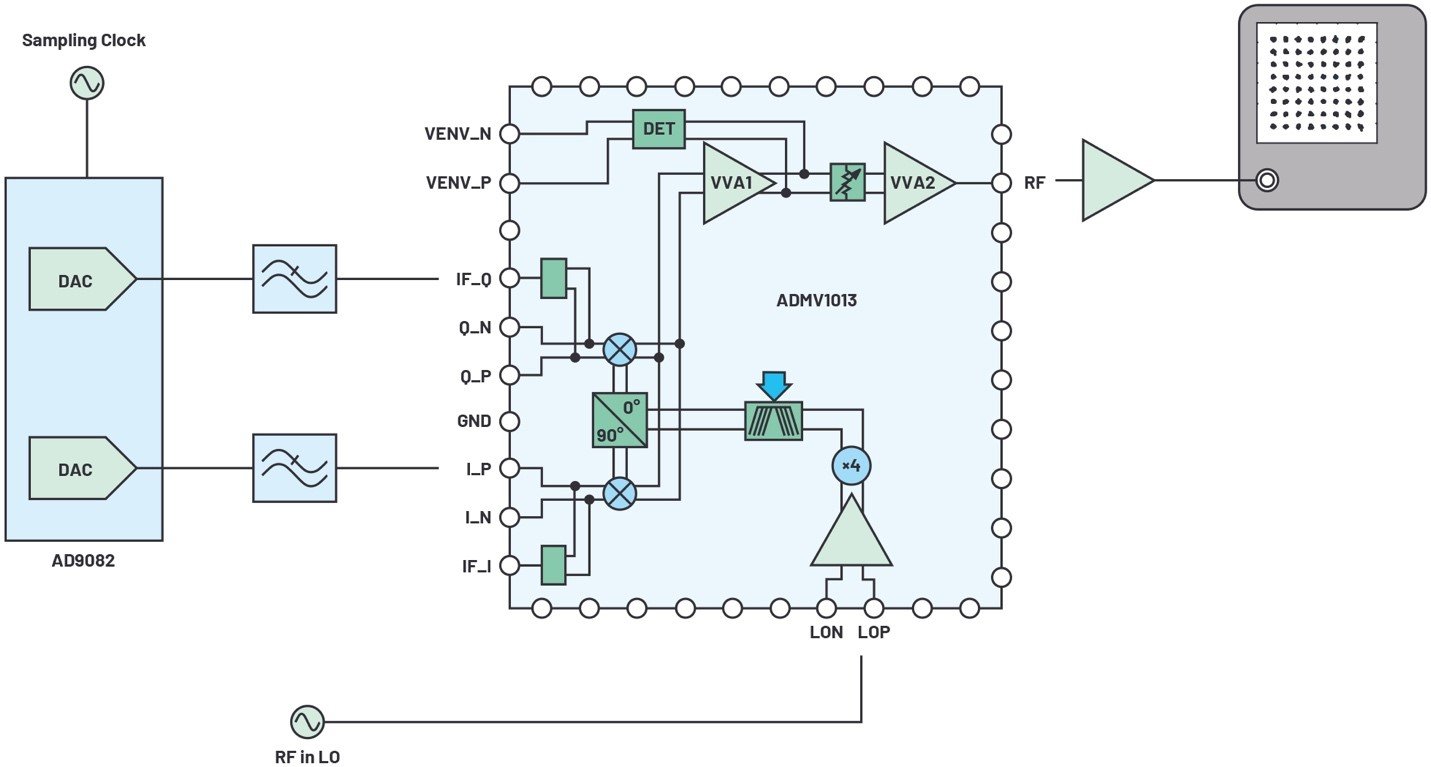
圖5. 毫米波發射器信號鏈
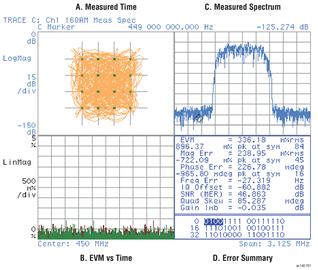
該信號鏈使用AD9082器件,該器件配備了采樣速率分別為12GSPS和6GSPS的四通道DAC和雙通道ADC。使用這些具有直接RF功能的轉換器可使毫米波信號鏈的設計更具靈活性,性能無與倫比。圖6顯示了使用12位10GSPS模數轉換器AD9213完成的AD9082的EVM測量值。這兩個器件采用環回配置,產生的EVM水平低至-62dB,比標準限值低27dB。
該信號鏈還使用完全集成的毫米波調制器(ADMV1013),該調制器將傳統信號鏈的多個子模塊(如倍頻器、正交混頻器和放大器)集成到一個元件中。為了降低濾波復雜度,我們在該設計中使用了復數IF拓撲,從而向調制器的正交混頻器饋入正交信號。這消除了上變頻信號的一個邊帶,與雙邊帶上變頻操作相比,降低了濾波復雜度。
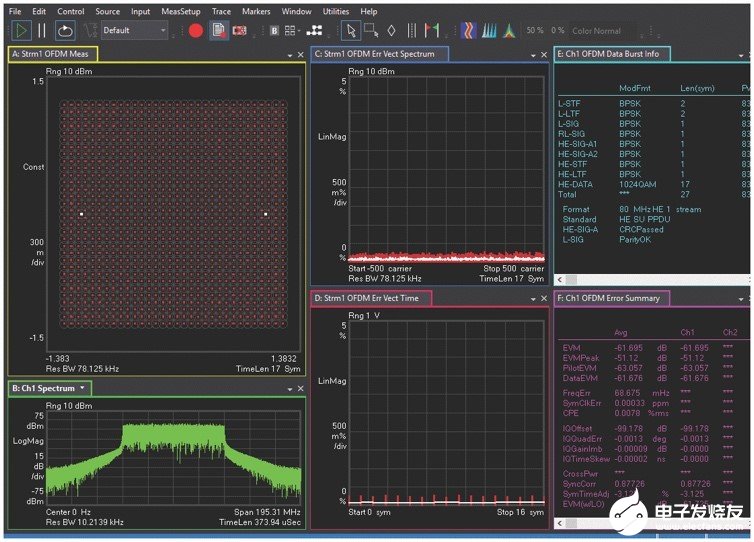
圖6.使用AD9213的AD9082在400MHz中頻下的典型EVM測量值(適用于80MHz帶寬IEEE 802.11ax波形,采用1024 QAM調制)。
為了優化該信號鏈以獲得最低EVM,可先分析系統級相位噪聲,然后討論噪聲和線性度之間的權衡,最后整合所有構建模塊。
通過最佳相位噪聲預算改善EVM
如前所述,整個系統的相位噪聲會限制毫米波頻率下的整體EVM性能。為了確保將整體EVM降至最低,先分析每一級的相位噪聲影響,以確保為該信號鏈挑選出最佳元件。
在該信號鏈中產生頻率的元件是DAC(使用合成器提供時鐘)和LO信號。總相位噪聲可表示為:

其中,LTx為發射器的總相位噪聲,?IF為DAC輸出端的相位噪聲,?LO為LO信號的相位噪聲。
本例中使用的DAC (AD9082)具有極低的附加相位噪聲。輸出端的總相位噪聲(即IF信號)可使用方程式14所示的簡單公式計算:
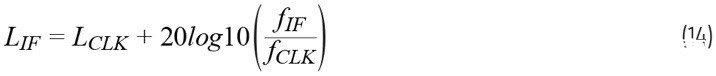
其中,LCLK為時鐘信號的積分相位噪聲,fIF為DAC輸出端的IF頻率,fCLK為DAC的采樣時鐘。下面分析采樣時鐘和LO源的兩個候選項,以確保挑選出相位噪聲和復雜度最低的元件。
圖7顯示了該信號鏈兩個主要頻率合成器候選項的單邊帶相位噪聲。使用6kHz至100MHz積分帶寬對信號源的相位噪聲求積分,可計算出5G NR波形的積分相位噪聲(如表1所示)。
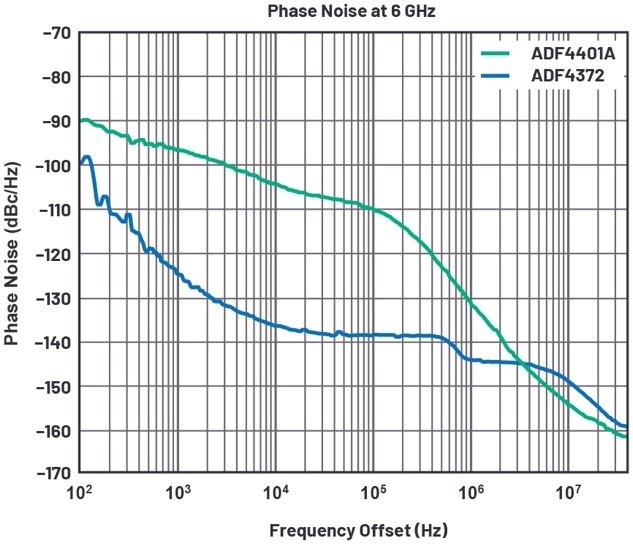
圖7.時鐘和LO源選項的相位噪聲
表1.合成器的典型積分相位噪聲測量值
| 元件 | 6GHz時的積分相位噪聲(dBc/Hz) | 2GHz時的積分相位噪聲(dBc/Hz) | 30GHz時的積分相位噪聲(dBc/Hz) |
| ADF4372 | -54.6 | -64.1 | -40.6 |
| ADF4401A | -73.1 | -82.6 | -59.1 |
在該信號鏈的典型中頻下,ADF4372和ADF4401A的積分噪聲水平都極低。由于ADF4372所需的總印刷電路板(PCB)面積小很多,因此是為產生IF信號的RF轉換器提供采樣時鐘的理想選擇。但正如所料,ADF4401A器件固有的起始相位噪聲較低,因此可選擇作為信號發生器來產生LO信號。在30GHz時,其積分噪聲比ADF4372器件低大約20dB。這種低積分相位噪聲水平確保了LO信號的相位噪聲不會限制整個系統的整體EVM性能。
利用方程式4,可按方程式15所示計算出由相位噪聲引起的總EVMPhN:
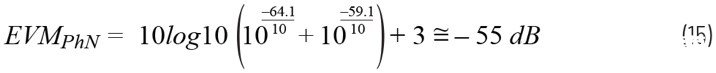
相位噪聲引起的這一EVM水平完全足以測量5G NR標準定義的信號(EVM水平約為-30dB)。
噪聲和線性度之間的權衡
RF設計中最基本的權衡之一就是在整個系統的噪聲性能和線性性能之間作出選擇。針對這兩個性能參數的其中一個進行優化通常會折損另一個參數的性能。當需要優化整個系統的性能時,系統級EVM分析是非常有用的工具。
圖8顯示了針對之前構建的信號鏈在噪聲和線性度之間作出的權衡。通過改變集成電壓可變放大器(VVA)控制電壓,得到了每條跡線。對于每條跡線,DAC的輸出功率電平均已改變。請注意,EVM隨著功率水平的升高而降低,原因是系統整體信噪比提高了。在某個功率電平之后,總信號路徑的非線性開始導致EVM性能降低。針對給定VVA配置產生的EVM浴盆曲線非常窄。
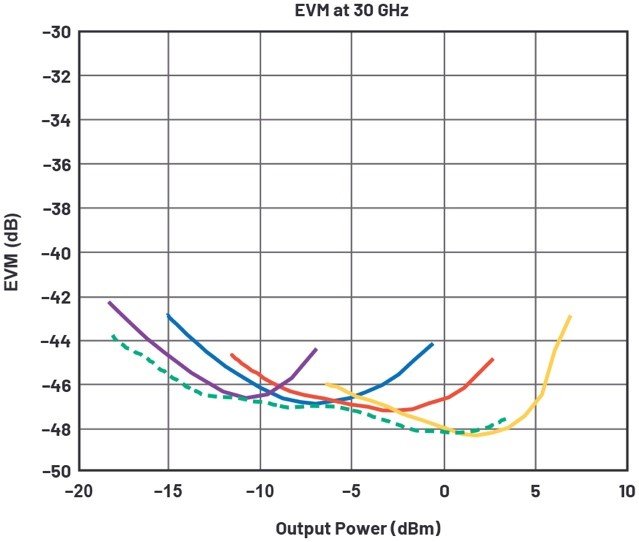
圖8.整個系統的噪聲和線性度之間的權衡
幸運的是,通過調整VVA控制電壓,可以過渡到另一條曲線,在這里整個系統的EVM較低。圖8中的虛線表示使用ADMV1013的集成VVA可實現的系統級優化。優化后產生的浴盆曲線顯著變寬,因此可在寬輸出功率水平范圍內實現超低EVM。
結論
在本文中,ADI討論了作為系統級性能指標的EVM,以及如何通過EVM優化系統級性能。正如文中所述,EVM是許多系統級問題的良好指標,可測量的EVM是所有誤差源的結果,可用于優化整體性能。同時已證明,使用最新的高速轉換器和完全集成的毫米波調制器,可展示出儀器儀表級性能,還可以實現與目標通信標準相比低幾個數量級的EVM。
-
ADI
+關注
關注
144文章
45812瀏覽量
248697 -
高速轉換器
+關注
關注
0文章
27瀏覽量
11807 -
EVM
+關注
關注
3文章
638瀏覽量
40989
發布評論請先 登錄
相關推薦
用于相鄰信道功率比和誤差矢量幅度測量的完整數字至射頻發送器包括包括原理圖和物料清單
矢量網絡分析儀E8362B的誤差來源及其校準-Agitkservice
矢量網絡分析儀的誤差來源于哪里?
寬帶低誤差矢量幅度(EVM)直接變頻發射機

是德科技推出可實現實現極低的剩余誤差矢量幅度的矢量網絡分析儀
誤差矢量幅度測量如何提高系統級性能
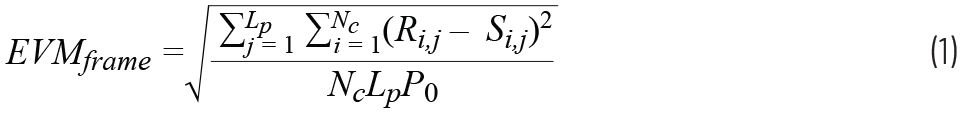




 誤差矢量幅度(EVM)測量怎樣提高系統級性能
誤差矢量幅度(EVM)測量怎樣提高系統級性能

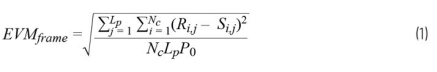











評論