1.概述:
應用矢量控制時其坐標變換是基礎,相關文獻與資料都有很多,matlab還有自帶模塊,但是一般都直接就給個變換矩陣讓人晦澀難懂。本文分享學習理解與推導過程。
2.Clarke變換分析推導過程
引用空間概念可得:

根據分析建模:
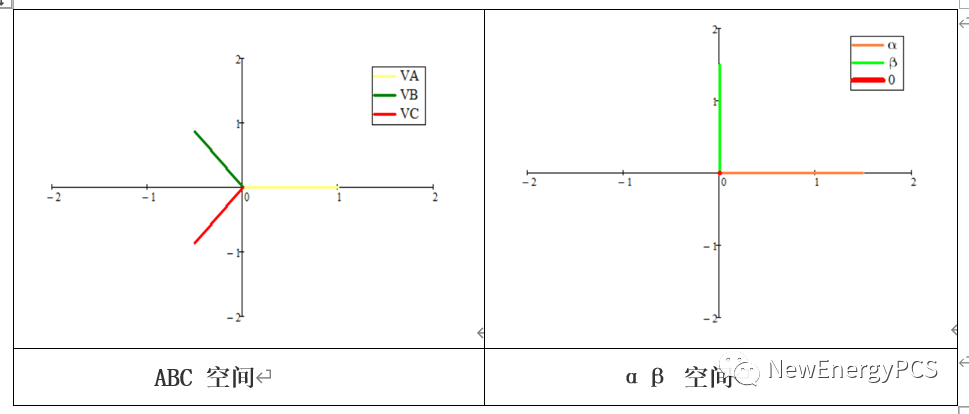
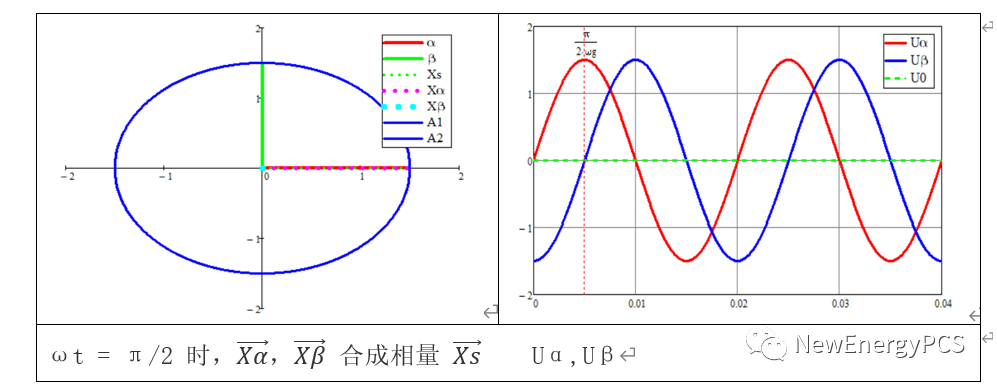
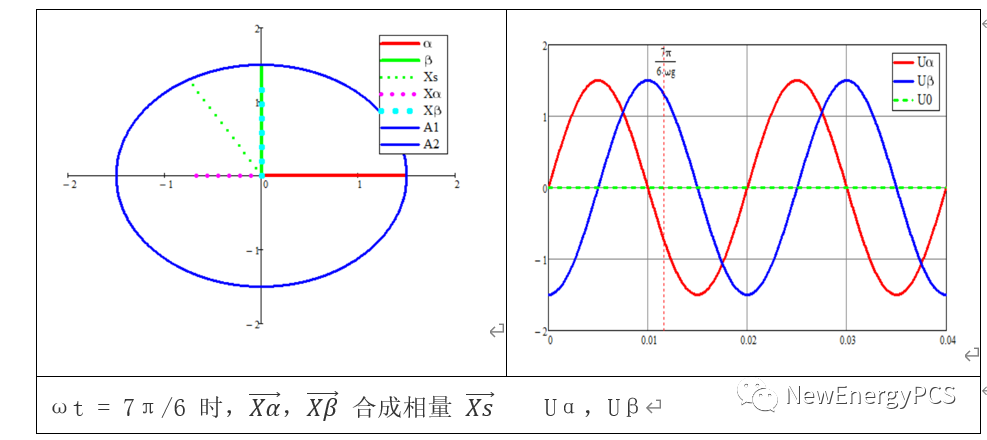
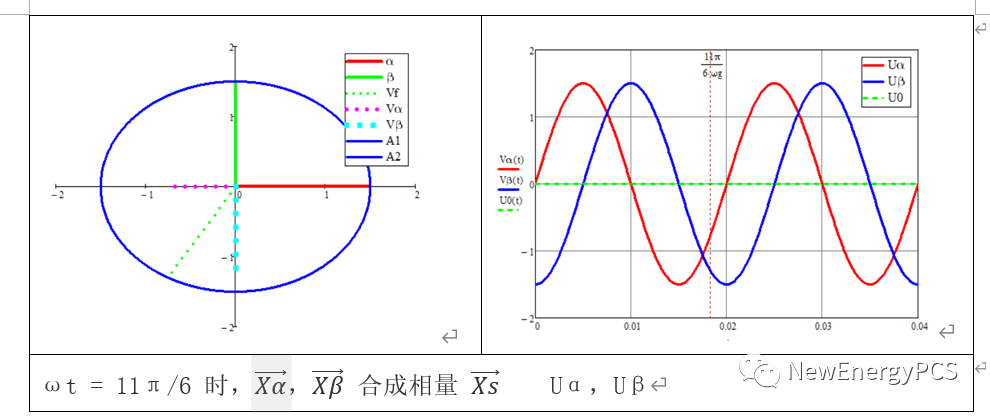
可得結論:
abc 系統轉換為αβ系統的變換就是Clarke變換。在上面的分析中旋轉矢量的長度相等,得到Uα,Uβ的幅值是3/2,通過調整Clarke變換中的系數,可以調整abc 系統與αβ系統中的幅值大小相等,功率相等,有效值相等。被稱為恒幅值變換,恒功率變換,恒有效值變換。

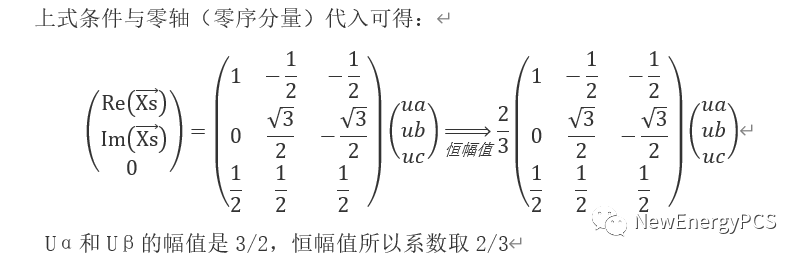


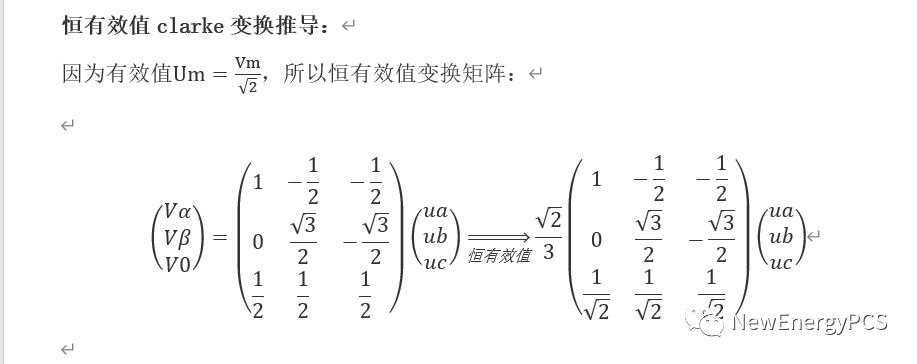
通過上式使用mathcad搭建ABC三相靜止坐標與αβ 0兩相靜止坐標。三相對稱時零軸分量為0 。
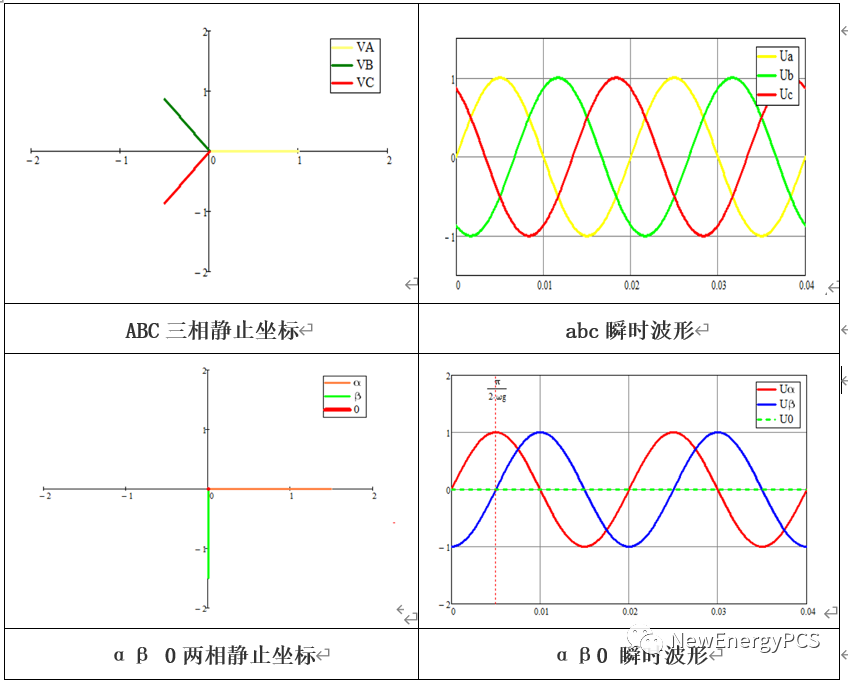
注意上圖使用sin正弦量用正序A B C作 3S/2S變換,發現波形上Uα超前Uβ 90°。與我們定義的αβ 0兩相靜止坐標,β軸超前α 90°相反。這里有兩種方法修改模型,其一是我們修改sin正弦量把原來的正序改為負序A C B。
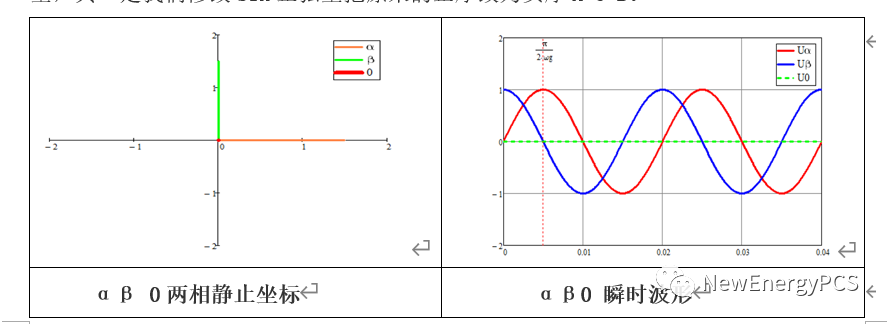
通過修改相序后需要修改clarke變換矩陣第二行的元素反號,即更改為了習慣的逆時針旋轉。
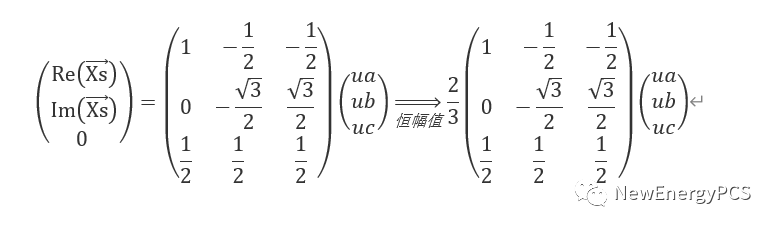
在這里聲明參考MATLAB官網的參考文檔,就暫時不修改相序,但也默認β軸超前α90°,使用mathcad可得如下波形圖矢量圖。
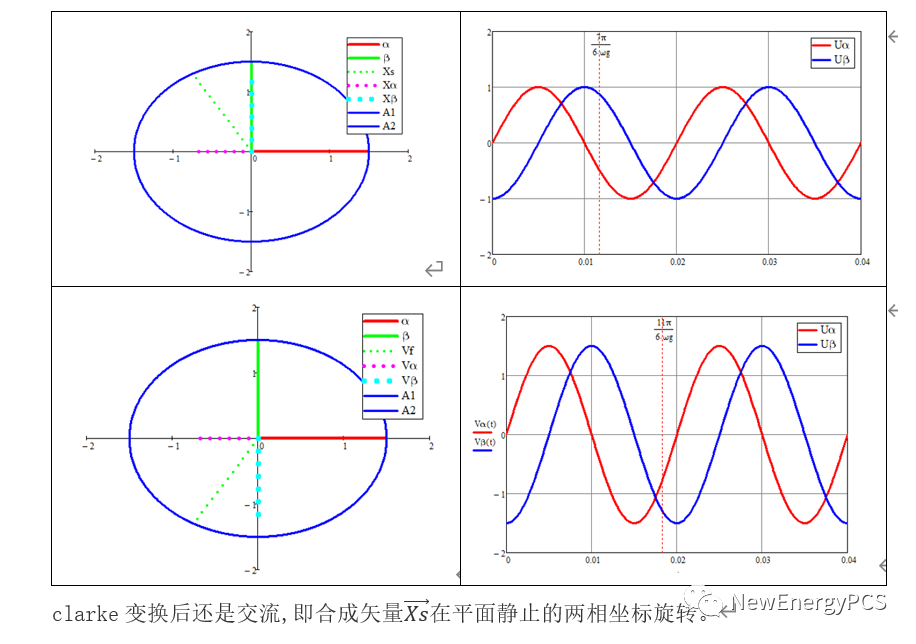
3.park變換分析推導過程
如果將原本平面靜止的兩相坐標以同平面旋轉矢量相同的角速度旋轉起來與其相對靜止,這時原來的旋轉矢量可以看做是相對于坐標靜止的直流分量。稱這兩分量為d,q分量。并且定義q軸超前d軸90°。2s/2r park變換既然是旋轉變換,就存在對齊問題與旋轉方向問題。那么就有α軸對齊d軸稱為d軸定向,或者α軸對齊q稱為q軸定向。
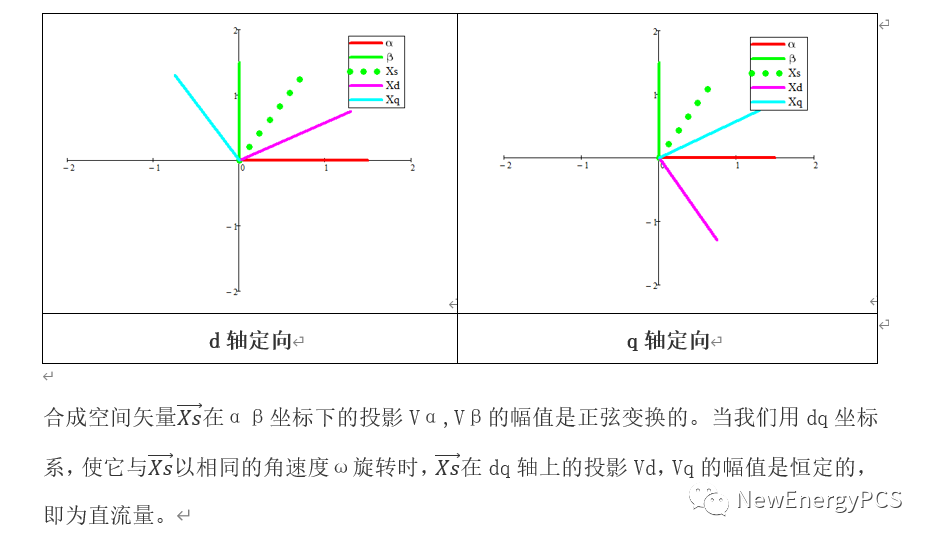
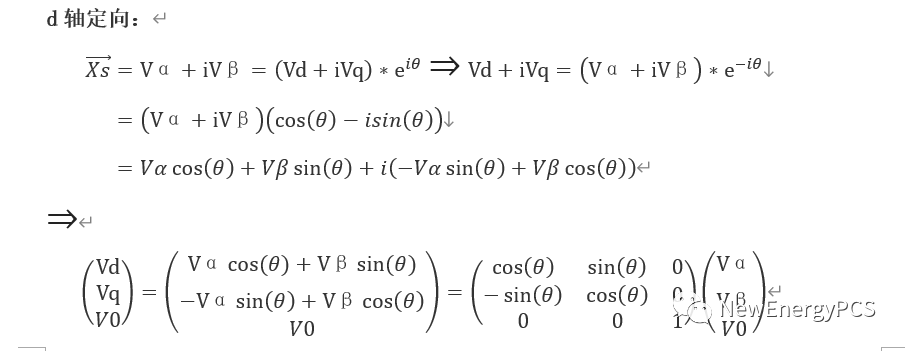
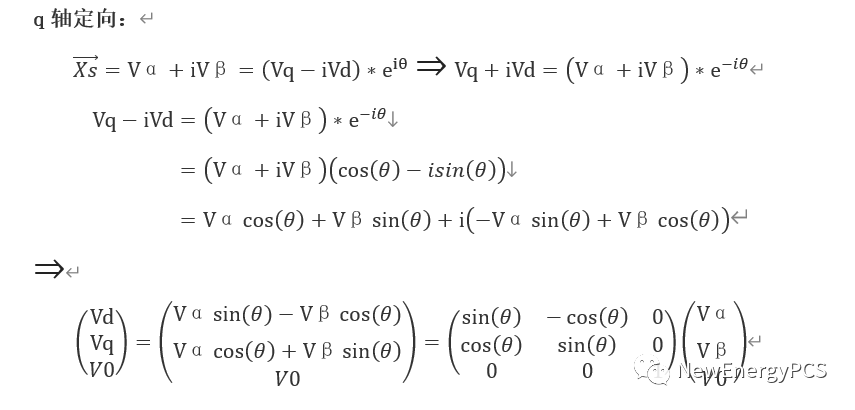
d軸定向mathcad仿真如下:
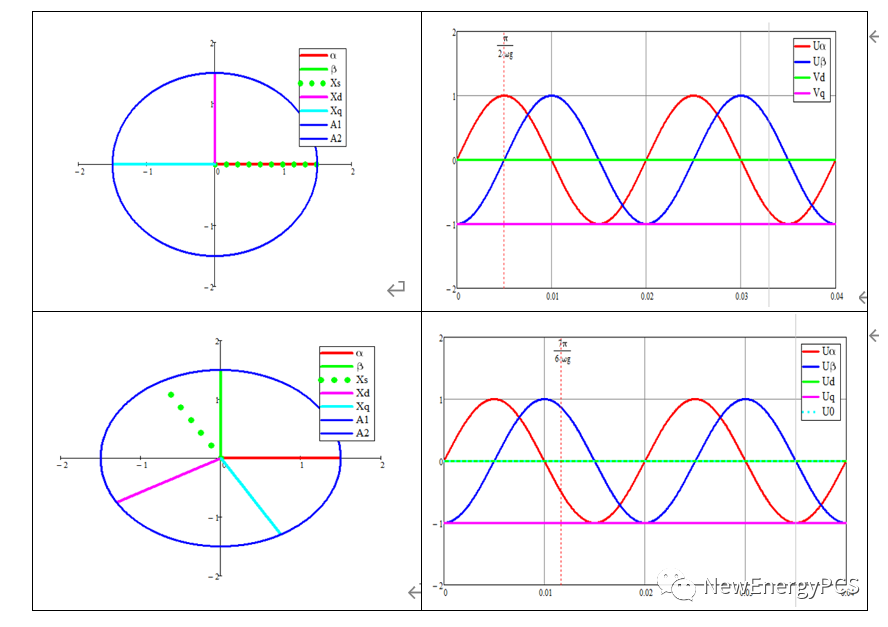
通過用d軸定向park變換矩得到了直流分量,但q軸分量為負,(從d軸定向的矢量圖看,q軸應該為正,應為q軸超前d軸90)。產生這個結果的原因是在clarke變換時,默認了β軸超前α90°。而實際上clarke變換時β軸滯后α 90°。
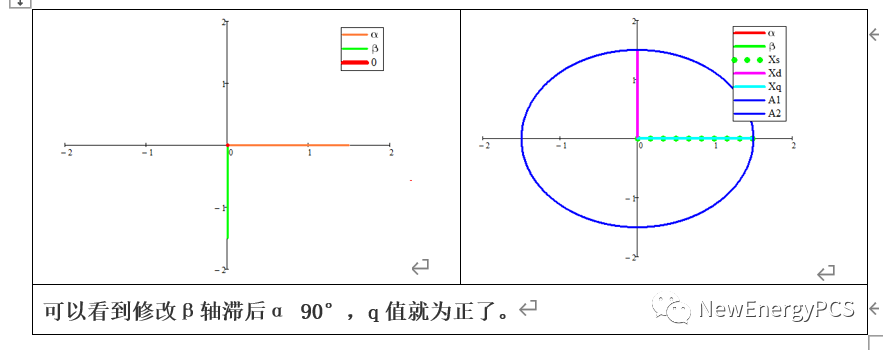
q軸定向mathcad仿真如下:
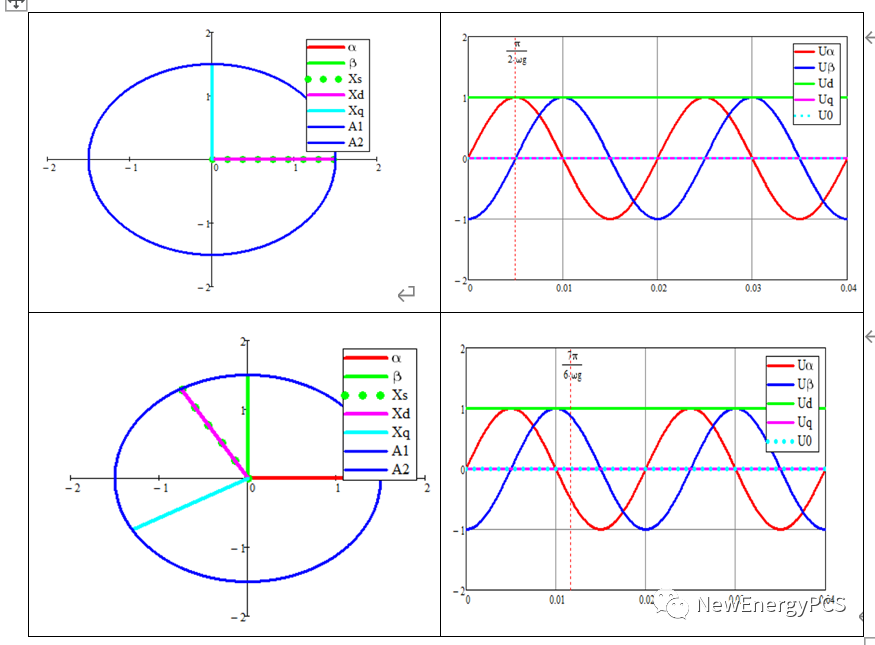
結論1:
使用不同的定義會有不同的clarke park變換矩陣,就需要做些匹配:如Clarke變換中正序改負序,鎖相環(PLL)輸出相角與park矩陣中的θ匹配。即PLL輸出角度作為park矩陣的θ角度時需要偏移90°。那么就要判斷三相系統為“正弦形式”或“余弦形式”,觀察系統三相波形與PLL輸出相位特征來判斷。
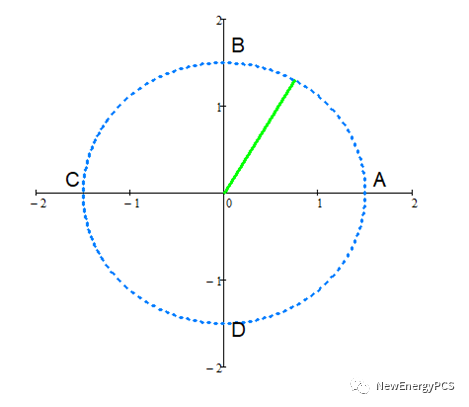
上圖為物理中描述物體簡諧運動的旋轉矢量法示意圖。當旋轉矢量的初始位置為圖中A點時,矢量旋轉一周其值將經歷A\\B\\C\\D的大小變化;當旋轉矢量位置為圖中D點時,,矢量旋轉一周其值將經歷D\\A\\B\\C的大小變化;此處稱A點初始位置為余弦形式,D點為初始位置時為正弦形式。
結論2:
三相系統(abc坐標系)的時域分量轉換為正交靜止坐標系(αβ)中的兩個分量。被稱為3S/2S,(三相靜止坐標轉換為二相靜止坐標)即clarke變換。將αβ坐標系中的兩個分量轉換為一個正交旋轉坐標系(dq)。也被稱為2s/2r,(二相靜止坐標轉換為二相旋轉坐標系)即park變換。連續實現這個兩個變換可將交流電流和電壓轉換為直流信號從而簡化計算,主要原因還是常用的控制器是經典的PI調節器,PI調節器可以對直流量進行無凈差調節,而交流量不行,所以將三相交流分量轉化為兩項直流分量做控制。
3.Clarke park逆變換分析推導過程:
由于PI控制器輸出是直流量, 那么就產生了上述相反的變換需求,即反park變換2r/2s,反park變換2S/3S。連續實現這個兩個變換可將直流電流和電壓轉換為交流信號,再將交流信號提供給PWM模塊作為參考信號進而控制。
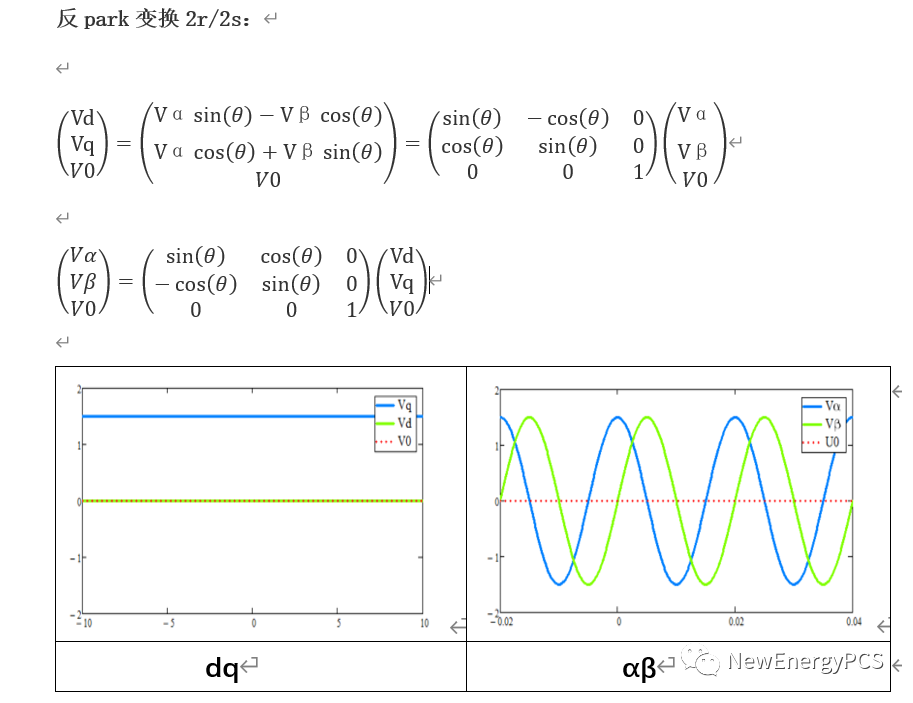
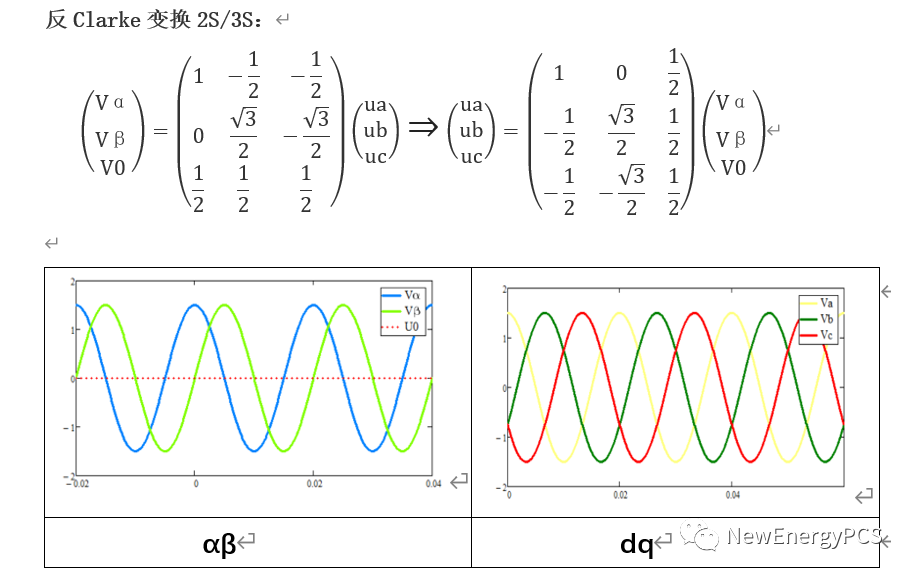
-
鎖相環
+關注
關注
35文章
583瀏覽量
87697 -
變換器
+關注
關注
17文章
2087瀏覽量
109147 -
MATLAB仿真
+關注
關注
4文章
176瀏覽量
19904 -
SVPWM控制
+關注
關注
0文章
26瀏覽量
5604 -
矢量控制器
+關注
關注
1文章
6瀏覽量
1218
發布評論請先 登錄
相關推薦
SVPWM原理推導與Mathcad建模的基本概念
基于載波的SVPWM發波計算Mathcad實例
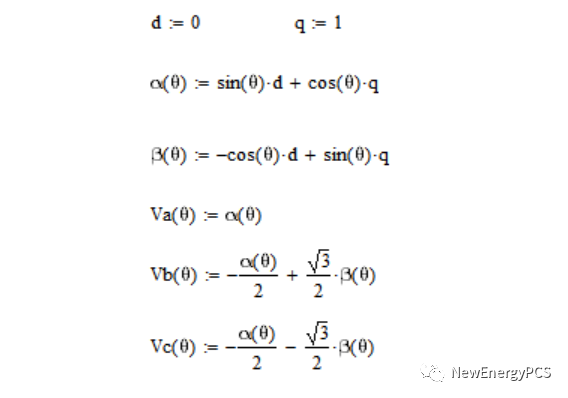
SVPWM原理推導與Mathcad建模控制實現




 SVPWM原理推導與Mathcad建模的坐標變換
SVPWM原理推導與Mathcad建模的坐標變換











評論