本文提出了一種新型的濾波器,其頻響具有直線特性,本文將詳細(xì)解釋如何推導(dǎo)這種特殊的濾波器。最后介紹基于Matlab的濾波器設(shè)計(jì)軟件,以低通為例,展示其功能。給出Github相關(guān)鏈接。
直線幅度濾波器特點(diǎn)和用途
直線幅度濾波器(Linear Amplitude Filter, LR Filter)濾波器本公眾號首次公開的一種濾波器,其幅頻特性在某一點(diǎn)上具有最佳直線幅度逼近特性,這種濾波器可以用于補(bǔ)償線纜插損,可以用于幅度均衡和濾波器兩用。
直線幅度濾波器
直線幅度濾波器是一類特殊的理想濾波器,其地位和矩形濾波器以及高斯濾波器相當(dāng),是無法通過多項(xiàng)式直接擬合得到的,只能通過函數(shù)逼近的方式得到,現(xiàn)在我們總結(jié)下現(xiàn)有濾波器設(shè)計(jì)。
總共有三類濾波器綜合如下(當(dāng)然這個(gè)圖還可以擴(kuò)展):
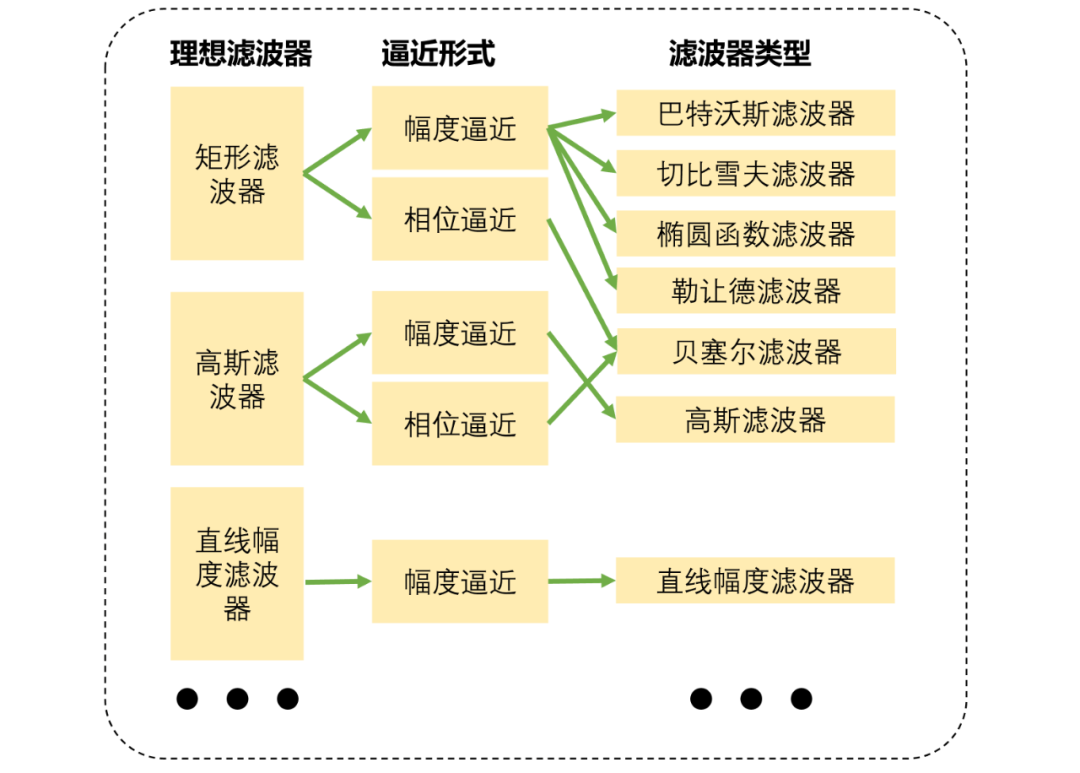
直線幅度濾波器綜合全流程如下:
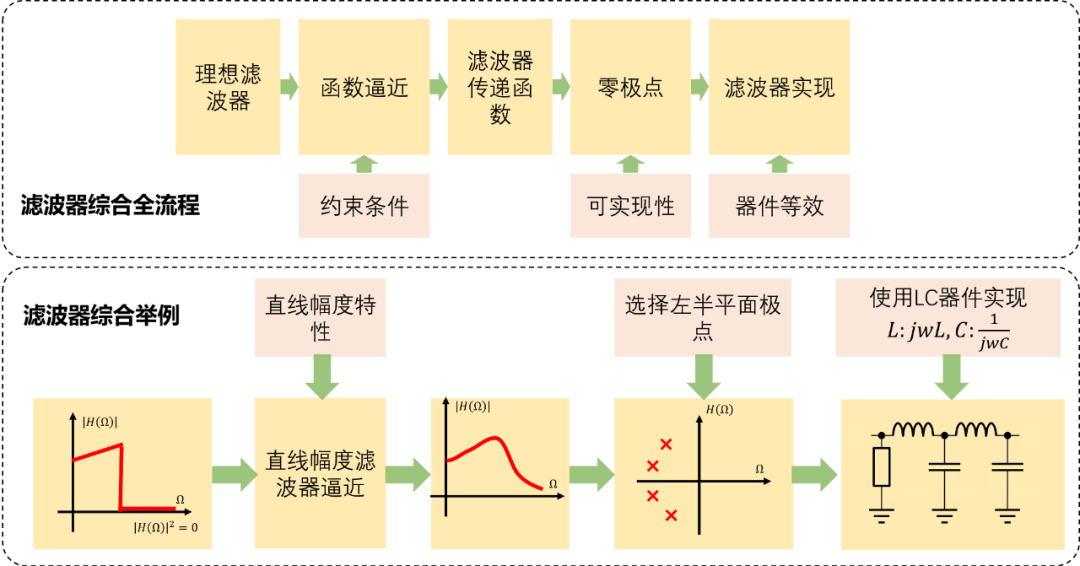
直線幅度濾波器逼近
這里定義直線幅度濾波器的幅頻響應(yīng)為:
其中為階直線幅度濾波器多項(xiàng)式。
約束
1,是階多項(xiàng)式(可實(shí)現(xiàn)性,在頻率增益為0)
2,(直線特性第一點(diǎn),在頻率為0的位置增益為,其中)
3,(直線特性第二點(diǎn),在頻率為1的位置增益為)
4,(直線濾波器帶寬定義,幅度最高點(diǎn)規(guī)定為1)
5,在通帶范圍內(nèi)逼近直線(直線幅度濾波器特征)
直線幅度逼近
首先需要澄清一點(diǎn)是定義,為了可實(shí)現(xiàn)性,因?yàn)橹挥卸囗?xiàng)式是偶次項(xiàng)才能實(shí)現(xiàn),偶次就意味著零點(diǎn)關(guān)于虛軸對稱,所以,最后濾波器極點(diǎn)就一定可以選擇到左半邊平面,是可以實(shí)現(xiàn)的。
照例我們定義:
是一個(gè)偶次多項(xiàng)式。
由約束2和3可以繪制出理想濾波器草圖:
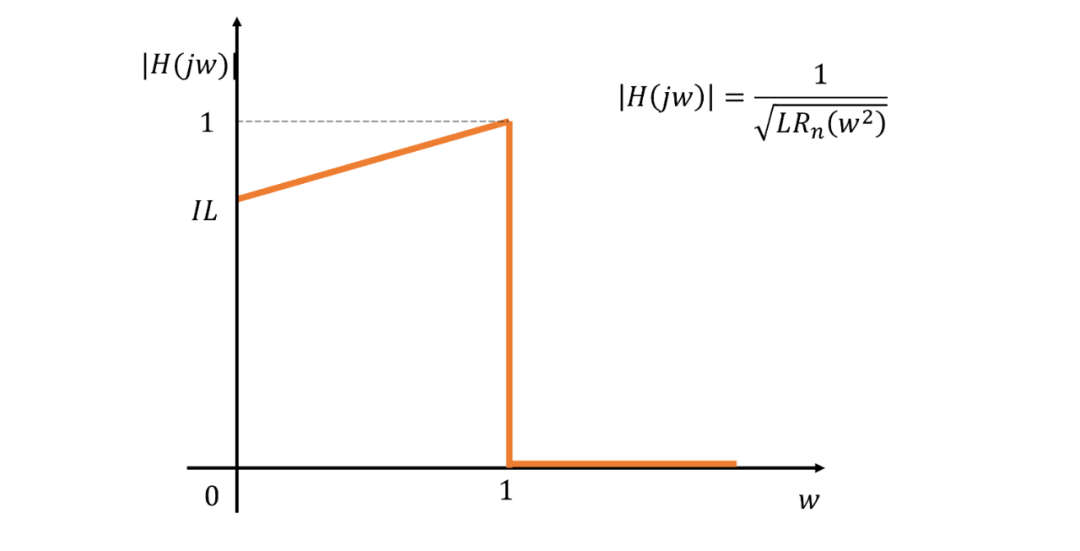
那么我們可以得到直線濾波器在帶寬范圍內(nèi)的直線表達(dá)式:
由約束1,是一個(gè)多項(xiàng)式,所以在區(qū)間范圍內(nèi),結(jié)合式和式,得到:
變量代換得到:
我們得到了理想濾波器在范圍內(nèi)的函數(shù)關(guān)系式,這里使用泰勒展開來進(jìn)行幅度逼近,其中展開的點(diǎn)可以在范圍內(nèi)隨意指定:
為簡單起見,這里將展開點(diǎn)定為,并且,使用wolfram alpha計(jì)算:
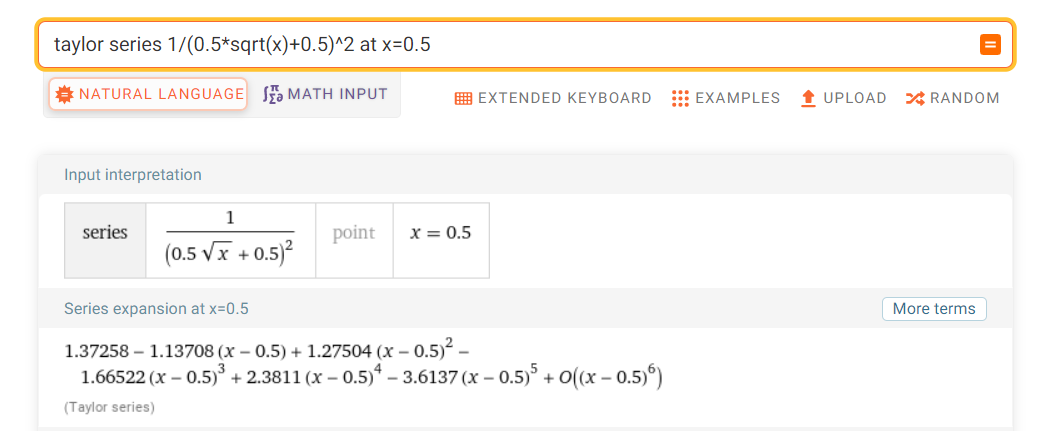
得到:
從泰勒逼近式我們可以看到,只能取偶數(shù),當(dāng)為奇數(shù)時(shí),最高次項(xiàng)是負(fù),當(dāng)頻率為無窮時(shí),,違反約束1。這里取,得到:
看看逼近效果:
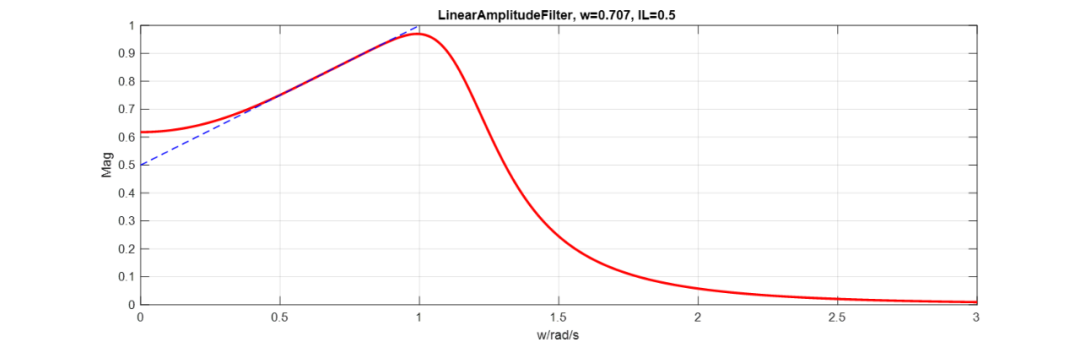
由于泰勒逼近只在有效,所以最終逼近后約束2,3,4將失效,所以需要對式和進(jìn)行處理,由約束3,4以及式可以得到多項(xiàng)式:
所以需要調(diào)整直線的截距來達(dá)到約束條件:
要依據(jù)式(8)和泰勒逼近(6)聯(lián)合得到所需的和展開點(diǎn),最終求解的方程為:
兩個(gè)方程兩個(gè)未知數(shù),式(8b)求解過程非常復(fù)雜,我們采用數(shù)值求解方案:這里采用了chebfun函數(shù)逼近庫來計(jì)算,得到時(shí),,,多項(xiàng)式為:
最終效果如下:
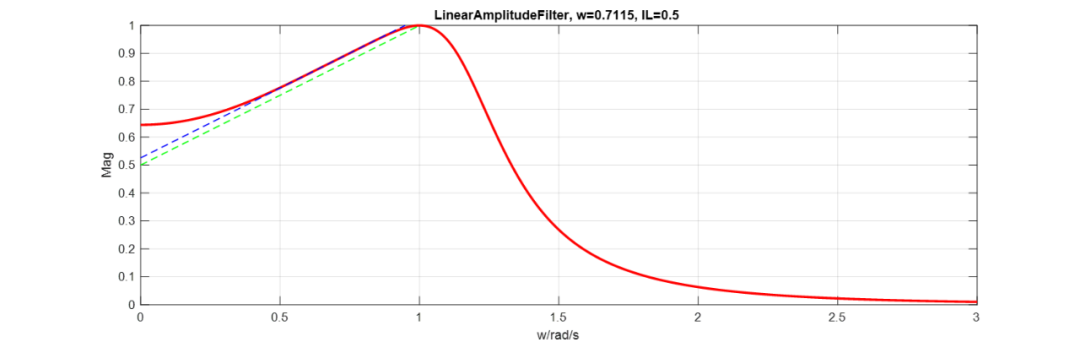
這個(gè)濾波器就是帶寬為1,斜率為0.5的4階直線幅度濾波器響應(yīng)。
那么當(dāng)階數(shù)增加,逼近效果怎樣呢,這里制作了階數(shù)從2到20階的幅度響應(yīng)動(dòng)圖(圖中對比了Butterworth頻響):
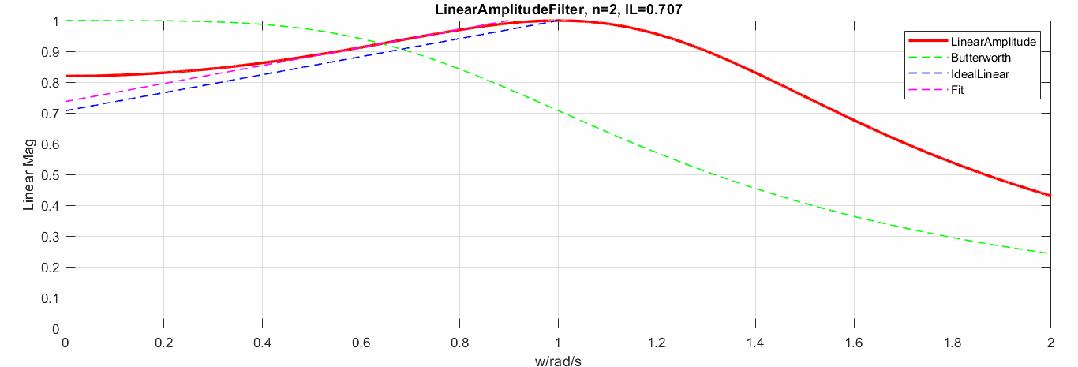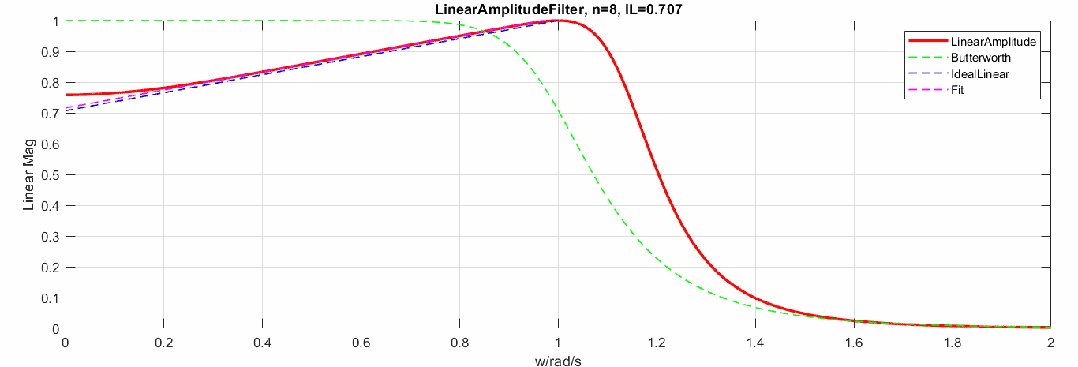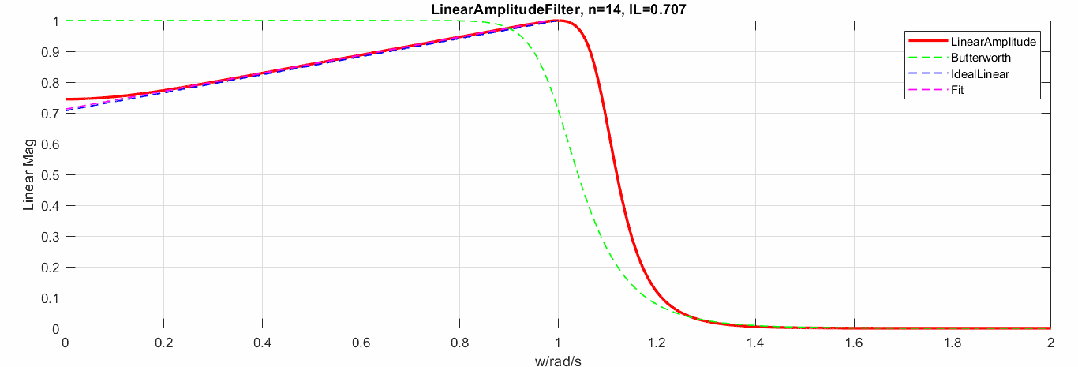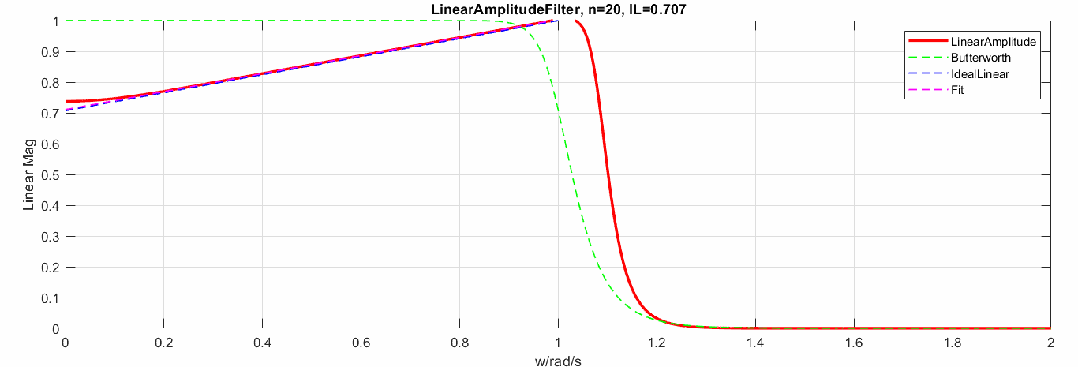
下圖是將幅度修改為dB,頻率軸還是線性:
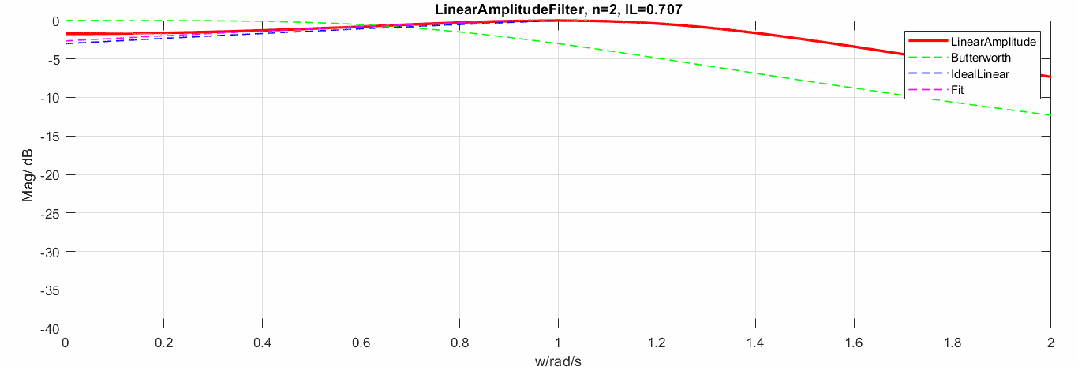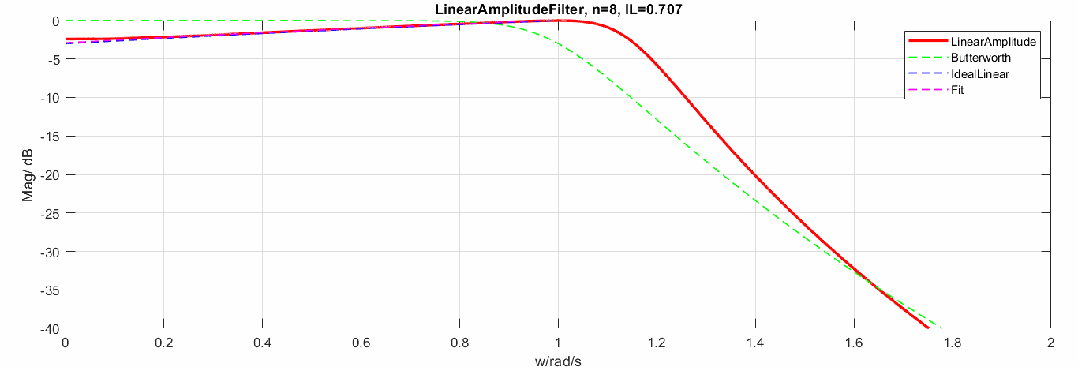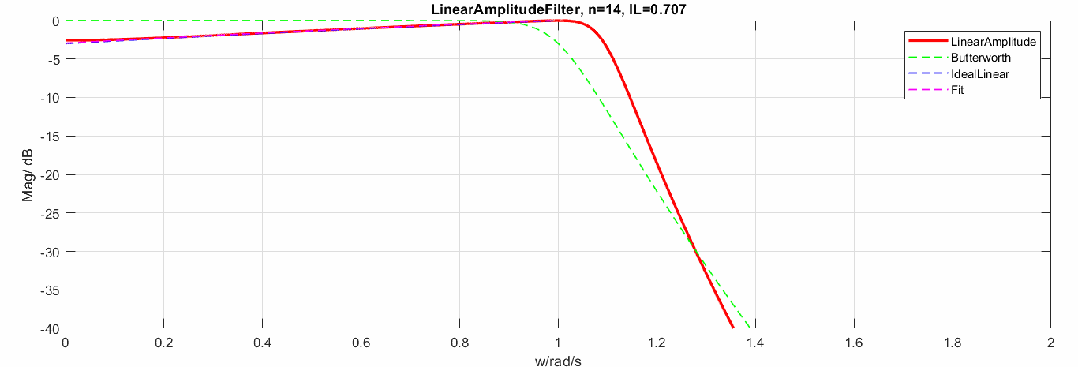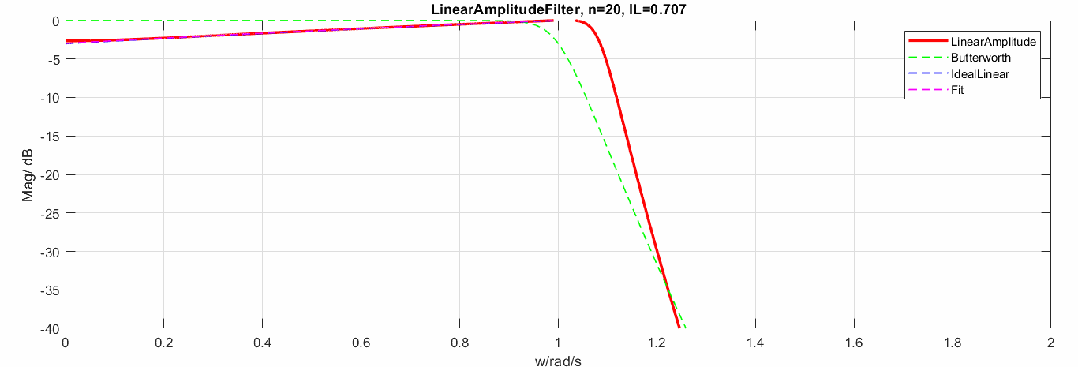
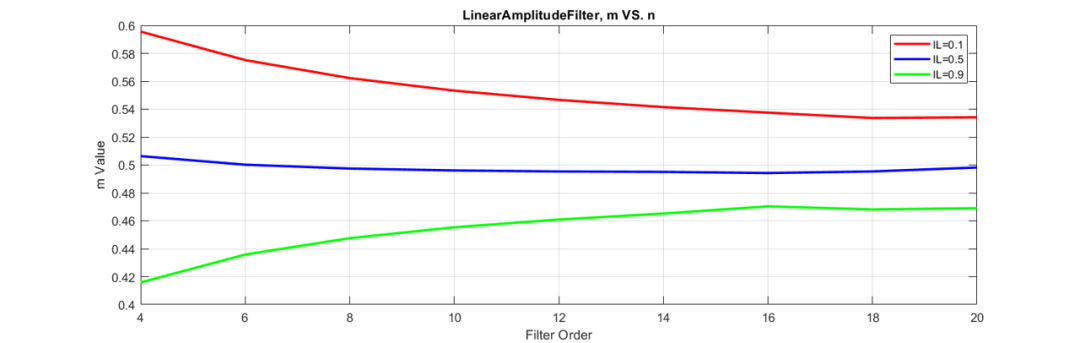
歸一化參數(shù)與階數(shù)的關(guān)系如下,當(dāng)階數(shù)升高,最終值會(huì)趨于0.5。圖中16階后曲線有偏移是因?yàn)橛?jì)算精度問題。
奇數(shù)階濾波器設(shè)計(jì)
目前還未找到一個(gè)有效的辦法解決奇數(shù)階直線幅度濾波器的設(shè)計(jì)(探索了幾個(gè)方案均不滿意)。
線性幅度濾波器多項(xiàng)式
和勒讓德濾波器類似,線性幅度濾波器多項(xiàng)式并沒有統(tǒng)一的公式來求解,這里采用了Matlab的符號計(jì)算工具來進(jìn)行求解:
%-------------------------------------------------------------------------- % Edited by bbl % Date: 2023-07-03(yyyy-mm-dd) % 線性幅度濾波器系數(shù)設(shè)計(jì) % 注意返回值低次在前,高次在后 %-------------------------------------------------------------------------- function [Ln] = funGenLinearAmpPoly(FilterOrder, IL) if mod(FilterOrder, 2) Ln = []; warning('FilerOrder must be even'); return; end % 使用chebfun函數(shù)計(jì)算m和b,使得在w=1處有單位增益和最大值 [m, b] = funLinearAmpGet_mb_chebfun(IL, FilterOrder); if FilterOrder > 20 dig = 100; else dig = 16; end syms x % 定義了直線幅度濾波器傳遞函數(shù) f = 1/((1-IL)*sqrt(x)+b)^2; a = sym(m); coeffsx = sym(0); for k = 0:FilterOrder kk = sym(k); % 使用在x=m處的麥克勞林展開得到系數(shù) coeffsx = coeffsx + vpa(subs(diff(f, x, kk) / factorial(k), x, a)*vpa((x-a)^kk, dig), dig); end polyx = coeffs(coeffsx); % 計(jì)算平方的系數(shù) Ln = vpa(zeros(1, length(polyx)*2-1), dig); Ln(1:2:end) = polyx; end
輸入,的到參數(shù):
>> [Ln] = funGenLinearAmpPoly(2, 0.707) Ln = [1.4882, 0, -0.9764, 0, 0.4882]
也即得到2階直線幅度濾波器多項(xiàng)式:
這里給出數(shù)值計(jì)算出的線性幅度濾波器前14階偶數(shù)濾波器多項(xiàng)式(注意這里不是特征多項(xiàng)式):
| 濾波器階數(shù) | |
|---|---|
| 2 | |
| 4 | |
| 6 | |
| 8 | |
| 10 | |
| 12 | |
| 14 |
在s平面取其左半邊極點(diǎn)得到前14階偶數(shù)線性幅度濾波器系數(shù)為(時(shí)幅度為1,時(shí)幅度為0.707):
| 濾波器階數(shù) | |
|---|---|
| 2 | |
| 4 | |
| 6 | |
| 8 | |
| 10 | |
| 12 | |
| 14 |
前14階線性幅度濾波器極點(diǎn)為(時(shí)幅度為1,時(shí)幅度為0.707):
| 濾波器階數(shù) | |||||||
|---|---|---|---|---|---|---|---|
| 2 | |||||||
| 4 | |||||||
| 6 | |||||||
| 8 | |||||||
| 10 | |||||||
| 12 | |||||||
| 14 |
線性幅度濾波器零極點(diǎn)
不同參數(shù)對線性幅度濾波器的極點(diǎn)影響如下圖所示,其極點(diǎn)分布推測和高斯濾波器一樣符合某種Szeg?曲線分布(其中兩個(gè)參數(shù)為0.5,另外一個(gè)參數(shù)從0.1掃描到0.9):
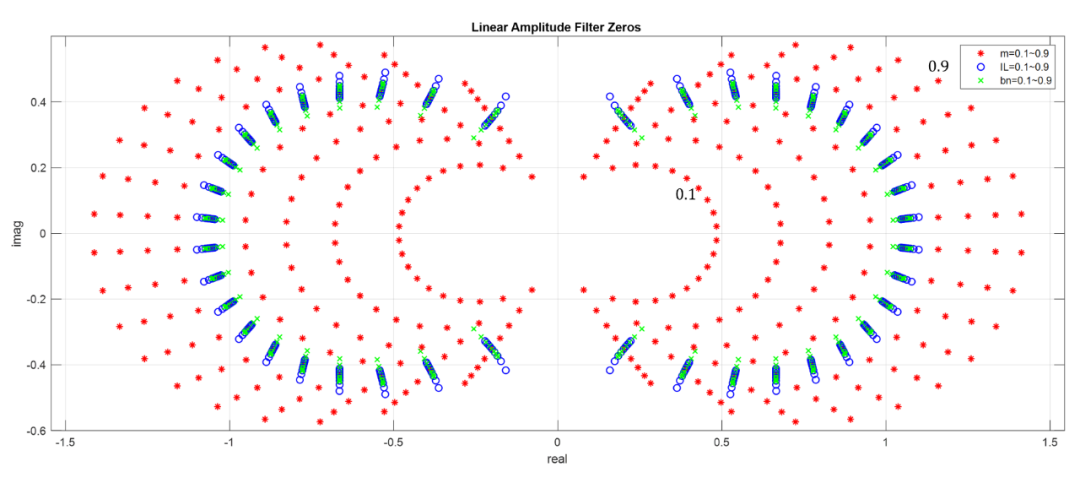
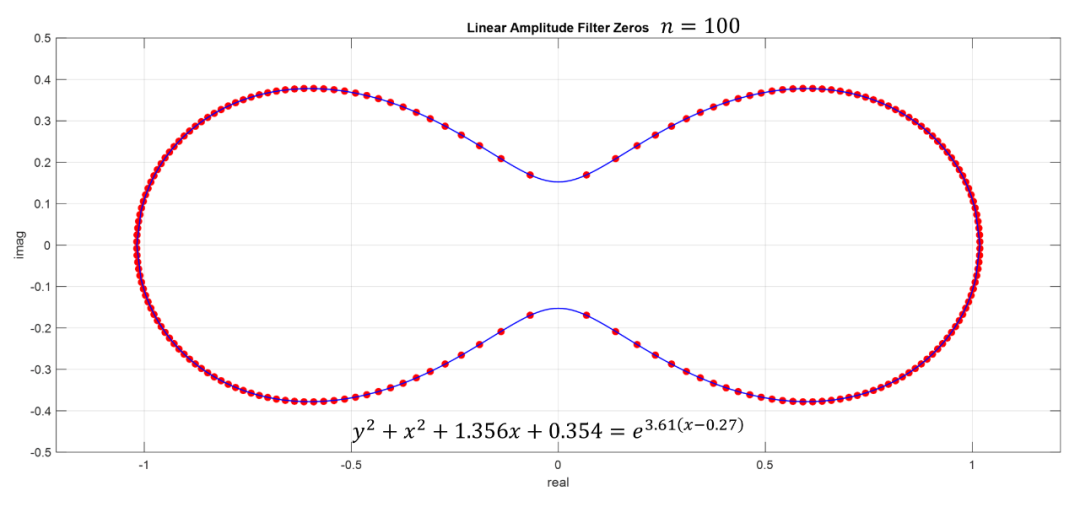
當(dāng)濾波器階數(shù)非常高時(shí)就極點(diǎn)分布規(guī)律就非常明顯(以下展示100階濾波器極點(diǎn)分布):
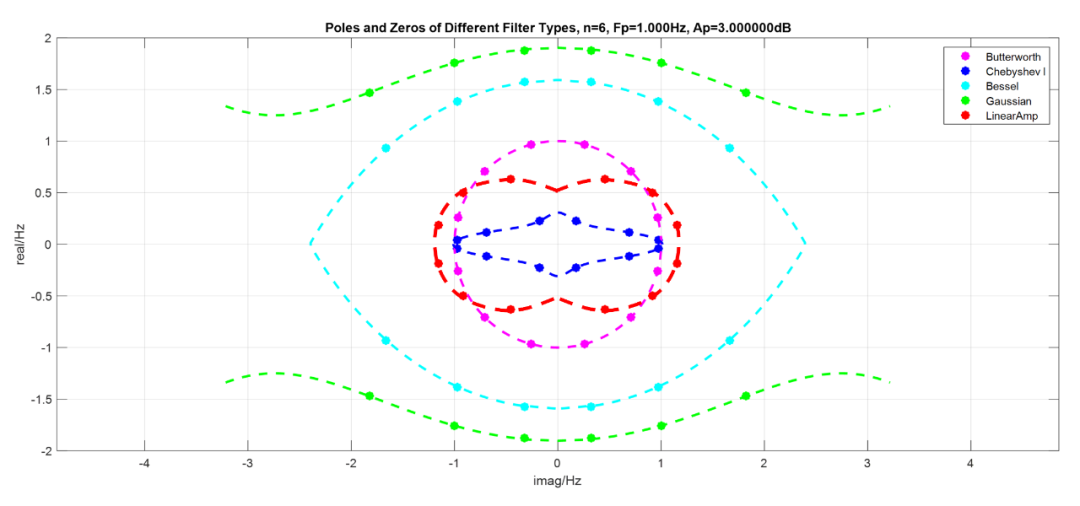
下圖是不同類型濾波器的零極點(diǎn)分布圖,紅色曲線和點(diǎn)是6階直線幅度濾波器極點(diǎn)分布:
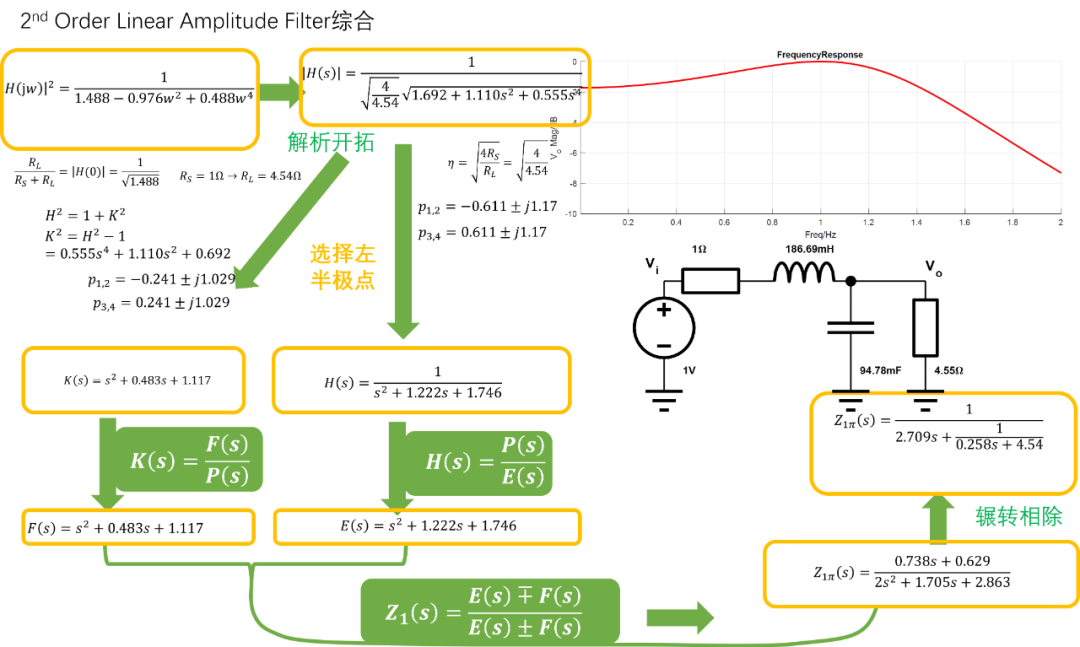
直線幅度濾波器綜合
這里僅使用全極點(diǎn)濾波器來綜合,列出一個(gè)簡單的2階3dB直線幅度濾波器綜合實(shí)例,以供參考:
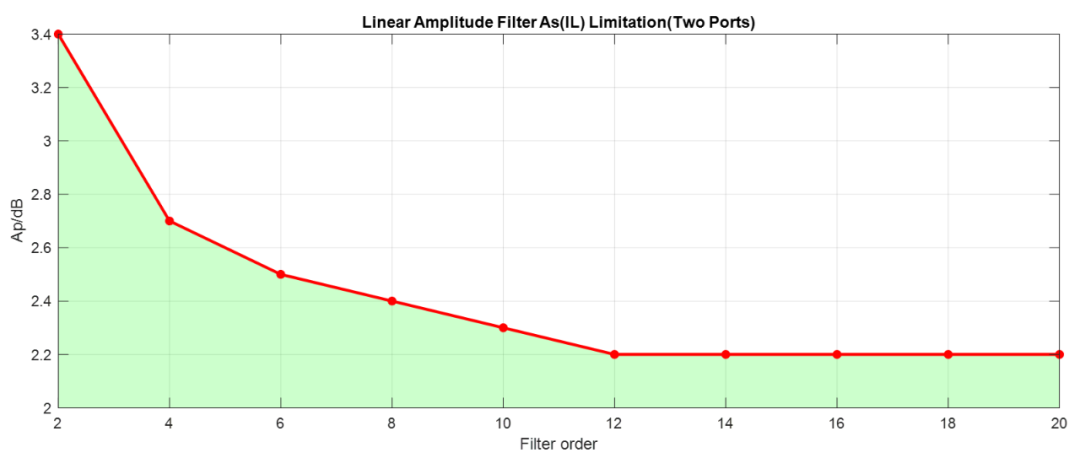
直線幅度濾波器IL(As)限制
對于上述線性幅度濾波器,由于綜合實(shí)現(xiàn)方面的限制,對于兩端匹配線性幅度濾波器,只能滿足特定IL(As)目標(biāo),比如對于2階線性幅度濾波器,其As必須小于3.4dB,對于10階線性幅度濾波器,其As必須小于2.3dB。
具體如下圖所示(圖中陰影部分是可實(shí)現(xiàn)的部分):
但是對于單端匹配狀態(tài)下的線性幅度濾波器,可以綜合出來的幅度調(diào)整范圍就寬很多,如對于終端開路的直線幅度濾波器,假設(shè),那么可以得到如下的綜合結(jié)果:
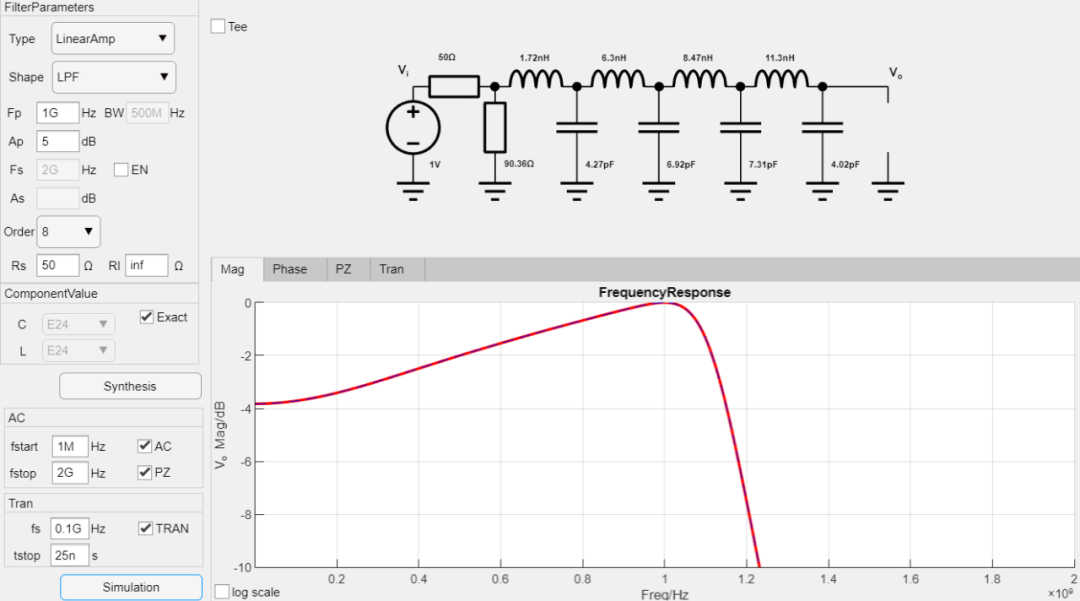
同樣的參數(shù)4種不同終端情況匯總?cè)缦拢梢跃C合出實(shí)際的電路出來:
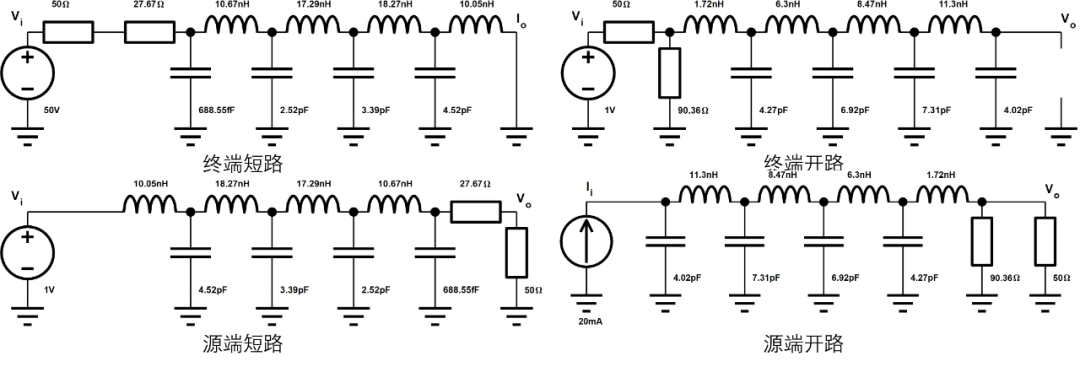
當(dāng)然兩端口直線幅度綜合限制也是有的,如下所示(圖中陰影部分是可實(shí)現(xiàn)的部分):
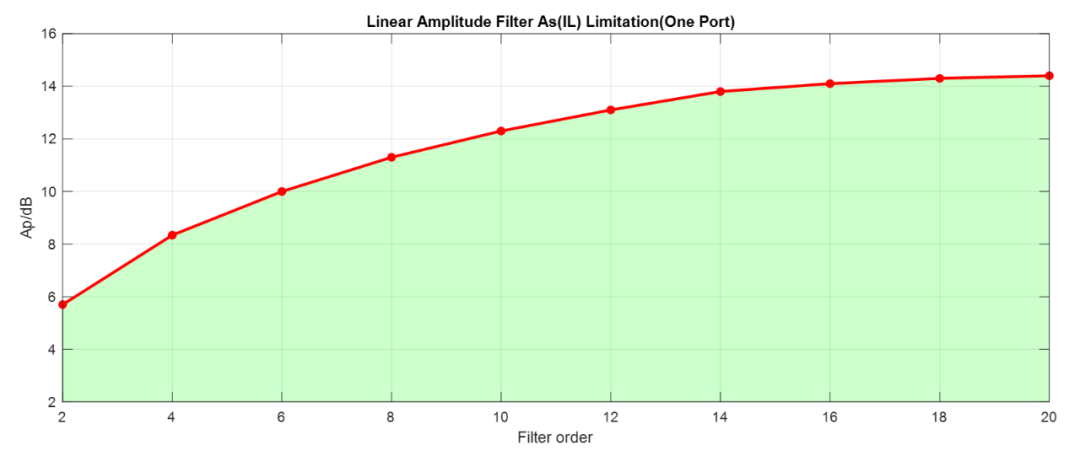
直線幅度濾波器設(shè)計(jì)軟件
基于Matlab的appdesign工具開發(fā)了一套濾波器設(shè)計(jì)軟件, 主要特點(diǎn)是:
支持直線幅度濾波器(Linear Amplitude Filter)、勒讓德濾波器(Legendre Filter)、高斯濾波器(Gaussian Filter)、貝塞爾濾波器(Bessel Filter)、橢圓函數(shù)濾波器(Elliptic/Cauer Filter)、切比雪夫?yàn)V波器(Chebyshev I)、逆切比雪夫?yàn)V波器(Chebyshev II, Inverse Chebyshev)、巴特沃斯濾波器(Butterworth)設(shè)計(jì)
支持4種不同濾波器通帶類型(LPF,HPF,BPF,BRF)設(shè)計(jì)
T型和PI型結(jié)構(gòu)濾波器隨意切換
可以設(shè)置阻帶衰減決定濾波器階數(shù)
可以設(shè)置通帶衰減來綜合濾波器
可以隨意配置負(fù)載和終端阻抗, 并支持一端接載(源端電阻短路, 源端電流源, 終端開路, 終端短路)設(shè)計(jì)
可以幅頻響應(yīng)分析、零極點(diǎn)分析、瞬態(tài)分析
可以顯示理想頻率響應(yīng)、零極點(diǎn)和實(shí)際仿真的的頻率響應(yīng)、零極點(diǎn)
可以支持實(shí)際標(biāo)準(zhǔn)器件逼近設(shè)計(jì)
LinearAmp LPF設(shè)計(jì)舉例
設(shè)計(jì)一款-2.0dB截止頻率為1GHz, 8階低通線性幅度濾波器,輸入輸出阻抗為50歐姆,設(shè)計(jì)過程如下:
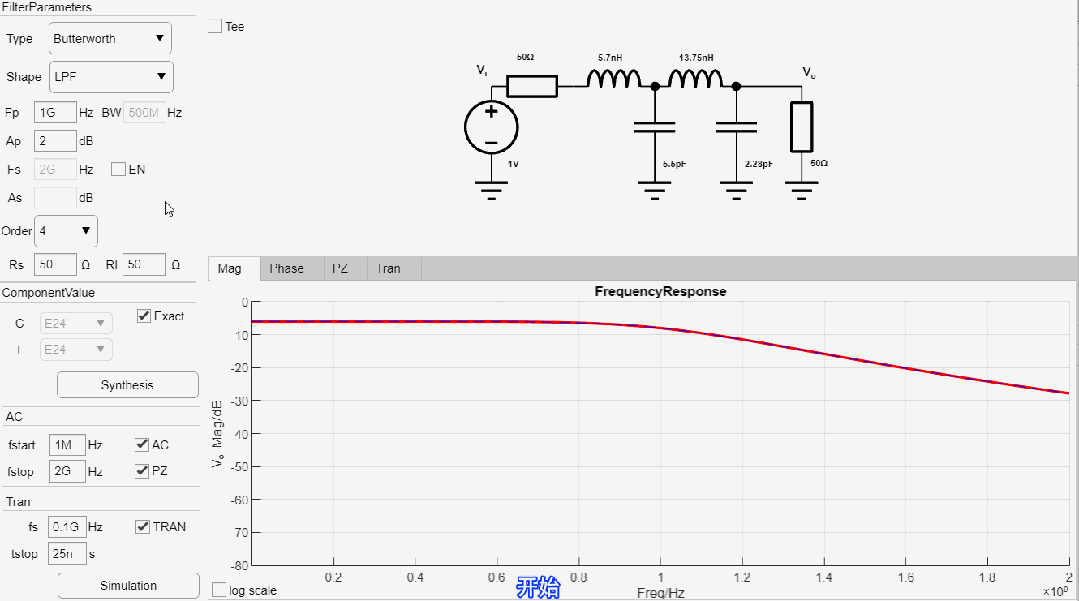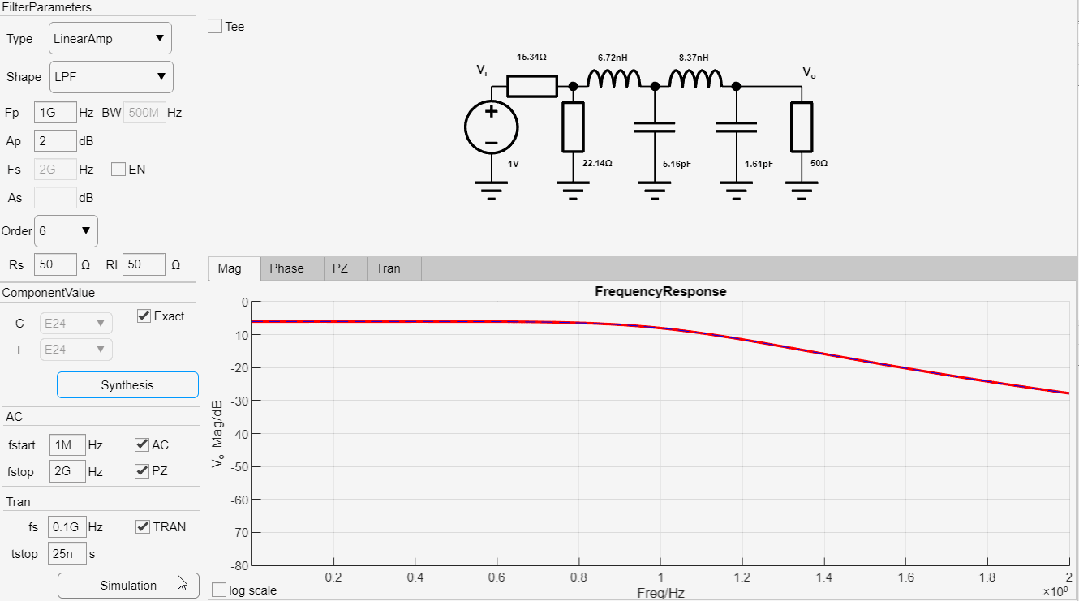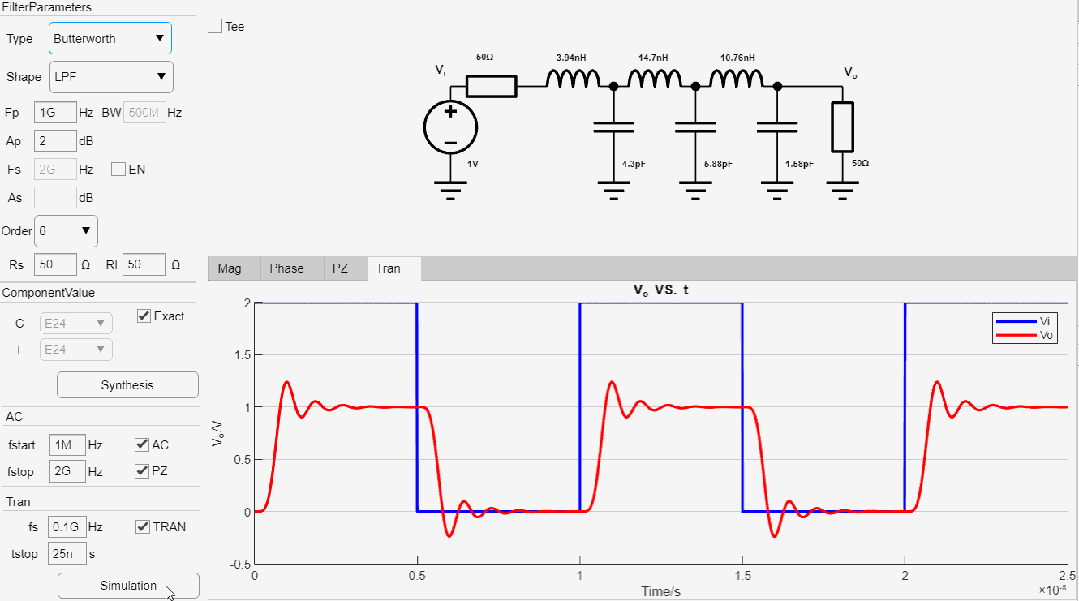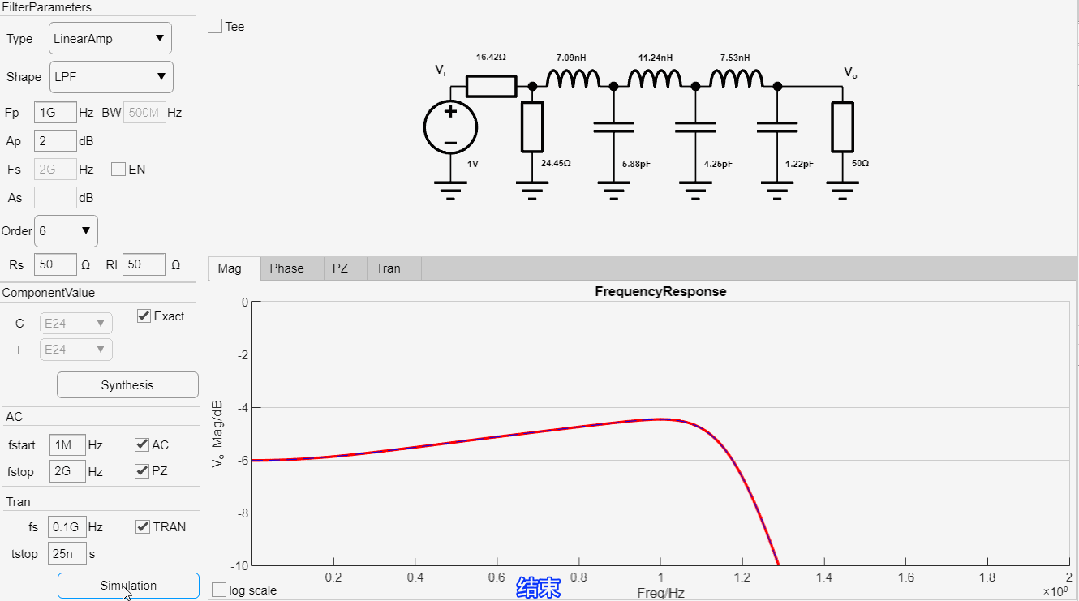
最終設(shè)計(jì)參數(shù)如下:
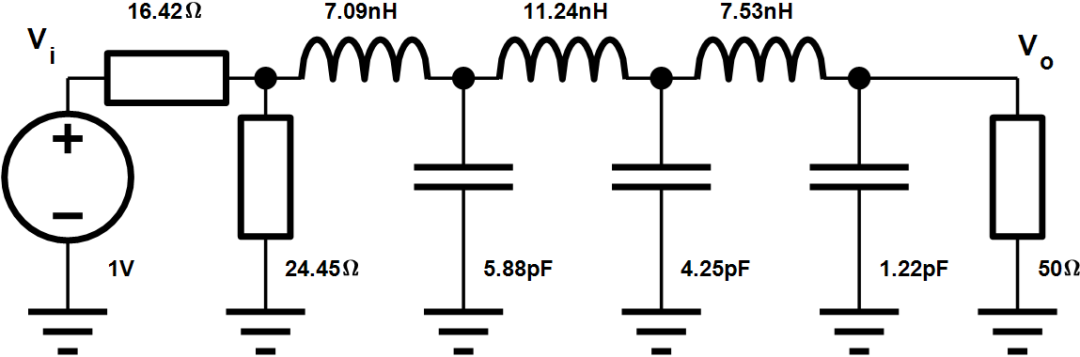
線性幅度濾波器瞬態(tài)仿真結(jié)果:
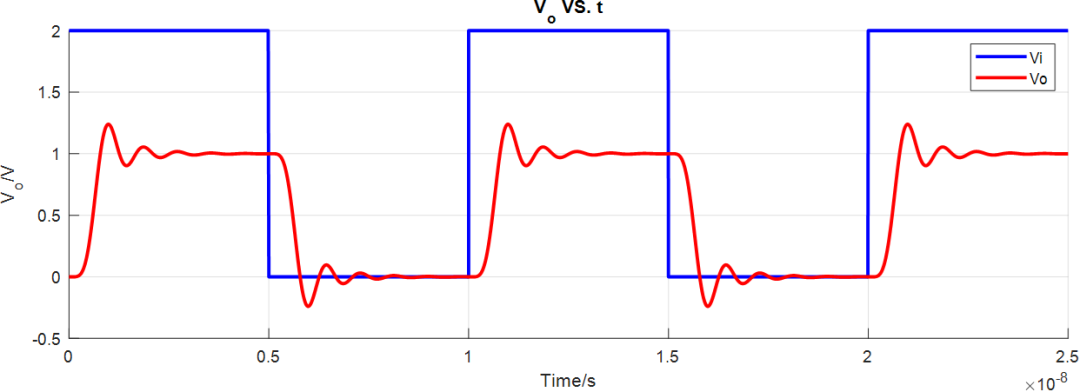
線性幅度濾波器AC仿真結(jié)果:
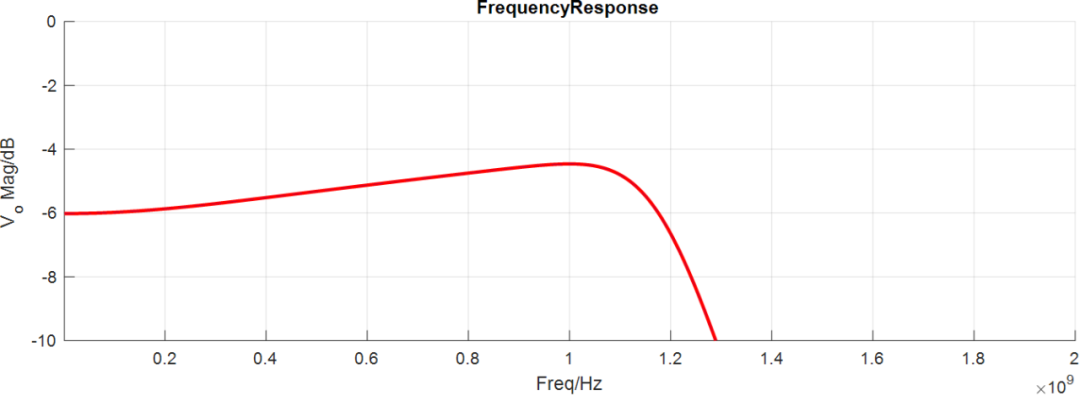
程序的Matalb源碼已經(jīng)上傳GitHub中(https://github.com/etools361/MatlabLinearAmpFilterDesignApp),有興趣的同學(xué)可以下載試用體驗(yàn),當(dāng)然也歡迎技術(shù)交流。
展望
本文只提出了偶數(shù)階濾波器的梯形網(wǎng)絡(luò)實(shí)現(xiàn)方法,還可探索奇數(shù)階濾波器設(shè)計(jì);
理論上還存在多種不同實(shí)現(xiàn)方案,比如使用電阻和電容網(wǎng)絡(luò)實(shí)現(xiàn);
兩端匹配衰減幅度的范圍也可以進(jìn)一步拓寬;
匹配特性還可改善,比如將對地電阻衰減更換為衰可以進(jìn)一步改善駐波;
審核編輯:湯梓紅
-
matlab
+關(guān)注
關(guān)注
182文章
2963瀏覽量
230149 -
濾波器
+關(guān)注
關(guān)注
160文章
7727瀏覽量
177670 -
計(jì)算
+關(guān)注
關(guān)注
2文章
444瀏覽量
38733 -
GitHub
+關(guān)注
關(guān)注
3文章
466瀏覽量
16384
原文標(biāo)題:模擬無源濾波器設(shè)計(jì)(十一)-LinearAmplitude濾波器設(shè)計(jì)詳解
文章出處:【微信號:電路設(shè)計(jì)小工具,微信公眾號:電路設(shè)計(jì)小工具】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
全文詳解IIR濾波器原理與設(shè)計(jì)方法

詳解FIR濾波器和IIR濾波器的區(qū)別
詳解FIR濾波器和IIR濾波器區(qū)別
濾波器有幾種?四種濾波器之間對比詳解
帶通濾波器電路圖大全(三款帶通濾波器電路設(shè)計(jì)原理圖詳解)
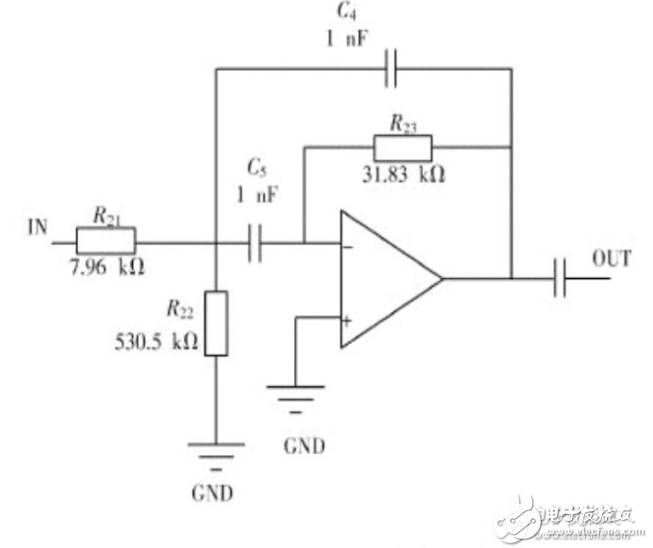
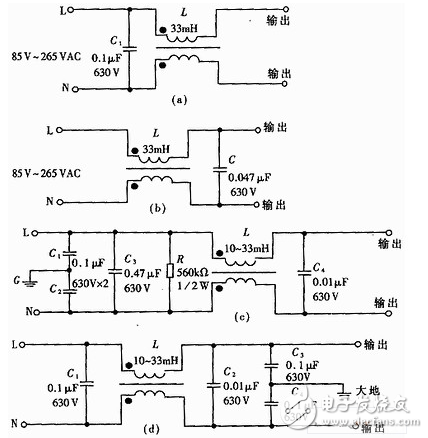
電源濾波器電路圖大全(八款電源濾波器電路設(shè)計(jì)原理圖詳解)
220v電源濾波器電路圖大全(五款220v電源濾波器電路設(shè)計(jì)原理圖詳解)
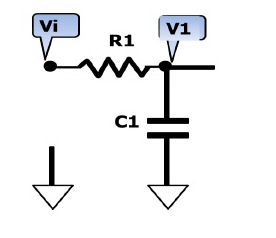
一文詳解低通濾波器




 LinearAmplitude濾波器設(shè)計(jì)詳解
LinearAmplitude濾波器設(shè)計(jì)詳解










評論