晶格的周期性

原胞和基矢晶格的共同特點是具有周期性，因此晶格周期性可以用原胞和基矢來描述。原胞是晶體中體積最小的周期性重復單元，當它平移布拉維格子所有可能的格矢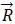時，將精確地填滿整個空間，沒有遺漏，也沒有重疊。

對某一晶格，盡管習慣上常取三個不共面的最短格矢為基矢，但原則上基矢的取法并不唯一，原胞亦有多種取法。但無論如何選取，原胞均有相同的體積，平均每個原胞只包含一個格點。在有限大的晶體中所含原胞數和格點數相等。人們常選用維格納—塞茨原胞，簡稱WS原胞，以晶格中某一格點為中心，作與其近鄰的格點連線的垂直平分面，以該點為中心所圍成平面的最小體積屬于該點的WS原胞。顯然，屬于某一格點的WS原胞由空間內最接近該點的區域所構成。圖1給出了一個二維布拉維格子的WS原胞，它的構造中不涉及對基矢的任何特殊選擇，所以它與相應的布拉維格子有完全相同的對稱性，因此也將WS原胞稱為對稱化原胞。

圖1二維布拉維格子的WS原胞

由于晶格的周期性，可以把基矢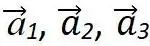為三個棱邊所組成的平行六面體作為晶格結構的重復單元，它們平行地堆積在一起，互相沒有交疊，可以充滿整個晶格。這樣的結構重復單元稱為單胞。由子格點處在平行六面體的頂角上，每一原胞共有八個頂角面每一頂角又為八個原胞所共有，故每個單胞只含有一個格點，它是體積最小的結構重復單元，其體積為:?

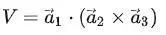
這恰好是平均每一格點所占的體積。除了周期性外，每種晶體還有自己特殊的對稱性，為了同時反映晶格的對稱性，往往選取體積較大的結構重復單元，稱為晶胞。

2

簡單立方晶格

原子球在一個平面內呈正方排列，如圖2所示。這樣的原子層疊加起來得到簡單立方格子，用原點表示原子的位置，即得到其相應的晶格結構。

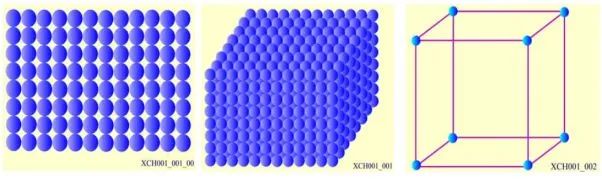
圖2 簡單立方格子

簡單晶格中，某一個單胞只包含一個原子，所有的原子在幾何位置和化學性質上是完全等價的。堿金屬具有體心立方晶格結構；Au、Ag和Cu具有面心立方晶格結構，它們均為簡單晶格，原胞中只包含一個原子。

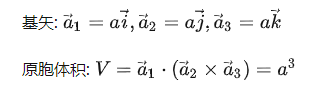
3

體心立方晶格

體心立方晶格結構如圖3所示，體心立方原子球排列的方式可以表示為: AB AB AB……, 體心立方晶格中，A層中原子球的距離等于A-A層之間的距離，要做到這一點需A層原子球的間隙:△=0.31r0（r0：原子球的半徑）。具有體心立方晶格結構的金屬: Li、Na、K、Rb、Cs、Fe等。

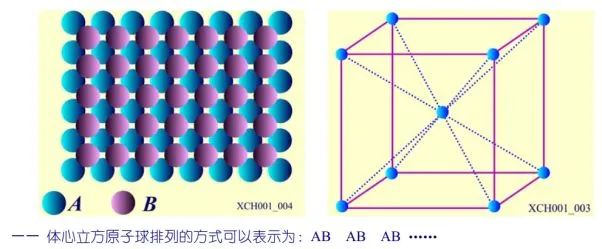
圖3 體心立方格子

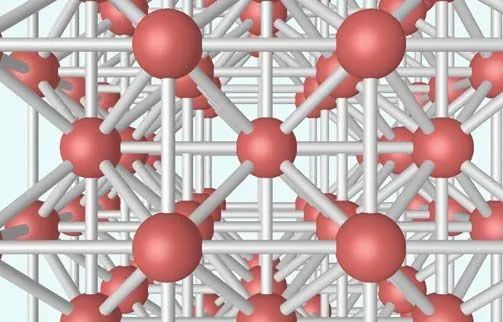
圖4 體心立方格子晶胞

體心立方晶格的晶胞如圖4所示，除頂角上有格點外，在立方體的中心處還有一格點，故稱為體心立方。晶胞的邊長為a，稱為晶格常數。將這種晶胞平行堆積起來就得到體心立方晶格，平均每個晶胞含有兩個格點。每個晶胞的頂角都是相鄰晶胞的心，所有格點都是等價的， 故體心立方晶格是一種布拉菲晶格，其單胞的基矢可以選為:

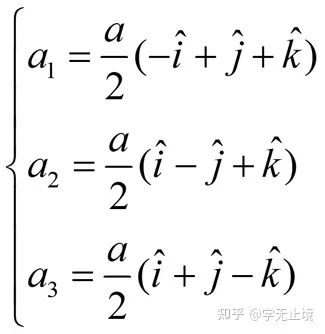
式中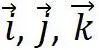?為直角坐標系的三個單位矢量。單胞的體積為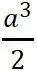?，是晶胞體積的一半。

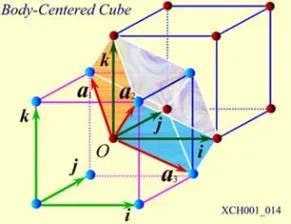
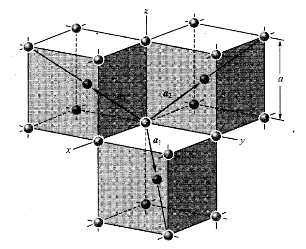
圖5 帶有直角坐標系的體心立方格子

4

六角密排晶格

原子在晶體中的平衡位置，排列應該采取盡可能的緊密方式，對應于結合能最低的位置。一個原子周圍最近鄰的原子數，可以被用來描寫晶體中粒子排列的緊密程度，這個數稱為配位數。晶體中最大配位數與可能配位數的數目不同。晶體由全同的一種粒子組成，將粒子看作小圓球，則這些全同的小圓球最緊密的堆積稱為密堆積，密堆積所對應的配位數，就是晶體結構中最大的配位數。全同的小圓球平鋪在平面上，任一個球都與6個球相切。每三個相切球的中心構成一個等邊三角形，并且每個球的周圍有6個空隙，這樣構成的一層，計為A層，第二層也是同樣的鋪排，計為B層，第三層也是同樣的鋪排，計為C層。把B層的球放在A層相間的3個空隙里，第二層的每個球和第一層的三個球緊密相切，如圖6所示。

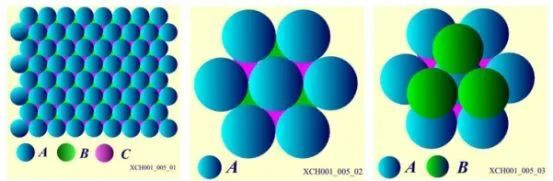
圖6密堆積排列

第三層C層有兩種不同的堆法。C層原子排列之一：六角密排晶格。原子球排列方式為: AB AB AB……，如圖7所示。在層的垂直方向是6對稱性的軸，這個垂直方向的軸就是六角晶系中的c軸，Be、Mg、Zn、Cd具有六角密排晶格結構。

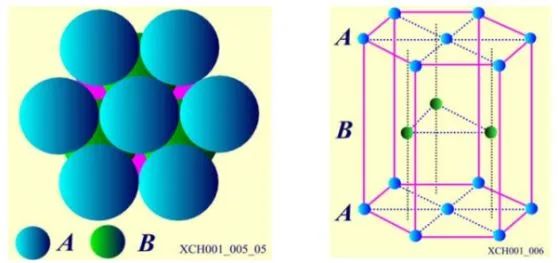
圖7 六角密排晶格

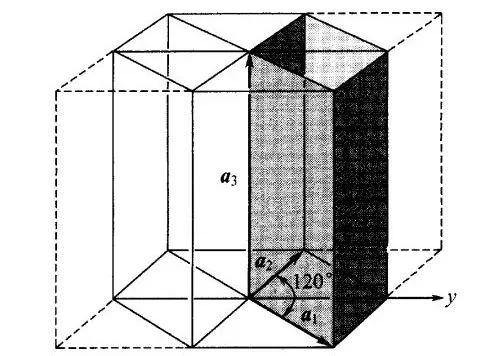
圖8 六角晶系的原胞與六角對稱棱柱的關系，其中a1=a2≠a3。

5

面心立方晶格

C層原子排列之二: 面心立方晶格，原子球排列方式為: ABC ABC ABC，如圖9所示。層的垂直方向是對稱性為3的軸，就是立方體的空間對角線。Cu、Ag、Au、AI具有面心立方晶格結構;

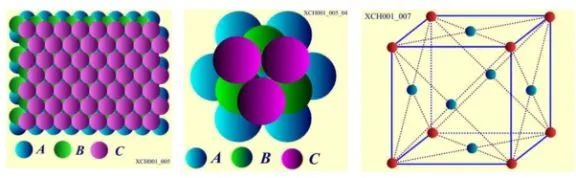
圖9 面心立方晶格

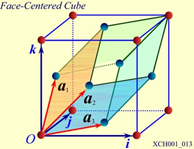
圖10 面心立方晶格的晶胞

圖10為面心立方晶格的晶胞。除頂角外，在立方體六個面的中心處還有一個格點，故稱為面心立方。每個面為兩個相鄰的晶胞所共有，每個面心格點只有二分之一是屬于一個晶胞，而處于頂角上的每個格點只有八分之一屬于一個晶胞，所以每個面心立方晶胞只含有4個格點。把晶胞平行堆積起來不難看出，處于面心和頂角上的格點是等價的，每一格點周期的情況完全相同，面心立方晶格也是一種布拉菲晶格。其原胞的基矢可以選為：

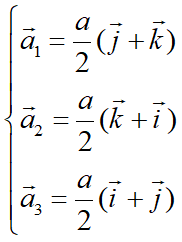
原胞的體積:

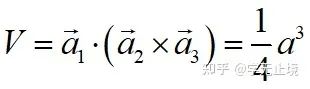
單胞基矢:

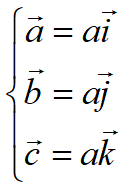
單胞的體積:

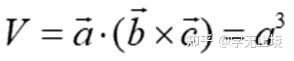
原胞的體積為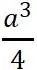，是單胞體積的四分之一 。因為原胞的選擇不是唯一的，所以我們也可以選擇對稱性更高的原胞。例如。以每一格點為中心，作它與最近鄰和次近鄰格點聯線的垂直平分面，這些面圍成一個封閉的多面體，晶格將被這些多面體平行堆積所充滿，每個多面體就是一個原胞，稱為威格納—賽茲原胞。圖是二維布拉菲晶格的威格納—賽茲原胞，每個維格納賽茲原胞只含一個格點，每個格點都位于原胞的中心，它的對稱性顯然要比通常的平行六面體原胞高。面心立方晶格的威格納賽茲原胞為十二面體，而體心立方晶格的威格納賽茲原胞為截角八而體，即十四面體。

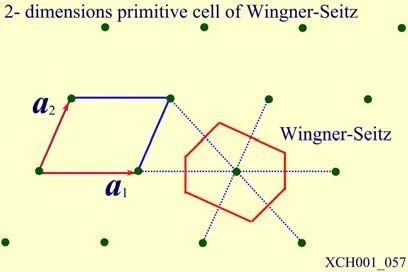
圖11 維格納賽茲原胞

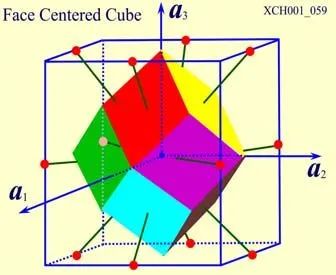
圖12 面心立方晶格的威格納賽茲原胞

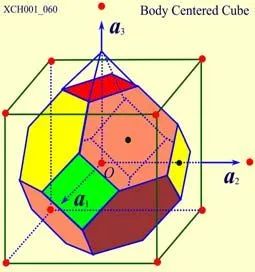
圖13 體心立方晶格的威格納賽茲原胞

綜上所述，晶體結構的周期性是通過布拉菲晶格來體現的，只要把基元按同樣規律安放在格點上就得到實際的晶體結構，每一個布拉菲格點和一個原胞相對應，原胞的平行堆積充滿整個晶格，原胞中的任一點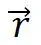與另一原胞的相應點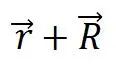應有相同的物理性質，這就是晶格的平移對稱性。顯然，嚴格的平移對稱性只能在無限大的晶體中才能實現，但實際晶體的尺寸通常比晶格周期大好幾個數最級，故除了專門研究表面的性質外，可以近似地把晶體看成是無限大。

6

金剛石晶格結構

金剛石由碳原子構成，在一個面心立方原胞內還有四個原子，這四個原子分別位于四個空間對角線的四分之一處。一個碳原子和其它四個碳原子構成一個正四面體。如圖14所示分別為金剛石和石墨晶格結構。重要的半導體材料如Ge、Si等，都有四個價電子，它們的晶體結構和金剛石的結構相同，如圖15所示。

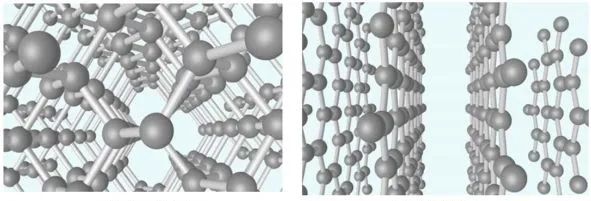
圖14 金剛石（左）和石墨烯（右）結構

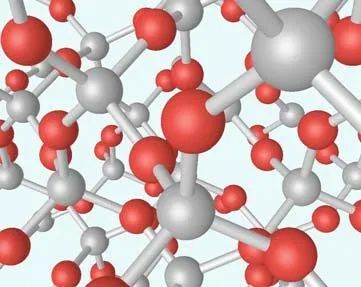
圖15 硅晶體結構

7

幾種化合物晶體的晶格

NaCI晶體的結構如圖16所示。氯化鈉由Na+和Cl?結合而成，是一種典型的離子晶體， Na+構成面心立方格子，Cl?也構成面心立方格子。兩個面心立方子晶格各自的原胞具有相同的基矢，只不過互相有位移差。

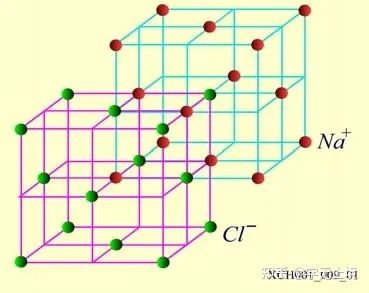
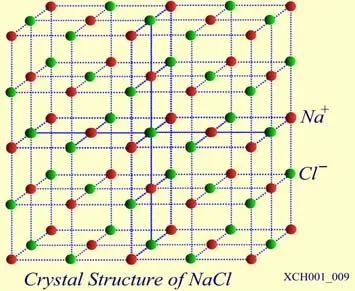
圖16 NaCI晶體的結構

CsCl晶體的結構：CsCl是一種典型的離子晶體，其結晶學原胞如圖17所示。CsCl結構是由兩個簡單立方的子晶格彼此沿立方體空間對角線位移二分之一的長度套構而成。

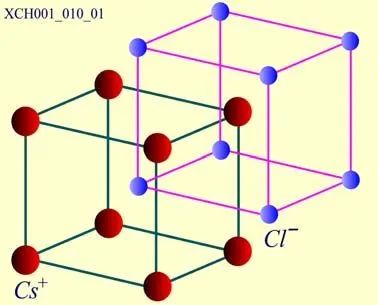
圖17 CsCl晶體的結構

ZnS晶體的結構：立方系的硫化鋅具有和金剛石類似的結構，其中硫和鋅分別組成面心立方結構的子晶格，沿空間對角線位移四分之一的長度套構而成，這樣的結構統稱閃鋅礦結構。如圖18所示。許多重要的化合物半導體，如銻化銦（InSb）、砷化稼（GaAs）等都是閃鋅礦結構，在集成光學上很重要的。

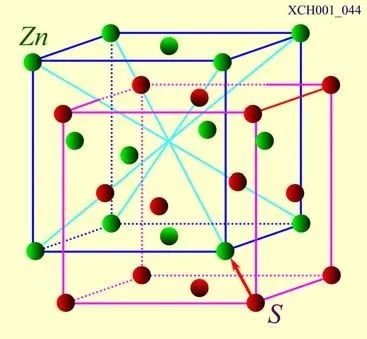
圖18 ZnS晶體的結構

鈣鐵礦結構: 指鈦酸鈣(CaTiO3)的結構。許多重要的介電晶體，例如: 鈦酸鋇(BaTiO3)、鋯酸鉛(PbZrO3)、鈮酸鋰(LiNbO3)、鉭酸鋰(LiTaO3)等都屬于此類型結構。

鈦酸鋇的晶胞如圖19所示，在立方體的頂角上是鋇(Ba)，鈦(Ti)位于體心，面心上是三組氧(O)。三組氧(OI，OII，OIII)周圍的情況各不相同，整個晶格是由Ba、Ti和OI、OII、OIII各自組成的簡單立方結構子晶格(共5個)套構而成的鈣鐵礦結構。

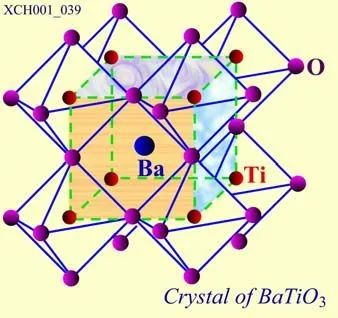
圖19 鈦酸鋇的晶胞

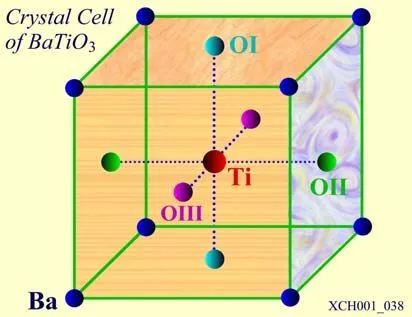
圖20 Ti的氧八面體排列

如圖20所示，如果把OI、OII、OIII連結起來，它們構成一個等邊三角形，整個原胞共有8個這樣的三角形面，圍成一個八面體，整個結構可看作為氧八面體的排列，鋇(Ba)在8個氧八面體的間隙里。鈣鐵礦型的化學式可寫為ABO3，其中A一般代表一價或二價的金屬，B代表四價或五價的金屬，且常把BO3稱為氧八面體基團。氧八面體是鈣鐵礦型晶體結構上的特點，它與這類晶體的一些重要物理性質有很大關系。實際上，許多具有亞鐵磁性的晶體(通稱鐵氧體)，也具有氧八面體結構，但不屬鈣鐵礦型。氧八面體結構和金剛石或閃鋅礦型中的正四面體結構是固體物理領域中非常受重視的兩大典型結構。

名詞解釋：

·原胞: 一個晶格中最小重復單元(體積最小)。

·基矢:原胞的邊矢量，三維格子的重復單元是平行六面體，基矢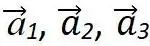?是重復單元的邊長矢量。在一些情況下，單胞就是原胞，而在一些情況下，單胞不是原胞，例如面心立方晶格。

·單胞(結晶學元胞): 為了反映晶格的對稱性，常取最小重復單元的幾倍作為重復單元。單胞的邊在晶軸方向，邊長等于該方向上的一個周期，代表單胞三個邊的矢量稱為單胞的基矢。

編輯：黃飛