近段來本人的簡易CNC控制器有小小突破,也基本上完工了,整理控制器資料時順手整理了"MACH3脈沖輸出",感覺還有兩篇沒有貼出就接著續篇(基本是按照自問自答的方式出現).....

圖片資料可以說是比效珍貴的,請珍惜(最少本人是這么認為的,因為這是MACH3實際輸出的波形,并無半點人工干涉,真正想返原它成圖并非是一件易事)

上幾單元說過了,MACH3控制步進電機是按脈沖方向來完成的,但實際上是怎一回事呢???

最常見的是G0 G1,而G0到底是怎走的呢?? 查閱G指令表: G0是點到點運動的,這在機器是如何運作的呢???

G0 測試

假如從A點到達B點情況是如何呢??

為此本人在通過自己寫的軟件進行分析MACH3波形實際輸出,從而清楚地解決了G0的實際運行方式:
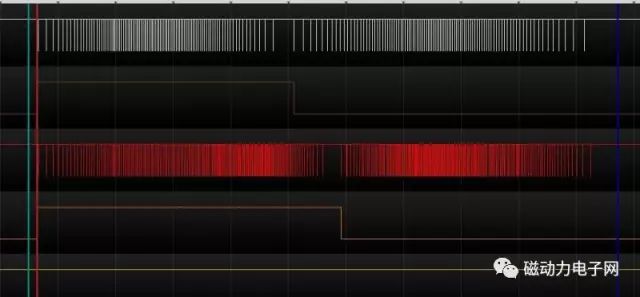
如圖所示(G0X1Y1)

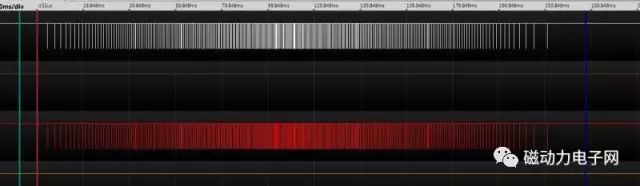
從這個波形來看,可以清楚地知道從A到B有三個過程,一加速過程,二均速過程,三減速過程,這三個過程中對XY來說是完全相同的,清認真看清下圖的直線,實際上并非是真正的直線,而是曲線,XY是你一步我一步.你走,我走,你走,我再走,從而在失量合成時就成了一條與X坐標系成45度角的類直線實際效果如圖

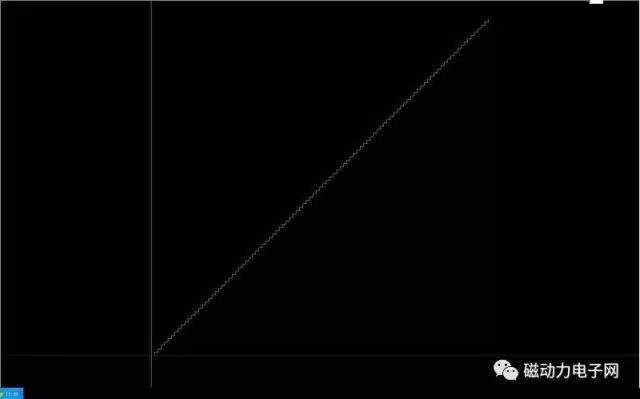
從圖中可能清楚地反應:速度從零開始,最后以零結速,加減速度過程并沒有改變直線的形狀,!!!

這個就是插補的奧妙了!!

有人會說這個簡單了,其實本人認為一點也不簡單,此過程中所包函的知識太多太多了,各位看官要是想了解更多找渡娘.

G1 測試

接著就是在CNC中起了結定性關鍵的G1了,

G1到底是什么一個過程呢? 測試兩個不同的圖形

{
G0x0y0
g1x1y1f1200
g1x1y2
x0y0
}

{
G0x0y0
g1x0y2f1200
x2y2
x0y0
}

直接看圖

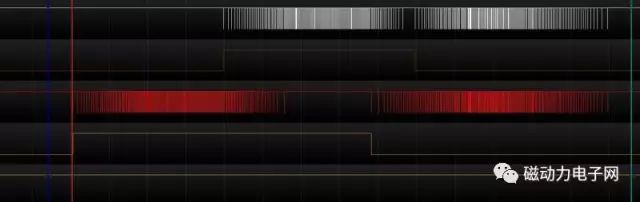
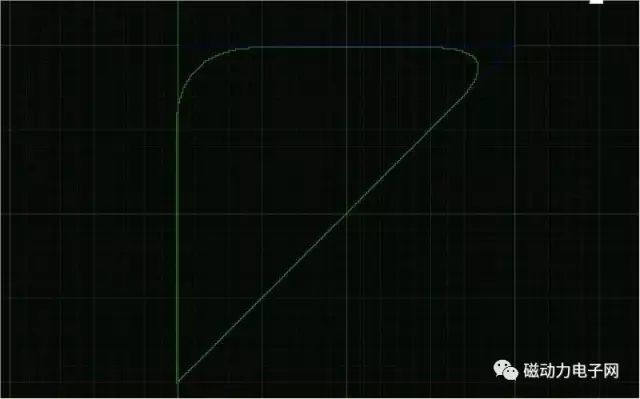
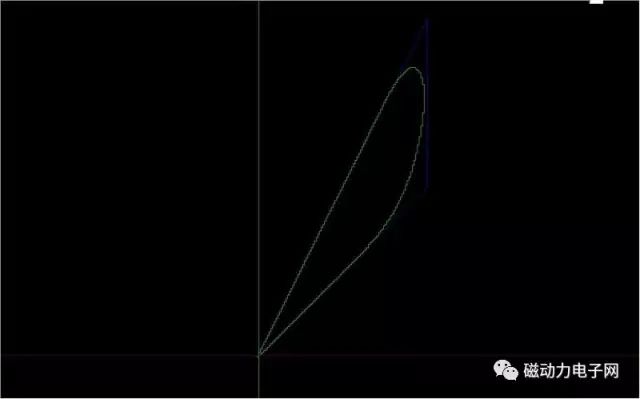
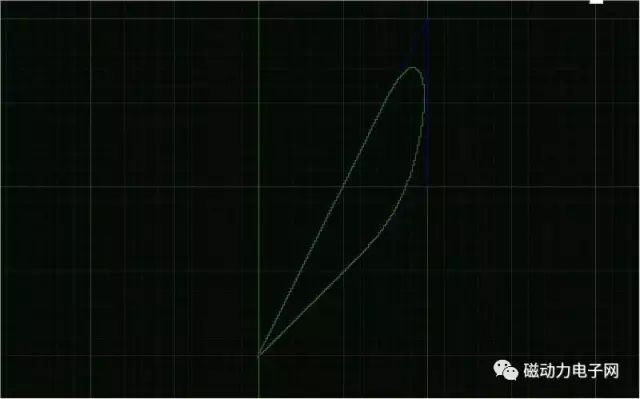
好奇怪的圖形啊,為什么會拐彎呢?? 是誰偷了我的銳角呢??

其實一點也不奇怪,因為有牛頓的慣性定侓存在一切物體運動都不能突變,對此MACH3做了一個非常強的拐角過程,以前有網友問過,為什么我的MACH3會出現圓角呢?這個就是給予最好的解答了.

而這個過程是衡量一個CNC好壞的一個關健.為什么會拐得這么漂亮呢?這個拐角方程式又是什么呢? 對于多軸多微線段中,此拐角還可以這么順嗎??此精度又會是多少呢?? 對此本人花了整整二年時間去解讀它,也算是有的小成!!

在眾多的文獻中,很多地方提到插補,而插補的本質是什么? 插補簡單來說: 根據給定的數學函數，在理想的軌跡式輪廓上的已知點之間，確定一些中間點的一種方法。直線插補這是車床上常用的一種插補方式，在此方式中，兩點間的插補沿著直線的點群來逼近，沿此直線控制刀具的運動。

注意兩個字"逼近" 為因為計算機并口輸出是脈沖方式,再者步進電機按每步進位一定的距離運行的,所以最后所得到的是一個非標準直線.只能逼近它.

脫離MACH3,假如我們用單片機或自己做的并口輸控制,我們有沒有方法去實現這個過程呢? 找渡娘后,所知有一種方式比較直接也比較有效那就是"比較法" 如下

直線插補就是零件程序提供直線段的起點、終點坐標,數控裝置將這兩點之間的空間進行數據密化,用一個個輸出脈沖把空間填補起來,從而形成要求的直線軌跡。

(一).偏差計算公式

直線方程 : yi/xi = ye/xe ; 把標準方程變換一下 xeyi - xiye = 0 ,令 實際偏差值是FI 側實際偏差值 FI = xeyi-xiye

進給方向的選取：使誤差減小的方向

當P點在直線上方時；

則：Xeyi － xiYe>0

當P點在直線下方時；

則：Xeyi － xiYe<0

因此：

由F可判別動點P與理想軌跡的相對位置，從而決定下一步移動方向。

F>0，點P在直線上方，應向+X 移動。

F<0，點P在直線下方，應向+Y 移動。

F=0，點P在直線上，為方便，將 F=0 歸F>0。

為便于計算機編程計算,將F的計算予以簡化。

設第I象限中動點P(xi, yi)的F值為Fi， Fi＝Xeyi-xiYe

1.若沿+x向走一步，即

于是有 Fi+1 = Fi -Ye

2.若沿+y向走一步，即

于是有：Fi+1 = Fi +Xe

(二)終點判別的方法有兩種：

1.每走一步，判斷動點P(xi, yi)的坐標值是否與終點坐標相同，即

Xi-Xe =0且 Yi-Ye=0

若兩式同時滿足，插補結束。

2.求程序段總步數n=Xe+Ye，每走一步，n-1->n，直到 n=0，插補結束。

知道方法,那程序如何編寫呢?? 假如運行至(4,3)坐標:

#include "XXOO.h" //頭文件(XXOO笑吧)
void main()
{ int xe,ye,f,j;
xe=4; ye=3; //把常數4寫入變量xe；把常數3寫入變量ye；
f=0; //把常數0寫入f；
j=xe+ye; //讀出xe和ye的值，相加后結果寫入j；
do {if (f>=0)
{if(ye>=xe) //判斷直線是否大于45度；
{cout<<"同時走+x，+y"< f=f+xe-ye; //讀出f、xe和ye的值，計算后結果寫入f；
j=j-2;} //讀出j的值，減2后結果寫入j；
else{cout<<"向+x走一步"< f=f-ye; j=j-1;}}
else {if (ye>xe)
{cout<<"向+y走一步"< f=f+xe; j=j-1;}
else {cout<<"同時走+x，+y"< f=f+xe-ye; j=j-2;}}}
while (j!=0);}

是不是很簡呢？實際這個是理論上的.而真正的運行是比這個復雜得多得多!!!!!!

此方法中只考慮到象限一,能不能用到四個象限之中呢??

對于第二象限，只要去| x |代替x即可，至于輸出驅動，應使x軸步進電機方向旋轉，而y軸步進電機仍為正向旋轉。

同理，第三、四象限的直線也可以變換到第一象限。插補運算時，取| x |和| y |代替x、y。輸出驅動原則是：在第三象限，點在直線上方，向-y方向步進；點在直線下方，想-x方向步進。在第四象限，點在直線上方，想-y方向步進；點在直線下方，想+x方向步進。4個象限各軸插補運動方向如上圖所示。由圖中看出，F>=0時，都是在x方向步進，不管+x向還是-x向，| x |增大。走+x或-x可由象限標志控制，第一、第四象限走+x，第二、三象限走-x。同樣，F<0時，總是走y方向，不論-y向還是+y向，| y |增大。走+y或-y由象限標志控制，第一、二象限走+y，第三、四象限走-y。

假如再加兩軸Z+Z-,A+A-,那么問題就大條了.所考慮到的就不是簡簡單單的比較了,更別說加上速度限定了.

看來"比較法"只能算是初等的算法了,有沒有更加高明的手段或算法呢?