1. 說在前面的話
2. 歐拉角
3. 歐拉角與四元數關系
4. Matlabe 歐拉角轉四元數
5.C語言實現歐拉角轉四元數
6. 獲取資源
1. 說在前面的話
1)在介紹以下內容之前,我們假設讀者已經對復數與2D旋轉、3D空間中的旋轉、四元數的性質以及四元數與3D旋轉等數學理論有一定的閱讀理解基礎。
2)歐拉角與四元數姿態表示方法是目前工程上最常用的兩種方法。歐拉角表示法具有簡便、幾何意義明顯等優點,同時姿態敏感器可以直接測出這些參數,能較方便地求解用這些姿態參數描述的姿態動力學方程。但采用歐拉角的姿態描述方法存在奇點問題,且需多次三角運算。而采用四元數表示方法則可以避免這些問題,因此目前工程上開始采用四元數來描述飛行器運動及動力學方程中的姿態,而在設計控制規律時,由于歐拉角的直觀性和幾何意義,仍然采用歐拉角描述。
2. 歐拉角
根據歐拉定理,剛體繞固定點的位移也可以是繞該點的若干次有限轉動的合成。在歐拉轉動中,將載體坐標系轉動三次得到導航坐標系。在三次轉動中,每次的旋轉軸是被轉動坐標系的某一坐標軸,每次的轉動角即為歐拉角。因此,用歐拉角確定的姿態矩陣是三次坐標轉換矩陣的乘積。
最終的姿態矩陣還與三次轉動的順序有關,下面公式采用3-2-1順序,即按照Z-Y-X軸的順序旋轉(東北地坐標系(對應的載體坐標系前右下)):
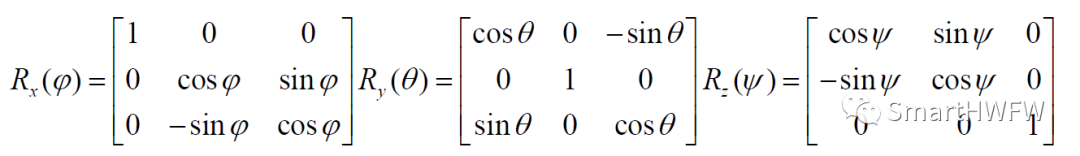
于是可得姿態矩陣
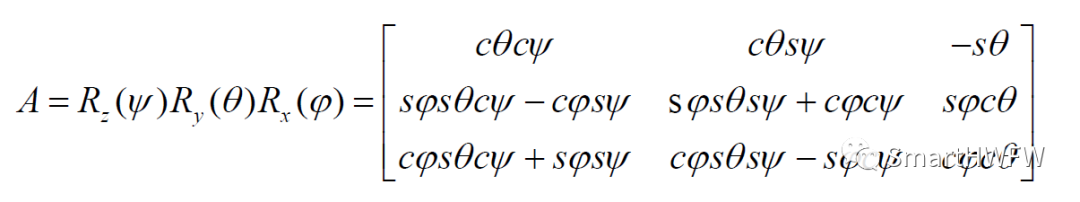
式中,字符"c","s"分別為"cos"和"sin"的縮寫形式。
3. 歐拉角與四元數關系
根據四元數的定義,可以將歐拉角式轉換為四元數,以歐拉3-2-1轉動為例:第一次先繞Z軸轉動,φ = θ =0,
四元數表示為:
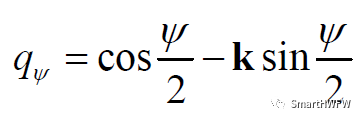
第二次先繞Y軸轉動,φ = ψ = 0,
四元數表示為:
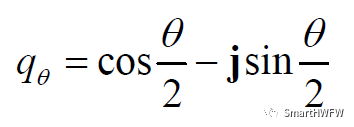
第三次先繞X軸轉動,θ = ψ = 0,
四元數表示為:
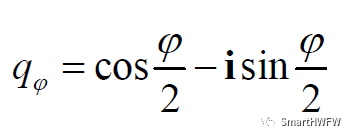
則,繞三軸轉動的合成為
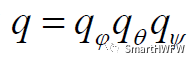
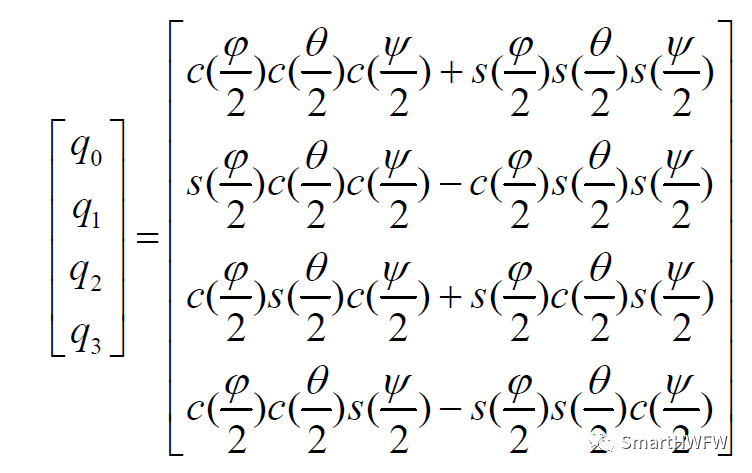
該轉換方法在360±°內均有效,是一對一的關系。
4. MATLAB 歐拉角轉四元數
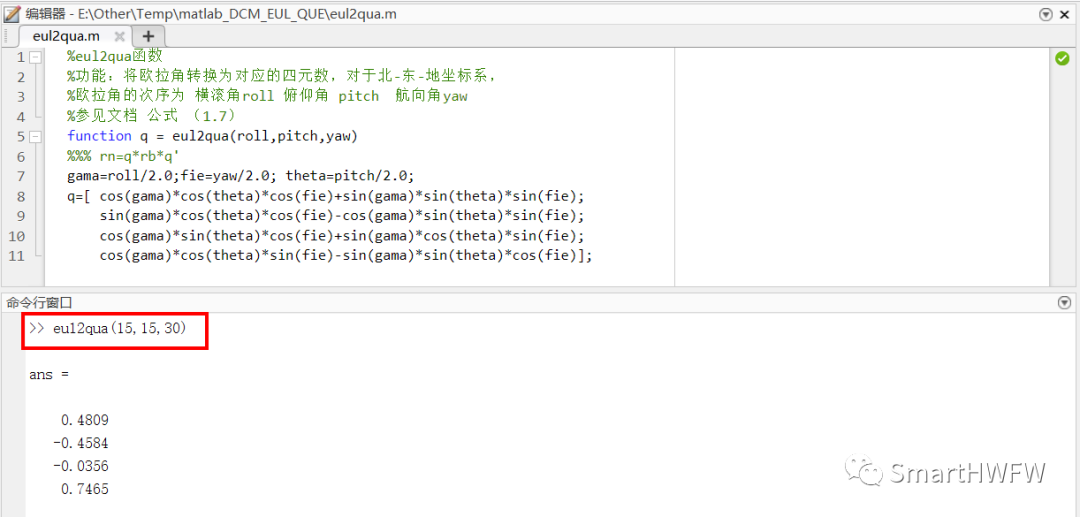
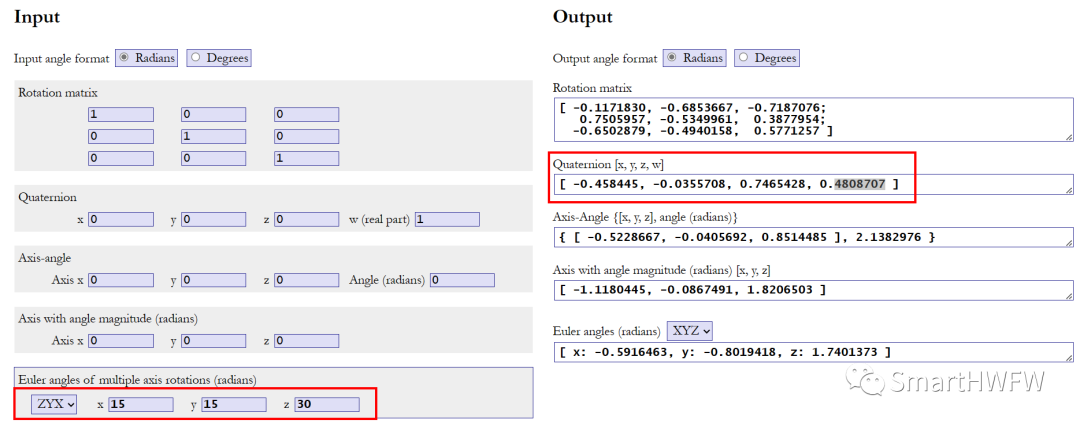
5. C語言實現歐拉角轉四元數
歐拉角轉四元數的步驟如下:
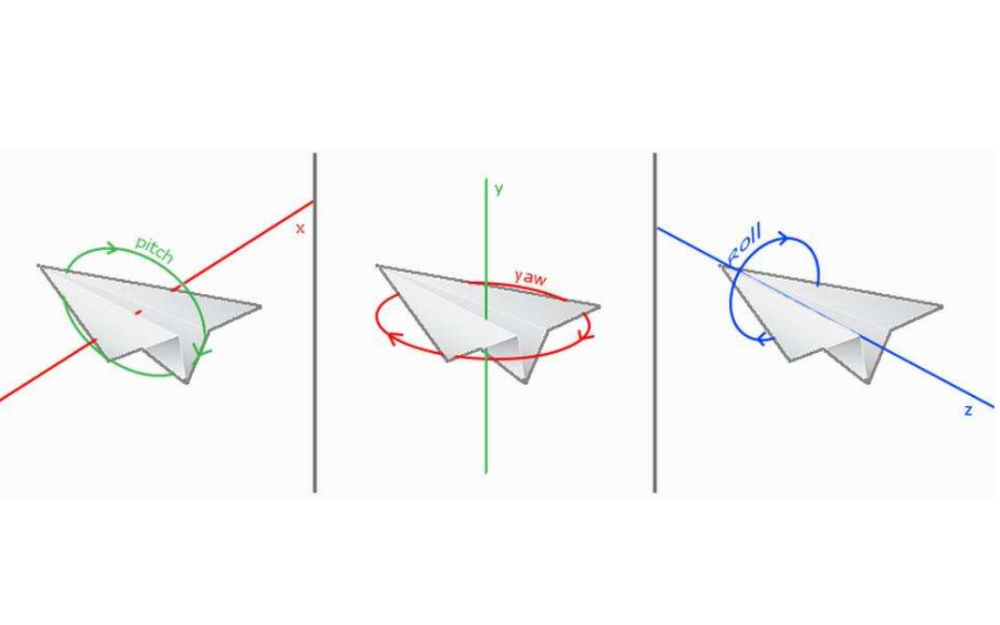
STEP1:確定每個歐拉角的軸和旋轉角度。Yaw對應y軸,Pitch對應x軸,Roll對應z軸。記為yaw_angle,pitch_angle和roll_angle。
STEP2:分別根據每個歐拉角的旋轉軸和旋轉角度,構造旋轉四元數的各個分量。以yaw_angle為例,qw = cos(yaw_angle/2)qx = 0qy = sin(yaw_angle/2)qz = 0
同樣地,根據pitch_angle和roll_angle可以得到對應的旋轉四元數分量。
STEP3:根據旋轉四元數的分量,構造最終的旋轉四元數。旋轉四元數的分量為(qw, qx, qy, qz)。
請注意,歐拉角到四元數的轉換是一個多對一的映射,即不同的歐拉角可能對應相同的旋轉四元數。因此,在實際應用中,可能需要根據具體需求選擇適合的歐拉角表示方式。
校驗結果:
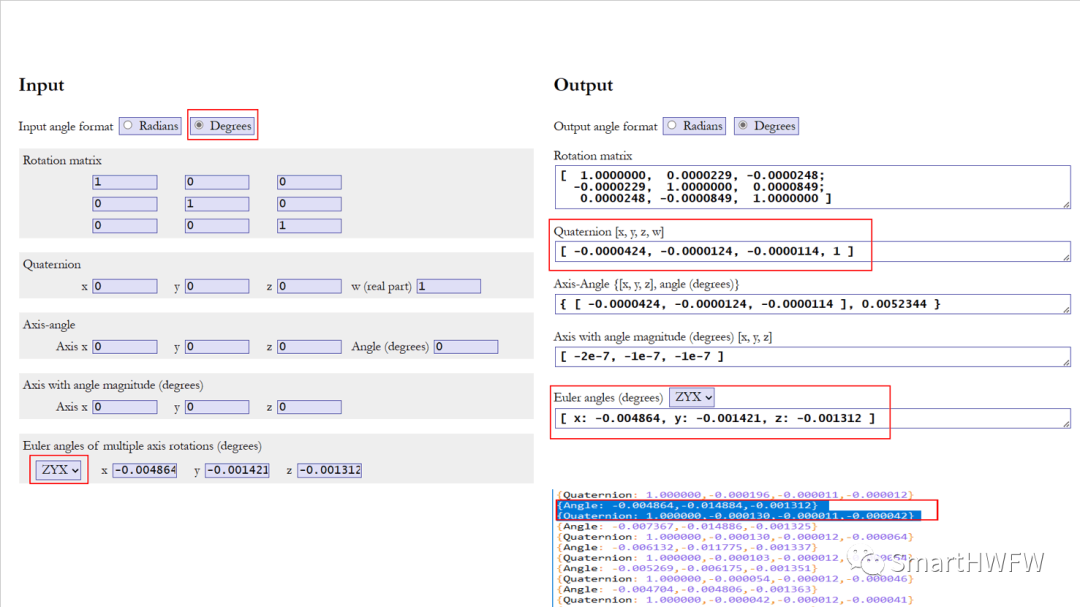
-
matlab
+關注
關注
182文章
2963瀏覽量
230199 -
C語言
+關注
關注
180文章
7601瀏覽量
136251 -
飛行器
+關注
關注
13文章
718瀏覽量
45472 -
歐拉角
+關注
關注
0文章
5瀏覽量
6763
原文標題:MEMS_慣性傳感器程序集02-歐拉角轉四元數
文章出處:【微信號:SmartHWFW,微信公眾號:SmartHWFW】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 C語言實現歐拉角轉四元數
C語言實現歐拉角轉四元數













評論