臨界導通模式(critical conduction mode,CRM)下的DC-DC變換器能夠降低系統階數,并且可以實現更高的效率而廣泛應用于中小功率場景中 ^[1-3^ ^]^ .為了提高非同步boost轉換器在CRM模式下的效率,一般考慮兩種功耗來源,即導通損耗和開關損耗 ^[4-5^ ^]^ .導通損耗通過選用更低的導通阻抗的元器件來降低,而降低開關損耗則須要讓開關在開啟瞬間兩端的電壓最低來實現軟開關 ^[6]^ .在boost轉換器中,一般而言使用谷值開關(valley switching,VS)和零電壓開關(zero-voltage switching,ZVS)來提高整體效率.
對于非同步拓撲,通常利用電感電流降到零后二極管的結電容Cj和MOSFET的輸出電容Coss與電路電感的諧振,實現主開關管的VS/ZVS ^[7-8^ ^]^ .這兩個電容均屬于寄生電容,表現出對電壓的強烈非線性關系.一般而言,普通硅基半導體寄生電容的非線性隨電路狀態(如溫度、開關頻率等)不同變化很大.相比之下,第三代半導體如基于氮化鎵、碳化硅的半導體,因其寬禁帶的特點,自身的各種特性對溫度不敏感 ^[9-11^ ^]^ .這個特性為碳化硅(SiC)二極管結電容Cj以及氮化鎵(GaN HEMT)輸出電容Coss在實際工程中奠定了良好的應用基礎.然而,開關元件參與諧振的寄生電容表現出對電壓的強烈非線性,這讓諧振過程難以直觀地理解并計算.文獻[12]為了簡化該諧振過程,將寄生電容視為恒定的值.文獻[13]將電容根據電壓等級分為兩段,方便了整體計算.文獻[14]盡管考慮了不同的間隔來計算近似諧振時間,但是并未給出諧振特性的具體解釋.這些文獻沒有給出足夠精確的諧振特性,因而與實際諧振過程存在一定誤差.
本研究通過對寄生電容的合理分段,提出了一個針對諧振情況下的分段等效電容模型,并基于此計算出了最優的VS/ZVS時間,根據此通過實驗結果的對比充分證明了模型的有效性及計算時間的準確性.
1 適用于Boost電路VS/ZVS實現的等效電路分析
為了減小開關管的開通損耗,電路須要實現VS或者ZVS.在非同步整流的boost電路中,實現該功能是利用開關管的輸出電容Coss 、二極管的結電容Cj與電路電感的諧振,適當設置MOSFET開通前的死區,讓其開通瞬間兩端電壓最小.
圖1所示為基于GaN的boost電路基本拓撲,圖中:vin為輸入電壓;vo為輸出電壓;L為電路電感;Q為主開關管;D為二極管;C為電路輸出電容;R為負載;iL為電感電流;vgs為開關管驅動電壓;vds為開關管兩端電壓;vr為二極管兩端電壓;Coss為主開關管的寄生電容;Cj為二極管的寄生電容.
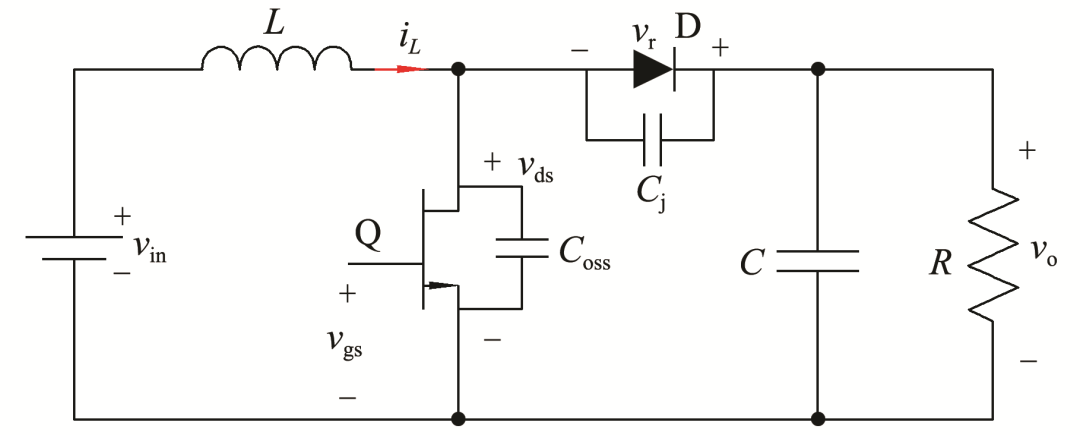
圖1 基于GaN HENT的boost電路基本拓撲
由于VS情況可以看做ZVS情況下的延伸,因此下面以ZVS情況為例進行分析.圖2所示為ZVS情況下boost電路在CRM模式下的電壓電流波形,圖中:Ton為主開關管開啟時間;Toff為主開關管斷開時間;tf為電感電流的下降時間.詳細過程以時間段分開討論.
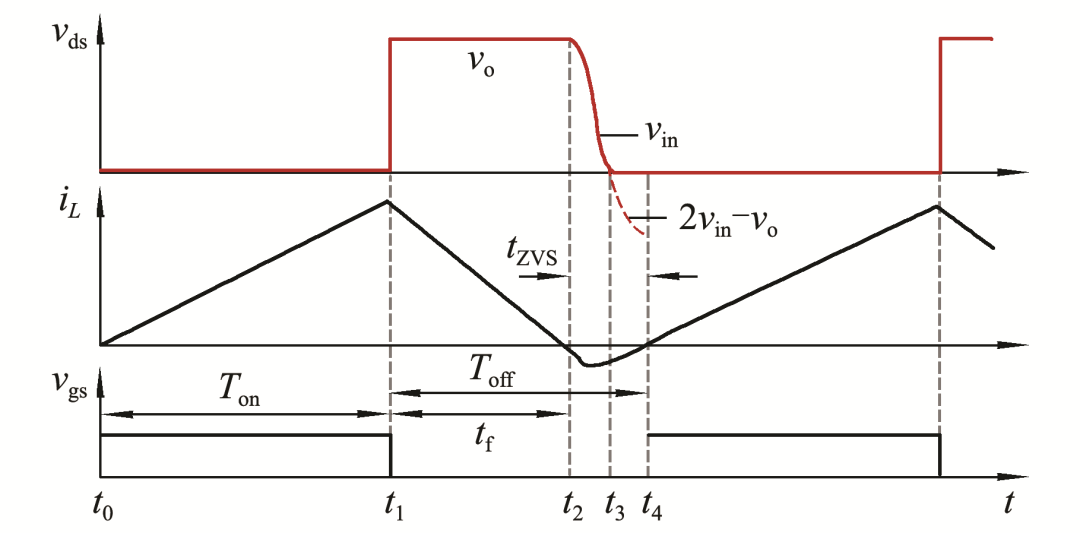
圖2 boost電路在CRM模式下的電壓電流波形
[t0 ,t1 )時間段:周期在t0時刻開始,開關管開啟,vds =0,vr =vo ,電感電流在t0時刻從0開始上升.
[t1 ,t2 )時間段:t1時刻開關管關閉,vds =vo ,vr =0,電感電流在t2時刻下降至0.
[t2 ,t3 )時間段:二極管和主開關管均處于斷開狀態,Coss和Cj開始參與諧振.如圖2所示ZVS情況下,t3時刻vds諧振值至0,iL諧振值未到0,但諧振過程結束.而VS情況作為ZVS的一種延伸情況,在t3時刻vds諧振值至最低點,iL諧振值至0,周期結束.
[t3 ,t4 ]時間段:針對零電壓情況,主開關管反向導通,iL以 L /vin的速率在t4時刻上升至0,周期結束.
在以上的分析中,對于VS情況,考慮諧振過程最低點即可得到tvs的時間;對于ZVS情況,tzvs由諧振過程及電流回零過程組成,其中兩者共同須要考慮的是諧振過程.
由于在實現VS/ZVS過程中電路的輸出電容遠大于兩個寄生電容,因此該諧振過程基本拓撲可以等效為圖3所示的諧振電路.
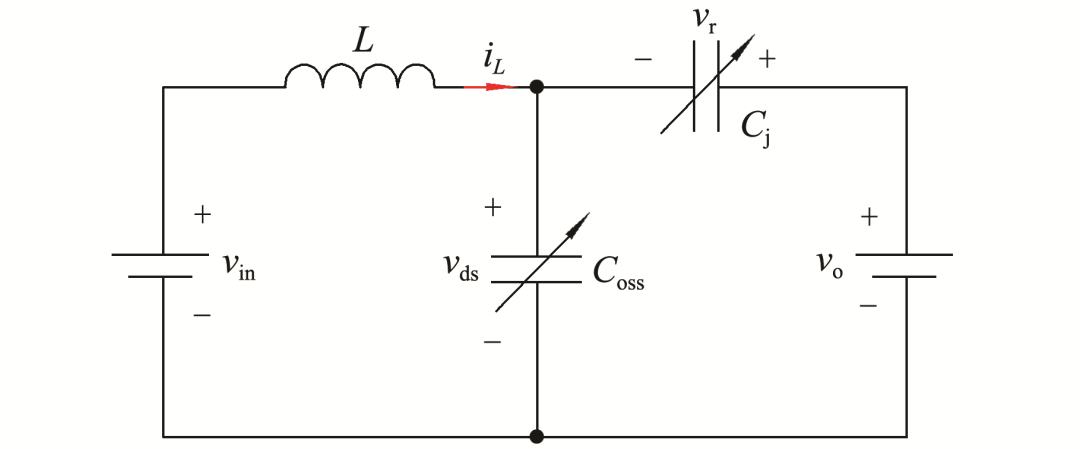
圖3 實現VS/ZVS過程中的等效諧振電路
以t2時刻為起始時間點給出節點的電壓電流微分方程為:
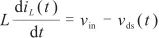 ; (1)
; (1)
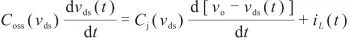 . (2)
. (2)
可以得到如下微分方程組
|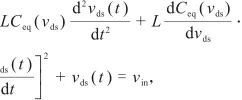 (3)
(3)
式中Ceq (vds ) C
Coss (vds )+Cj (vds ),其中Coss ,Cj與vds是強烈非線性關系,因此可以視為vds的函數.顯然,式(3)是一個二階非線性微分方程,其解析解很難求得.然而觀察到:當左邊第二項系數dCeq (vds )/dvds為零時,式(3)即可看做二階線性微分方程,能夠求得解析解.
以該方程為基礎,本研究提出一種針對非線性電容的分段電容模型,基于該模型導出上述諧振過程的解析解,并求得實現boost電路CRM模式的最優VS/ZVS時間.
2 非線性電容的分段等效模型及VS/ZVS時間的求解
根據對式(3)所示的非線性微分方程的線性化,首先提出一種針對Coss和Cj在諧振過程中的分段等效電容模型,然后依據該模型給出計算諧振過程的基本計算方法.
2.1 分段等效電容模型
分段等效電容模型的建立主要是將非線性電容根據不同電壓等級分段取等效恒定的值,以此建立分段等效電容模型.以vo 400 V為例,圖4所示為適用于諧振狀態下的分段等效電容模型示例.圖 4(a)為C
400 V為例,圖4所示為適用于諧振狀態下的分段等效電容模型示例.圖 4(a)為Coss及其分段等效值,其中:v5 =0 V,v1 =400 V,v4和v3為分段的電壓邊界;Coss,1 ,Coss,2和Coss,3為Coss被分段后每一段的等效值.圖4(b)為Cj及其分段等效值,其中:v1 =400 V,v2為分段的電壓邊界;Cj,1和Cj,2為Cj被分段后每一段的等效值.
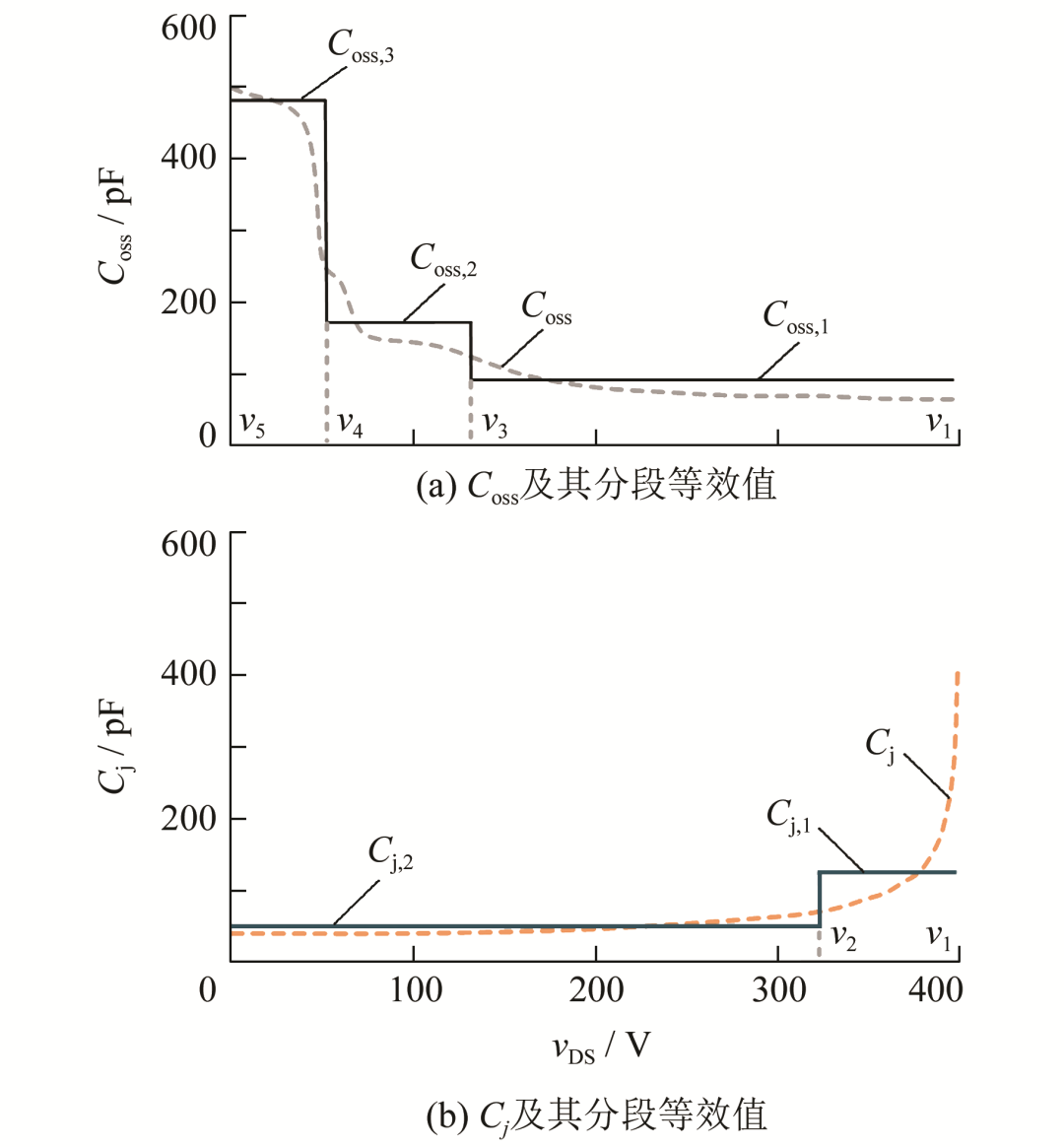
圖4 當 v =400 V時適用于諧振狀態下的分段等效電容模型
由圖4可知:Coss被分為了三段,其中每一段的邊界電壓值v4和v3的選擇讓邊界上的電容值滿足Coss ( vn+1 )=2Coss ( vn ) ( n =3,4).相比較而言,當二極管兩端的電壓變高時,諧振后Cj (vds )迅速下降至較小值.由于在大多數情況下Cj比Coss小得多,因此可以將Cj (vds )分為兩段,其中邊界條件滿足Cj (v2 )=2Cj (v5 ).
根據Ceq (vds )=Coss (vds )+Cj (vds ),將Coss與Cj的分段等效值疊加在一起,即可以得到一組不同電壓范圍下的等效電容值列表,如表1所示.
表1 不同電壓范圍下的等效電容值

2.2 分段電容值
根據分段等效電容模型建立的方式,為了計算諧振過程的解析解,通過基于電荷的等效方法獲得每個間隔的等效電容,即計算每個間隔的平均電容.
對于邊界電壓為va和vb的區間,等效電容上的電荷QC滿足
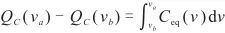 . (4)
. (4)
由于每個區間求得的電容值是一個常數,因此該區間的等效電容值為
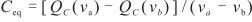 . (5)
. (5)
根據式(5)所示的計算方法得到每一段的等效電容值.
2.3 諧振過程的解析解及最優VS/ZVS時間
根據等效電容模型及其各個區間的初始條件得出諧振過程中vds和iL的解析解.下面首先描述解析解的求解方法,然后依據求得的解析解得到最優VS/ZVS時間.
為了更清晰地描述求解過程,將諧振過程依據電容等效模型的區間重新示意,如圖5所示.其中諧振初始點在t1時刻,對應電壓值v1 ,4個電容值區間的時間邊界依次為t2 ,t3和t4 ,分別對應邊界電壓v2 ,v3和v4 .電壓值在tzvs1時刻到0 V,電感電流在tzvs2時刻上升至0 A,為ZVS的最佳時間點.

圖5 在ZVS情況下vds和iL的諧振波形
雖然電容值隨電壓變化,但是諧振結構在諧振期間保持不變,經過分段等效后電路的諧振結構保持不變,且依舊滿足式(3).因為每一段的電容值是一個定值,所以非線性微分方程(3)可以轉化為
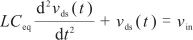 . (6)
. (6)
顯然,式(6)是一個二階線性微分方程,當vds >0時其通解為
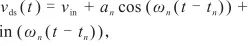 (7)
(7)
式中 (n
(n 1,2,3,4).將式(7)代入式(2)得到電流在諧振過程中的解析式為
1,2,3,4).將式(7)代入式(2)得到電流在諧振過程中的解析式為
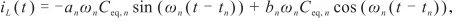 (8)
(8)
式中an和bn為常數,須要通過求解邊界條件來確定,對于式(7),設t t
tn即可得到 ,b
,bn的求解則須要通過電流的邊界條件給出.類似地,設t t
tn并對式(7)求時間t的微分,得到dvds ( tn )/dt b
bnωn ,則bn可以求得為
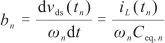 .
.
根據諧振過程中電壓的解析式,可以通過迭代求得實現VS的時間點或實現ZVS的初始點tzvs1 .此后,電感電流將以vin /L的斜率上升到零,此時GaN HEMT反向導通,因此可得出最佳ZVS點即電感電流過零點tZVS2為
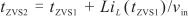 .
.
3 仿真和實驗結果
為了驗證非線性電容分段等效模型在計算VS/ZVS時間的時候的有效性,設計了一個輸入電壓范圍為90240 V、輸出電壓為400 V、電感大小為54 μH、輸出功率為200 W的CRM boost變換器.電路采用型號為GS66508T的GaN HEMT主開關管,型號為STPSC8H065的SiC主二極管,電路輸出電容為2 μF,開關頻率為250450 kHz.以下仿真數據基于實驗所用器件的數據表.
3.1 仿真結果
圖6(a)所示為基于分段等效模型tvs ,tzvs1和tzvs2隨輸入電壓vin變化的曲線計算結果,其中輸入電壓vin的范圍為90240 V.可以看到:tvs和tzvs2所示的曲面連續且光滑,說明計算結果符合邏輯規律.由于ZVS情況下電壓第一次到0 V所需要的時間會減小,因此可以看到圖中tzvs1~ <tzvs2一直成立.圖6(b)所示為基于恒定電容模型的計算結果,可以看到結果與分段等效模型的結果相差較大,下面通過實驗來驗證.
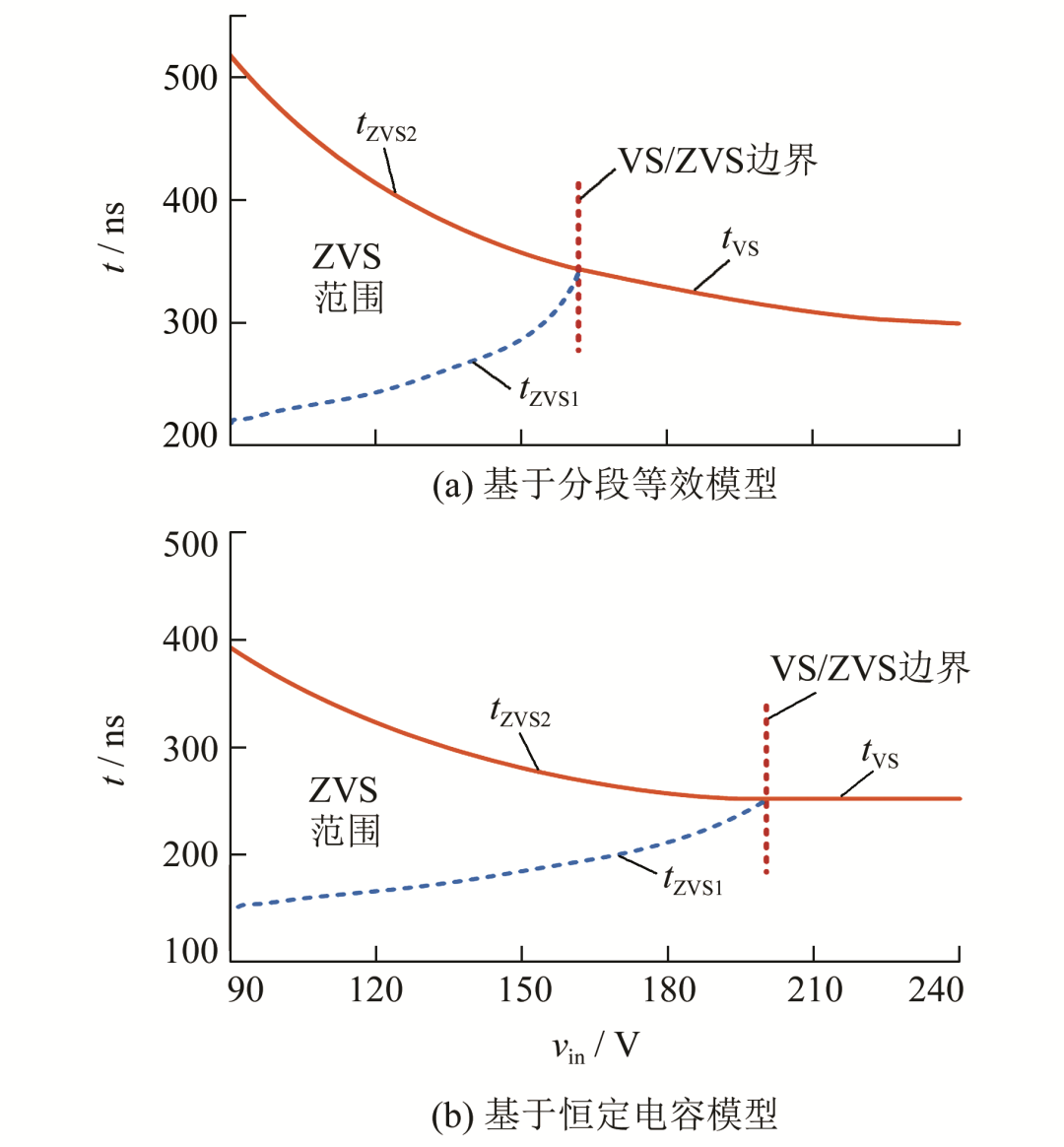
圖6 隨輸入電壓變化的VS/ZVS時間曲線
3.2 實驗結果
分別在boost電路實現VS,ZVS及VS/ZVS邊界的情況下驗證基于分段等效電容模型計算得到的tvz /tzvs .
圖7所示為CRM模式下boost電路中主要電壓電流波形,由示波器存取波形數據繪制.圖7(a)為實現VS時的電壓電流波形,根據電流的過零點確定電壓的谷值點,其中vin =200 V,tvs =320 ns,圖6中相同條件下基于分段等效電容模型的時間為315 ns,誤差為5 ns,相同條件下基于恒定電容模型的時間為252 ns,誤差為68 ns;圖7(b)為VS與ZVS邊界時的電壓電流波形,根據電流的過零點確定電壓的谷值點,其中vin =165 V,tzvs =340 ns,圖6中相同條件下基于分段等效電容模型的時間為342 ns,誤差為2 ns,相同條件下基于恒定電容模型的時間為271 ns,誤差為69 ns;圖7(c)為實現ZVS時的電壓電流波形,根據電流的過零點確定電壓的谷值點,其中vin =135 V,tzvs =375 ns,圖6中相同條件下基于分段等效電容模型的時間為380 ns,誤差為5 ns,相同條件下基于恒定電容模型的時間為303 ns,誤差為72 ns.
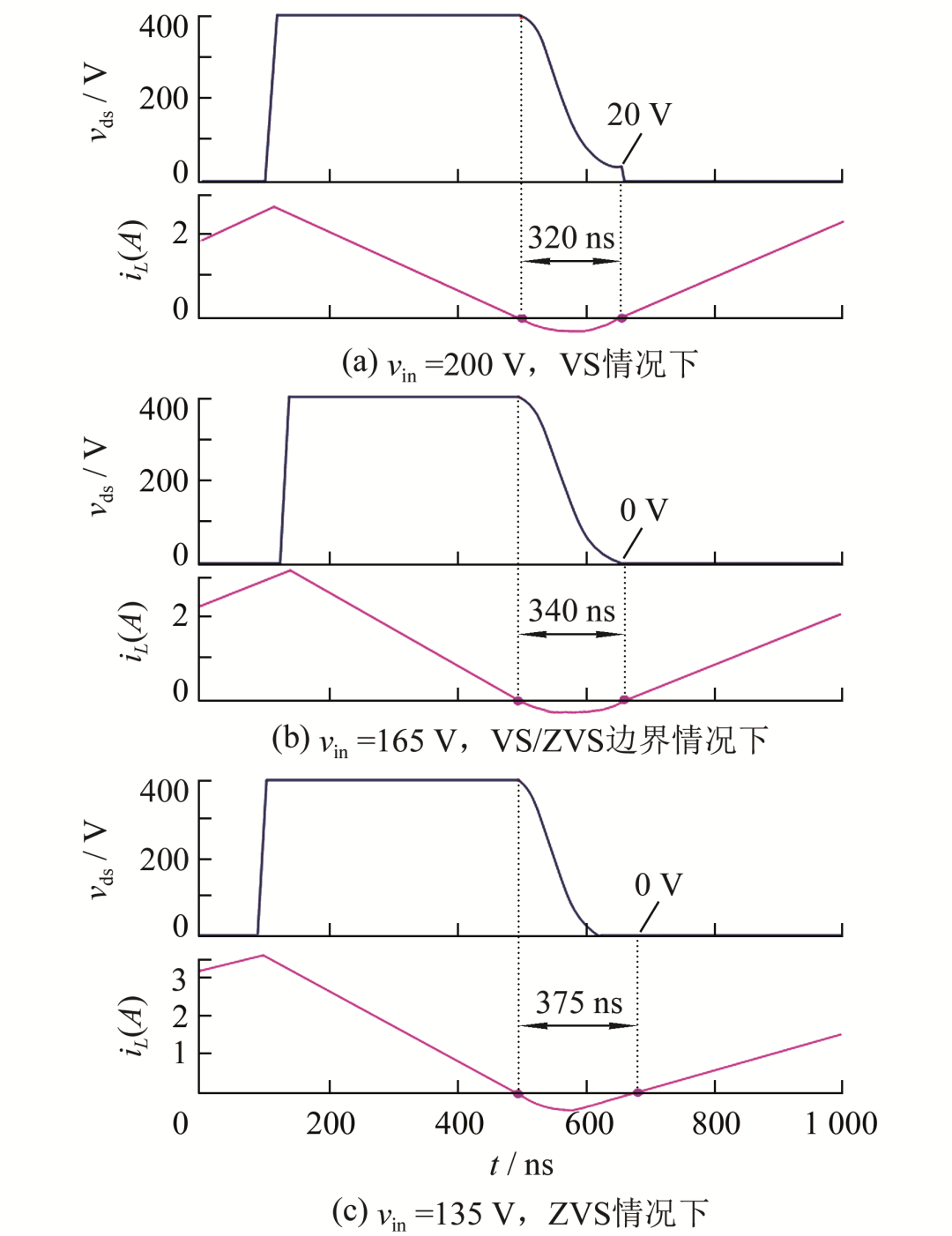
圖7 CRM模式下boost電路中主要電壓電流波形
以上實驗中實現VS和ZVS的諧振時間與模型計算時間誤差不超過5 ns,表明了模型及其計算結果的有效性.實驗結果表明:利用所提出的分段等效電容模型計算的VS/ZVS時間足夠準確,為實際VS和ZVS的實現提供了指導性的方法,并且為電力電子領域其他須要考慮非線性場合的計算提供了解決思路.
-
二極管
+關注
關注
147文章
9574瀏覽量
165897 -
MOSFET
+關注
關注
144文章
7088瀏覽量
212721 -
寄生電容
+關注
關注
1文章
291瀏覽量
19192 -
boost電路
+關注
關注
3文章
164瀏覽量
30283 -
DC-DC變換器
+關注
關注
6文章
85瀏覽量
15321
發布評論請先 登錄
相關推薦
無源軟開關BUCK、BOOST電路的研究
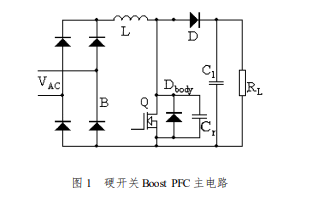
Boost PFC電路中開關器件的損耗分析與計算的詳細資料說明
晶體三極管的開關時間和測量
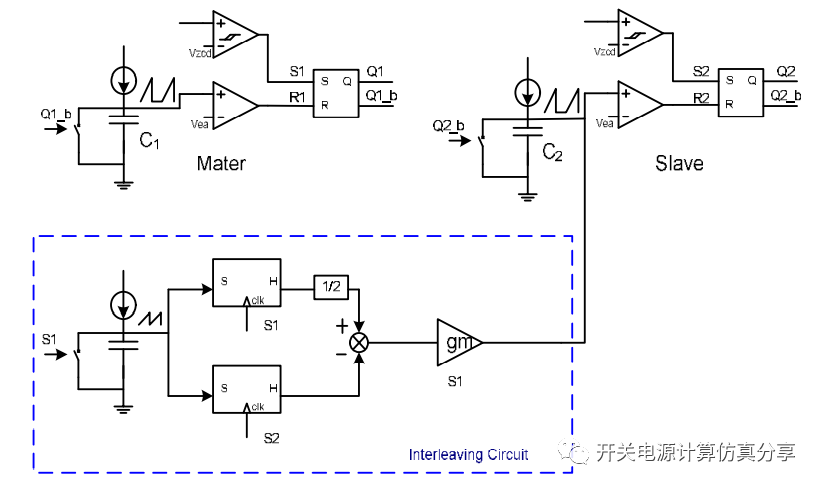
交錯CRM BOOST PFC仿真(1)




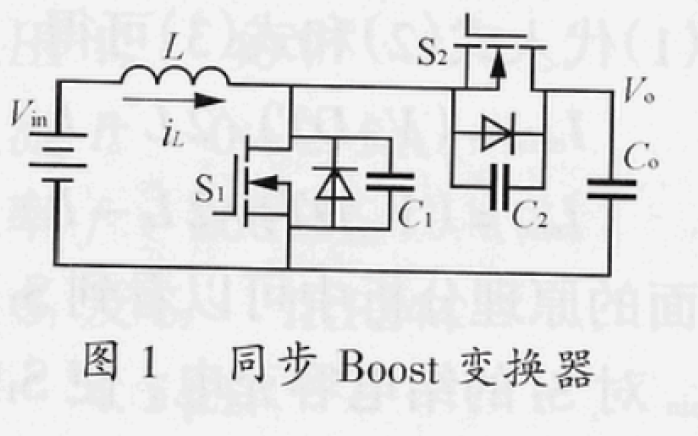
 基于分段模型的CRM boost電路軟開關時間優化設計
基于分段模型的CRM boost電路軟開關時間優化設計










評論