在計算傅里葉變換之前對信號去趨勢是一種常見的做法,特別是在處理時間序列時。在這篇文章中,我將從數學和視覺上展示信號去趨勢是如何影響傅里葉變換的。
這篇文章的目的是讓介紹理解什么是常數和線性去趨勢,為什么我們使用它們,以及它們是如何影響信號的傅里葉變換的。
傅里葉變換快速回顧
我們將使用傅里葉變換的如下定義:對于輸入序列x[n],當n=0到n時,傅里葉變換的第k個系數為以下復數:
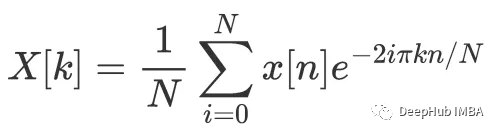
常量去趨勢
序列x[n]可以分解如下:將其寫成兩個信號的和:“常數部分”等于信號的平均值,“平均值周圍的可變性”部分給出實際信號與其平均值之間的差值:

對于所有樣本n,我們有:

首先,求x均值的傅里葉變換

這是一個簡單的序列,所以在k=0處x的均值為0,在其他地方的值也為0。

使用下面代碼繪制所有指數也可以看到為什么它們的和總是為0(除了k=0)。
import numpy as np
import matplotlib.pyplot as plt
N = 10
ns = np.arange(N)
fig, axes = plt.subplots(1, N//2+1, figsize=(18,8), sharex=True, sharey=True)
for k in range(0, N//2+1):
eiks = np.exp(-2*1J*np.pi*ns/N*k)
pretty_ax(axes[k])
plot_sum_vector(eiks, axes[k])
axes[k].set_title(f'k={k}')
axes[k].set_aspect('equal')
fig.suptitle(f'Complex plot of the $e^{{-2ipi kn/N}}$ families')

現在我們把x的傅里葉變換寫成這樣,分為兩部分

分解x的傅里葉變換,結果是2個傅里葉變換的和:“可變性”部分的傅里葉變換,以及k=0時等于平均值的系數。
也就是說x的傅里葉變換等于其可變性在均值附近的傅里葉變換的和,再加上除k = 0處之外的序列,這個序列都為0,所以他的均值是x。
這就常數去趨勢,是在進行傅里葉變換之前去除信號的均值。對于傅里葉系數,就傅里葉系數而言,它對應于將k = 0系數設置為0。
k = 0的系數始終等于信號的平均值,可以使用下面方法證明:

線性去趨勢
方法與前面相同:將輸入信號寫為2個部分的和:“線性”部分,以及圍繞該線性部分的其余變化:

這里的線性部分是從最小二乘擬合計算。利用指數,可以將線性部分寫為:

其中b是信號的平均值。讓我們來看看它的傅里葉變換:

線性部分的傅里葉變換為,給定傅里葉變換的線性性質:

線性去趨勢包括在進行傅里葉變換之前去除x的線性部分:它從結果中去除aFT(n)+b項,其中a是常數因子(對應于線性擬合的斜率),FT(n)是線性序列[0,1,…]的傅里葉變換,b是信號的平均值(因此第一個傅里葉系數將為0,就像常數去趨勢一樣)。
python代碼
在Python中使用numpy和scipy實現非常簡單。
Scipy在它的signal 包中提供了detrend函數,帶有一個類型參數來指定我們是想讓信號保持常量趨勢還是線性趨勢。
在下面的例子中,創建了一個長度為20個樣本的信號,其中包含一個前導系數為2的線性部分,一個噪聲,一個偏移量為4的正弦部分。
import numpy as np
from scipy.signal import detrend
import matplotlib.pyplot as plt
N = 20
# create a sample signal, with linear, offset, noise and sinus parts
ys = np.arange(N) * 2 + 4 + np.random.randn(N) + 4*np.sin(2*np.pi*np.arange(N)/5)
# constant and linear detrend
ys_c = detrend(ys, type='constant')
ys_l = detrend(ys, type='linear')
fig, axes = plt.subplots(1, 2)
ax = axes[0]
ax.plot(ys, label='raw')
ax.plot(ys_c, label='constant-detrended')
ax.plot(ys_l, label='linear-detrended')
ax.legend()
ax.set_title('Input signal')
ax = axes[1]
# we use rfft since our input signals are real
ax.plot(np.abs(np.fft.rfft(ys)))
ax.plot(np.abs(np.fft.rfft(ys_c)))
ax.plot(np.abs(np.fft.rfft(ys_l)))
ax.set_title('Module of Fourier-transform')

在左邊我們有原始輸入信號,以及它的常數去趨勢和線性去趨勢版本。
常數去趨勢有效地去除信號的平均值,使其在0附近居中。線性去趨勢不僅去掉了信號的平均值,而且還去掉了它的線性趨勢(又名“直線斜率”)。從視覺上看,在線性去趨勢信號上比在原始信號上更容易發現正弦部分。
右邊是每個信號的傅里葉變換模塊:如果不去除趨勢,我們得到藍色模塊。使用常數去趨勢法去除平均值可以有效地將0系數設置為0,這在大多數情況下使得圖表更容易分析。自線性去趨勢的結果是最好的:輸出傅里葉系數很好地顯示了輸出頻譜中的頻率,線性去趨勢的主要優點是它大大減少了頻譜泄漏。
線性信號的傅里葉變換
對于不同的K值,我們可以很容易地畫出線性信號Kn (K為斜率)的傅里葉變換:
import numpy as np
import matplotlib.pyplot as plt
N = 10
ns = np.arange(N)
Ks = [-5, 2, 5]
fig, axes = plt.subplots(len(Ks), N//2+1, figsize=(18,8), sharex=True, sharey=True, gridspec_kw={'hspace':0, 'wspace':0})
for i, K in enumerate(Ks):
xs = K*np.arange(N)
for k in range(0, N//2+1):
Zs = xs * np.exp(-2*1J*np.pi*ns/N*k) / N
ax = axes[i, k]
pretty_ax(ax)
plot_sum_vector(Zs, ax)
ax.set_aspect('equal')
ax.set_xlabel(f'k={k}')
axes[i, 0].set_ylabel(f'K={K}')
fig.tight_layout()

對于給定的k值,用紅色箭頭表示的傅里葉系數總是對齊的,并且等于一個比例。所以輸出頻譜中被去掉的部分總是序列[0,1,…N]的傅里葉變換的部分,其比例因子由線性擬合的斜率給出。
總結
在這篇文章中,我們介紹了常量和線性去趨勢:它們分別由去除輸入信號的平均值或線性擬合組成。在計算傅里葉變換之前的預處理步驟有助于使輸出譜更容易解釋。
去除信號的平均值使第0個系數為0。結果圖更容易檢查,因為大多數情況下,平均值與頻譜的其余部分相比可能相當大。如果我們去掉這個系數,y軸的尺度就更容易設定。
線性去趨勢除了去掉平均值也去掉了信號中的總體趨勢,這通常是原始信號的主導部分,這樣可以去掉其他成分例如季節行為等,所以如果需要對季節性進行分析還需要另外的處理。
-
信號處理器
+關注
關注
1文章
251瀏覽量
25252 -
最小二乘法
+關注
關注
0文章
22瀏覽量
8434 -
python
+關注
關注
56文章
4782瀏覽量
84451 -
頻譜儀
+關注
關注
7文章
339瀏覽量
35990 -
傅里葉變換
+關注
關注
6文章
437瀏覽量
42562
發布評論請先 登錄
相關推薦




 從數學和視覺上展示信號去趨勢是如何影響傅里葉變換的
從數學和視覺上展示信號去趨勢是如何影響傅里葉變換的










評論