P3P 問題是經典的多視圖幾何問題之一，其中標定的相機的絕對位姿由三個 2D-3D 對應關系決定。由于這是許多視覺系統的關鍵（例如定位和SfM），因此過去有很多研究關注于如何開發更快、更穩定的P3P算法。雖然當前SOTA的求解器既非常快又穩定，但仍然存在可能崩潰的配置。本文將問題代數化為尋找兩個圓錐的交點。通過這個方式，我們能夠分析表征多項式系統的實根，并為每個問題實例采用量身定制的解決方案。這導出了一個快速穩定的P3P求解器，它能夠正確解決其它方法可能會失敗的情況。實驗評估表明，該方法在速度和成功率方面都優于當前的SOTA方法。

1 什么是P3P問題

PnP是指根據2D-3D對應關系集合估計相機絕對位姿，集合最小的情況是P3P問題。P3P是將2D-3D對應關系通過相機內參轉換為3D-3D對應關系進行求解。給定世界坐標系中的3個3D點以及它們對應的歸一化圖像點，兩個點集通過剛體變換關聯：

其中是某個正數。P3P的目標是求解其中的旋轉和平移。

2 P3P問題發展史

P3P作為一個幾何問題歷史悠久，比計算機視覺領域的出現都要早很久。早在1773年Lagrange就在研究這個問題，Lagrange證明該問題最多可能有4個實數解，可以轉化為4次多項式問題求解。大約1個世紀后，1841年德國數學家Grunert重新研究了該問題，給出了一種直接求解方法。20世紀早期，該問題在攝影測量領域內受到關注，但主要關注點在于精調而不是從頭求解。Finstenvalder和Scheufele在1937年證明P3P問題只需要找到1個三次多項式的1個根和2個二次多項式的根。該問題后來在1981年Fischler和Bolles的RANSAC論文重新露面，由于RANSAC的成功，該問題也開始受到很大的關注。

根據最后需要求解的一元多項式的階次，P3P問題可分為兩大類：求解1個四次方程和求解1個三次方程。

最近的大多數工作關注于將P3P問題轉化為求解四次方程問題。Gao等人在2003年用吳零點分解法第一次給出了P3P的完成解析解。Kneip等人2011年提出了一種直接由計算相機絕對位置和旋轉的方式求解P3P問題的方法，避免了特征值分解或奇異值分解。Ke等人2017年提出用相應的幾何約束確定相機的旋轉。Banno和Nakano分別于2018和2019提出了P3P的直接求解法，通過估計中間坐標系中的距離，使得旋轉矩陣可以形式化為距離的線性表示。

與基于四次方程的方法不同，基于三次方程的方法在P3P問題的文獻中沒有得到太多關注。自Finstenvalder和Scheufele在1937年的工作以來，Grafarend等人在1989年也使用了三次方程，他們試圖將（3）簡化為齊次形式，然后使用與Finstenvalder和Scheufele相同的技術求解。Haralick等人在1991年回顧了P3P問題的主要基于三次方程的解法，并討論了數值精度。最近，Persson和Nordberg在2018年展示了關于尋找旋轉和平移的更多細節，并提出了一種使用三次方程的一個根的有效算法，該方法比以前的方法有更好的數值精度，并且更快。

3 P3P問題轉化為兩個圓錐曲線相交問題

參照Persson和Nordberg在2018年的解法，為了消除旋轉和平移參數，如圖1所示，有如下約束：

根據余弦定理，

其中。我們的目標是找到的解，從而求解旋轉和平移。我們可以假設，不然3D點就和相機中心一樣了。將(3)中前兩個式子除以第三個式子，并通過變量替換，可以得到以下二元二次方程組：

其中

現在問題變為求兩個二次方程的實數解，也就是說找到兩個圓錐曲線的實數交點。

4 本文的方法

本文的方法的基本思路也是求解兩個圓錐曲線的相交問題。(4)和(5)的兩個二次方程可以重寫為：

其中為的矩陣。為了找到交點，首先構造一個矩陣

交點可通過構建一個與真正的解相交的退化圓錐曲線找到。退化圓錐曲線由以下命題給出：

命題1（退化圓錐曲線，見《計算機視覺中的多視圖幾何》）如果矩陣 不滿秩，則圓錐曲線退化。退化點的圓錐曲線是兩條線(秩為2)或一條重復線(秩為1)，可以寫為：

其中。

退化圓錐曲線被構造出來后，可以被分解為（至多）兩條直線(和)，可以進一步很容易地與原來的兩個圓錐曲線相交。

4.1 尋找退化圓錐曲線

根據定理1，退化圓錐曲線需要非滿秩，即行列式為0：

得到關于的三次方程。求解(11)可以得到的值，并得到矩陣。注意原始方程組的任何解(同時屬于圓錐曲線)也在退化圓錐曲線上。

對于(11)中的每個解，都可以得到一個退化圓錐曲線。根據(10)，退化圓錐曲線是兩條直線和的組合。那么如何將退化圓錐曲線分解為兩條直線呢？

4.1.1 方法一：直接求解直線

這里展示一種尋找直線的直接方法。假定已經找到了一個退化圓錐曲線，寫為如下形式：

由于，假設，矩陣也可以寫為：

假定，令，則

根據(14)和(15)可以解出, 進而根據(16)和(17)可求得。在這種情況下，可以得到一對直線和。為了避免的情況，可以找到的絕對值最大的對角線元素，更穩定地計算出直線對。

4.1.2 方法二：通過求兩直線相交求解直線

由于兩直線參數的叉乘可得交點，可以進而從中提取出兩直線。對于交點，這里展示兩種求法：

(1) 零空間法:根據(10)可知, 交點在的零空間內，對于的任意零空間向量，有。我們現在必須找到，使得的尺度與(以及)一致。由于，我們有

結合(12),(13)和(18)，可以推導出的范數和的元素之間的關系：

因此，可以將以正確的尺度適當地重新縮放得到交點。

(2) 伴隨矩陣法:矩陣的伴隨矩陣應滿足：

證明：通過(13)可以得到

與相等。

給定一個矩陣，可以得到。為了避免0元素，可以找到其對角線最大的元素和對應的列，交點可以通過將該列除以對角線的平方根得到。

恢復直線：得到交點之后，根據其反對稱矩陣

定義一個新的矩陣

結合(22)和(10)可得。直線對可以通過的行和列得到。

秩為1的情況：如果退化圓錐曲線包括一對重復的直線，則矩陣的秩為1。在這種情況下，可以直接從一行或一列中恢復重復的直線。

4.2 P3P問題求解

退化圓錐曲線中獲得的直線過原二次方程組(7)與(8)的解（交點），因此可以通過求直線與兩個圓錐曲線的交點進行求解。假設第一條直線為：

將(23)代入(5)可得一個關于的二次方程，至多有2個解。需要注意的是，我們只關心正的實數解。得到后，根據(23)可以得到。由可得。代入（3）可得關于的二次方程

由于, 可以得到的解。這種情況下，可以得到的值。由于有一對直線，的解有4種可能。知道后，可以用Gauss-Newton優化(3)的平方和對結果進行細化。之前的工作也使用了類似的細化方法。

求解旋轉和平移：對于每個，首先用(1)消除平移，得到以下方程組

為了找到另一個非共面向量量對應關系，與前人工作一樣，可以使用由三個3D點和圖像點定義的平面的法線（見圖2）。法向量也滿足

其中

結合(25)和(26)，可以解得旋轉

得到旋轉后由(1)可以求解平移。

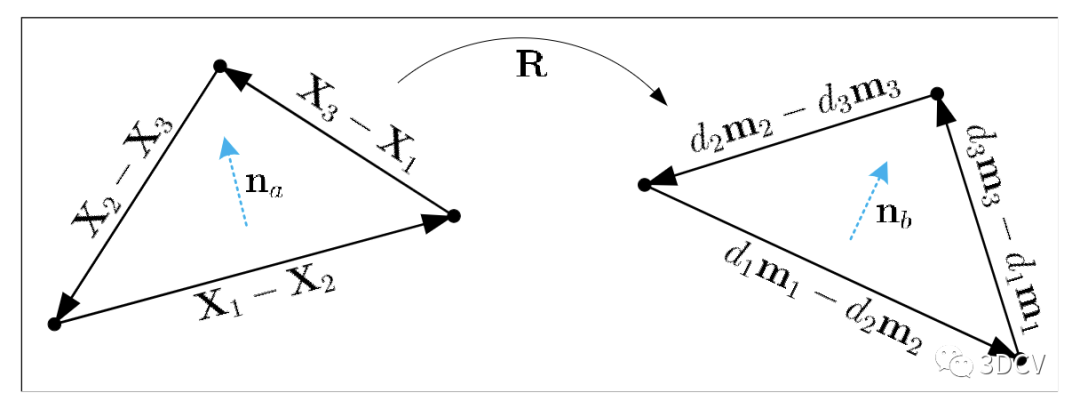
圖2：從向量對應關系到旋轉

4.3 可能解的配置分析以及魯棒算法

以上展示了P3P問題求解的一個通用算法，主要包括2個步驟：

求解構建退化圓錐曲線(式(9));

將退化圓錐曲線分解為兩條直線，進而代入(4)(5)的圓錐曲線求交點

接下來分析解的可能配置，并由此得到魯棒的算法。推薦學習3D視覺工坊近期開設的課程：面向三維視覺算法的C++重要模塊精講：從零基礎入門到進階

（11）中三次方程的通解可能有四種情況：三個實根，一個實根和兩個復根，一個實根和一個重根、一個實三重根。這四種可能性對應于直線和交點的不同情況。在本文的例子中，第一個圓錐曲線（4）是不定的，第二個圓錐曲線（5）是雙曲線（b>0）。不失一般性，假設第一個是橢圓，并在圖3中展示兩個圓錐曲線的可能相對位置。簡要起見，以圖3b作為示例。兩個圓錐曲線有四個實交點，特征三次方程有三個實根，每個實根對應于一對實直線。每對實直線在四個實交點處與兩個圓錐曲線中的任何一個相交（圖3b）。在其他情況下也存在類似的情況。

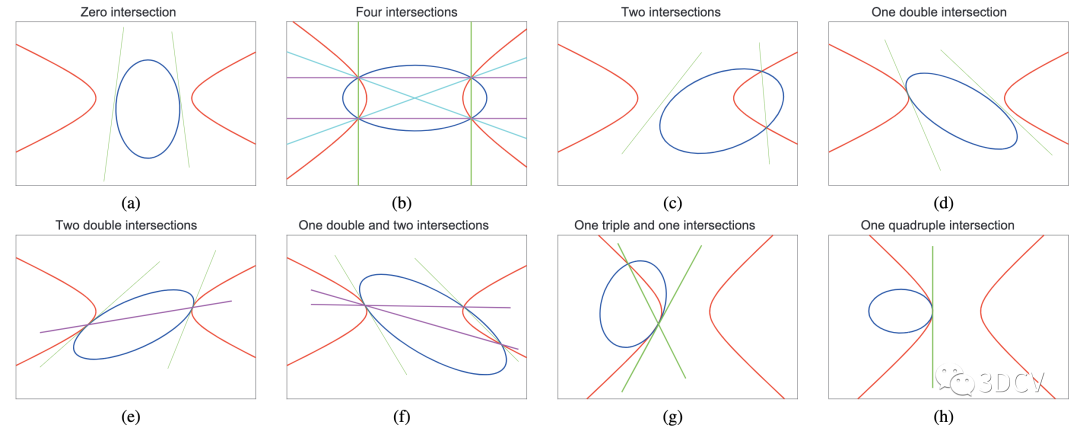
圖3：雙曲線和橢圓相對位置的八種可能情況的圖解。具有不同顏色的一對線對應于不同的三次根。(a)-(c): 兩個圓錐曲線分別具有零、四和兩個實交點的一般情況。(d)-(f): 兩個圓錐曲線相切的臨界情況，分別有一個二重交點、兩個二重交點、一個二重交點和兩個交點。(g)-(h): 兩個圓錐曲線彼此密切（兩個圓錐在切點具有相同的曲率），分別有一個三重交點和一個四重交點

三次方程的根、線的數量和交點之間的關系如表1所示。

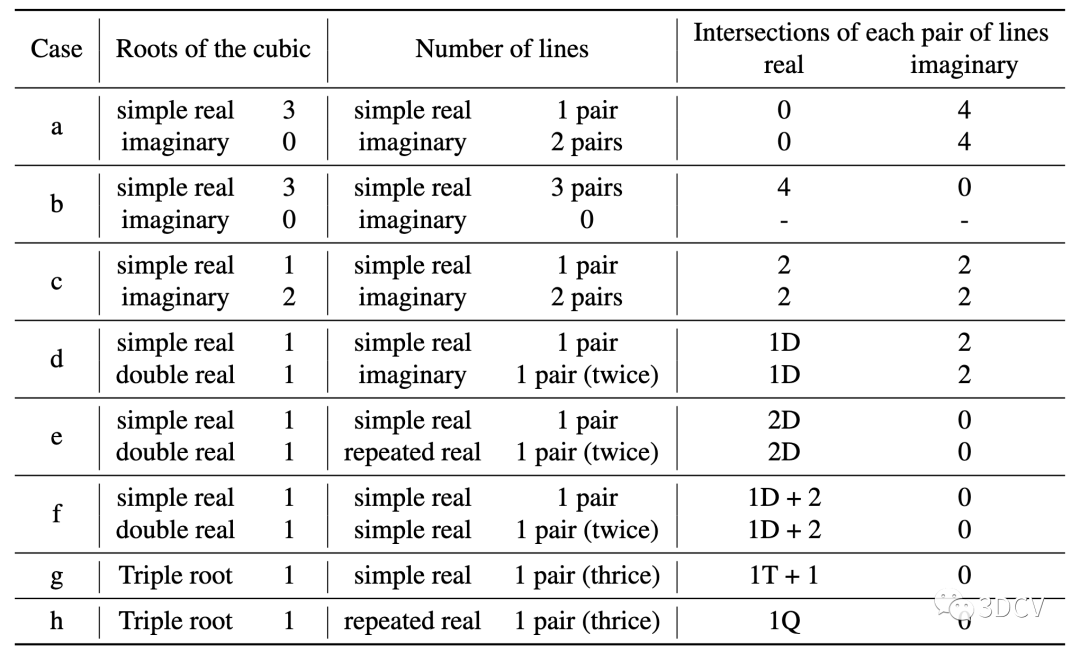
表1：三次方程的根、退化圓錐曲線的直線數和兩個圓錐曲線交點之間的關系。1D、1T和1Q分別表示一個二重交點、一個三重交點和一個四重交點

假設三次方程（11）可以寫成

進行變量替換可得關于的沮喪三次方程(沒有二次項)

其中

(30)的判別式為：

若,（30）有三個不同的實根，其對應于情況（a）和（b）。對于情況（a），由于所有的實根都不對應于任何實交點，我們可以選擇三個根中的任何一個。使用三角解找到根,該根可以對應于一對實線，也可以不對應于實線。如果選擇的實根給出一對實線，可以在驗證第一條直線沒有實交點后跳過第二條直線。對于情況（b），三個根中的任何一個都將產生一對實線和四個實交點。

若,（30）具有一個實根和兩個共軛復根，這對應于情況（c）。使用Cardano公式可以找到實根，并且可以得到一對實直線。如果其中第一條直線與圓錐曲線有實交點，則可以跳過第二條直線。否則，如果第一條直線沒有實交點，就需要檢查第二條直線。

若且,則（30）有一個單實根和一個重實根，這對應于情況（d）、（e）和（f）。對于情況（d），可以看到重實根在虛直線中產生。因此，對于這種情況，可以使用單實數根。

若且，則。在這種情況下，方程（30）有三重根，這對應于情況（g）和（h）。三次方的實根給出了一對實線，并且可以很容易地找到實交點。

基于以上分析和表1，可以注意到，可以使用任何一對實線來恢復實交點，并且除了情況（d）之外，三次方程的任何實根都對應于一對實直線。只需要在且時避免使用重實根。另一方面，如果，則這對直線和圓錐曲線之間一定有雙重交點。為了避免重復的解，需要檢查直線和圓錐曲線之間的交點。整個過程如算法1所示。推薦學習3D視覺工坊三維點云課程：三維點云處理：算法與實戰匯總

5 實驗

5.1 消融實驗

本文提取直線的幾種方法對比

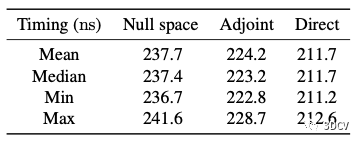
直接法速度最快，但伴隨矩陣法最穩定。實踐中推薦用伴隨矩陣法。

5.2 與SOTA方法對比

5.2.1 數值穩定性

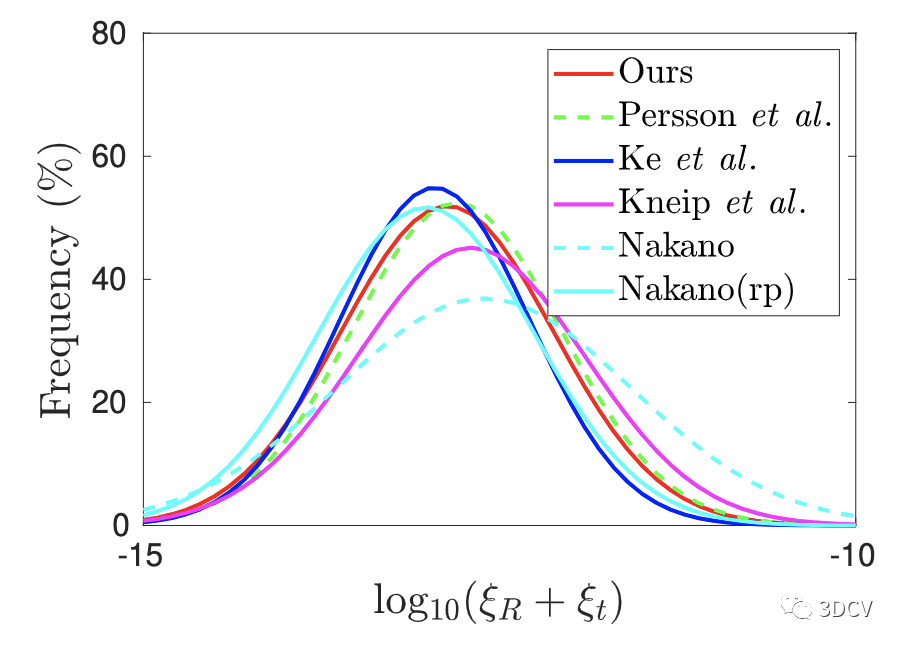
圖4：高斯核平滑直方圖，在無噪聲數據上運行 100,000 次運行的旋轉和平移誤差之和。測量估計和GT之間誤差的 L1 范數。

可以看到所有方法的都是數值穩定的。Nakano(rp)表示帶root polishing(利用Gauss-Newton方法優化根)，該方法更多的分布在小誤差范圍。

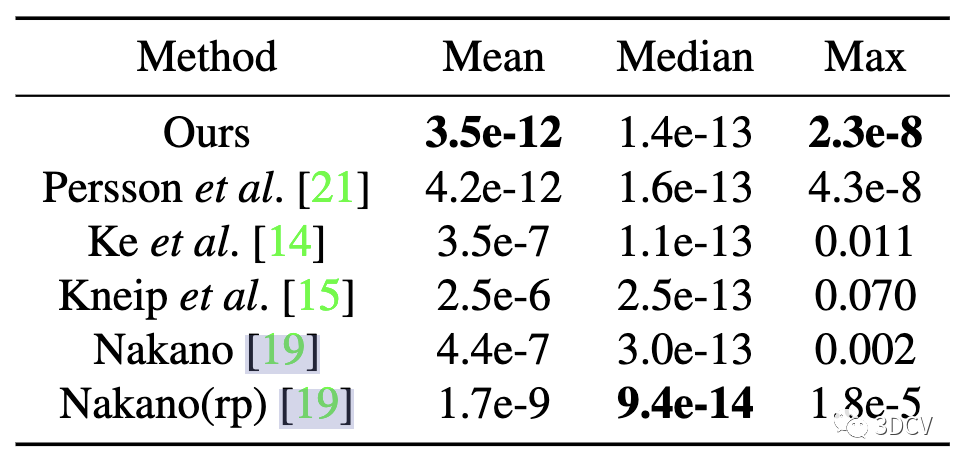
表2：誤差的平均值、中位數和最大值。粗體表示最好的結果

本文提出的求解器在均值誤差和最大誤差上的性能最好，而Nakano(rp)求解器在中值誤差上的性能最好。請注意，基于四次的求解器包含的失敗案例，在此實驗中是刪除了的。

5.2.2 解的對比

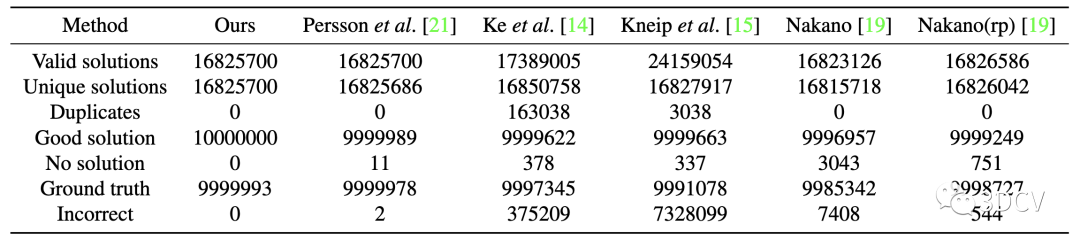
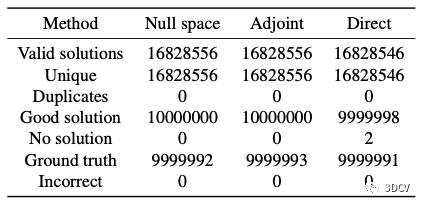
表3：與SOTA求解器對比

本文的求解器優于現有的方法。對于幾乎所有的試驗，都能找到好的解和GT，沒有重復或錯誤的解。基于四次方程的Ke等人和Kneip等人的方法有很多重復解和錯誤解。因為他們用了四次方程的所有4個根(忽略虛部)來找到可能的估計，提高找到GT的可能性是可以的，但會損失其效率，因為實踐中每個假設需要用RANSAC進行評估。Nakano求解器用的虛部閾值過濾不必要的復根，但結果沒有本文的方法好。Ke等人與Kneip等人的方法也能夠用類似的閾值過濾四次方程的根，從而減少重復和錯誤解。

5.2.3 運行時間對比

表4：平均運行時間對比，次嘗試，每個嘗試100次

基于三次方程的求解器比基于四次方程的要更高效，所提出的求解器比SOTA方法快15.4%，加速主要原因有兩個：

基于相對位置和判別式的分析，可以快速選擇三次方程的穩定根，根據判別式的符號可以避免沒必要的計算。

從退化圓錐曲線中恢復直線的方法比Persson等人的方法更高效。本文用C++復現的Nakano方法比原始的MATLAB實現慢，可能是用了不同的矩陣計算庫導致的。

5.3 失敗案例分析

Persson等人的方法在沒有解的情況下，其判別式非常接近于0。這是因為判別式為0對應于圖3中的(d)-(h)這些臨界情況，由于浮點數的舍入誤差和數值不穩定性，這些情況下很難恢復運動參數。本文發現大多數失敗案例是(d)和(f)的情形，(e)(g)(h)很少發生。

與危險圓柱的關系

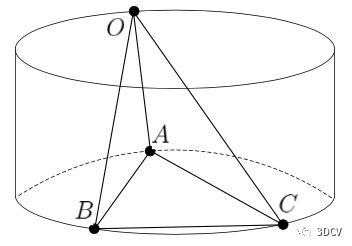
圖5：危險圓柱是指三個3D點A,B,C為圓形環繞點的圓柱，其軸垂直于ABC平面

之前有工作指出，如果光心位于危險圓柱的表面，則P3P問題的解不穩定。本文發現危險圓柱會導致判別式，即對應于圖3中的臨界情形。

5 總結

本文重新審視了 P3P 問題，特別是研究了基于兩個圓錐曲線相交的解法，類似于 Persson 和 Nordberg的方法。通過分析可能的解的集合并明確枚舉極端情況，能夠設計一個快速穩定的 P3P 算法。實驗表明，與以前的方法相比，本文的求解器更魯棒且更快。

局限性

本文的方法基于研究兩個圓錐曲線的實交點。然而，P3P 問題是特殊的，因為解應該是正實數。三次方程可能有更多的約束，不幸的是，本文沒有發現一個很好的方法來做到這一點。請注意，式(4) 和 (5) 可以用同倫延拓來求解，該方法擅長解決大規模平方系統。但對于 P3P 問題，本文發現它不如當前基本上閉式的求解器有效。