大家好，在【深入淺出擴散模型系列】中，我們將從原理到源碼，從基石DDPM到DALLE2，Imagen與Stable Diffusion，通過詳細的圖例和解說，和大家一起來了解擴散模型的奧秘。同時，也會穿插對經典的GAN，VAE等模型的解讀，敬請期待～

本篇將和大家一起解讀擴散模型的基石：DDPM(Denoising Diffusion Probalistic Models)。擴散模型的研究并不始于DDPM，但DDPM的成功對擴散模型的發展起到至關重要的作用。在這個系列里我們也會看到，后續一連串效果驚艷的模型，都是在DDPM的框架上迭代改進而來。所以，我把DDPM放在這個系列的第一篇進行講解。

初讀DDPM論文的朋友，可能有以下兩個痛點：

論文花極大篇幅講數學推導，可是我看不懂。

論文沒有給出模型架構圖和詳細的訓練解說，而這是我最關心的部分。

針對這些痛點，DDPM系列將會出如下三篇文章：

DDPM（模型架構篇）：在閱讀源碼的基礎上，本篇繪制了詳細的DDPM模型架構圖（DDPM UNet），同時附上關于模型運作流程的詳細解說。本篇不涉及數學知識，直觀幫助大家了解DDPM怎么用，為什么好用。

DDPM（人人都能看懂的數學推理篇）：也就是本篇文章，DDPM的數學推理可能是很多讀者頭疼的部分。我嘗試跳出原始論文的推導順序和思路，從更符合大家思維模式的角度入手，把整個推理流程串成一條完整的邏輯線。同樣，我也會配上大量的圖例，方便大家理解數學公式。如果你不擅長數學推導，這篇文章可以幫助你從直覺上了解DDPM的數學有效性；如果你更關注推導細節，這篇文章中也有詳細的推導中間步驟。

DDPM（源碼解讀篇）：在前兩篇的基礎上，我們將配合模型架構圖，一起閱讀DDPM源碼，并實操跑一次，觀測訓練過程里的中間結果。

【如果你粗掃一眼本文，看見大段的公式推導，請不要放棄。出于嚴謹的目的，本文必須列出公式推導的細節；但是，如果你只想把握整體邏輯，完全可以跳過推導，只看結論和圖解，這并不會影響本文的閱讀。最后，看在這滿滿的手打公式和圖片解讀上，如果大家覺得本文有幫助，請多多點贊和在看！】

全文目錄如下：

一、DDPM在做一件什么事

在DDPM模型架構篇中，我們已經討論過DDPM的作用，以及它為何能成為擴散模型/文生圖模型基石的原因。這里為了方便讀者更好了解上下文，我們將相關講解再放一次。

假設你想做一個以文生圖的模型，你的目的是給一段文字，再隨便給一張圖（比如一張噪聲），這個模型能幫你產出符合文字描述的逼真圖片，例如：

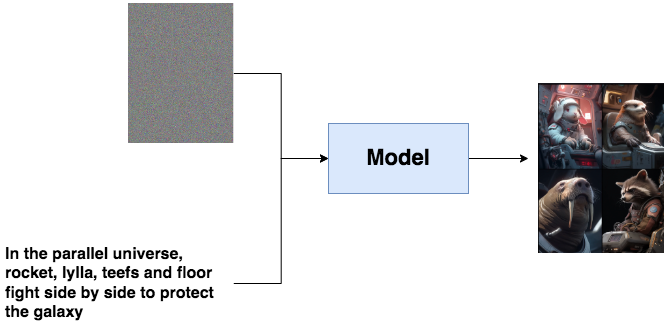
文字描述就像是一個指引(guidance)，幫助模型去產生更符合語義信息的圖片。但是，畢竟語義學習是復雜的。我們能不能先退一步，先讓模型擁有產生逼真圖片的能力？

比如說，你給模型喂一堆cyberpunk風格的圖片，讓模型學會cyberpunk風格的分布信息，然后喂給模型一個隨機噪音，就能讓模型產生一張逼真的cyberpunk照片。或者給模型喂一堆人臉圖片，讓模型產生一張逼真的人臉。同樣，我們也能選擇給訓練好的模型喂帶點信息的圖片，比如一張夾雜噪音的人臉，讓模型幫我們去噪。

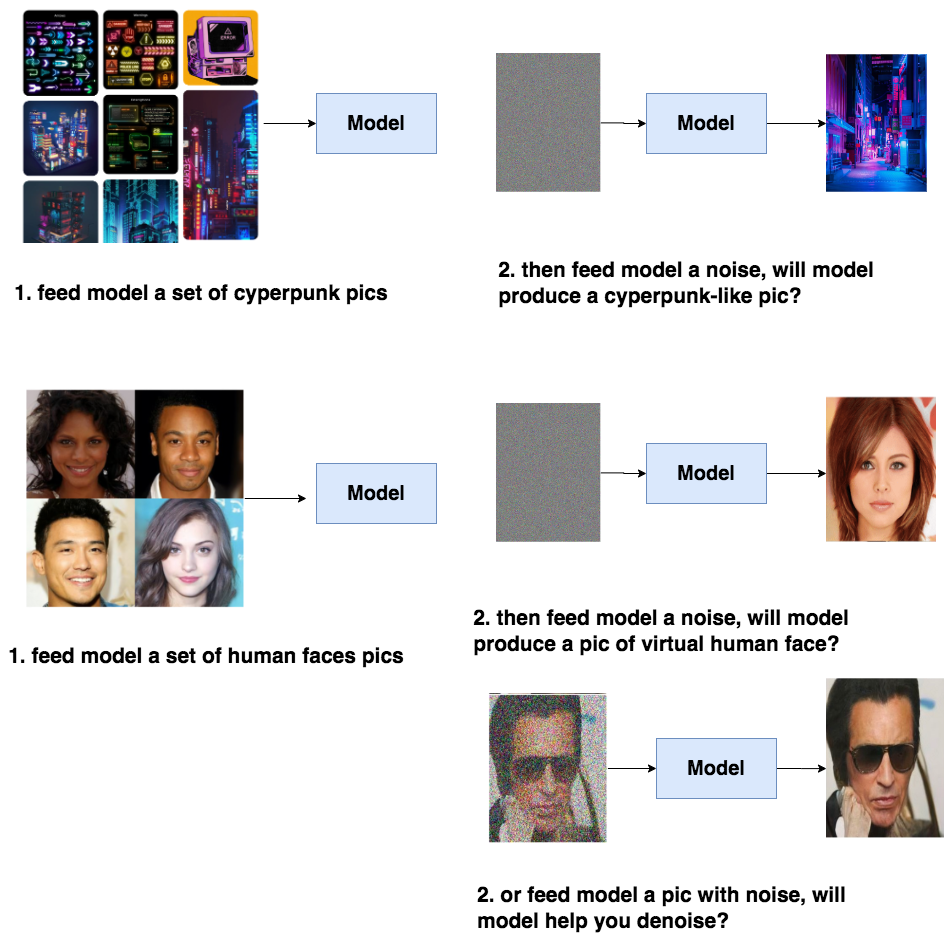
具備了產出逼真圖片的能力，模型才可能在下一步中去學習語義信息(guidance)，進一步產生符合人類意圖的圖片。而DDPM的本質作用，就是學習訓練數據的分布，產出盡可能符合訓練數據分布的真實圖片。所以，它也成為后續文生圖類擴散模型框架的基石。

二、優化目標

現在，我們知道DDPM的目標就是：使得生成的圖片盡可能符合訓練數據分布。基于這個目標，我們記：

：模型所產生的圖片的（概率）分布。其中表示模型參數，以作為下標的目的是表示這個分布是由模型決定的，

：訓練數據（也可理解為真實世界）圖片的（概率）分布。下標data表示這是一個自然世界客觀存在的分布，與模型無關。

則我們的優化目標可以用圖例表示為：

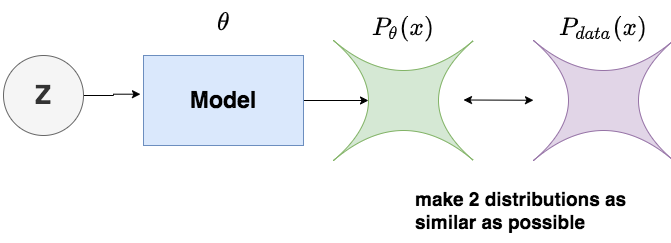
而求兩個分布之間的相似性，我們自然而然想到了KL散度。復習一下KL散度的定義——分布p與分布q之間的KL散度為：

則現在我們的目標函數就變為：我們利用利用式（1.1），對該目標函數做一些變換

經過這一番轉換，我們的優化目標從直覺上的“令模型輸出的分布逼近真實圖片分布”轉變為""，我們也可以把這個新的目標函數通俗理解成“使得模型產生真實圖片的概率最大”。如果一上來就直接把式（1.2）作為優化目標，可能會令很多朋友感到困惑。因此在這一步中，我們解釋了為什么要用式（1.2）作為優化目標。

接下來，我們近一步來看，對式（1.2）還能做什么樣的轉換和拆解。

三、最大化ELBO（Evidence Lower Bound）

的本質就是要使得連乘中的每一項最大，也等同于使得最大。所以我們進一步來拆解。在開始拆解之前，讓我們先回顧一下擴散模型的加噪與去噪過程，幫助我們更好地做數學推理。

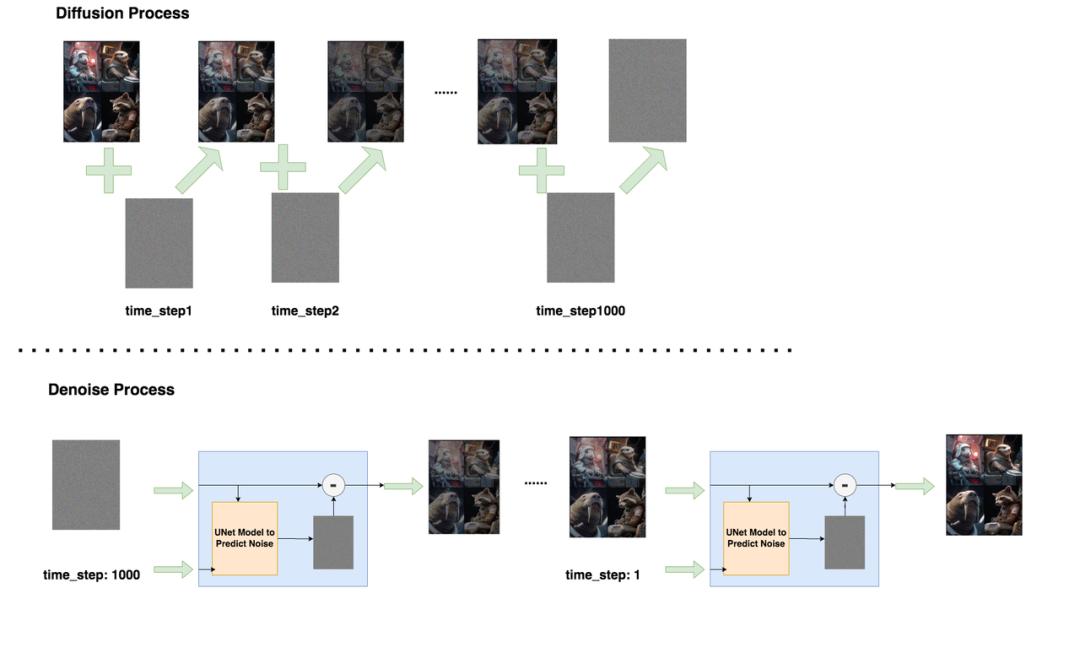
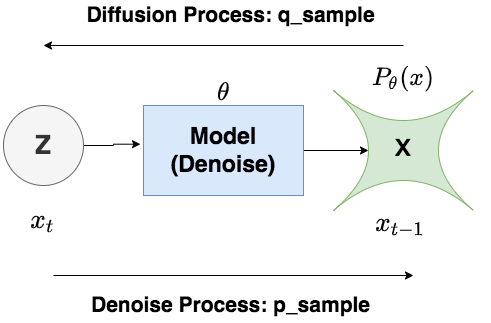
在Diffusion Process中，我們不過模型，而是按照設置好的加噪規則，隨著time_step的變化，給圖片添加噪聲（）。在Denoise Process中，我們則需要經過模型，對圖片進行去噪，逐步將圖片還原成原始的樣子（）。Diffusion過程中遵循的分布，我們記為，Denoise過程中遵循的分布，我們記為。嚴格來說，Diffusion過程遵循的分布應該記為，下標也表示模型參數，也就是說，“規則”也算一種“模型”。理論上，你想對Diffusion單獨訓練一套模型，也是沒有問題的。為了表述嚴謹，我們接下來都將用進行表示。

現在我們可以回到拆解了，即然x和z與Diffusion和Denoise的過程密切相關，那么我們的目標就是要把拆解成用同時表達的形式：

就被稱為Evidence Lower Bound(ELBO)。到這一步為止，我們將最大化拆解成最大化ELBO，其中與diffusion過程密切相關，與denoise過程密切相關。

(2.1)這個公式一出，大家是不是很眼熟？沒錯，它其實也刻畫了VAE的優化目標，所以這里我們才選用z而不是x來表示latent space中的變量。有些讀者可能已經發現了，（2.1）描述的是一個time_step下的優化目標，但是我們的擴散模型，是有T個time_step的，因此，我們還需要把（2.1）再進一步擴展成鏈式表達的方式。在這一步擴展里，我們將不再使用z變量，取而代之的是用來表示，更符合我們對擴散模型的整體理解，則我們有：

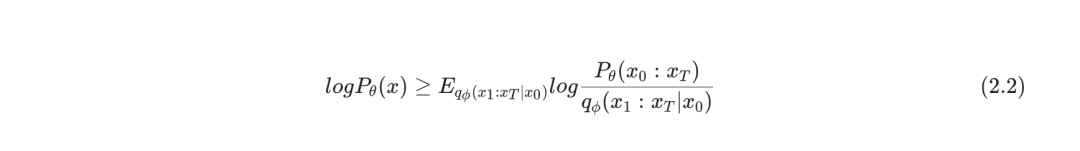
其中，表示從真實世界中篩選出來的干凈的圖片，表示最后一個time_step加噪后的圖片，通常是一個近似純噪聲。細心的讀者可能發現，在（2.2）公式中，左邊的是不是寫成更合理呀？沒錯，因為擴散模型的目標就是去還原來自真實世界的。但這里為了前后表達統一，就不做修改了。讀者們只要理解（2.2）的含義即可。

四、進一步拆解ELBO

復習一下，到這一步為止，我們經歷了如下過程：

首先，總體優化目標是讓模型產生的圖片分布和真實圖片分布盡量相似，也就是

對KL散度做拆解，將優化目標轉變為，同時也等價于讓連乘項中的每一項最大

對做拆解，以優化DDPM其中一個time_step為例，將優化目標轉向最大化下界（ELBO）

以全部time_step為例，將優化目標轉變為，也就是式（2.2）

恭喜你充滿耐心地看到這一步了！接下來，我們還需要再耐心對式（2.2）進行拆解，畢竟現在它只是一個偏抽象的形式，因此我們還需對p與q再做具象化處理。之前我們提過，下標的意思是強調從理論上來說，diffusion過程可以通過訓練一個模型來加噪，而并非只能通過規則加噪。這兩種方法在數學上都是成立的。由于DDPM采用了后者，因此在接下來的過程中，我們將會去掉下標。

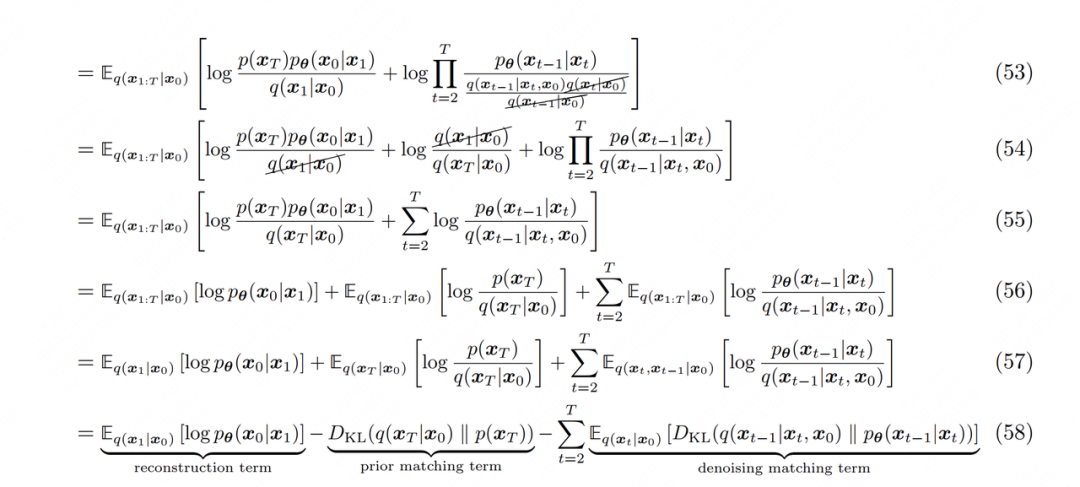
式（2.2）的進一步拆解如下：

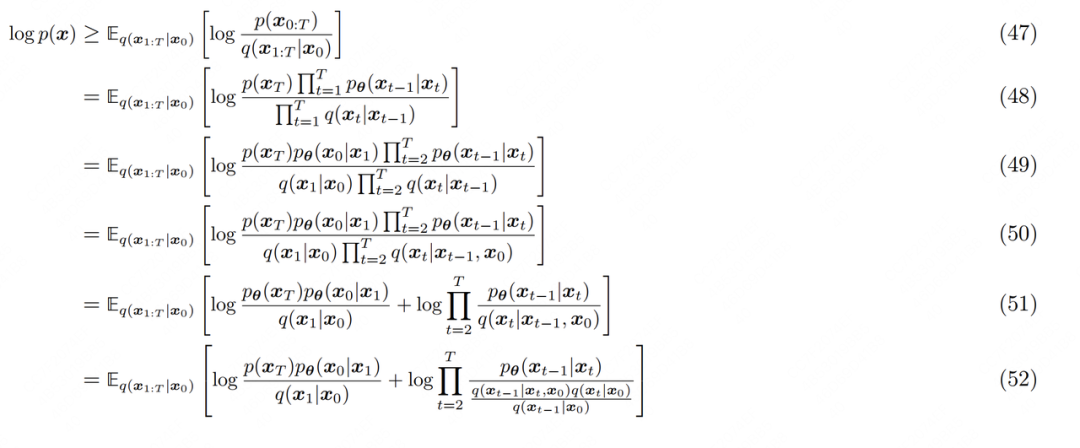
（48）：分子上，因為已是個近似高斯分布的純噪聲，因此它的分布p是已知的，和模型無關，所以將單獨提煉出。分子與分母的其余項則是因為擴散模型遵循馬爾可夫鏈性質，因此可以通過鏈式連乘規則進行改寫

（50)：表示來自真實世界的干凈圖片，它是diffusion過程的起源，任意都可由推導而來，因此可將改寫成

（52）：根據多變量條件概率的貝葉斯鏈式法則進行改寫，即：

當然多變量條件概率的改寫方式有很多種，根據需要我們選擇了上面的這一種

（54）：由于q是既定的，可以看作是一個常量，因此可增加一項

(56)~(57)：根據期望項中涉及到的具體元素，調整期望E的下標

（58）：根據KL散度的定義重寫最后兩項。其中prior matching term可看作是常量，reconstruction term和denoising matching term則是和模型密切相關的兩項。由于兩者間十分相似，因此接下來我們只需要特別關注denoising matching term如何拆解即可。

五、重參數與噪聲預測

現在，我們的優化目標轉為最大化，我們繼續對該項進行拆解。

首先我們來看一項。

根據多變量條件概率的鏈式法則，我們有：

現在，我們分別來看，，具體長什么樣子。

5.1 重參數

5.1.1 為什么需要重參數

回顧模型架構篇，我們曾經提過，最樸素的diffusion加噪規則是，在每一個time_step中都sample一次隨機噪聲，使得：

在架構篇中，我們直接指出，即篩選的噪聲是來自一個標準高斯分布。但是為什么要這么設計呢？

我們假設真實世界的圖片服從這樣的高斯分布，而現在我們的模型就是要去學習這個分布，更具象點，假設模型遵從的分布是，我們的目的就是讓逼近，逼近。

那么在diffusion過程中，更符合直覺的做法是，模型從采樣出一個噪聲，然后在denoise的過程中去預測這個噪聲，這樣就能把梯度傳遞到上，使得模型在預測噪聲的過程中習得真實圖片的分布。

但這樣做產生的問題是，實際上梯度并不能傳遞到上。舉個簡單的例子，假設你從隨機采樣出了一個3，你怎么將這個隨機的采樣結果和聯系起來呢？也就是說，在diffusion過程中，如果我們從一個帶參數的分布中做數據采樣，在denoise過程中，我們無法將梯度傳遞到這個參數上。

針對這個問題，有一個簡單的解決辦法：我從一個確定的分布（不帶參數）中做數據采樣，不就行了嗎？比如，我從先采樣出一個，然后再令最終的采樣結果z為：。這樣我不就能知道z和間的關系了？同時根據高斯分布性質，z也服從分布。

以上“從一個帶參數的分布中進行采樣”轉變到“從一個確定的分布中進行采樣”，以解決梯度無法傳遞問題的方法，就被稱為“重參數”（reparamterization）。關于重參數原理的更多細節，推薦大家閱讀這篇文章（https://spaces.ac.cn/archives/6705）

5.1.2 重參數的具體方法

到這一步根據重參數的思想，我們可以把轉變為了。但是現在的diffusion過程還是太繁瑣：每一個time_step都要做一次采樣，等我后續做denoise過程去預測噪聲，傳播梯度的時候，參數不僅在這個time_step有，在之前的一系列time_steps中都有，這不是給我計算梯度造成困擾了嗎？注意到在diffusion過程中，隨著time_step的增加，圖片中含有的噪聲是越來越多的，那我能不能設定一個函數，使得每個time_step的圖片都能由原始圖片加噪推導而來，然后使得噪聲的比例隨著time_step增加而變大？這樣我不就只需要一次采樣了嗎？

當然沒有問題，DDPM采用的做法是：

（1）首先，設置超參數，滿足隨著t增大，逐漸變大。

（2）令：

易推出隨著t增大而逐漸變小

（3）則任意時刻的都可以由表示出：

我們通過圖例來更好理解上面的三步驟：

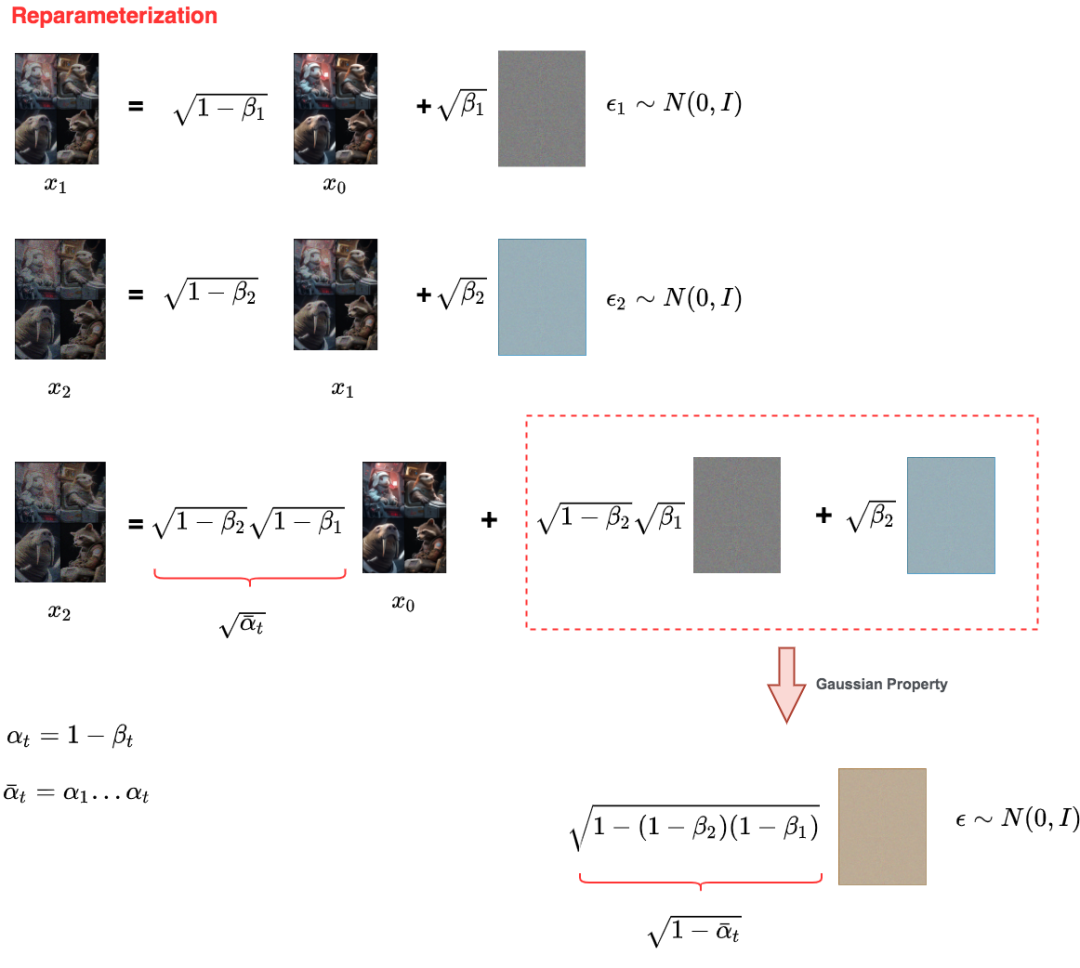
詳細的過程都在圖例中表示出了，這里不做贅述。

5.2 噪聲預測

講完了重參數的部分，我們繼續回到剛才拆解的步驟上來，復習一下，我們已經將ELBO拆解成，現在我們的關注點在q分布上，而q分布又由以下三項組成：

，我們繼續來看這三項要怎么具體表示出來。

由章節5.1.2，我們知道：

則任意的關系都可以由此推出：

(友情提示：大家記得看5.1.2中的圖例區分哦，不是typo)。

同時，我們已經知道（假設）都服從高斯分布，則根據高斯分布的性質，我們有：

對于高斯分布，知道了均值和方差，我們就可以把它具體的概率密度函數寫出來：

經過這樣的一頓爆肝推導，我們終于將的分布寫出來了（84）。也就是我們當前優化目標中的q部分。

現在，我們來看部分，根據優化目標，此時我們需要讓p和q的分布盡量接近：

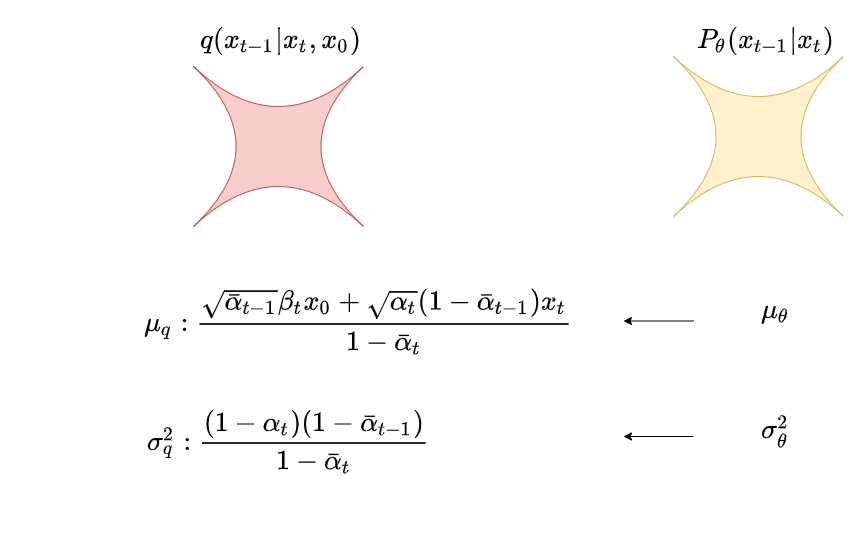
而讓p和q的分布接近，等價與讓。注意到其實是一個常量，它只和超參有關。在DDPM中，為了簡化優化過程，并且使訓練更穩定，就假設也按此種方式固定下來了。在后續的擴散模型（例如GLIDE）中，則引入對方差的預測。在DDPM中，只預測均值。

好，那么預測均值，到底是在預測什么東西呢？我們對再做改寫，主要是根據我們設置的diffusion規則，將用進行表示：

觀察到，式（5.1）的結果在diffusion過程中就已決定好。所以現在對于，我只要讓它在denoise的過程里，預測出，使得，然后令：

這樣，我不就能使得和的分布一致了嗎！

此刻！是不是一道光在你的腦海里閃過！一切都串起來了，也就是說，只要在denoise的過程中，讓模型去預測噪聲，就可以達到讓“模型產生圖片的分布”和“真實世界的圖片分布”逼近的目的！

5.3 再次理解training和sampling

現在，我們再來回顧training和sampling的過程，在training的過程中，我們只需要去預測噪聲，就能在數學上使得模型學到的分布和真實的圖片分布不斷逼近。而當我們使用模型做sampling，即去測試模型能生成什么質量的圖片時，我們即可由式(5.1)中的推導結論，從推導，直至還原出。注意到這里，其中是我們式（5.1）中要逼近的均值真值；，則正是我們已經固定住的方差。

關于training和sampling更詳細的實操解說，可以參見模型架構篇。

六、總結（必看）

恭喜你堅持看到了這里！我們來把整個推導串成完整的邏輯鏈：

（1）首先，DDPM總體優化目標是讓模型產生的圖片分布和真實圖片分布盡量相似，也就是。同時，我們假設真實世界的圖片符合高斯分布：。因此我們的目標就是要讓習得

（2）但是這兩個客觀存在的真值是未知的，因此我們必須對KL散度進行不斷拆解，直至能用確定的形式將它表示出來。

（3）對KL散度做初步拆解，將優化目標轉變為，同時也等價于讓連乘項中的每一項最大

（4）繼續對做拆解，以優化DDPM其中一個time_step為例，將優化目標轉向最大化下界（ELBO）

（5）依照馬爾可夫性質，從1個time_step推至所有的time_steps，將（4）中的優化目標改寫為，也就是式（2.2）

（6）對式（2.2）繼續做拆解，將優化目標變為

（7）先來看（6）中的一項，注意到這和diffusion的過程密切相關。在diffusion的過程中，通過重參數的方法進行加噪，再經過一頓爆肝推導，得出，易看出該分布中方差是只和我們設置的超參數相關的常量。

（8）再來看（6）中的一項，下標說明了該項和模型相關。為了讓p和q的分布接近，我們需要讓p去學習q的均值和方差。由于方差是一個常量，在DDPM中，假設它是固定的，不再單獨去學習它（后續的擴散模型，例如GLIDE則同時對方差也做了預測）。因此現在只需要學習q的均值。經過一頓變式，可以把q的均值改寫成。因此，這里只要讓模型去預測噪聲，使得，就能達到達到（1）中的目的！

七、參考

在學習DDPM的過程中，我也看了很多參考資料，但發現很難將整個推導過程串成一條符合思維慣性的邏輯鏈，因此對很多細節也是一知半解。直到我看到李宏毅老師對擴散模型原理的講解（從分布相似性入手），以及閱讀了google的一篇關于擴散模型數學推理的綜述，才恍然大悟。自己動手推導后，從更符合我慣性思維的角度入手，寫了這篇文章。因此，我也把我認為非常有幫助的參考資料列在下面，大家可以補充閱讀。