高通濾波器將允許高于截止頻率的頻率，并衰減低于截止頻率的頻率。在某些情況下，此濾波器也稱為“低切”濾波器或“基切”濾波器。衰減量或通帶范圍將取決于濾波器的設計參數。

有源濾波器的通帶增益大于單位增益。有源高通濾波器的工作原理與無源高通濾波器相同，但主要區別在于有源高通濾波器使用運算放大器，它提供輸出信號的放大和控制增益。

高通濾波器的理想特性如下所示。

我們知道，高通濾波器會將頻率從截止頻率點傳遞到“無窮大”頻率，這在實際考慮中是不存在的。除了該有源高通濾波器中的無源高通濾波器外，最大頻率響應還受到運算放大器開環特性的限制。

有源高通濾波電路

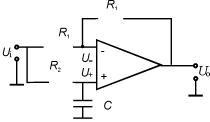
通過將無源RC高通濾波器電路連接到運算放大器的反相或同相端子，我們可以得到一階有源高通濾波器。連接到單位增益運算放大器同相端的無源RC高通濾波電路如下圖所示。

ThegainAmax=1andcutofffrequencyfc=1/2πRC

具有高電壓增益的有源高通濾波器

其操作與無源高通濾波器相同，但輸入信號由輸出端的放大器放大。放大量取決于放大器的增益。

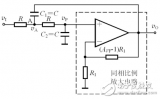
通帶增益的幅度等于1+（R3/R2).其中R3是反饋電阻，單位為Ω（歐姆）和R2是輸入電阻。帶放大的有源高通濾波器電路如下

高通濾波器的電壓增益

電壓增益Av=A.max（f/fc）/√{1+（f/fc）2}

其中f=工作頻率

fc=截止頻率

A.max=濾波器的通帶增益=1+（R3/R2)

在低頻時，即當工作頻率小于截止頻率時，電壓增益小于通帶增益A.max.在高頻下，即當工作頻率大于截止頻率時，濾波器的電壓增益等于通帶增益。

如果工作頻率等于截止頻率，則濾波器的電壓增益等于0.707A.max.

電壓增益（分貝）

電壓增益的大小通常以分貝（dB）為單位：

Av（dB）=20對數10（Vout/Vin)

-3dB=20log10（0.707*Vout/Vin)

分隔通帶和阻帶的截止頻率可以使用以下公式
fC=1/（2πRC）

有源高通濾波器的相移等于無源濾波器的相移。它等于截止頻率fC處的+45°，該相移值等于

?=tan-1（1/2πfcRC）

有源高通濾波器的頻率響應

相對于放大器開環增益的頻率響應曲線如下所示。

在有源高通濾波器的頻率響應中，最大通帶頻率受帶寬或運算放大器開環特性的限制。由于此限制，有源高通濾波器響應將類似于寬帶濾波器響應。

通過使用這種基于運算放大器的有源高通濾波器，我們可以通過使用低容差電阻和電容器來實現高精度。

采用反相運算放大器的高通有源濾波器

我們知道，有源高通濾波器可以通過使用運算放大器的反相端或同相端來設計。到目前為止，我們看到了同相有源高通濾波器的高通濾波器電路和響應曲線。現在讓我們看看使用反相運算放大器的有源高通濾波器。

拉普拉斯形式的增益推導

讓我們考慮如下所示的反相放大器。

輸入阻抗Z1=1/sC1

其中s=拉普拉斯變量

C1=電容

電路中流動的電流為I1、I2和Iin，

其中I1=I2且Iin=0

Vin/Z1=-Vout/R1

Vout/Vin=–R1/Z1

Vout/Vin=–R1/(1/sC1)

Vout/Vin=-sR1C1=Gain

有源高通濾波器示例

我們將截止頻率值視為10KHz，通帶增益A.max為1.5，電容值為0.02μF

截止頻率的公式為fC=1/（2πRC）

通過重新排列這個方程，我們有R=1/（2πfC）

R=1/（2π100000.02*10-6)=795.77?

濾波器的通帶增益為A.max=1+（R3/R2）=1.5

R3=0.5R2

如果我們將R2值視為10KΩ，則R3=5kΩ

我們可以按如下方式計算濾波器的增益

高通濾波器的電壓增益|Vout/Vin|=A.max*（f/fc）/√[1+（f/fc）2]

通過使用這個方程，讓我們將頻率范圍的響應制成表格，以繪制濾波器的響應曲線。這些響應假定為10Hz至100KHz。

波特圖

為了分析電路頻率響應，使用此波特圖。它只不過是線性、時變與頻率的傳遞函數的曲線。這是用對數頻率軸繪制的。它主要由兩個地塊組成;一個是幅度圖，另一個是相位圖。

幅度圖將表示頻率響應的幅度，即增益，相位圖用于表示頻移的響應。

根據上表值的頻率響應波特圖如下所示：

根據計算的值，在頻率10Hz時，以dB為單位獲得的濾波器增益為-56.48。如果我們將頻率值增加到100Hz，則獲得的增益為-36.48dB，在頻率為500Hz時，濾波器的增益為-22.51dB。

在頻率1000Hz時，以dB為單位的增益為-16.52。我們可以說，如果頻率增加，濾波器的增益將以20dB/十倍頻程的速率增加。

截止頻率為10KHz時，濾波器的增益增加，但在截止頻率之后，增益達到最大值且恒定。

二階高通濾波器

二階有源濾波器頻率響應與二階有源低通濾波器響應完全相反，因為該濾波器會將電壓衰減到截止頻率以下。二階濾波器的傳遞函數如下所述Vout(s)/Vin(s)=-Ks2/s2+(ω0/Q)s+ω02

WhereK=R1/R2andω0=1/CR

這是二階高通濾波器的一般形式。

二階有源高通濾波器電路

二階有源濾波器的設計過程與一階濾波器的設計過程相同，因為唯一的變化是滾降。如果一階有源高通濾波器的滾降為20dB/十倍頻程，則二階濾波器的滾降為40dB/十倍頻程。

它表示一階濾波器值的兩倍。二階濾波器的電路如下所示。

濾波器的增益為1+R1/R2，截止頻率的公式為fc=1/2π√R3R4C1C2

二階有源高通濾波器示例

我們設計一個截止頻率為4KHz的濾波器，阻帶中的延遲率為40dB/十倍頻程。由于阻帶中的延遲率為40dB/十倍頻程，我們可以清楚地說該濾波器是二階濾波器。

我們考慮電容值為C1=C2=C=0.02μF

截止頻率的公式為R=1/2πfC

通過重新排列這個方程，我們得到R=1?2πfC

將截止頻率值代入4KHz，將電容值代入0.02μF

R=1.989KΩ=2KΩ。

設濾波器增益為1+R1/R2=2

R1/R2=1

R1=R2

因此我們可以取R1=R2=10KΩ

因此，得到的濾波器如下所示。

高階高通濾波器

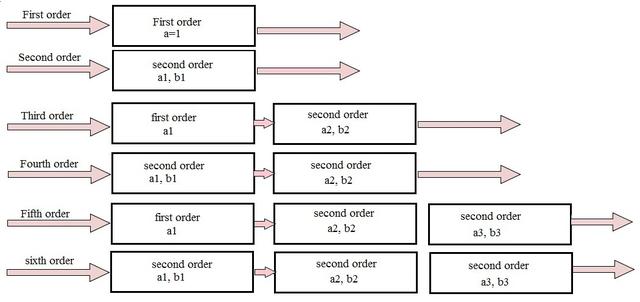
通過級聯一階濾波器和二階濾波器，我們可以得到三階濾波器。當我們級聯兩個二階濾波器時，我們可以得到四階濾波器。像這樣，在一階和二階濾波器的幫助下，我們得到了高階濾波器。

隨著濾波器階數的增加，實際阻帶與理論阻帶之差增大。但是高階濾波器的總增益是相等的，因為我們已經看到決定頻率響應值的電阻和電容是相同的。

此級聯順序如下所示。

有源高通濾波器的應用

• 這些用于揚聲器中以減少低電平噪音。
• 消除音頻應用中的隆隆聲失真，因此這些也稱為高音增強濾波器。
• 這些用于音頻放大器中以放大更高頻率的信號。
• 這些也用于均衡器。