濾波器是一種用于過濾信號的電路,它將僅傳遞所需的信號并避免不需要的信號。通常,濾波器由無源元件或有源元件設計。
低通濾波器是一種僅通過低頻信號并衰減或停止高頻信號的濾波器。它只允許來自0Hz的信號切斷頻率“fc”。該截止頻率值將取決于電路中使用的元件的值。
通常,這些濾波器優選低于頻率100kHz。截止頻率也稱為分斷頻率或翻轉頻率。
無源低通濾波器
由無源元件設計的低通濾波器電路稱為無源低通濾波器。
下圖顯示了RC低通濾波器的簡單電路。
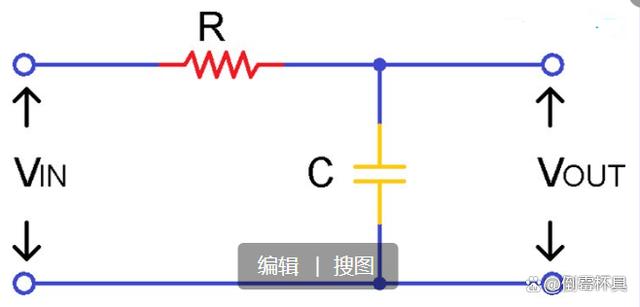
只需將電阻“R”與電容器“C”串聯即可獲得RC低通濾波器。它可以簡稱為低通濾波器(LPF)。電阻器與電路中施加頻率的變化無關,但電容器是一種敏感元件,這意味著它響應電路中的變化。
由于它只有一個電抗元件,因此該電路也可以稱為“單極點濾波器”或“一階濾波器”。輸入電壓“Vin”串聯施加到電阻器,輸出電壓僅取在電容器兩端。
由于電容器是一種敏感元件,因此要觀察的主要濃度是“容抗”。容抗是由電路中的電容器產生的反對響應。
為了保持電容器的電容,電容器將反對電路中的少量電流流動。這種對電路中電流的反作用稱為阻抗。因此,容抗隨著相反電流的增加而降低。
這樣我們可以說容抗與施加到電路的頻率成反比。電阻的電阻值是穩定的,而電容電抗值是變化的。與電容器的電壓電位相比,電容器兩端的壓降非常小。
這意味著在低頻時,壓降很小,電壓電位很大,但在高頻下,壓降非常高,電壓電位較小。通過這種現象,我們可以說上述電路可以充當“變頻分壓器”電路。
容抗可公式化如下:

輸出電壓計算
為了得到分壓器方程,我們必須考慮阻抗、容抗、輸入電壓和輸出電壓。通過使用這些項,我們可以將RC電位分頻器方程公式表述如下:
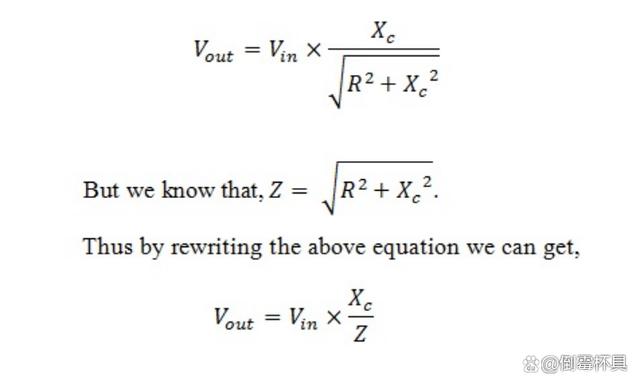
通過使用這個方程,我們可以計算任何應用頻率下的輸出值。
低通濾波器示例
讓我們通過考慮電阻和電容值來檢查這些輸出電壓值和容抗值。假設電阻R的值為4.7kΩ,電容值為47nF。提供的輸入交流電壓為10V。我們要計算的頻率值為1kHz和10kHz。

這樣我們可以清楚地說,當頻率增加時,容抗會降低。不僅容抗降低,輸出電壓也降低。
從上面的例子中可以看出,隨著頻率從3386kHz增加到27kHz,電容電抗從338.62歐姆降低到5.84歐姆,輸出電壓從0.718伏降低到1.10伏。
低通濾波器的頻率響應
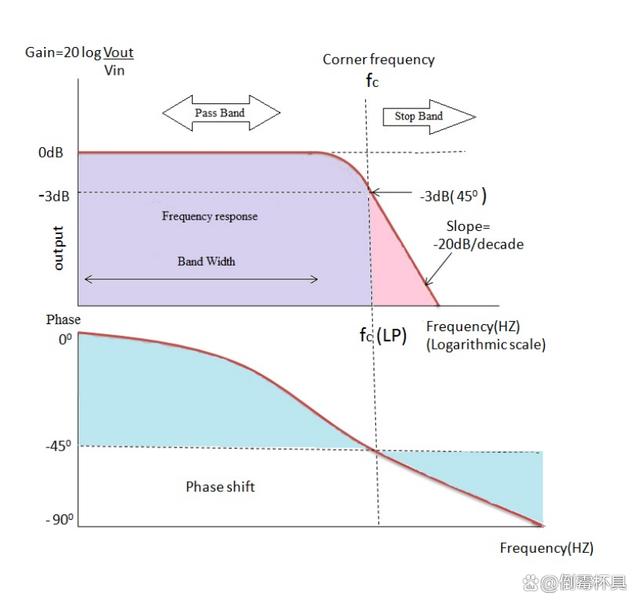
從過濾器的介紹中,我們已經看到震級|H(jω)|的濾波器取電路的增益。該增益測量為20log(V 外 ,5 在 ),對于任何RC電路,斜率“滾降”的角度為-20dB/十倍頻程是相同的。
截止區域以下的頻率帶稱為“通帶”,截止頻率之后的頻率帶稱為“阻帶”。從圖中可以觀察到通帶是濾波器的帶寬。
從該圖中可以清楚地看出,在截止頻率之前,增益是恒定的,因為輸出電壓與低頻下的頻率值成正比。這是由于容抗在低頻下的作用類似于開路,并允許最大電流通過高頻電路。容抗值在低頻時非常高,因此具有更大的能力來阻止流過電路的電流。
一旦達到截止頻率值,輸出電壓就會逐漸降低并達到零。增益也隨著輸出電壓的降低而降低。截止頻率后,電路斜率的響應將達到滾降點,該滾降點發生在-20dB/十倍頻程。
這主要是由于頻率的增加,當頻率增加時,容抗值降低,因此阻斷電流通過電容器的能力降低。當通過電路的電流增加時,由于電容器的電容有限,電路會發生短路。因此,濾波器的輸出電壓在高頻時為零。
避免此問題的唯一方法是選擇這些電阻和電容器可以承受的頻率范圍。電容器和電阻的值起著主要作用,因為根據這些值,只有截止頻率“fc”取決于。如果頻率范圍在截止頻率范圍內,那么我們可以克服短路問題。
當電阻值和容抗值重合時,將發生此截止點,這意味著電阻和無功電容的矢量和相等。那是當R=Xc在這種情況下,輸入信號衰減-3dB/十倍頻程。
該衰減約為輸入信號的70.7%。電容器極板的充電和放電所需的時間根據正弦波而變化。因此,輸出信號的相位角(?)在截止頻率后滯后于輸入信號。在截止頻率下,輸出信號錯相-45°。
如果濾波器的輸入頻率增加,則電路輸出信號的滯后角增加。只是對于更多的頻率值,電路更異相。
電容器有更多的時間在低頻下對極板進行充電和放電,因為正弦波的開關時間更長。但隨著頻率的增加,切換到下一個脈沖所需的時間逐漸減少。因此,會發生時間變化,從而導致輸出波的相移。
無源低通濾波器的截止頻率主要取決于濾波電路中使用的電阻和電容值。該截止頻率與電阻和電容值成反比。無源低通濾波器的截止頻率由下式給出
f C =1/(2πRC)
無源低通濾波器的相移為下式
相移(?)=–tan ^-1^ (2πfRc)
時間常數(τ)
正如我們已經看到的,電容器相對于輸入正弦波對極板進行充電和放電所花費的時間會導致相位差。電阻和電容串聯會產生這種充放電效果。
串聯RC電路的時間常數定義為電容器充電至最終穩態值的63.2%所花費的時間,也定義為電容器放電至穩態值的36.8%所花費的時間。此時間常數用符號'τ'表示。
時間常數與截止頻率的關系如下
時間常數τ=RC=1/2πfc和ω ~c~ =1/τ=1/RC
我們也可以重寫為截止頻率
這樣,我們可以說濾波器的輸出取決于施加在輸入端的頻率和時間常數。
無源低通濾波器示例2
我們來計算低通濾波器的截止頻率,該濾波器的電阻為4.7k,電容為47nF。
我們知道截止頻率的公式為
fc=1/2πRC=1/(2πx4700x47x10 ^-9^ )=720Hz
二階無源低通濾波器
到目前為止,我們已經研究了一階低通濾波器,它是通過串聯電阻器和電容器制成的。然而,有時單級可能不足以消除所有不需要的頻率,因此使用二階濾波器,如下所示。
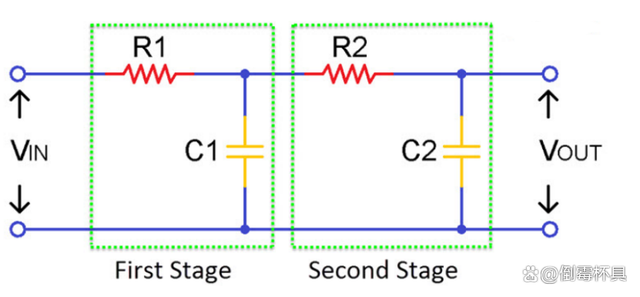
只需在一階低通濾波器上再增加一級即可獲得二階低通RC濾波器。該濾波器的斜率為-40dB/十倍頻程或-12dB/倍頻程,四階濾波器的斜率為-80dB/倍頻程,依此類推。
無源低通濾波器截止頻率下的增益為
A=(1/√2)^n^
其中n是階段的順序或數量
二階低通濾波器的截止頻率由下式給出
fc=1/(2π√(R1C1R2C2))
二階低通濾波器-3dB頻率為:
f (-3分貝) =FC√(2 ^(1/n)^ –1)
其中fc是截止頻率,n是級數,?-3分貝是-3dB通帶頻率。
低通濾波器摘要
低通濾波器由電阻器和電容器組成。不僅是電容器,任何帶電阻的電抗元件都會提供低通濾波器。它是一種僅允許低頻并衰減高頻的濾波器。
低于截止頻率的頻率稱為通帶頻率,大于截止頻率的頻率稱為阻帶頻率。通帶是濾波器的帶寬。
濾波器的截止頻率取決于為電路設計選擇的元件值。截止頻率可以使用以下公式計算。
f C =1/(2πRC)
濾波器的增益取為濾波器的幅度,增益可以使用公式20對數(V out /V in ).濾波器的輸出是恒定的,直到頻率電平達到截止頻率。
在截止頻率下,輸出信號為輸入信號的70.7%,截止頻率后輸出逐漸降低到零。截止頻率后,輸出信號的相位角滯后于輸入信號。
在截止頻率下,輸出信號相移為45°。
如果我們在低通濾波器電路中互換電阻和電容的位置,那么電路的行為就像高通濾波器一樣。
對于正弦輸入波,電路的行為類似于一階低通濾波器。一階濾波器的操作我們已經研究過了,但是當輸入信號類型發生變化時,必須觀察濾波器輸出會發生什么。
當我們將輸入信號類型更改為開關模式(ON/OFF)或方波時,電路的行為類似于積分器,討論如下。
低通濾波器作為波形整形電路
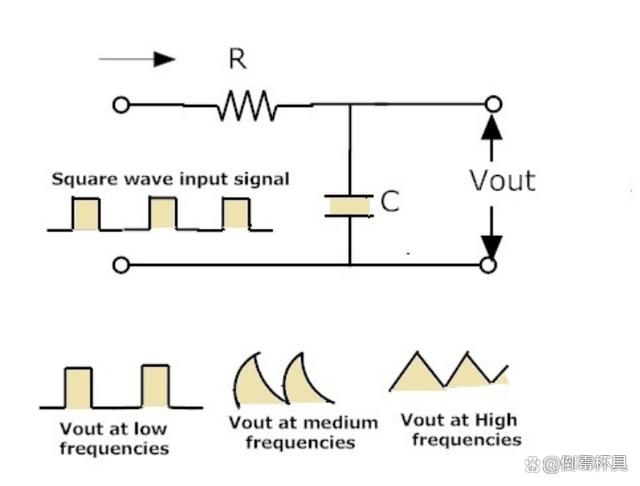
上圖顯示了濾波器在方形輸入方面的性能。當低通濾波器的輸入是方波時,獲得的濾波器輸出將是三角形的。
這是因為電容器不能充當ON或OFF開關。在低頻下,當濾波器的輸入是方波時,輸出也將僅處于方波中。
當頻率增加時,濾波器的輸出看起來像三角波。如果我們增加頻率,則輸出信號的幅度會減小。
三角波是由于電容器的作用或簡單的電容器的充放電模式而引起的三角波。
低通濾波器的應用
· 低通濾波電路的主要用途是避免整流器輸出中的交流紋波。
低通濾波器用于音頻放大器電路。
· 通過使用這種無源低通濾波器,我們可以直接將立體聲系統中的高頻噪聲降低到小干擾模式。
· 低通濾波器作為積分器可用作波形整形和波發生電路,因為可以輕松地將一種類型的電信號轉換為另一種形式。
· 它們也用于解調器電路,以從調制信號中提取所需的參數。
-
電容器
+關注
關注
63文章
6199瀏覽量
99306 -
串聯電阻
+關注
關注
1文章
190瀏覽量
14766 -
調制解調器
+關注
關注
3文章
850瀏覽量
38774 -
低通濾波器
+關注
關注
14文章
471瀏覽量
47327 -
晶體管
+關注
關注
77文章
9634瀏覽量
137844
發布評論請先 登錄
相關推薦
有源濾波器和無源濾波器的區別?
RC無源低通濾波器設計問題?
無源濾波器的相關資料推薦
RC無源濾波器電路
無源RC濾波器設計性的實驗方案構思資料說明
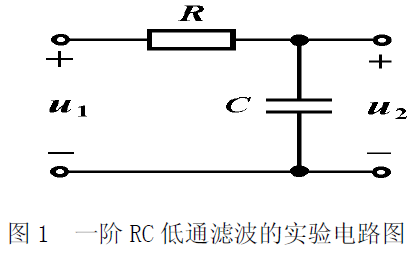
濾波電路(上),無源濾波器





 無源低通RC濾波器設計
無源低通RC濾波器設計










評論