串聯(lián)和并聯(lián)電阻器

電阻器可以單獨(dú)串聯(lián)連接，也可以單獨(dú)并聯(lián)連接。一些電阻電路由串聯(lián)和并聯(lián)網(wǎng)絡(luò)的組合組成，以開(kāi)發(fā)更復(fù)雜的電路。這些電路通常稱為混合電阻電路。即使這些電路組合了串聯(lián)和并聯(lián)電路，計(jì)算等效電阻的方法也沒(méi)有變化。

單個(gè)網(wǎng)絡(luò)的基本規(guī)則，如“相同的電流流過(guò)串聯(lián)電阻器”和“并聯(lián)電阻器兩端的電壓相同”適用于混合電路。

混合電阻電路示例如下所示

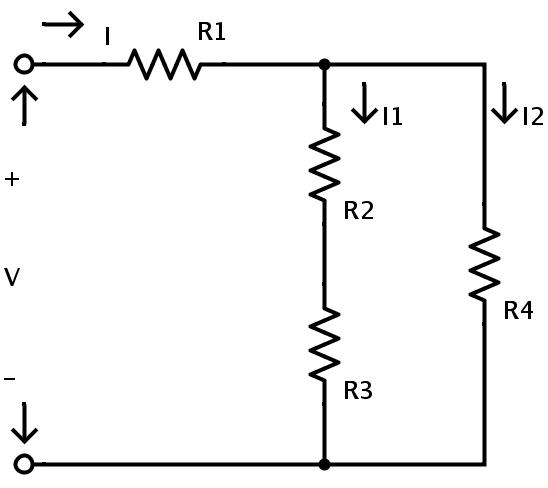
它由混合電阻電路組合中的四個(gè)電阻R1、R2、R3和R4組成。電源電壓為V，電路中流動(dòng)的總電流為I。流過(guò)電阻R2和R3的電流為I1，流過(guò)電阻R4的電流為I2。

這里的電阻R2和R3串聯(lián)組合。因此，應(yīng)用串聯(lián)電阻規(guī)則，R2和R3的等效電阻為：

RA=R2+R3

這里RA是R2和R3的等效電阻

現(xiàn)在，電阻R2和R3可以用單個(gè)電阻RA代替。所得電路如下所示。

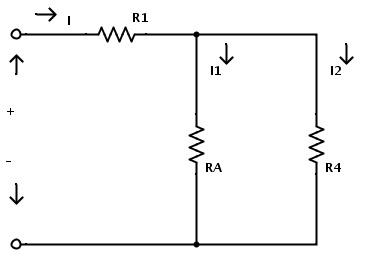
現(xiàn)在電阻RA和R4是并聯(lián)組合的。因此，通過(guò)應(yīng)用并聯(lián)組合電阻規(guī)則，RA和R4的等效電阻為

RB=RA×R4/(RA+R4)

這里RB是RA和R4的等效電阻

現(xiàn)在我們可以用單個(gè)電阻RB代替電阻RA和R4。更換電阻后，產(chǎn)生的電路如下所示。

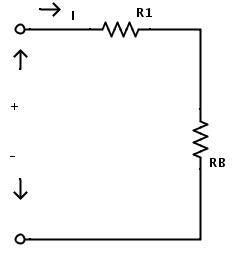
現(xiàn)在電路僅由兩個(gè)電阻組成。這里電阻R1和RB也是串聯(lián)組合的。因此，通過(guò)應(yīng)用串聯(lián)電阻規(guī)則，總電路等效電阻為

REQ=R1+RB

這里REQ是總電路等效電阻。現(xiàn)在電阻R1和RB可由單個(gè)電阻器代替REQ

上述復(fù)數(shù)電路的最終等效電路如下所示。

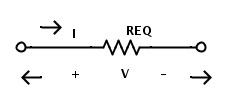
雖然它們看起來(lái)很復(fù)雜，但通過(guò)遵循串聯(lián)電阻和并聯(lián)電阻的簡(jiǎn)單規(guī)則，混合電阻電路可以簡(jiǎn)化為僅由一個(gè)電壓源和一個(gè)電阻組成的簡(jiǎn)單電路。

串聯(lián)和并聯(lián)電阻器示例

讓我們計(jì)算以下電路的等效電阻，該電路由7個(gè)電阻組成：R1=4Ω、R2=4Ω、R3=8Ω、R4=10Ω、R5=4Ω、R6=2Ω和R7=2Ω。電源電壓為5V。

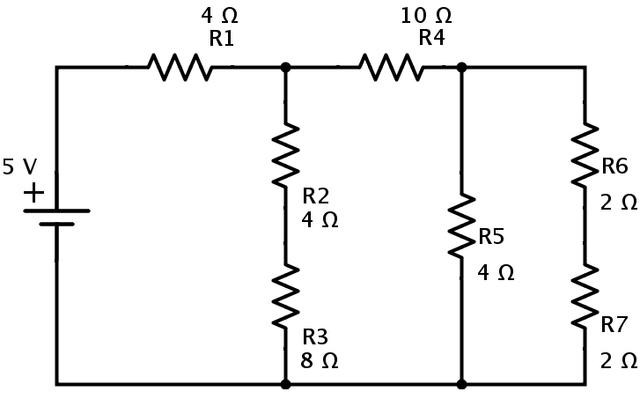
現(xiàn)在電阻R6和R7串聯(lián)組合。如果R6和R7in系列的等效電阻為Ra，則

Ra=R6+R7=2+2=4Ω

由此產(chǎn)生的電路簡(jiǎn)化為如下所示的電路。

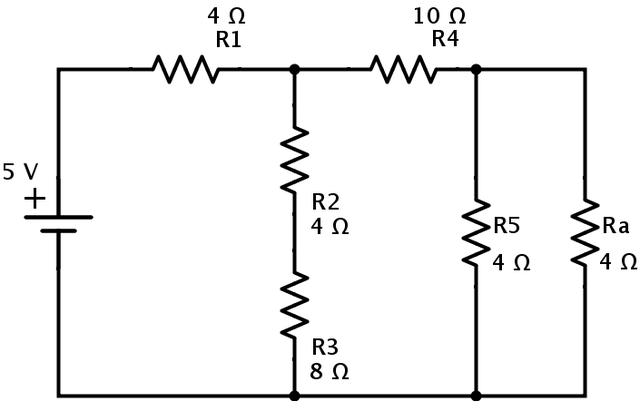
在上述電路中，電阻Ra和R5是并聯(lián)組合的。因此，Ra和R5的等效電阻為

Rb=(Ra×R5)/(Ra+R5)=(4×4)/(4+4)=2?.

然后簡(jiǎn)化電路如下所示。

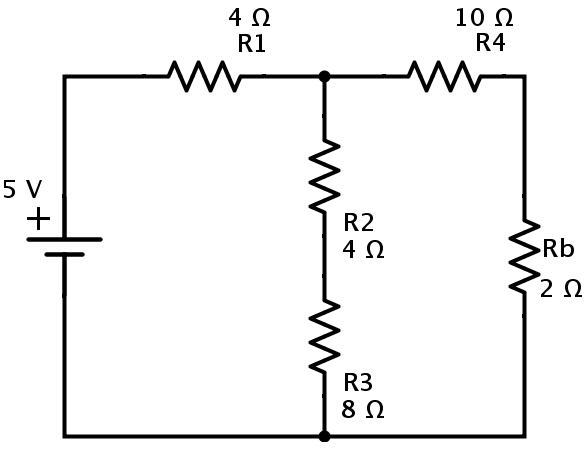
在該電路中，電阻R4和Rb是串聯(lián)組合。

Rc=R4+Rb=10+2=12?.

現(xiàn)在我們可以更換電阻R4和R。b電阻Rc如下所示。

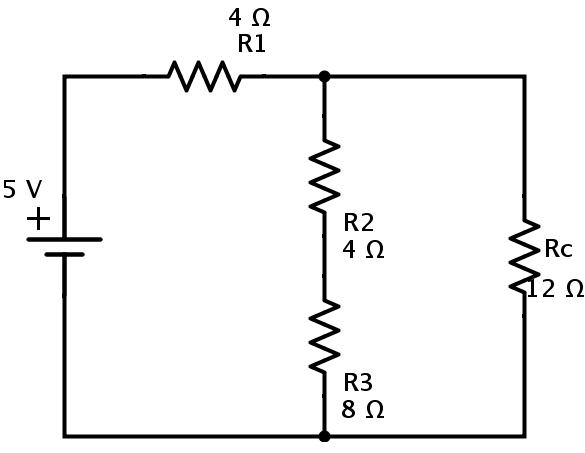
在上述電路中，電阻R2和R3再次串聯(lián)組合。如果Rd是R2和R3的等效電阻，則

Rd=R2+R3=4+8=12Ω。

等效電路為

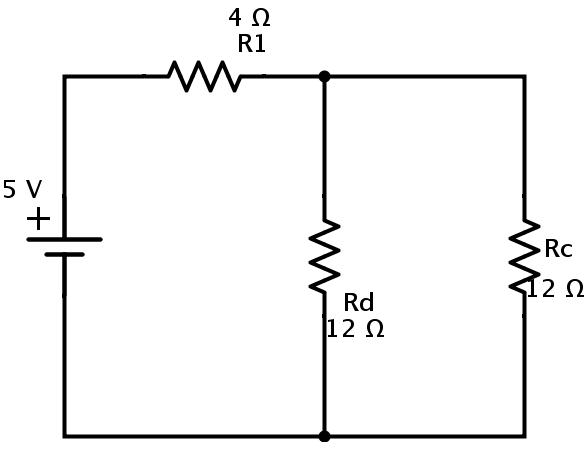
此處電阻Rc和Rd是并聯(lián)組合的。設(shè)Rp是并聯(lián)Rc和Rd的等效電阻。然后

Rp=(Rc×Rd)/(Rc+Rd)=(12×12)/(12+12)=6?.

得到的電路是

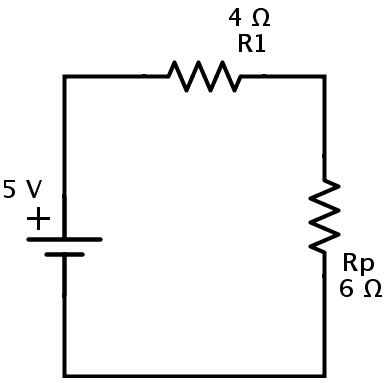
這里，電阻R1和Rp串聯(lián)組合。讓R情商是此組合的等效電阻。

然后

REQ=R1+Rp=4+6=10?.

這是電路的等效電阻。因此，給定的電路最終可以重新繪制為

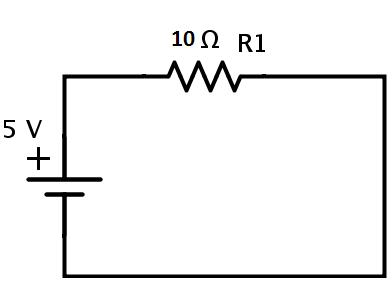
電路中的電流可以根據(jù)歐姆定律計(jì)算

I=V/REQ=5/10=0.5A

電阻器網(wǎng)絡(luò)

我們來(lái)計(jì)算復(fù)雜電阻電路的等效電阻。

以下電路由十個(gè)電阻R1至R10組成，它們以串聯(lián)和并聯(lián)方式連接。

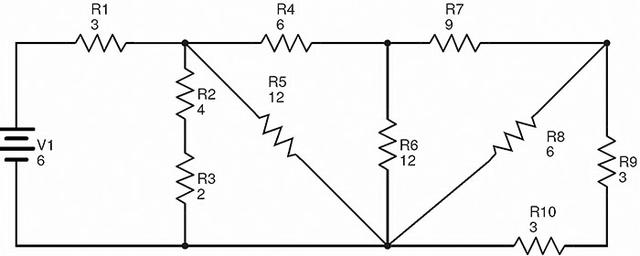
電路中提到的電阻值以歐姆（Ω）為單位，電源電壓以伏特（V）為單位。

此處電阻R9和R10串聯(lián)組合。讓RA是此組合的等效電阻。

因此RA=R9+R10=3+3=6?.

用R替換R9和R10后的電路A是

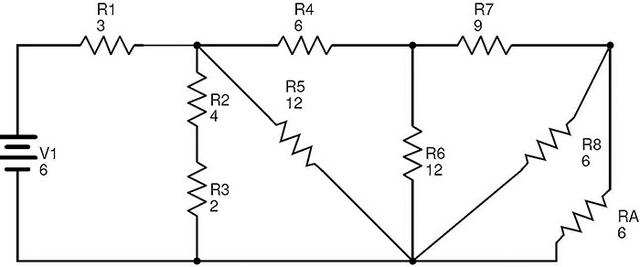
在該電路中，電阻R8和RA是并行組合的。那么R8和R的等效電阻A是

RB=(R8×RA)/(R8+RA)=(6×6)/(6+6)=3?.

現(xiàn)在取代R8和RA與RB，我們得到以下電路。

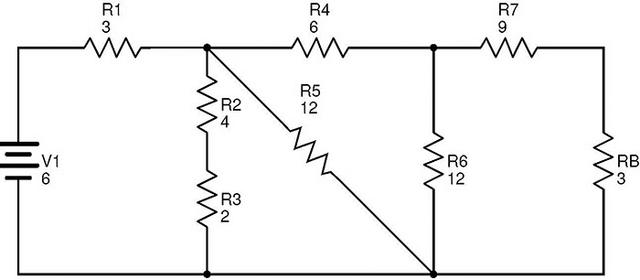
在該電路中，電阻R7和RB是串聯(lián)組合。

RC=R7+RB=9+3=12?.

更換R7和R后的等效電路B與RC是

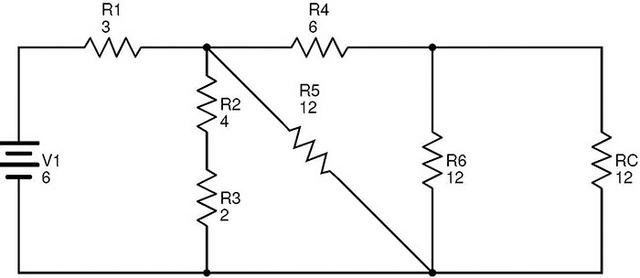
很明顯，電阻R6和Rc是并聯(lián)組合的。如果RD是這個(gè)組合的等效電阻，那么

RD=(R6×Rc)/(R6+Rc)=(12×12)/(12+12)=6?.

R?D取代R6和Rc的電路是

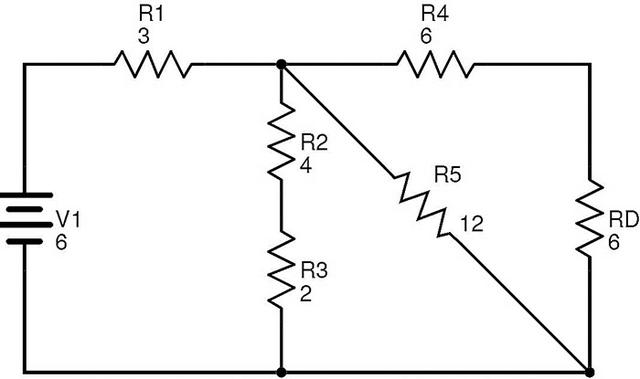
現(xiàn)在電阻R4和RD串聯(lián)組合。如果RE是R4和RD的等效電阻，則

RE=R4+RD=6+6=12?.

更換R4和R后產(chǎn)生的電路減少D與RE是

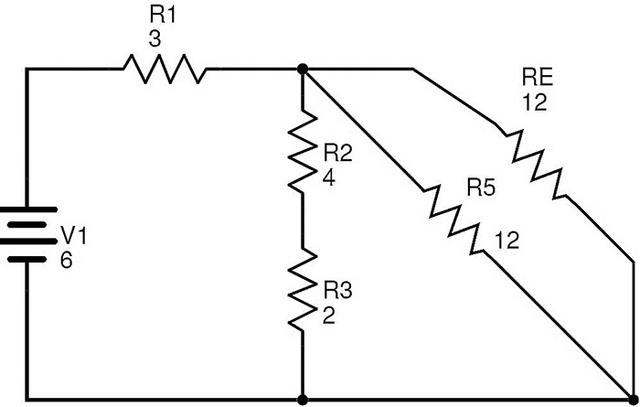
在該電路中，電阻R5和RE是并行組合的。

讓RF是R5和R的等效電阻E并行。

RF=(R5×RE)/(R5+RE)=(12×12)/(12+12)=6?.

簡(jiǎn)化電路如下所示。

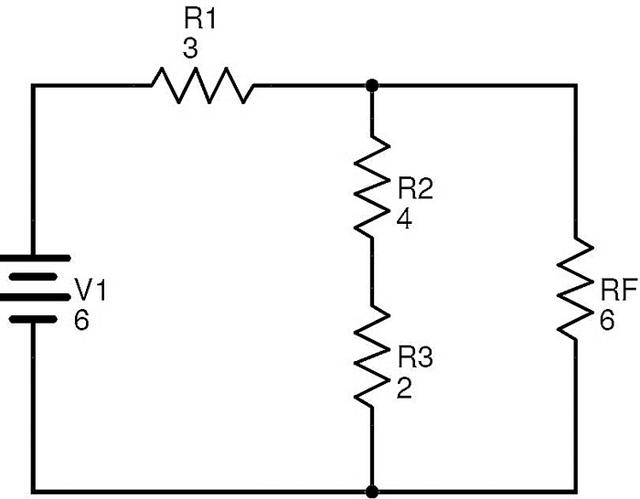
此處電阻R2和R3串聯(lián)。如果RG等效于此組合，則

RG=R2+R3=4+2=6Ω。

用RG替換R2和R3后，電路將轉(zhuǎn)換為

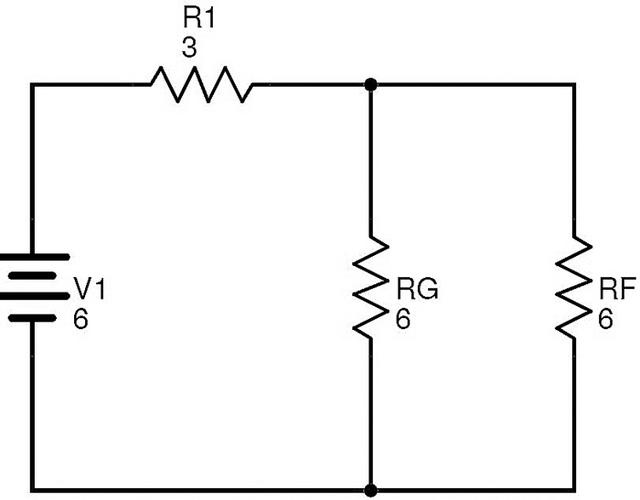
電阻RF和RG并聯(lián)。

讓RT等效于此組合。

然后RT=(RF×RG)/(RF+RG)=(6×6)/(6+6)=3?.

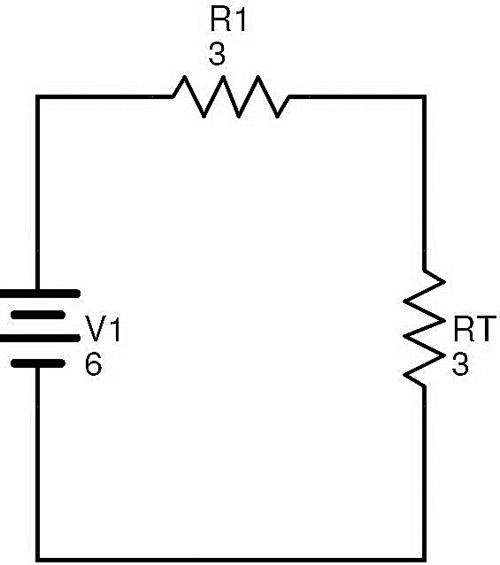
現(xiàn)在電阻R1和RT串聯(lián)。如果REQ是總電路等效電阻，則REQ=R1+RT=3+3=6Ω。

最后可以按如下方式重繪上述復(fù)雜電路

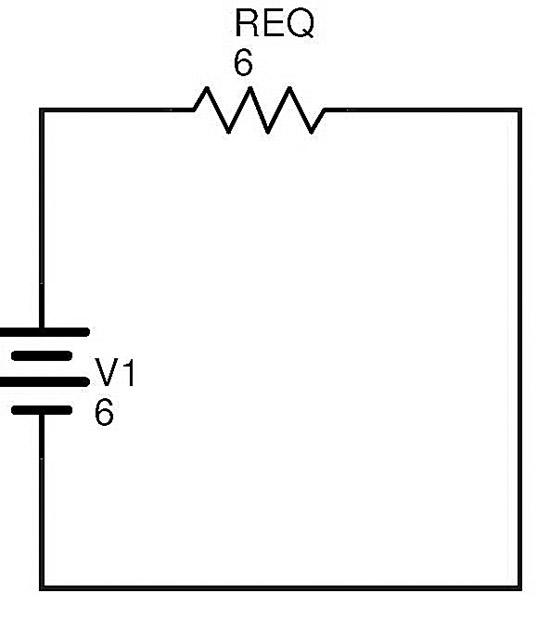
電路中的總電流可以使用歐姆定律計(jì)算

I=V1/REQ=6/6=1A

因此，通過(guò)首先識(shí)別簡(jiǎn)單的并聯(lián)電阻支路和串聯(lián)電阻支路，可以減少由串聯(lián)和并聯(lián)組合連接的電阻器數(shù)量組成的復(fù)雜電阻電路。計(jì)算這些簡(jiǎn)單分支的等效電阻，并將分支替換為等效電阻。這個(gè)過(guò)程降低了電路的復(fù)雜性。通過(guò)繼續(xù)這個(gè)過(guò)程，我們可以用單個(gè)電阻器代替復(fù)雜的電阻電路。

有一些復(fù)雜的電阻電路不能通過(guò)簡(jiǎn)單地應(yīng)用串聯(lián)電阻組合和并聯(lián)電阻組合的規(guī)則來(lái)簡(jiǎn)化為簡(jiǎn)單電路。T-Pad衰減器和一些復(fù)雜的電阻橋網(wǎng)絡(luò)等電路就是這種復(fù)雜電阻電路的例子。為了簡(jiǎn)化這些復(fù)雜的電阻電路，需要采用不同的方法。

一些復(fù)雜的電阻電路可以通過(guò)使用基爾霍夫電流定律和基爾霍夫電壓定律來(lái)減少。

僅使用歐姆定律來(lái)找到復(fù)雜電阻電路中的電流和電壓可能是不可能的。對(duì)于這種類型的電路，基爾霍夫電路定律將有所幫助。

基爾霍夫電路定律基于電路中電流和能量守恒的概念。有兩個(gè)基爾霍夫巡回定律。第一個(gè)是基爾霍夫電流定律，它處理節(jié)點(diǎn)上的電流，第二個(gè)是基爾霍夫電壓定律，它處理閉合電路中的電壓。

基爾霍夫電流定律指出：“進(jìn)入節(jié)點(diǎn)的電流等于離開(kāi)節(jié)點(diǎn)的電流，因?yàn)樗鼪](méi)有其他地方可去，節(jié)點(diǎn)中也沒(méi)有電流丟失。

簡(jiǎn)而言之，基爾霍夫電流定律指出，進(jìn)入節(jié)點(diǎn)的電流總和等于離開(kāi)電路的電流總和。

基爾霍夫電壓定律指出，“閉環(huán)中的總電壓等于該回路中所有電壓降的總和。

簡(jiǎn)單來(lái)說(shuō)，基爾霍夫電壓定律指出閉環(huán)中電壓的有向代數(shù)和等于零。

借助這兩個(gè)定律，可以計(jì)算出任何復(fù)雜電路中的電流和電壓值。

我們可能仍然有一些復(fù)雜的電阻電路，其中很難識(shí)別等效電阻，在這種情況下，我們將使用電阻器的星三角變換來(lái)簡(jiǎn)化電阻網(wǎng)絡(luò)。