電容器的電容定義為電容器在其體內存儲最大電荷(Q)的能力。在這里,電荷以靜電能的形式存儲。電容以基本SI單位(即法拉)測量。這些單位可以以微法拉、納法拉、皮法拉或法拉為單位。電容的表達式由下式給出,
C = Q/V = εA/d = ε0 εr A/d
在上式中
C是電容,
Q是收費,
V是板之間的電位差,
A是板之間的面積,
d 是板之間的距離。
ε介電常數
ε0 介電常數自由空間
εr自由空間的相對介電常數
自電容
自電容特性與電容器有關,特別是與隔離導體有關。顧名思義,電容是隔離導體中的屬性,以將其電位差提高到一伏特。通常,普通導體將具有互電容。這也以 S.I 單位(即法拉)來衡量。
半徑為“R”的導電球的自電容由下式給出,
C=4π?o****R
下面給出了一些標準器件的自電容值。
- 對于半徑為 20 cm 的范德格拉夫發(fā)電機的頂板,自電容為 22.24 pF。
- 對于地球,自電容為710 uF
雜散電容
雜散電容是不需要的電容。電容器在電路中引入一些電容。但是電阻器,電感器,甚至電線等組件都會具有一些電容。這稱為雜散電容。通常在高頻下,這會給電路帶來噪聲。這種不需要的電容很小,除非導體在長距離或大面積內靠得很近。
雜散電容不能完全消除,但可以減少。電路設計人員在設計電路時應注意雜散電容。應保持元件和線路之間的距離,以減少不需要的電容。
它也以 S.I 單位測量,即法拉。
例如線圈匝數之間的電容,兩個相鄰導體之間的電容。
簡單系統(tǒng)的電容
電容的計算只不過是求解拉普拉斯定理?2φ = 0電容器表面具有恒定電位。下面給出了一些簡單系統(tǒng)的電容值和公式。

電容器上充電
電容器在其金屬板上存儲最大電荷 (Q) 的能力稱為其電容值 (C)。存儲電荷的極性可以是負極或正極。如電容器的一個板上的正電荷(+ve)和另一個板上的負電荷(-ve)。電荷、電容和電壓的表達式如下。
C = Q/V, Q = CV, V = Q/C
因此,電容器的電荷與其電容值和電容器極板之間的電位差成正比。電荷以庫侖為單位。
一庫侖:
電容器上的一庫侖電荷可以定義為兩個導體之間的一法拉電容,其工作電壓為一伏。
以空氣為電介質
存儲在具有電容C的電容器中的電荷“Q”,電位差“V”和空氣作為其電介質由下式給出,
Q =C V =(ε× (A ×V)) /d
以固體為電介質
具有固體作為電介質的電容器的電荷“Q”由下式給出,
Q =C V =(ε0 ×εr× (A ×V)) /d
這里
ε0是自由空間的介電常數,
εr是介電材料的相對介電常數,并且
ε是介電材料的介電常數。
從以上兩個案例我們可以觀察到
電容器的電荷與極板的面積、極板之間介電材料的介電常數成正比,并且與極板之間的間隔距離成反比。
因此,極板的面積越大,電荷越多,極板之間的間隔距離越小,電容器上的電荷越少。
平行板電容器

上圖為平行板電容電路。眾所周知,電容與板的面積(A)成正比,與兩塊金屬板之間的間隔距離(d)成反比。平行板電容器的電容值由下式給出,
C = k ε0A/d
這里k是介電常數,ε0是自由空間的介電常數,等于8.854 X 10 -12 F/m。介電常數(k)是與介電材料相關的參數,與空氣相比,它增加了電容。板的表面積越大是電容值越大,間隔距離越小是電容值越低。下圖顯示了平行板電容器電路的另一個示例。

電容示例No1
現(xiàn)在,我們將計算平行板電容器的電容(以皮法為單位),其板的表面積為200 cm2,它們之間的距離為0.4 cm,空氣作為其介電材料。
我們知道平行板電容器的電容公式為:
C = εA/d
這里 ε = 8.854 X 10-12F/m
A = 200 cm2 = 0.02 m2
D = 0.4 cm = 0.004m
現(xiàn)在我們在上面的等式中替換這些值,
C = 8.854 X 10-12 * (0.02 m2/0.004m) = 44.27 pF
此處,平行板電容器的電容為44.27 pF
電容器的充電和放電
以下電路用于說明電容器的充電和放電特性。讓我們假設電路中顯示的電容器已完全放電。在該電路中,電容值為100uF,施加到該電路的電源電壓為12V。
現(xiàn)在,連接到電路中電容器的開關移動到A點。然后電容器開始以充電電流(i)充電,并且該電容器也充滿電。
電容器兩端的充電電壓等于電容器完全充電時的電源電壓,即VS = VC = 12V。當電容器充滿電時,意味著即使電源電壓與電路斷開,電容器也能保持恒定電壓充電。
在理想電容器的情況下,電容器上的電荷保持不變,但在一般電容器的情況下,充滿電的電容器由于其漏電流而緩慢放電。
當開關移動到位置B時,電容器通過打開電路中連接的燈來緩慢放電。最后完全放電至零。當電容器充滿電時,燈最初會發(fā)出明亮的光,但隨著電容器中的電荷減少,燈的亮度會降低。

電容器充電示例No2
現(xiàn)在讓我們計算上面電路中電容器的電荷,我們知道,電容器的電荷方程為
Q = 簡歷
這里,C = 100uF
V = 12V
Q = 100uF * 12V = 1.2mC
因此,上述電路中電容器的電荷為1.2mC。
通過電容器的電流
流過任何電路的電流(i)是相對于時間流過它的電荷速率(Q)。但是電容器的電荷與通過它施加的電壓成正比。電容器的電荷、電流和電壓之間的關系如下式給出。
I (t) = d Q(t)/dt = C dV(t)/dt
我們知道
V = 問/C
V (t) = Q(t)/C
Q(t) =C V(t)
電流與電壓的關系由下式給出,I (t) = C dV(t)/dt
從這種關系中,我們觀察到流過電路中電容器的電流是電容和施加到電路的電壓變化率的乘積。流過電容器的電流與電容器的電容和電壓速率成正比。
電流越大,電路的電容越高,施加的電壓越高,流過電路的電流就越大。如果電壓恒定,則電荷也是恒定的。因此沒有電荷流。因此,流過電路的電流將變?yōu)榱恪?/p>
電容單位(法拉)
Josiah Latimer Clark在1861年首次使用Farad一詞。法拉是電容的標準單位。這是一個非常大的電容單位。
一法拉電容定義為具有一庫侖電荷的電容,其工作電壓為一伏特。
C = Q/V
1法拉 = 1Coluomb/1V
現(xiàn)在,電容器具有數百法拉的大電容值。這些具有高電容值的電容器被稱為“超級電容器”。這些電容器利用大表面積來提供高能量,因為它們具有高電容值。
在低電壓下,超級電容器能夠以高電容值存儲高能量。這些高能量超級電容器用于手持便攜式設備,以取代大型,重型和昂貴的鋰型電容器,因為它們存儲高能量,如電池。這些電容器還通過更換高電池用于車輛的音頻和視頻系統(tǒng)。
法拉的子單位
電容的標準單位是法拉。但這通常是測量電容的大單位。這個法拉有一些子單位;它們是微法拉(uF),納法拉(nF)和皮法拉(pF)。
所有這些亞單位與法拉之間的關系是
1微法拉 (uF) = (1/1000000) F = 10-6 F
1納法拉 (uF) = (1/1000000000) F = 10-9 F
1皮法拉 (uF) = (1/1000000000000) F = 10-12 F
現(xiàn)在我們將看到電容子單元之間的一些轉換,
(i) 將33pF轉換為nF => 33pF = 0.033nF
(ii) 將22nF轉換為uF => 22nF = 0.022uF
(iii) 將11uF轉換為F => 11uF = 0.11F
電容器中的能量
能量是針對靜電場使電容器完全充電的一些功量。在電容器充電的初始階段,電荷Q在極板之間從一個極板轉移到另一個極板。該電荷為+Q或-Q,在電容器的兩個極板之間互換。
一些電荷轉換后,板之間會形成電場,在這種情況下,我們需要一些額外的工作才能使電容器完全充電。這種額外的功稱為存儲在電容器中的能量。能量以焦耳 (J) 為單位測量。現(xiàn)在我們看到了這種能量和功的方程。
dW = V dQ
dW = (Q/C) dQ
上述等式積分后為,
W = Q2/2C
W = (CV)2/2C
W= CV2/2焦耳
最后,我們得到存儲在電容器中的能量是
能量 (W) = CV2/2焦耳
現(xiàn)在我們計算存儲在電容為 200 uF 的電容器中的能量,該電容器以 12V 的電壓工作。
W = CV2/2
W = (200×10-6×122)/2 = 14.4 米焦耳
-
電容器
+關注
關注
64文章
6205瀏覽量
99320 -
電感器
+關注
關注
20文章
2324瀏覽量
70413 -
存儲器
+關注
關注
38文章
7453瀏覽量
163608 -
電源電壓
+關注
關注
2文章
986瀏覽量
23944 -
電容充放電
+關注
關注
0文章
94瀏覽量
5829
發(fā)布評論請先 登錄
相關推薦
IGBT電壓與電荷分布之間的關系(1)
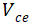




 電容和電荷之間有何關系?
電容和電荷之間有何關系?










評論