傅里葉變換的時移特性和頻移特性
傅里葉變換是一種將時域函數(shù)轉換為頻域函數(shù)的數(shù)學工具,是信號處理領域中的重要工具之一。在信號處理中,時移和頻移是常見的操作,傅里葉變換的時移和頻移特性對于處理信號非常有幫助。本文將詳細介紹傅里葉變換的時移特性和頻移特性。
一、時移特性
時移是一種將信號在時間軸上平移的操作。在時域上,信號f(t)在時間t0處向右平移t1,則平移后的信號為f(t-t0),即
f(t-t0) = f(t-t1-t0+t1)
在頻域上,時移的結果是相位的改變。具體來說,若將一個函數(shù)f(t)在時域上時移t0,則對應的頻域函數(shù)F(ω)在相位上將發(fā)生改變。
根據(jù)傅里葉變換的定義,可知其時移特性為:
設F(ω)為f(t)的傅里葉變換,對f(t-t0)進行傅里葉變換,則有
F(ω)exp(-jωt0)
公式中的exp(-jωt0)是時移的頻域表達式。可以看出,傅里葉變換的時移特性是一個相位的改變。
二、頻移特性
頻移指的是在頻域上進行的平移操作。假如對于信號f(t)進行了頻移操作,那么將f(t)在頻域上移動Δω,則平移后的頻域函數(shù)為
F(ω-Δω)
頻移特性的主要作用是用來分析在我們進行某些信號處理操作時,對信號的頻譜有什么影響,同時用于數(shù)字濾波器的設計過程中。
三、應用舉例
在信號處理中,時移和頻移特性是非常重要的概念,可以用于各種信號處理應用,如濾波、信號的儲存和重建等。
(1)信號濾波
在濾波中,我們經(jīng)常需要將信號在時域或者頻域上進行平移后再濾波。通過時移和頻移特性,我們可以快速地得到該信號在移動后的頻譜,并可以基于此來設計我們所需的濾波器。
(2)信號的儲存和重建
在數(shù)字信號的儲存與重建中,我們通常需要對信號進行采樣和重構。采樣過程相當于對原始信號進行時移操作,而重構過程則相當于對采樣后的信號進行頻移操作。通過傅里葉變換的時移和頻移特性,我們可以方便地進行信號的采樣和重構操作。
(3)信號的分析和合成
信號的分析和合成通常需要進行頻域的變化和轉換。通過傅里葉變換的時移和頻移特性,我們可以方便地對信號進行分析和合成處理,達到所需的效果。
四、總結
時移和頻移特性是傅里葉變換中重要的概念,其應用廣泛,具有很高的實用性。特別是在濾波、信號處理、信號的儲存和重建以及信號的分析和合成等方面,能夠為我們提供很多幫助和方便。因此,加深傅里葉變換的時移和頻移特性的理解將有助于更好地應用和理解信號處理中的相關問題。
-
傅里葉變換
+關注
關注
6文章
438瀏覽量
42566 -
信號濾波器
+關注
關注
0文章
20瀏覽量
3053
發(fā)布評論請先 登錄
相關推薦
傅里葉變換的基本性質和定理
經(jīng)典傅里葉變換與快速傅里葉變換的區(qū)別
移相全橋拓撲原理分析 移相全橋與LLC的區(qū)別

移相全橋移相角怎么控制
什么是移相網(wǎng)絡?移相網(wǎng)絡的電路結構
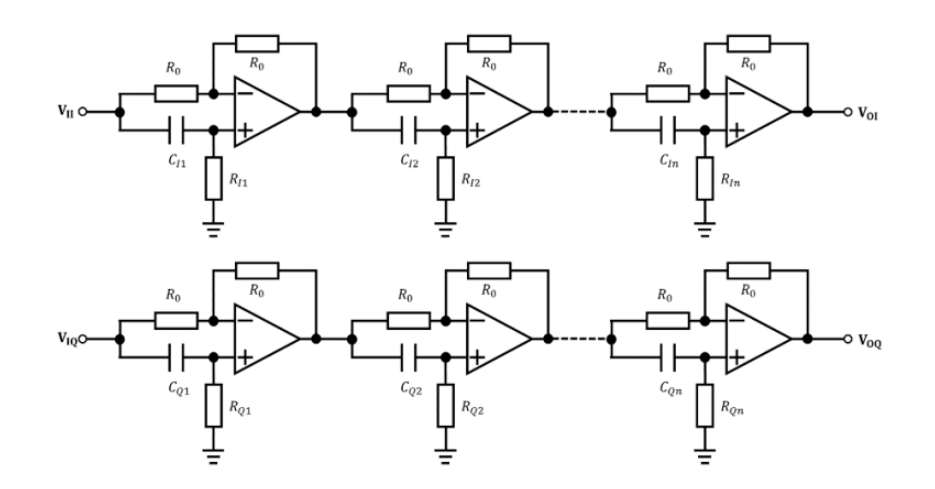
rc電路移相特性的觀察與分析
傅里葉變換的應用 傅里葉變換的性質公式
什么是傅里葉變換和逆變換?為什么要用傅里葉變換?
【實操】移相全橋DC-DC變換器快速設計與開發(fā)
移相全橋DC-DC變換器快速設計與開發(fā)





 傅里葉變換的時移特性和頻移特性
傅里葉變換的時移特性和頻移特性











評論