傅里葉變換與拉普拉斯變換的聯(lián)系解讀
傅里葉變換和拉普拉斯變換都是數(shù)學中非常重要的分析工具。它們都在不同的領域中發(fā)揮著重要作用。
傅里葉變換是一種將時間域信號轉換成頻率域信號的技術。它是通過將信號分解成不同頻率的正弦波成分來實現(xiàn)的。傅里葉變換能夠很容易地分析一個信號的頻率分布情況,并且在通信、圖像處理、音頻處理等應用中有廣泛的應用。傅里葉變換是通過將信號分解成不同頻率的正弦波成分來實現(xiàn)的。具體來說,傅里葉變換將一個信號f(x)分解成無限個正弦函數(shù)的加權線性組合:
F(ω) = ∫f(x)e^(-iωx)dx
其中F(ω)是信號的頻率域表示,e^(-iωx)是ω和x的函數(shù),ω表示頻率,x表示時間。這個式子可以讓我們根據(jù)f(x)的頻率域表示來確定它源自什么位置的諧波。
而拉普拉斯變換是一種將時間域信號轉換成頻率域信號的技術。它是通過對信號進行復頻域變換來實現(xiàn)的。拉普拉斯變換可以更簡單地處理“非恒定”信號。具體來說,它將一個時間域函數(shù)f(t)轉換成一個復頻域函數(shù)F(s),其中s是一個復變量:
F(s) = ∫f(t)e^(-st)dt
拉普拉斯變換將函數(shù)f(t)分解成無限個指數(shù)函數(shù)的加權線性組合,每個指數(shù)函數(shù)都有一個相關的加權系數(shù)。對于不同的函數(shù)f(t),拉普拉斯變換可以產(chǎn)生一個獨特且具有重要意義的復頻率域表示。
那么傅里葉變換和拉普拉斯變換之間有什么聯(lián)系呢?
事實上,傅里葉變換和拉普拉斯變換之間存在著緊密的聯(lián)系。它們之間最顯著的聯(lián)系在于,拉普拉斯變換是傅里葉變換在復平面上的推廣。
具體來講,我們可以將拉普拉斯變換看做是以復頻率的形式描述傅里葉變換。在傅里葉變換中,信號是通過對頻率的積分來描述的,而在拉普拉斯變換中,信號是通過對復變量s的積分來描述的。因此,拉普拉斯變換可以被認為是傅里葉變換的推廣。
此外,傅里葉變換和拉普拉斯變換都有類似于傅里葉級數(shù)的性質。傅里葉變換和拉普拉斯變換的一些性質包括:線性性、時移和頻移、對稱性等等。這些性質使得傅里葉變換和拉普拉斯變換非常有用,并使它們可以在許多不同的領域中被廣泛地使用。
總之,傅里葉變換和拉普拉斯變換是數(shù)學中重要的分析工具,在信號處理、控制系統(tǒng)、通信等領域有著廣泛的應用。雖然它們與彼此都有其獨特性質,但它們之間也存在著緊密的聯(lián)系。深入地研究這些變換將使我們更好地理解信號和系統(tǒng)的行為,并為我們提供在現(xiàn)實世界中解決問題的工具。
-
控制系統(tǒng)
+關注
關注
41文章
6550瀏覽量
110498 -
傅里葉變換
+關注
關注
6文章
438瀏覽量
42566 -
拉普拉斯變換
+關注
關注
1文章
31瀏覽量
10149
發(fā)布評論請先 登錄
相關推薦
傅里葉變換的基本性質和定理
經(jīng)典傅里葉變換與快速傅里葉變換的區(qū)別
先進產(chǎn)能設備提供商拉普拉斯科創(chuàng)板上市
拉普拉斯變換的作用及意義
數(shù)字信號處理三大變換關系包括什么
Intersolar 2024丨慕尼黑,拉普拉斯來了!
拉普拉斯IPO:科技與產(chǎn)業(yè)深度融合,實現(xiàn)業(yè)務領域延展
證監(jiān)會同意拉普拉斯上交所科創(chuàng)板IPO注冊
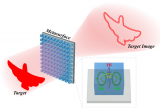
基于超構表面的拉普拉斯光學微分處理器可用于光學成像
拉普拉斯科創(chuàng)板IPO過會
傅里葉變換和拉普拉斯變換的關系是什么
傅里葉變換的應用 傅里葉變換的性質公式
什么是傅里葉變換和逆變換?為什么要用傅里葉變換?
短時傅里葉變換STFT原理詳解





 傅里葉變換與拉普拉斯變換的聯(lián)系解讀
傅里葉變換與拉普拉斯變換的聯(lián)系解讀










評論