繞組是電和磁的橋梁。匝鏈繞組的磁鏈發生變化時,繞組中就會產生感應電勢;給繞組通以電流時,就會產生磁勢。關于電機繞組的感應電勢相關內容,在前面幾期中已經詳細論述,本期開始講電機繞組的磁勢。
由于整數槽繞組的磁勢分布比較簡單,分數槽繞組的磁勢分布比較復雜。本著由淺入深、由簡到繁的原則,首先分析整數槽繞組的磁勢,再分析分數槽繞組的磁勢。在分析整數槽繞組的磁勢時,首先從單個整距線圈的磁勢入手,進而分析多個整距線圈組的磁勢和短距線圈組的磁勢,從而得出單相繞組的磁勢,最終得出三相繞組的合成磁勢以及繞組磁勢的諧波。分析完三相整數槽繞組和分數槽繞組的磁勢,最后討論多相(相數m>3)繞組的磁勢以及變極調速的原理。由于內容較多,我們將分多期進行講解。本期主要講單相整數槽繞組的磁勢。為了分析簡化,做以下假設:①假設槽內電流集中在槽中心處;②假設鐵心的磁導率為無窮大,所有磁勢都降落在氣隙中。
1 單個整距線圈的磁勢
繞組都是由許多個線圈連接而成,要想分析繞組的磁勢,必須從單個線圈的磁勢入手。如圖1a為一臺兩極電機的示意圖,定子中只有一個整距線圈,設整距線圈的匝數(每槽導體數)為Nc。
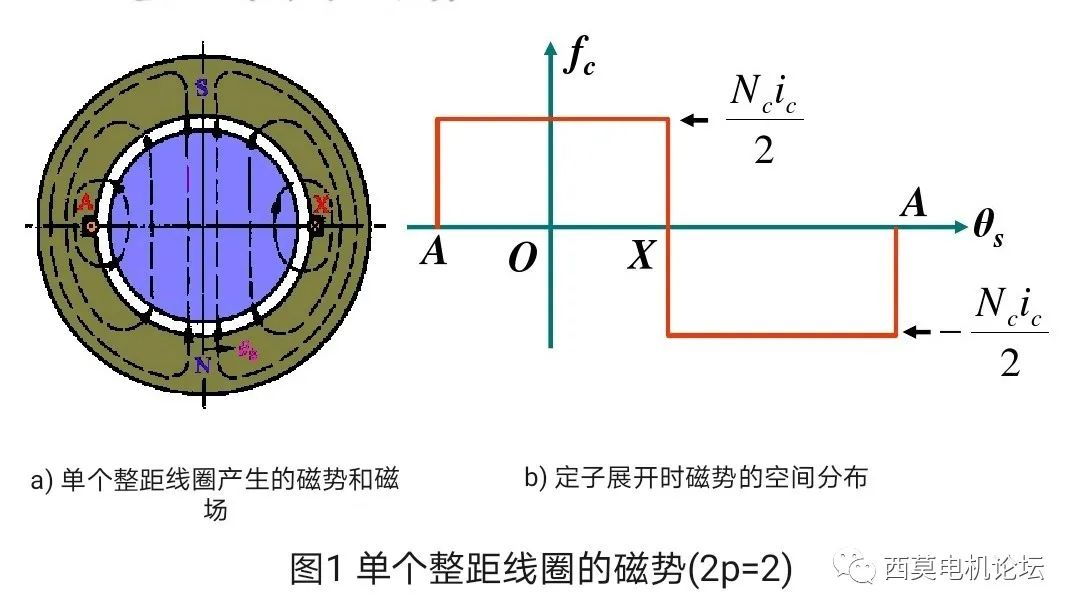
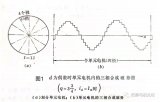
當線圈中通以交流電流ic時,例如某一時刻從X流入,從A流出,則這個線圈產生的磁勢即為其安匝數Nc?ic,在該磁勢作用下,線圈將產生一個兩極磁場,如圖1a)所示,定子內圓下端為N極,上端為S極。由于整距線圈相對于線圈軸線對稱,且相對于線圈平面上下也是對稱的,因此在假設鐵心的磁導率為無窮大的情況下,該磁勢被平均分配到上下半部分氣隙中,每個氣隙得到的磁勢即為總磁勢的一半,即Nc?ic/2,定義N極磁勢為正,S極磁勢為負,若以線圈的軸線處為原點,將氣隙圓周展開,即得到圖1b)所示的磁勢分布。由圖可見,由于假設槽內電流集中在槽中心處,則磁勢在經過一個線圈邊時將發生Nc?ic的跳變,因此一個整距線圈的磁勢沿氣隙在空間的分布是一個矩形波,矩形波的幅值為Nc?ic/2。該磁勢的空間分布表達式為:
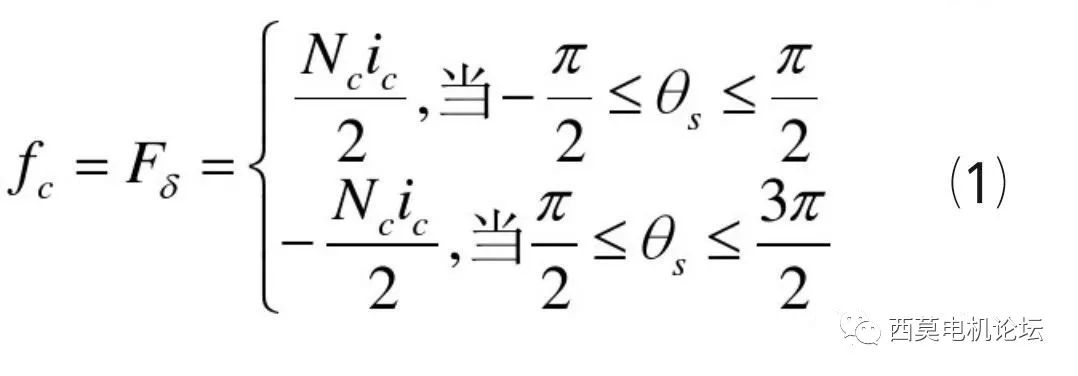
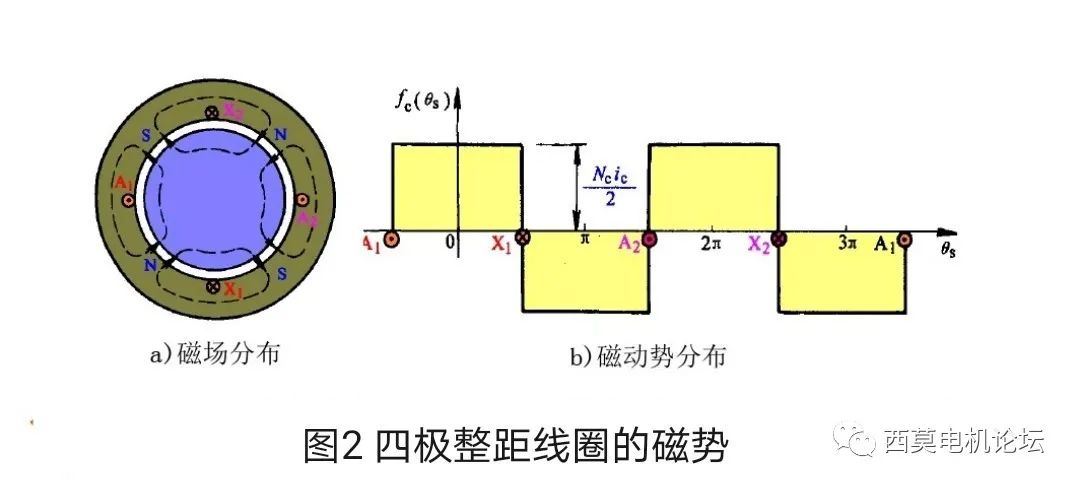
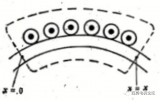
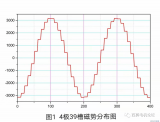
以上分析的是一對極的情況,對于整數槽多極電機,由于各對極下的磁勢分布情況均為一對極的重復,因此只需分析一對極即可,此時多極整距線圈產生的磁勢在空間的分布仍為矩形波,矩形波的幅值仍為Nc?ic/2,只不過是波長(2τ)不是兩極電機那樣為整個氣隙圓周周長,而是變為了1/p的氣隙周長。如圖2所示為四極整距線圈的磁場和磁勢分布情況。
如果線圈內所通的電流為直流電流,則矩形波的幅值就是Nc?ic/2固定不變的;若線圈內所通的電流為隨時間按余弦規律變化的交流電流,即:
ic=2^??Ic?cosωt (2)
則單個整距線圈產生的磁勢在空間上的分布仍然是矩形波,但矩形波的幅值則隨時間按余弦規律變化,即矩形波的幅值為:
fc(t)=Fcm?cosωt (3)
其中矩形波幅值的最大值為:
Fcm=(1/2^?)?Ic?Nc(4)
式中:Ic為線圈內交流電流的有效值。
當線圈內電流達到最大值2^??Ic時,矩形波磁勢幅值達到最大值Fcm;隨著電流瞬時值的減小,磁勢的幅值也將隨之減小,當電流減小到0時,整個空間的磁勢也變為0;當電流變為負值時,磁勢也隨之改變方向,電流達到負的最大值-2^??Ic時,矩形波磁勢幅值也達到負的最大值-Fcm。這種從空間上看,軸線位置固定不動,從時間上看,其大小不斷地隨著電流的交變而在正、負最大值之間脈振變化的磁勢(磁場),叫做“脈振磁勢(磁場)”,物理上也稱為“駐波”。脈振的頻率顯然與交流電流的頻率相同。
這里特別要重復強調的是,一定要把磁勢的空間分布規律和隨時間變化的規律區別清楚。空間分布用空間位置角度θ的函數來表達,整距線圈磁勢的空間分布是一個矩形波,若線圈內所通電流不變,則矩形波的幅值也不變,表達式見式⑴;磁勢隨時間變化的規律用時間t的函數來表示,若線圈中的電流隨時間按余弦規律變化,則沿定子內圓分布的矩形磁勢波幅值大小也將隨時間按余弦規律變化,其表達式如式⑶所示。
為了便于分析計算,常用諧波分析法對這個矩形波沿空間進行傅立葉分解,再次強調是沿空間進行傅立葉分解!得到矩形波沿空間的基波和各次諧波。如圖3所示。
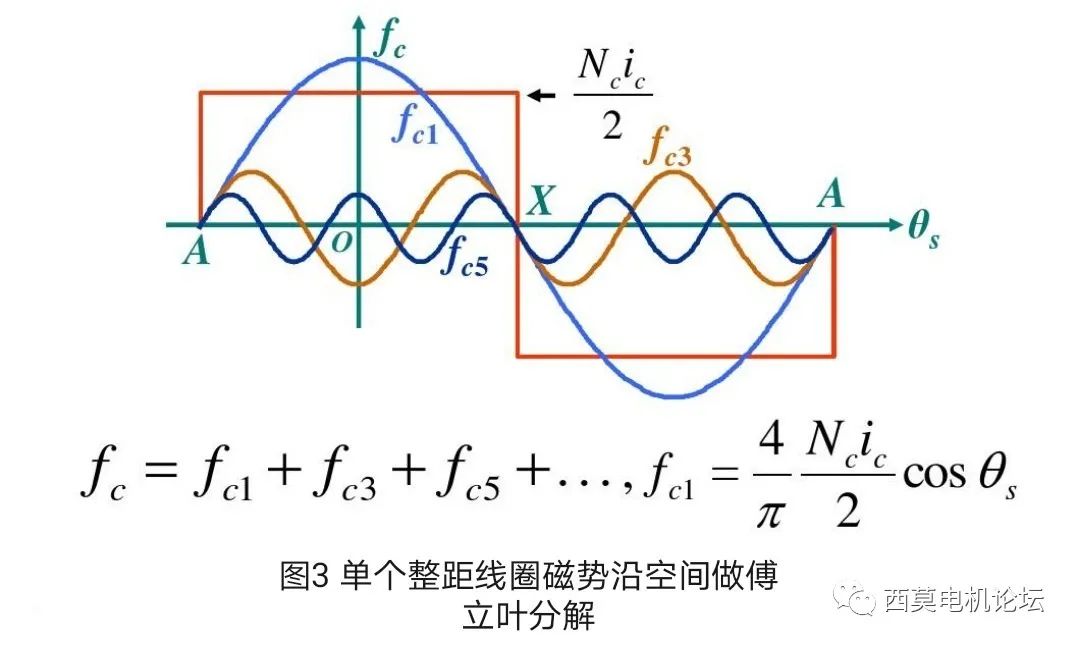
由圖3可見,由于整距線圈產生的矩形波磁勢是一個奇諧函數,因此將其做傅立葉分解后,只含有奇次諧波,而不含有偶次諧波。分解后磁勢表達式為:
fc(θ,t)=fc1?cosθ+fc3?cos3θ+fc5?cos5θ+fc7?cos7θ+… (5)
其中基波磁勢的極對數為p,基波磁勢的幅值為:
fc1=(4/π)Fcm?cosωt=Fcm1?cosωt (6)
υ次諧波磁勢的極對數為υp,幅值為:
fcυ=±(1/υ)?Fcm1?cosωt=±Fcmυ?cosωt (7)
上式中:Fcm1=(4/π)Fcm,為基波磁勢幅值的最大值;Fcmυ=(1/υ)Fcm1,為υ次諧波磁勢幅值的最大值;當υ=4k+1時取“+”號,當υ=4k-1時取“-”號,k=1,2,3…。
綜合以上各式,得單個整距線圈產生的磁勢時空表達式為:
fc(θ,t)=Fcm1?cosθ?cosωt
-(1/3)?Fcm1?cos3θ?cosωt
+(1/5)?Fcm1?cos5θ?cosωt
-(1/7)?Fcm1?cos7θ?cosωt
=Fcm1?[cosθ-(1/3)cos3θ+(1/5)cos5θ-(1/7)cos7θ+…]?cosωt (8)
由⑻式可以得到以下結論:
①單個整距線圈通以余弦(正弦)交流電流時,會產生一個脈振磁勢,它既是空間θ的函數又是時間t的函數。即這個脈振磁勢是沿空間相對于線圈軸線對稱的矩形波,矩形波的幅值大小又隨時間t按余弦(正弦)規律變化,變化頻率與電流頻率相等。
②把這個矩形波磁勢沿空間做傅立葉分解后,只含有奇次諧波,諧波磁勢幅值的大小與諧波次數成反比,諧波次數越高,幅值越小。
③基波和諧波的波峰(波谷)在線圈的軸線位置,取“+”號時為波峰;取“-”號時為波谷。
2 整距分布繞組的基波磁勢
幾個線圈串聯組成一個線圈組,也稱極相組。線圈組的磁勢應該就是各單個線圈磁勢的疊加。由于各線圈分布在氣隙圓周上,相鄰線圈之間在空間上錯開了一定的角度α(通常是槽距角),因此各線圈磁勢的疊加應該是矢量的疊加。如圖4所示為一個由q=3的整距線圈組成的極相組,極相組的三個線圈依次分布在三個相鄰的槽內,所以稱此繞組為整距分布繞組。
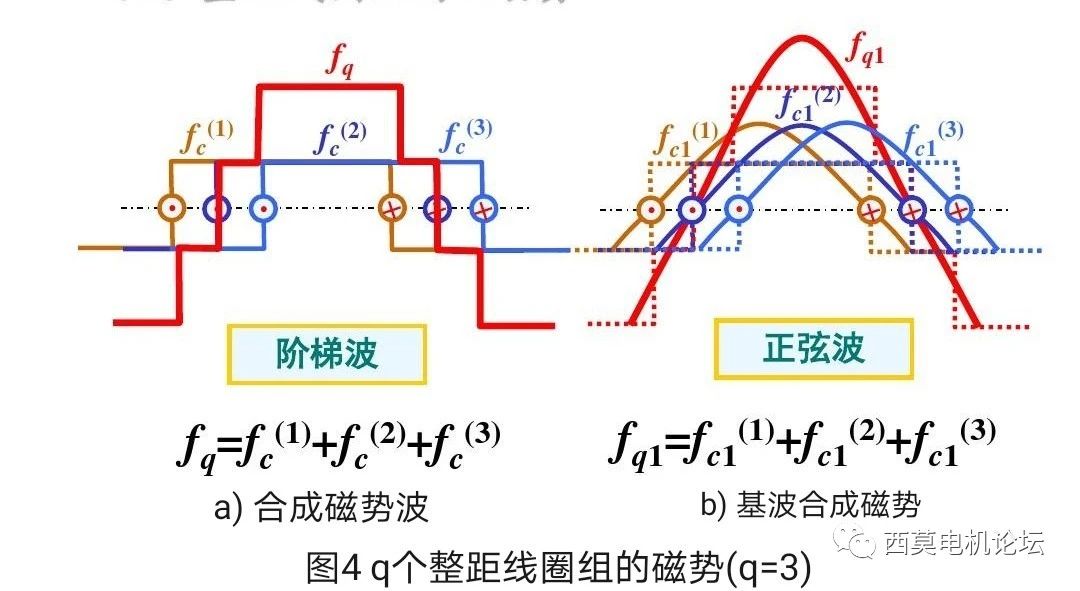
每個整距線圈產生的磁勢都是一個矩形波。由于每個整距線圈的匝數相等,且由于各線圈串聯,通過的電流也相等,故各線圈的矩形波磁勢幅值相等;由于線圈是分布的,相鄰線圈在空間上間隔α角,所以各線圈的矩形波磁勢在空間上亦相隔α電角度。把這三個線圈分別產生的矩形波磁勢逐點相加,即可得到整個極相組的磁勢波,如圖4a)所示。由圖可見極相組的合成磁勢為一個階梯波。將各單個整距線圈產生的矩形波磁勢做空間傅立葉分解,得到各單個線圈磁勢的基波和一系列高次諧波。這里我們先分析磁勢基波,磁勢諧波將在后續分析。圖4b)即為三個整距線圈的基波磁勢,其幅值相等、空間各相差α電角度。將這三個線圈的基波磁勢逐點相加,即可得到整個極相組的合成基波磁勢。由于基波磁勢在空間按余弦規律分布,故可以用空間矢量表示和運算,于是q個線圈的基波合成磁勢矢量就等于各線圈基波磁勢矢量的矢量和,如圖5所示。
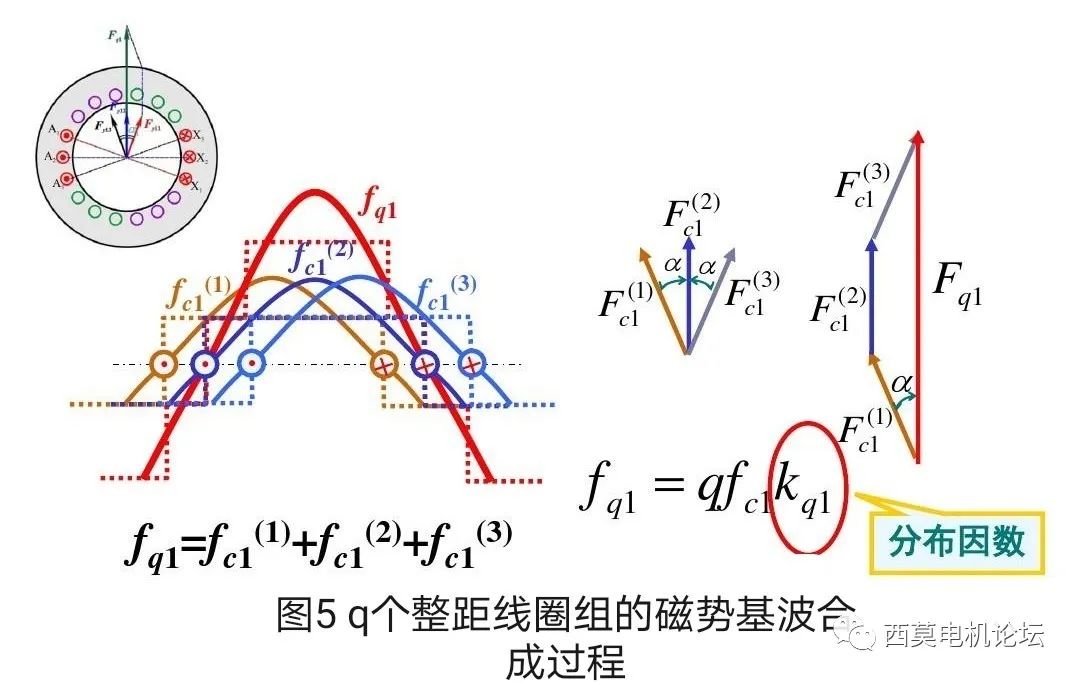
由圖5不難看出,利用矢量運算時,分布線圈基波磁勢的合成與前面所講的基波電勢的合成完全相似,因此同樣可以引入分布系數(或分布因數)Kd1來計及線圈分布的影響,即q個分布線圈產生的合成基波磁勢等于直接將q個線圈的基波磁勢算術相加基礎上,打一個分布因數Kd1的折扣。于是q個整距分布線圈組成的極相組的合成磁勢基波為:
fq1(θ,t)=q?fc1?Kd1?cosθ
=(4/π)?(1/2^?)?Ic?q?Nc?Kd1?cosθ?cosωt (9)
3 短距分布繞組的基波磁勢
以上分析了整距線圈及整距分布繞組的基波磁勢,接下來分析短距分布繞組的基波磁勢。如圖6所示為q=2、線圈節距y1=5(極距τ=6)的雙層短距分布繞組,一對極下屬于同一相有兩個極相組。按照短距繞組的連接規律,應該是第1、2槽上層邊分別與第6、7槽下層邊連接構成一個極相組;第7、8槽上層邊分別與12、13槽的下層邊連接構成另一個極相組。由于在鐵心有效長度內,磁勢的大小和波形僅僅取決于槽內有效邊的分布情況以及導體內的電流,而與線圈端部的連接次序無關,因此,為了簡化分析,可以把兩個短距極相組的上層邊視為一組q=2的整距分布繞組;把兩個短距極相組的下層邊視為另一組q=2的整距分布繞組;這兩組整距分布繞組在空間上錯開ε電角度。這樣得到的磁勢分布與兩個短距分布繞組的磁勢分布是完全一樣的。其中ε角恰好等于短距線圈的節距比整距時縮短的電角度,即ε=180o?(τ-y1)/τ。
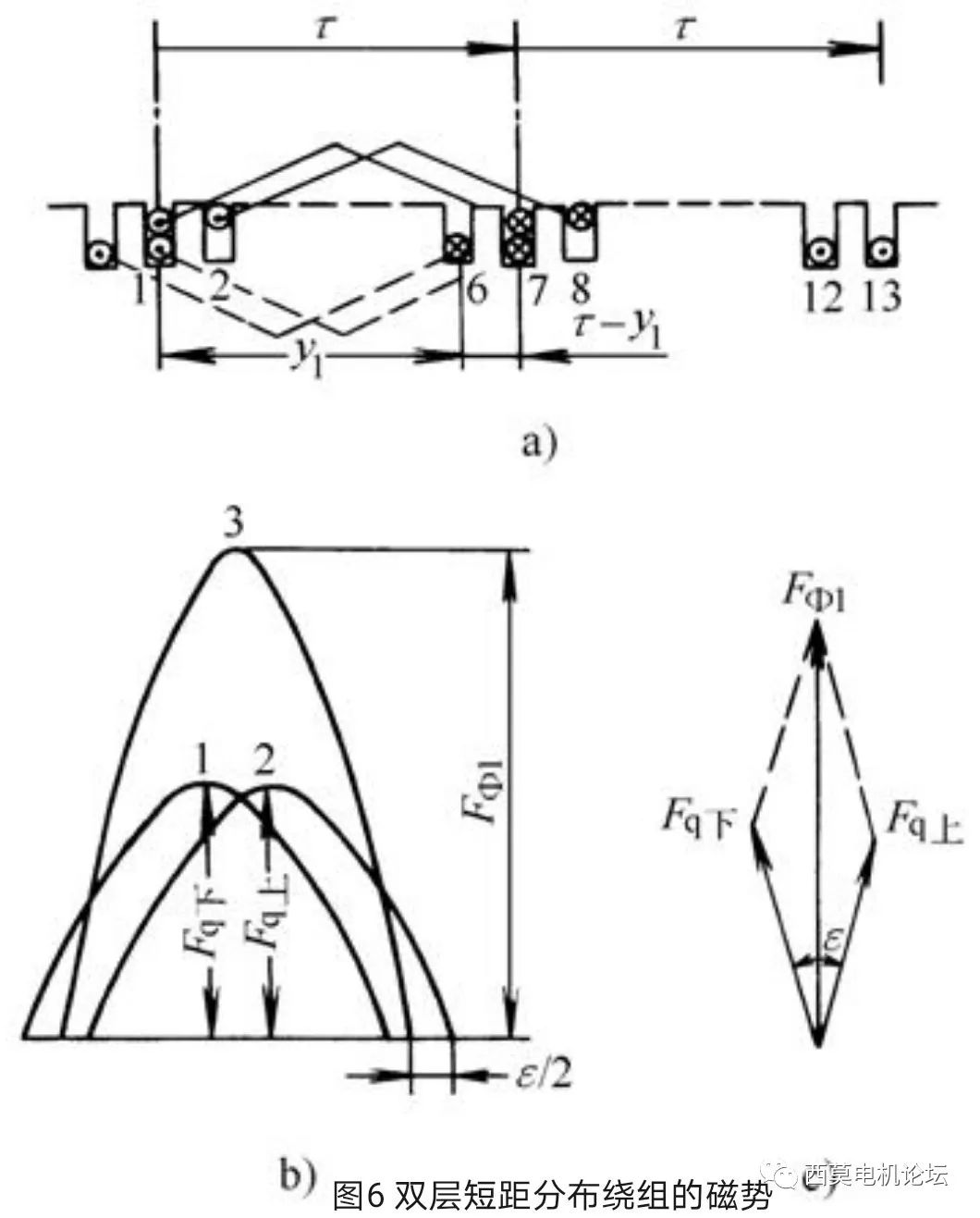
圖6b)表示兩條分別代表上下層整距分布繞組基波磁勢的正弦曲線逐點相加,得到雙層短距分布繞組的基波磁勢;圖6c)為對應的基波磁勢空間矢量相加過程。不難看出,雙層短距分布繞組的基波磁勢是雙層整距時的cos(ε/2)倍,而這個系數cos(ε/2)=sin(90o?y1/τ)=Kp1,也就是說,計及短距時,繞組的磁勢基波引入的系數恰恰是計算短距繞組電勢基波時引入的短距系數。于是,雙層短距分布繞組的基波磁勢為:
fq1(θ,t)=2q?fc1?Kd1?Kp1?cosθ
=(4/π)?2^??Ic?q?Nc?Kdp1?cosθ?cosωt (10)
其中:Kdp1=Kd1?Kp1為基波繞組系數,與電勢的基波繞組系數相同。
4 單相繞組的基波磁勢
由于各對極下的磁勢和磁阻組成一個對稱的分支磁路,因此一相繞組產生的磁勢就等于一對極下的磁勢,也就是⑽式所示的磁勢也就是單相繞組的磁勢。考慮到⑽式中的電流Ic為極相組中導體內的電流有效值;Nc為極相組中每個線圈的匝數(對于單層繞組為每槽導體數;對于雙層繞組為每半槽導體數),而單相繞組的磁勢應該體現與相電流和每相串聯匝數的關系。因此需要將⑽式中的電流IC和線圈匝數分別用相電流和每相串聯匝數予以替換。由于雙層繞組的每相串聯匝數W=q?2p?Nc/a,其中a為并聯支路數;相電流IΦ=a?Ic,將此關系代入⑽式,得每相繞組的基波磁勢為:
fΦ1(θ,t)=(4/π)?2^??(W?Kdp1/2p)?IΦ?cosθ?cosωt=FΦ1?cosθ?cosωt (11)
其中FΦ1為單相繞組的基波磁勢幅值。
FΦ1=(4/π)?2^??(W?Kdp1/2p)?IΦ=0.9?(W?Kdp1/p)?IΦ (12)
以上兩式中:W為每相串聯匝數,IΦ為相電流有效值。需要說明一下,雖然以上兩式是在雙層繞組基礎上推導出來的,但無論是單層繞組還是雙層繞組,以上兩式都適用。
由以上兩式可知:
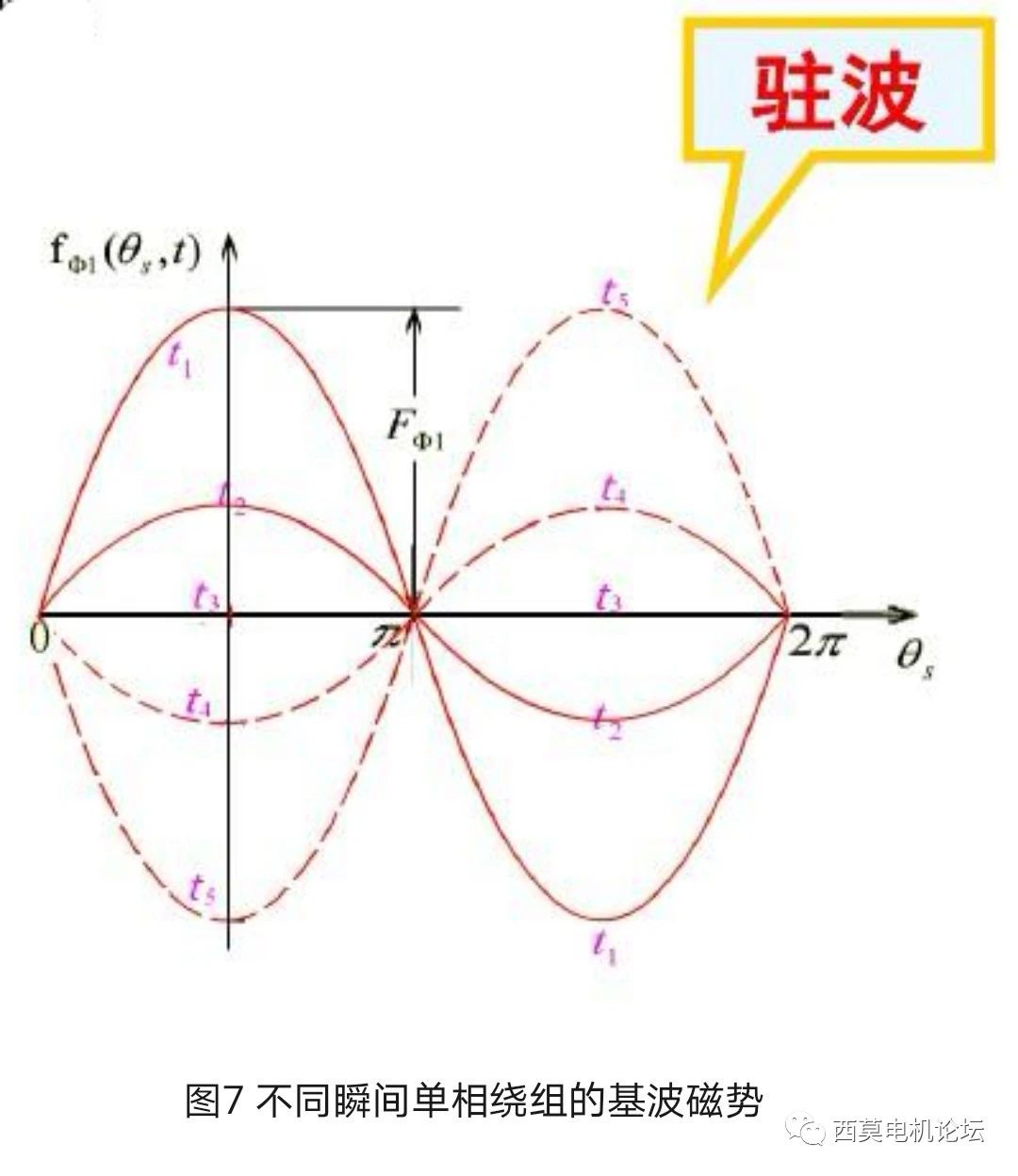
①當單相繞組中通以余弦(正弦)交流電流時,產生的基波磁勢為脈振磁勢,即在空間上隨位置角θ按余弦規律分布,在時間上隨ωt按余弦(正弦)規律脈振,而空間分布的軸線固定不動。如前所述,這種從空間上看軸線固定不動,從時間上看其瞬時值不斷地隨電流的交變而在正、負幅值之間脈振的磁勢(磁場)即稱為脈振磁勢(磁場),物理上稱為駐波。脈振的頻率取決于電流的頻率。如圖7所示,為單相繞組在不同瞬間的基波磁勢波。
②基波磁勢的幅值正比于每對極每相的有效串聯匝數W?Kdp1/p和相電流IΦ。
5 單相繞組的諧波磁勢
線圈產生的矩形波磁勢中除了基波磁勢外,還有一系列高次諧波。對于整數槽繞組,這些諧波中只含有奇次諧波,而不含有偶次諧波。按照上述基波磁勢的合成推導方法,可推導出單相繞組的υ次諧波分量為:
fΦυ(θ,t)=±(1/υ)?(4/π)?2^??(W?Kdpυ/2p)?IΦ?cos(υθ)?cosωt=±FΦυ?cos(υθ)?cosωt (13)
其中:
FΦυ=(1/υ)?(4/π)?2^??(W?Kdpυ/2p)?IΦ
=(1/υ)?0.9?(W?Kdpυ/p)?IΦ
=(1/υ)?(Kdpυ/Kdp1)?FΦ1(14)
以上兩式中Kdpυ為υ次諧波繞組系數。
以上兩式可見,單相繞組產生的諧波磁勢仍然是一個脈振磁勢,從空間上看按υ次諧波分布,波長是基波的1/υ,某一條諧波空間分布軸線(即波峰和波谷的位置)也與基波磁勢重合;從時間上看仍按ωt的余弦規律脈振,脈振頻率與基波相同,諧波磁勢的幅值與諧波次數成反比,與諧波繞組系數成正比,諧波次數越高,諧波幅值越小。另外可以通過減小諧波繞組系數的方法來削弱諧波磁勢。
本期介紹了單相繞組產生的磁勢,推導過程比較復雜,如實在沒有耐心,可以跳過推導部分,但需要記住文中的一些重要結論。簡單歸納一下就是:單相繞組通以正弦交流電流時產生的磁勢是一個脈振磁勢,脈振頻率與電流頻率相同,在空間分布上包括基波和一系列高次(奇次)諧波,基波和高次諧波的峰(谷)值位置與繞組的軸線重合。必須強調一點,上述結論只適用于整數槽繞組,分數槽繞組某些結論不適用,關于分數槽繞組的磁勢還會在以后的文章中詳述。
審核編輯:湯梓紅
-
線圈
+關注
關注
14文章
1813瀏覽量
44346 -
電流
+關注
關注
40文章
6751瀏覽量
131860 -
電機繞組
+關注
關注
0文章
68瀏覽量
10578
原文標題:電機繞組(十二)
文章出處:【微信號:西莫電機論壇,微信公眾號:西莫電機論壇】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
淺談三相繞組磁勢及其合成磁勢基波
反激變壓器副邊繞組電流峰值計算根據能量守恒還是磁動勢守恒
多繞組反激變換器副邊電流峰值計算按照能量守恒還是磁勢守恒
電機基礎知識入門之交流繞組、電勢、磁勢等詳細資料免費下載




 電機繞組的磁勢講解
電機繞組的磁勢講解
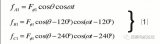
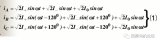










評論