為滿足自動駕駛行車&泊車過程的縱向控制功能需求，需開發(fā)行車功能的縱向控制VLC以及泊車功能的軌跡速度規(guī)劃TSP，其中，VLC負(fù)責(zé)將車輛縱向控制的加速度接口ax轉(zhuǎn)化為驅(qū)動/制動力Fx（包括前饋控制與反饋控制），TSP進(jìn)行S-V關(guān)系式擬合。

VLC控制算法簡介

VLC技術(shù)方案簡介

對于車輛的縱向控制，首先基于ACC模型并選擇合適的控制算法，如極點(diǎn)配置、LQR、MPC等算法（可參考公眾號相關(guān)文章），進(jìn)而通過解算得到系統(tǒng)的控制輸入量即期望加速度。忽略擾動項(xiàng)（前車加速度），得到ACC模型如下：

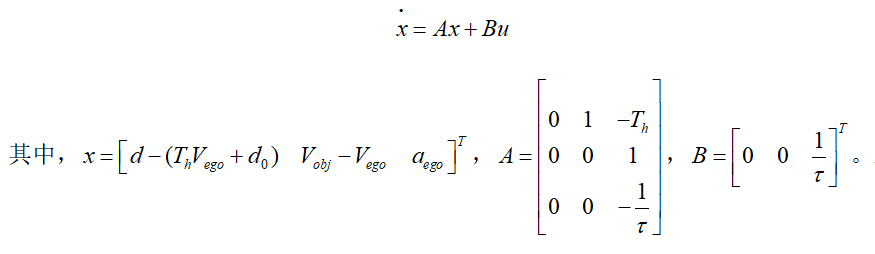
上述式子中：d為兩車間的實(shí)際距離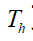，為車頭時距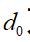，為兩車間靜止時的期望距離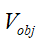，為前車速度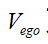，為本車速度，τ為一階慣性環(huán)節(jié)的慣性時間常數(shù)。

控制算法在本處選用LQR，假設(shè)通過選取合適的Q及R后，解算得到反饋系數(shù)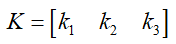：，進(jìn)而得到期望加速度：

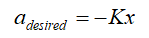
其中，K及x如上述算法所示。算法模型示意圖如下圖1所示：

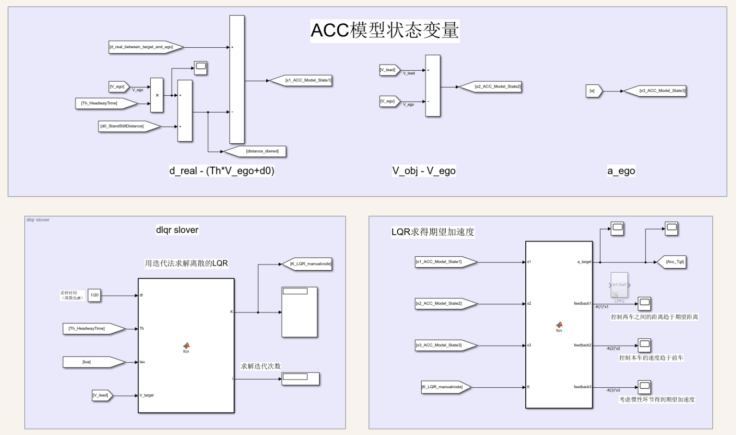
圖1ACC模型及LQR算法示意圖

在得到期望加速度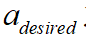之后，根據(jù)車輛的縱向行駛方程進(jìn)一步計(jì)算得到期望的驅(qū)動扭矩或者制動壓力。車輛的縱向行駛方程如下所示：

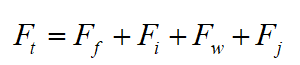
即：

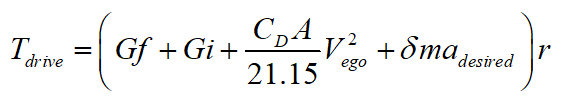
其中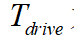，為期望的驅(qū)動力矩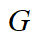，為本車的重力，i為道路坡度（縱坡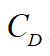），為空氣阻力系數(shù)，A為迎風(fēng)面積，δ為旋轉(zhuǎn)質(zhì)量換算系數(shù)，m為本車質(zhì)量。

上述通過車輛縱向行駛方程所求得的期望驅(qū)動力矩為前饋值，由于模型存在建模的誤差及不確定性，因此在此引入反饋對其進(jìn)行補(bǔ)償，本處所采用的反饋控制器為PID控制器，該控制器的輸入為期望加速度與實(shí)際加速度的偏差，控制器的控制輸出為驅(qū)動扭矩，該值則為反饋值。通過前饋與反饋的結(jié)合，使得該算法具備了更為優(yōu)異的加速度跟蹤性能。算法的示意圖如下圖2所示：

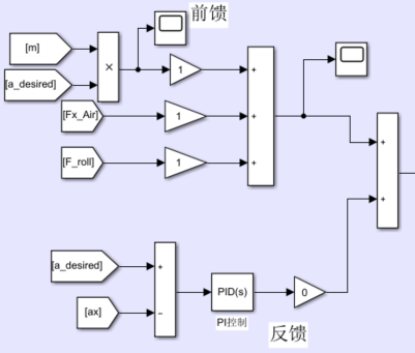
圖2 前饋及反饋算法示意圖

算法的仿真結(jié)果圖（跟車場景：前車在過程中有啟停）如下圖所示：

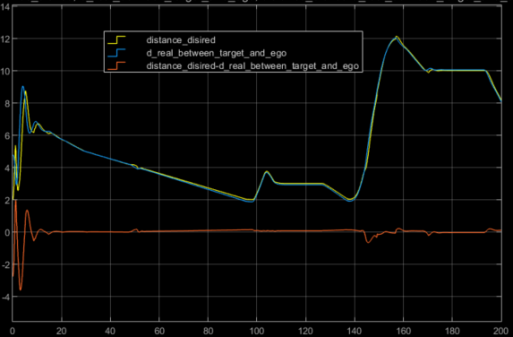
圖3 兩車間期望距離及實(shí)際距離對比結(jié)果圖

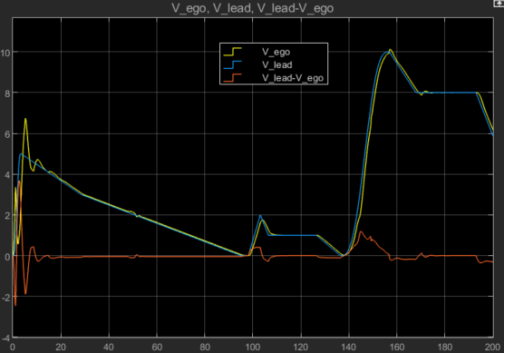
圖4 本車速度及前車速度對比結(jié)果圖

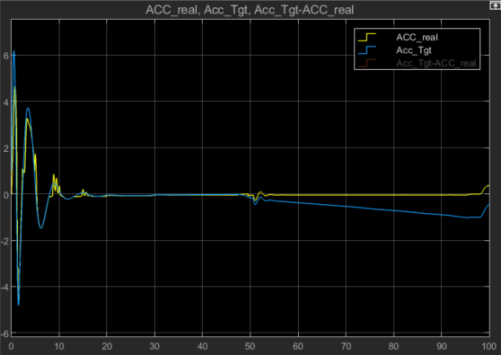
圖5 ACC模型得到的期望加速度與本車實(shí)際加速度對比結(jié)果圖

由圖3、4及圖5可以得到上述算法在跟馳前車上表現(xiàn)較好，對加速度的跟蹤效果尚可。

上述參數(shù)中道路坡度、本車質(zhì)量及狀態(tài)變量中的本車速度需要通過參數(shù)估計(jì)及狀態(tài)估計(jì)得到，而其他一些參數(shù)則可以通過傳感器或者實(shí)驗(yàn)測量得到，在下面部分將詳細(xì)介紹對于待估計(jì)參數(shù)及狀態(tài)變量的參數(shù)估計(jì)算法及狀態(tài)估計(jì)算法。

車速估計(jì)

在縱坡等路段，車輛的加速度傳感器能夠測得車輛的縱向加速度，但由于坡度的存在，其測量值往往可能存在較大偏差，需要通過濾波算法，對加速度進(jìn)行重新估計(jì)，求得車輛速度、加速度的準(zhǔn)確估計(jì)后，可根據(jù)加速度的測量值和估計(jì)值估計(jì)得到路面的坡度。

首先，利用輪速傳感器測得的4個車輪轉(zhuǎn)速估算車速：

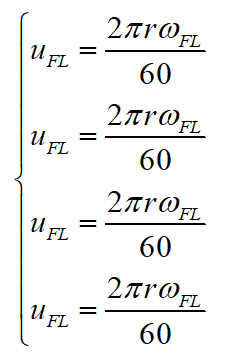
其中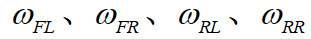，為4個輪的輪速，可由輪速傳感器得到。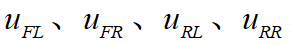為4個車輪旋轉(zhuǎn)的當(dāng)量車速。因?yàn)樵谲囕v運(yùn)動過程中，輪胎不可避免地存在驅(qū)動打滑、制動打滑等狀態(tài)，所以需要對車輪打滑時地速度進(jìn)行修正，此時使用上一時刻的速度與加速度估算當(dāng)量車速。

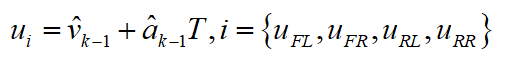
其中，T為采樣周期，i為發(fā)生打滑的車輪。下一步將4個車輪旋轉(zhuǎn)的當(dāng)量車速按照從小到大進(jìn)行升序排列：

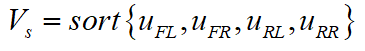
當(dāng)汽車加速度為正值時，驅(qū)動輪可能發(fā)生打滑，從動輪的當(dāng)量車速更加接近真實(shí)車速，選擇第三大的當(dāng)量車速作為參考車速；反之，選擇第二大當(dāng)量車速作為參考車速；否則將4個當(dāng)量車速的平均值作為參考車速：

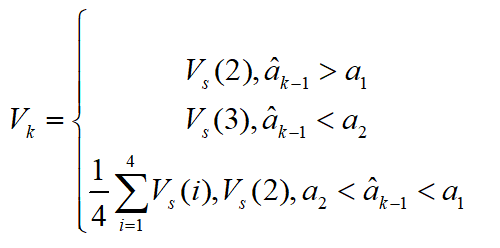
其中，是判斷車輛驅(qū)動或者制動工況的加速度閾值，將由上式獲得的參考車速作為車速的測量值。 在得到車速的測量值之后，再結(jié)合卡爾曼濾波對其進(jìn)一步的處理，得到濾波后的車速值。具體過程如下：

（1）建立系統(tǒng)狀態(tài)方程：

假設(shè)車輛在一個周期內(nèi)勻加速行駛（CA模型），狀態(tài)變量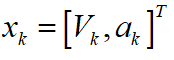，其中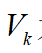為當(dāng)前車輛行駛的速度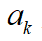，為當(dāng)前車輛行駛的加速度。可得到系統(tǒng)的狀態(tài)方程：

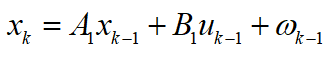
其中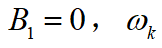，為高斯白噪聲。當(dāng)采樣周期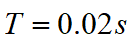時，狀態(tài)轉(zhuǎn)移矩陣為：

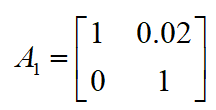
（2）建立測量方程：

車輛在當(dāng)前周期內(nèi)的行駛速度將使用上述的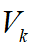，加速度則通過加速度傳感器（IMU）獲得，則測量方程為：

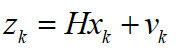
其中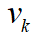，為測量噪聲。由于系統(tǒng)狀態(tài)完全可測，故觀測矩陣為H為單位矩陣。 （3）卡爾曼濾波： 給定濾波過程的初始狀態(tài)，再根據(jù)如下所示的卡爾曼濾波的5個公式即可對車速進(jìn)行濾波，最終得到車速的估計(jì)值及加速度的估計(jì)值。

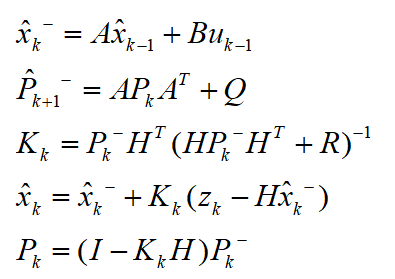
其中，測量信息為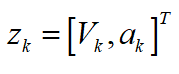：。 坡度估計(jì) 設(shè)上述通過卡爾曼濾波估計(jì)得到的加速度為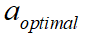，則可以根據(jù)下式估算道路坡度i：

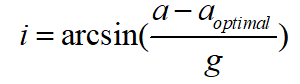
其中，a為IMU測得的車輛縱向加速度，g為重力加速度，該方法的原理示意圖如下所示：

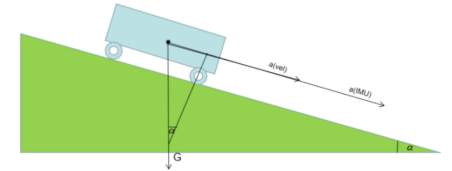
圖6 縱向加速度測量

質(zhì)量估計(jì)

對車輛縱向行駛方程進(jìn)行變形得：

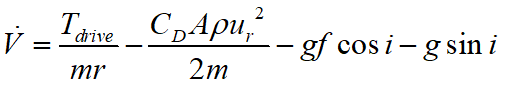
考慮到公路的設(shè)計(jì)規(guī)范，道路坡度一般較小，因此對上式進(jìn)行簡化，得：

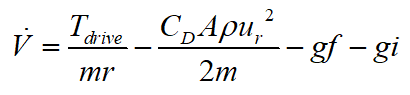
假設(shè)質(zhì)量變化及坡度變化為一個慢時變過程，可得：

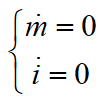
選取V、m、i為狀態(tài)變量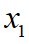，構(gòu)建狀態(tài)空間表達(dá)：

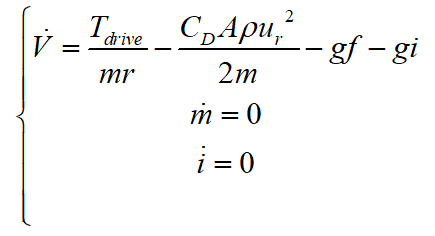
對其進(jìn)行離散化得：

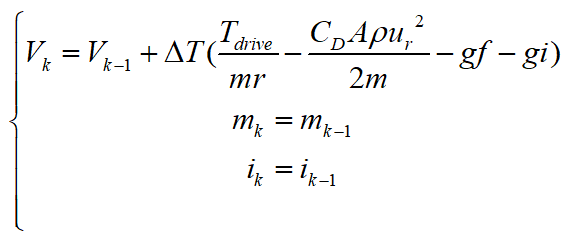
選取車速作為觀測量，則系統(tǒng)的測量方程為：

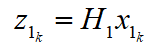
由上述可得系統(tǒng)的狀態(tài)空間表達(dá)：

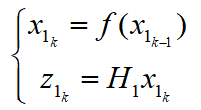
對上述系統(tǒng)使用擴(kuò)展卡爾曼濾波即可重構(gòu)得到系統(tǒng)狀態(tài)，即獲得了質(zhì)量的估計(jì)值。

TSP技術(shù)方案

TSP縱向速度規(guī)劃方案

在自動泊車場景下，本車周圍通常存在許多的障礙物，如：墻壁、立柱、旁邊車位停放的車輛等。如何在不發(fā)生碰撞的情況下，將車輛自動泊入所選定的車位，是自動泊車中的主要技術(shù)點(diǎn)，即路徑規(guī)劃。而在完成了路徑規(guī)劃之后，也需要對其進(jìn)行相應(yīng)的速度規(guī)劃，使得車輛能夠安全、高效、舒適的完成自動泊車任務(wù)。

從人類駕駛員的經(jīng)驗(yàn)出發(fā)，一般距離障礙物越近時，人類駕駛員往往會選擇降低車速，緩行通過，因此，本次TSP縱向速度規(guī)劃主要是基于上述經(jīng)驗(yàn)，對泊車過程中的本車速度進(jìn)行規(guī)劃。

由上所述，本次TSP縱向速度規(guī)劃目標(biāo)是得到本車速度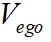與本車與障礙物之間的距離d的關(guān)系。在經(jīng)過分析后，本次規(guī)劃選取三次多項(xiàng)式曲線來進(jìn)行速度規(guī)劃，即速度與加速度的多項(xiàng)式映射關(guān)系為：

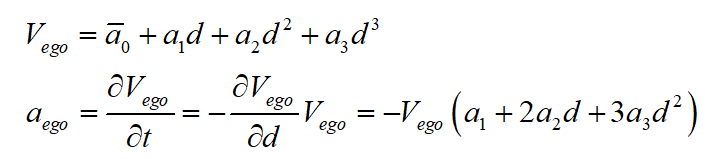
首先確定邊界條件。在規(guī)劃的初始點(diǎn)，本車與障礙物之間的初始距離為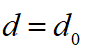，而本車當(dāng)前速度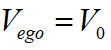，當(dāng)前加速度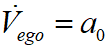；在規(guī)劃的結(jié)束點(diǎn)，車輛成功泊入車位，本車與障礙物的最終距離為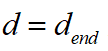，本車規(guī)劃的速度為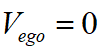。將上述兩個邊界條件帶入三次多項(xiàng)式中，可得：

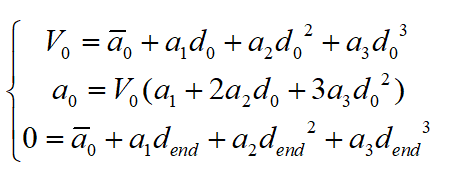
考慮到上述三個邊界條件帶入三次多項(xiàng)式曲線后得到的方程組求解的復(fù)雜度，在此處通過引入中間變量的方式對其進(jìn)行變形，以簡化求解，提高算法的實(shí)時性。通過分析，選取本車從泊車開始累計(jì)的行駛距離S作為中間變量，該中間變量與d之間的關(guān)系如下式：

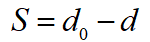
將上式帶入三次多項(xiàng)式曲線中，可得到以S作為自變量的新的三次多項(xiàng)式曲線，表達(dá)式如下：

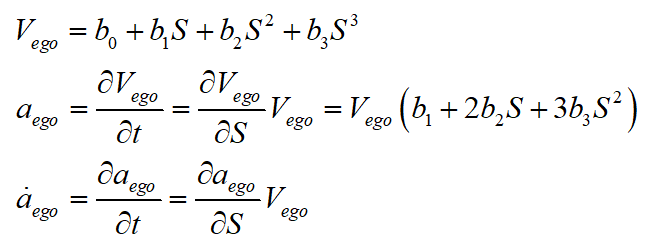
此時，再將三個邊界條件帶入新的三次多項(xiàng)式曲線中可得：

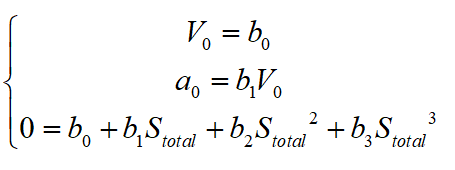
其中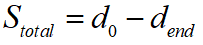，為泊車過程中本車所行駛過的總距離。對上式進(jìn)行解方程組可得：

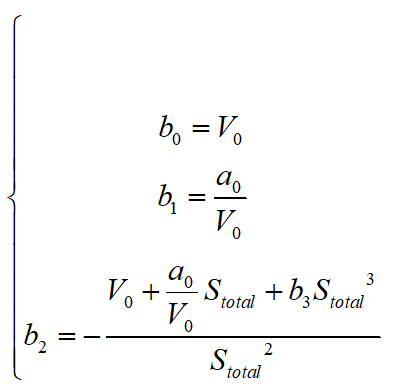
將上式方程組的解代回到速度曲線的三次多項(xiàng)式，可得：

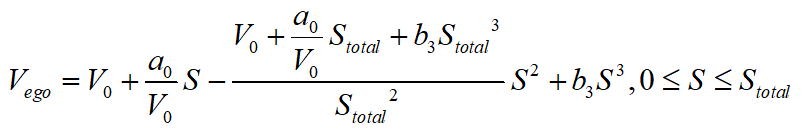
因此，由三個邊界條件所得到的三個約束條件，使得三次多項(xiàng)式曲線的自由變量（系數(shù)）只剩下一個，最后將結(jié)合優(yōu)化的方法來求得該系數(shù)的最優(yōu)值，在此處該自由變量為。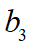

對上式兩邊同時對時間求一階及二階導(dǎo)數(shù)，可得速度和加速度分別為：

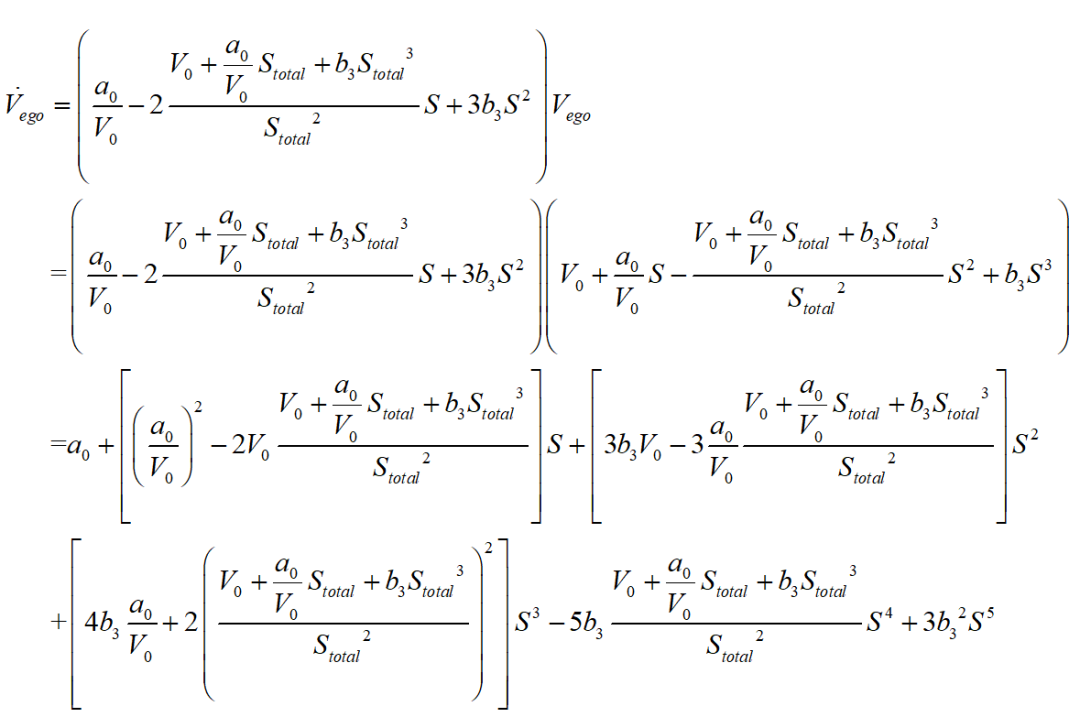
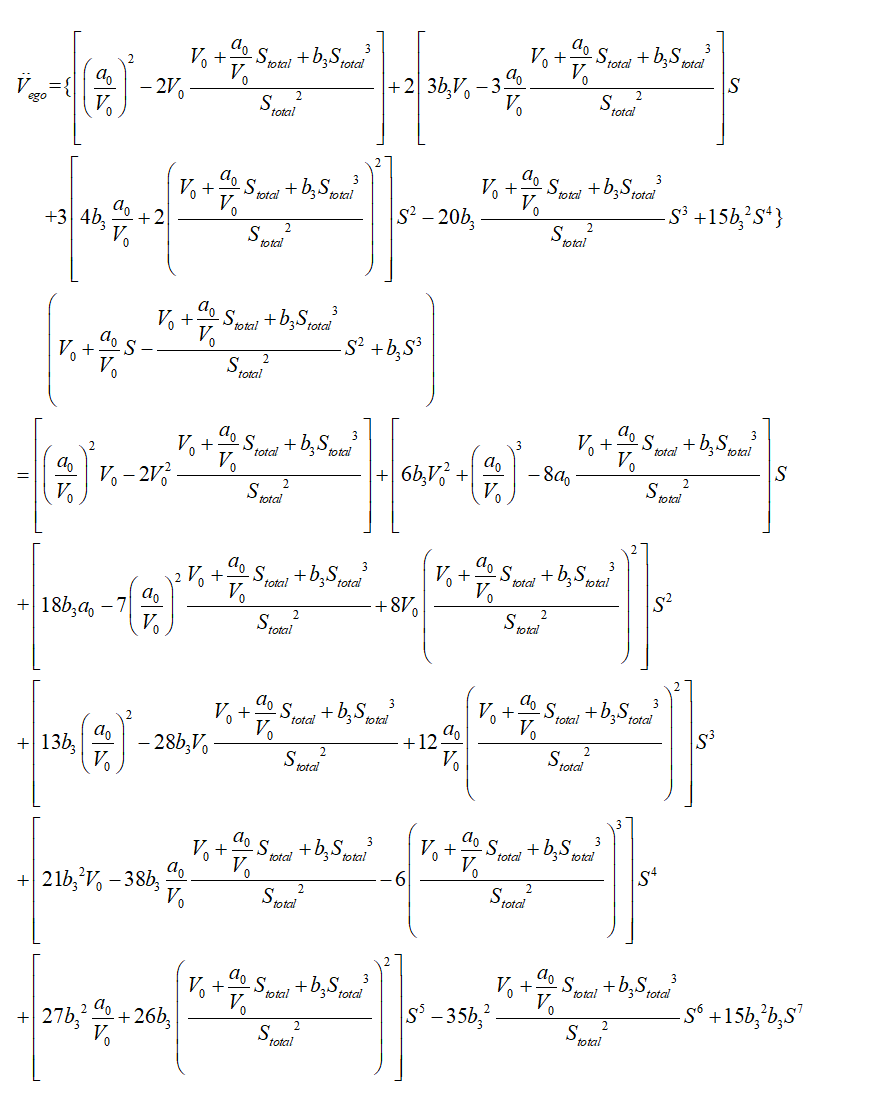
縱向速度優(yōu)化模型

從舒適性的角度出發(fā)，加速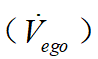度與沖擊度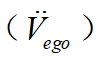應(yīng)當(dāng)盡量的小；從效率的角度出發(fā)，希望車輛完成泊車任務(wù)的時間盡可能的短；因此，在考慮上述目標(biāo)后，設(shè)定目標(biāo)函數(shù)如下：

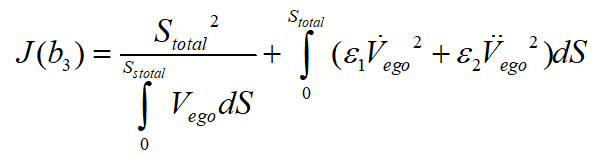
其中，目標(biāo)函數(shù)中的第一項(xiàng)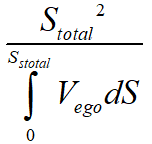的物理意義為完成泊車過程所用的時間，即對應(yīng)效率的目標(biāo)，第二項(xiàng)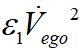及第三項(xiàng)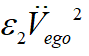則對應(yīng)舒適性的目標(biāo)即平穩(wěn)泊車的目標(biāo)。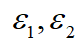為優(yōu)化的權(quán)重系數(shù)。最后將上面的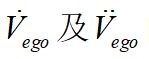的表達(dá)式帶入該代價函數(shù)，化簡可得關(guān)于變量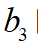的代價函數(shù)如下式：

上述代價函數(shù)為關(guān)于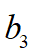的一元多次函數(shù)，目標(biāo)是找到最優(yōu)的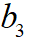讓代價函數(shù)取得最小值。對于一元函數(shù)求極值的問題，使用KKT原理是比較有效的方法，因此，對上式關(guān)于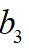進(jìn)行求導(dǎo)，并令該式等于0得到若干個解，最后比較這幾個點(diǎn)的函數(shù)值即可確定最優(yōu)的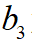解，而根據(jù)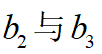的關(guān)系也得到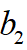，至此所規(guī)劃的速度曲線已經(jīng)被唯一確定，完成了TSP縱向速度規(guī)劃。

泊車速度規(guī)劃求解

TSP車速規(guī)劃相關(guān)的算法如下圖示：

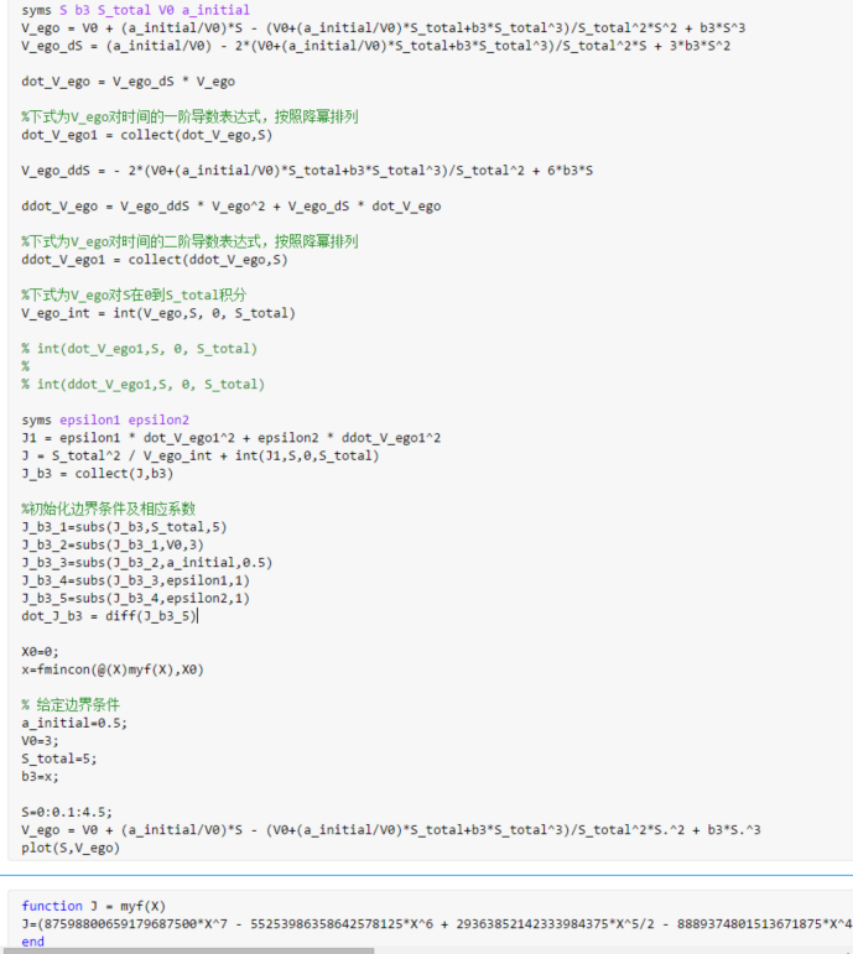
在本次的算法測試中初始條件設(shè)置為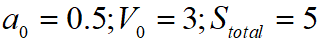：，最后求得的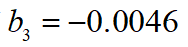，完成整個泊車過程的時間為2.286s，帶入得到：

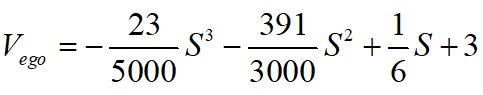
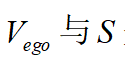，的關(guān)系圖如下圖所示：

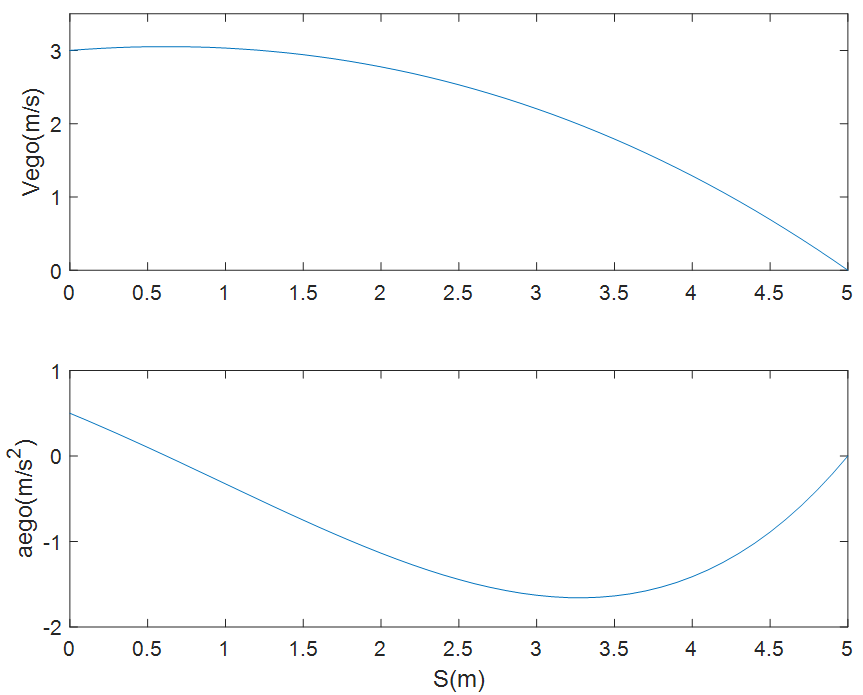
圖7 規(guī)劃的速度與加速度

上述算法還是較復(fù)雜，考慮到其實(shí)時求解問題，可將其簡化，假設(shè)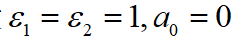，則簡化后關(guān)于變量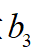的代價函數(shù)如下式：

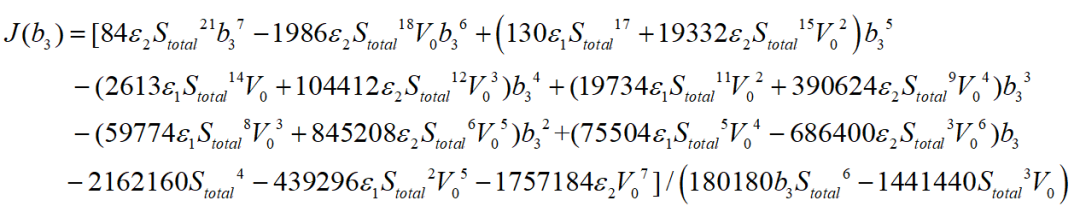
其極值點(diǎn)為：

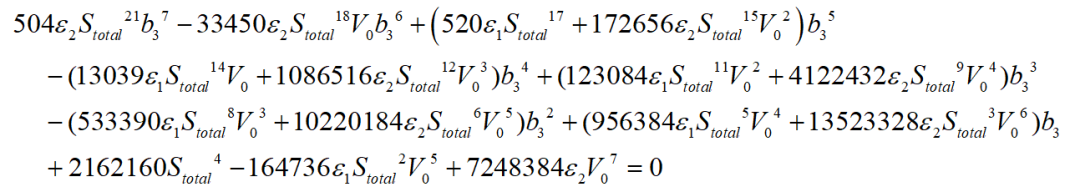
考慮到上述極值點(diǎn)條件有多個可行解，快速尋找其最優(yōu)解也是一個較為復(fù)雜的問題，可利用泊車完成一半時候的規(guī)劃速度非負(fù)這個條件來加以判斷，因此設(shè)定驗(yàn)證條件如下所示：

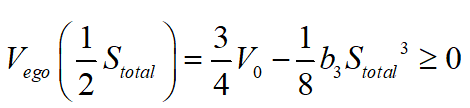
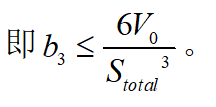
在同樣邊界條件下可求得有兩個可行解，分別如下圖所示。

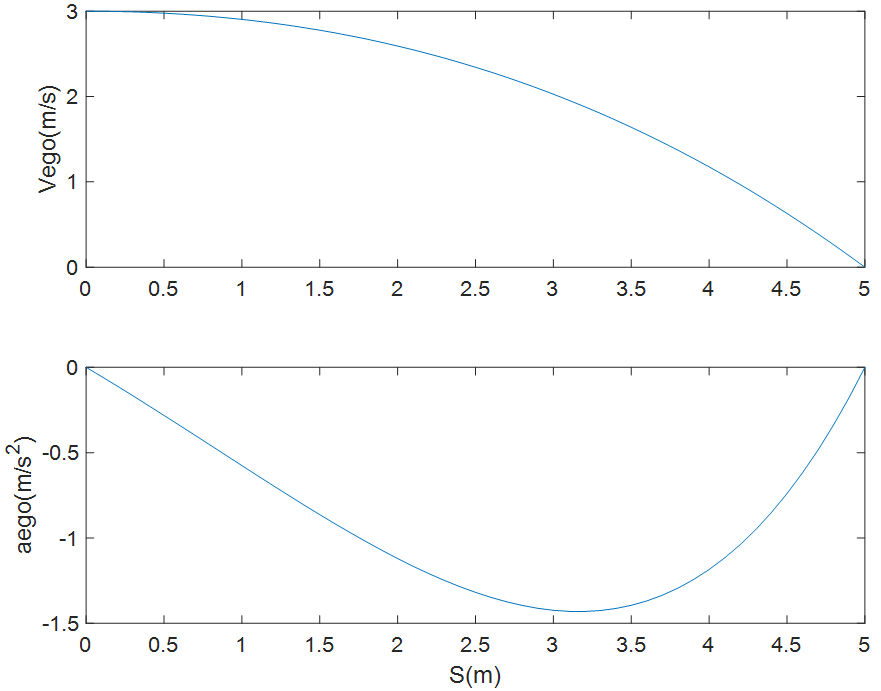
圖8 規(guī)劃的速度與加速度（可行解1）

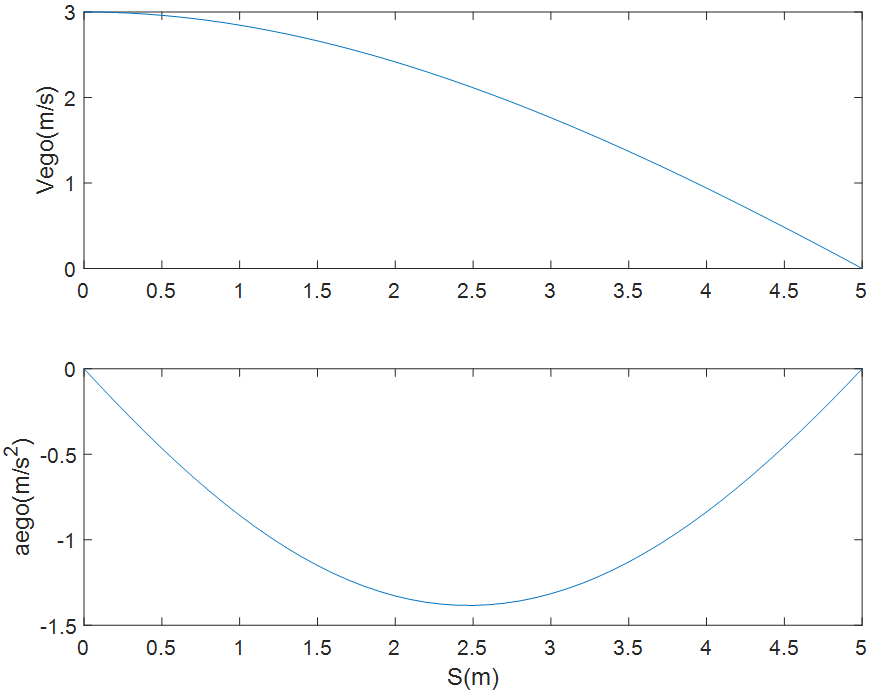
圖9 規(guī)劃的速度與加速度（可行解2）

?審核編輯：湯梓紅