評論:二階過濾器
當我說“二階”濾波器時,我指的是使用電感 - 電容(LC)諧振或放大器的濾波器,以產生真正的二階傳遞函數。您可以通過級聯兩個一階無源濾波器來實現兩極頻率響應,但是得到的電路沒有復共軛極點,因此傳輸函數無法優化,因為Q因子始終為0.5。相比之下,設計人員可以控制基于諧振或放大器的二階濾波器的Q因子,使其有利于平坦通帶,線性相位響應或快速通帶到阻帶轉換。
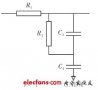
本文中的信息一般適用于二階濾波器,但在我撰寫本文時,我想到的電路是下面顯示的RLC二階低通濾波器。
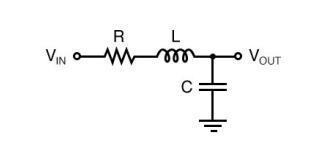
該濾波器的截止頻率由電容器和電感器的值決定,Q因子可以通過改變電阻器的值來改變。當你與Nyquist圖的工作,需要記住的是截止頻率(很重要的ω 二階濾波器)是不是一定-3dB頻率。在增益ω 可以是-3分貝,比-3 dB的降低,或小于-3分貝根據過濾器的Q因子大。
奈奎斯特圖中的象限
您可能會注意到關于二階奈奎斯特圖的第一件事是它延伸到復平面的左下象限。例如:
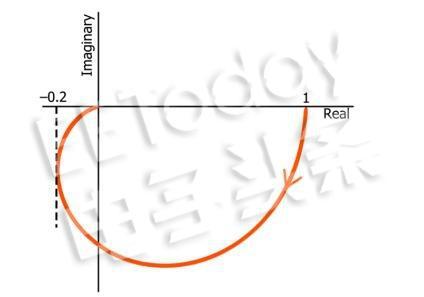
請注意,本文中顯示的所有圖都不包含負頻率。
由于曲線延伸到左下象限但不進入左上象限,我們立即知道它代表二階濾波器。為什么?那么,負虛軸對應于-90°的相移,如果奈奎斯特跡線穿過該軸并延伸到左下象限,則濾波器必須具有多個極點,因為您只能獲得-90°的相位每極移位。它不能有三個極點,因為角度不會超過-180°(對應于負實軸)。你可以看到曲線在接近原點時傾向于-180°,正如隨著頻率向無窮大增加,兩極濾波器的相移漸近接近-180°。
二階濾波器的截止頻率
與一階奈奎斯特圖一樣,二階濾波器的奈奎斯特圖不會給出截止頻率。然而,與一階情況相比,我們無法通過在曲線上尋找幅度響應為1/√2的點來找到一般的截止頻率位置。這是因為(如上所述)在增益ω 由電路的Q因子的影響。然而,無論Q如何,相移在截止頻率下始終為-90°。因此,對于二階低通濾波器,截止頻率對應于奈奎斯特曲線與負虛軸相交的點。
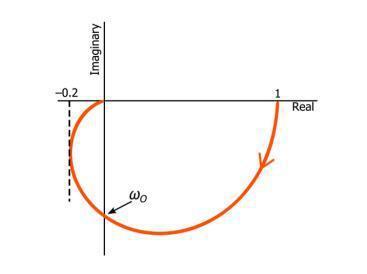
二階奈奎斯特圖中的Q因子
即使是如上所示的基本奈奎斯特圖也可以提供關于二階濾波器Q因子的重要定性信息。如果正在處理無源低通濾波器,那么可以假設低頻增益將是統一的。因此,奈奎斯特曲線將以幅度響應1開始,并且由于在非常低的頻率下相移基本上為零,因此奈奎斯特跡線源自正實軸上的值1。
當頻率增加時,曲線離開實軸后的操作會給我們提供關于幅度響應的信息,而這反過來又會給我們關于Q的信息。首先,如果距離原點的距離增加超過初始值,當輸入頻率接近截止頻率時,濾波器的增益會增加,因此Q必須足夠高才能產生一些峰值。
此外,通過比較截止頻率下的增益和初始增益,可以形成截止頻率區域中幅度響應的一般概念。如果截止頻率增益明顯高于低頻增益,則您知道濾波器具有相對較高的Q值。下圖顯示了具有相同截止頻率但不同Q的RLC濾波器的兩條奈奎斯特曲線。橙色曲線表示一個臨界阻尼濾波器,即Q=0.5,ωo處的增益為-6 dB。藍色曲線表示欠阻尼濾波器;其Q系數約為1.7,ωo處的增益為+4.7 dB。
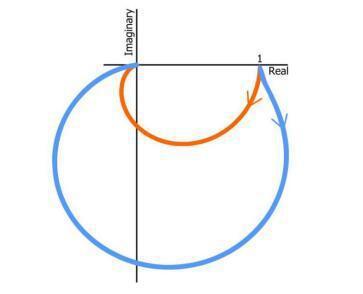
總結
我們已經看到,用于低通濾波器的奈奎斯特圖給出了關于傳遞函數中極點數的清晰、直接的信息,并且我們探討了奈奎斯特曲線的一般形狀與二階濾波器的Q因子之間的關系。
-
電容器
+關注
關注
64文章
6208瀏覽量
99336 -
電感器
+關注
關注
20文章
2325瀏覽量
70420 -
諧振放大器
+關注
關注
1文章
15瀏覽量
12689 -
二階濾波器
+關注
關注
0文章
7瀏覽量
8185 -
RLC電路
+關注
關注
2文章
26瀏覽量
7156
發布評論請先 登錄
相關推薦
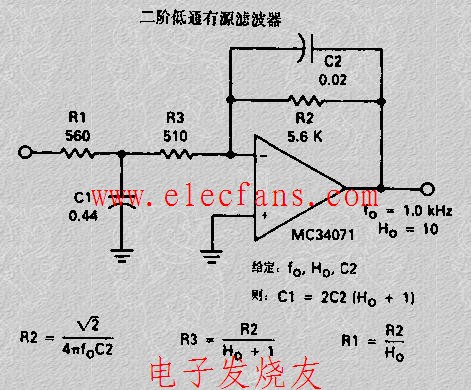
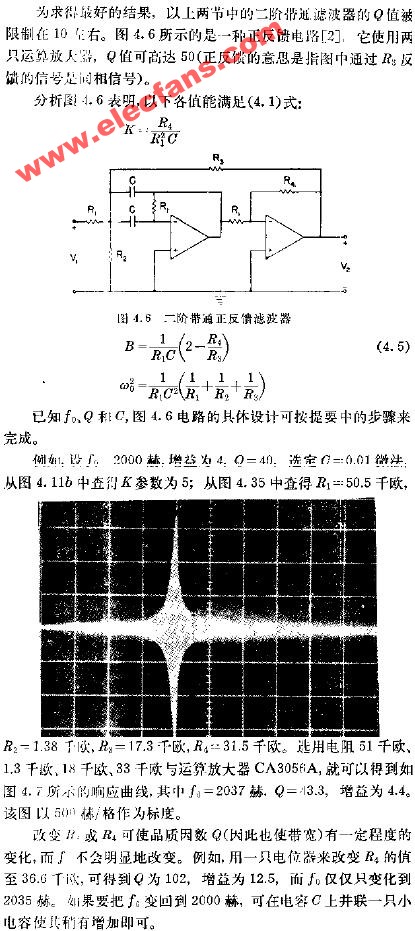
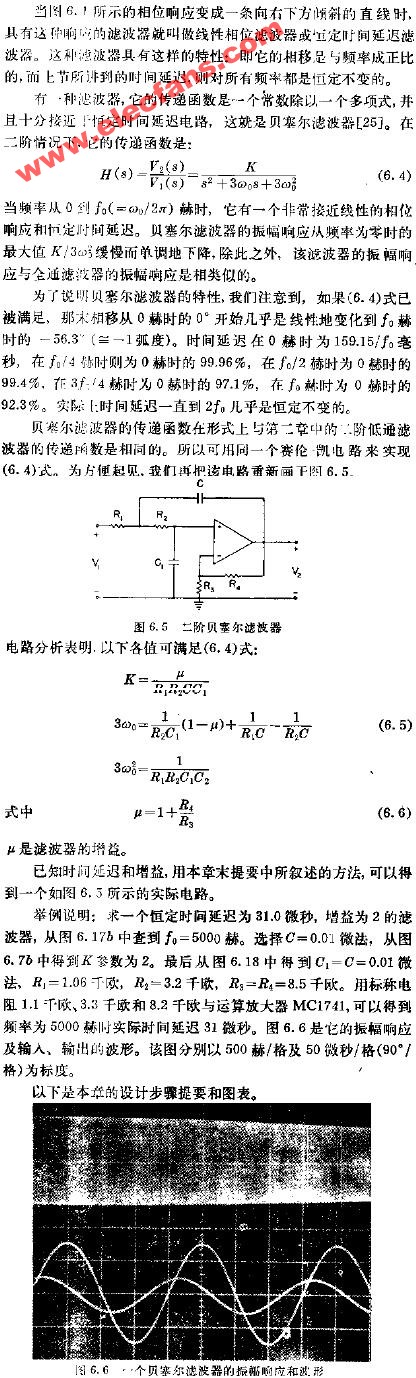
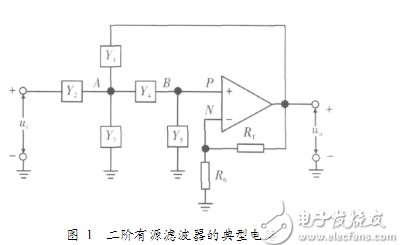
二階有源濾波器設計





 二階濾波器的奈奎斯特圖簡析
二階濾波器的奈奎斯特圖簡析











評論