作者：王立奇英特爾邊緣計算創新大使

一、PINN—加入物理約束的神經網絡

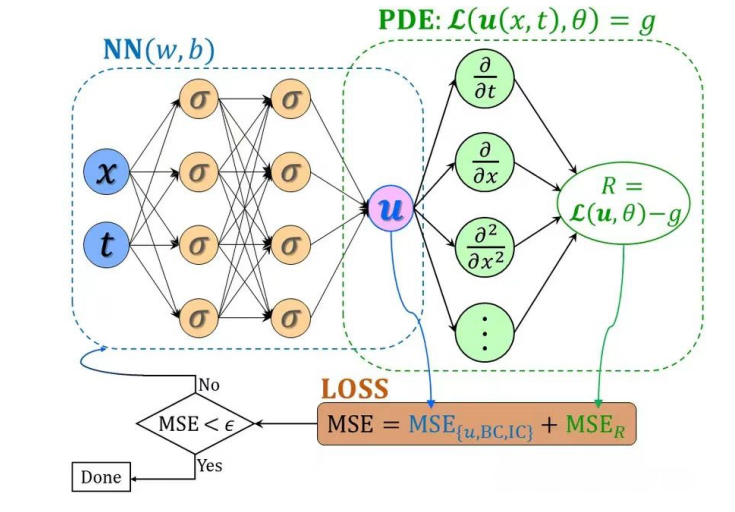
基于物理信息的神經網絡（Physics-informed Neural Network，簡稱PINN），是一類用于解決有監督學習任務的神經網絡，它不僅能夠像傳統神經網絡一樣學習到訓練數據樣本的分布規律，而且能夠學習到數學方程描述的物理定律。與純數據驅動的神經網絡學習相比，PINN在訓練過程中施加了物理信息約束，因而能用更少的數據樣本學習到更具泛化能力的模型。本文主要解析這種神經網絡以及相關應用。

2019年，來自布朗大學應用數學的研究團隊提出了一種用物理方程作為運算限制的“物理激發的神經網絡”(PINN)并發表在了計算物理學領域權威雜志《計算物理學期刊》(Journal of Computational Physics)上。這篇論文一經發表就獲得了大量關注。這篇論文因為代碼體系的完整性使得開發人員們很容易上手把相關的學習框架應用到不同領域上去。所以在發表不久之后，一系列不同的PINN也被其他研究者開發出來。甚至可以不夸張的說，PINN是目前AI物理領域論文中最常見到的框架和詞匯之一。

算法描述

而所謂的物理神經網絡，其實就是把物理方程作為限制加入神經網絡中使訓練的結果滿足物理規律。而這個所謂的限制是怎么實現的？其實就是通過把物理方程的迭代前后的差值加到神經網絡的損失函數里面去，讓物理方程也“參與”到了訓練過程。這樣，神經網絡在訓練迭代時候優化的不僅僅是網絡自己的損失函數，還有物理方程每次迭代的差，使得最后訓練出來的結果就滿足物理規律了。

二、DeepXDE

DeepXDE 由 Lu Lu 在布朗大學 George Karniadakis 教授的指導下于 2018 年夏季至 2020年夏季開發，并得到 PhILM 的支持。DeepXDE 最初是在布朗大學的 Subversion 中自行托管的，名稱為 SciCoNet（科學計算神經網絡）。2019 年 2 月 7 日，SciCoNet 從 Subversion 遷移到 GitHub，更名為 DeepXDE。

DeepXDE特性

DeepXDE 已經實現了如上所示的許多算法，并支持許多特性：

復雜的域幾何圖形，沒有專制網格生成。原始幾何形狀是間隔、三角形、矩形、多邊形、圓盤、長方體和球體。其他幾何可以使用三個布爾運算構建為構造實體幾何(CSG)：并集、差集和交集。

多物理場，即（時間相關的）耦合偏微分方程。

5 種類型的邊界條件(BC)：Dirichlet、Neumann、Robin、周期性和一般 BC，可以在任意域或點集上定義。

不同的神經網絡，例如（堆疊/非堆疊）全連接神經網絡、殘差神經網絡和（時空）多尺度傅里葉特征網絡。

6種抽樣方法：均勻抽樣、偽隨機抽樣、拉丁超立方抽樣、Halton序列、Hammersley序列、Sobol序列。

訓練點可以在訓練期間保持不變，也可以每隔一定的迭代重新采樣一次。

方便保存訓練期間的模型，并加載訓練好的模型。

使用 dropout 的不確定性量化。

許多不同的（加權）損失、優化器、學習率計劃、指標等回調，用于在訓練期間監控模型的內部狀態和統計信息，例如提前停止。

使用戶代碼緊湊，與數學公式非常相似。

DeepXDE 的所有組件都是松耦合的，因此 DeepXDE 結構良好且高度可配置。

可以輕松自定義 DeepXDE 以滿足新的需求。

數值算例

（1）問題設置

我們將求解由下式給出的非線性薛定諤方程：

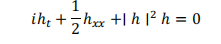
周期性邊界條件為：

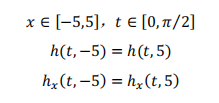
初始條件為：

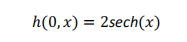
Deepxde 只使用實數，因此我們需要明確拆分復數 PDE 的實部和虛部。

代替單個殘差：

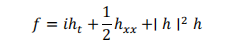
我們得到兩個（實值）殘差：

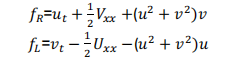
其中 u ( x , t )和 v ( x , t )分別表示h的實部和虛部。

import numpy as np
import deepxde as dde

#用于繪圖

import matplotlib.pyplot as plt
from scipy.interpolate import griddata


x_lower = -5
x_upper = 5
t_lower = 0
t_upper = np.pi / 2

左滑查看更多

#創建2D域（用于繪圖和輸入）

x = np.linspace(x_lower, x_upper, 256)
t = np.linspace(t_lower, t_upper, 201)
X, T = np.meshgrid(x, t)

左滑查看更多

#整個域變平

X_star = np.hstack((X.flatten()[:, None], T.flatten()[:, None]))

左滑查看更多

#空間和時間域/幾何（對于deepxde模型）

space_domain = dde.geometry.Interval(x_lower, x_upper)
time_domain = dde.geometry.TimeDomain(t_lower, t_upper)
geomtime = dde.geometry.GeometryXTime(space_domain, time_domain)

左滑查看更多

#損失的“物理信息”部分

def pde(x, y):
  """
  INPUTS:
    x: x[:,0] 是 x 坐標
      x[:,1] 是 t 坐標
    y: 網絡輸出，在這種情況下:
      y[:,0] 是 u(x,t) 實部
      y[:,1] 是 v(x,t) 虛部
  OUTPUT:
    標準形式的 pde，即必須為零的東西
  """


  u = y[:, 0:1]
  v = y[:, 1:2]

左滑查看更多

#在'jacobian'中，i是輸出分量，j是輸入分量

 u_t = dde.grad.jacobian(y, x, i=0, j=1)
  v_t = dde.grad.jacobian(y, x, i=1, j=1)


  u_x = dde.grad.jacobian(y, x, i=0, j=0)
  v_x = dde.grad.jacobian(y, x, i=1, j=0)

左滑查看更多

#在“hessian”中，i 和 j 都是輸入分量。（Hessian 原則上可以是 d^2y/dxdt、d^2y/d^2x 等）

#輸出組件由“組件”選擇

 u_xx = dde.grad.hessian(y, x, component=0, i=0, j=0)
  v_xx = dde.grad.hessian(y, x, component=1, i=0, j=0)


  f_u = u_t + 0.5 * v_xx + (u ** 2 + v ** 2) * v
  f_v = v_t - 0.5 * u_xx - (u ** 2 + v ** 2) * u


  return [f_u, f_v]

左滑查看更多

#邊界條件和初始條件

#周期性邊界條件

bc_u_0 = dde.PeriodicBC(
  geomtime, 0, lambda _, on_boundary: on_boundary, derivative_order=0, component=0
)
bc_u_1 = dde.PeriodicBC(
  geomtime, 0, lambda _, on_boundary: on_boundary, derivative_order=1, component=0
)
bc_v_0 = dde.PeriodicBC(
  geomtime, 0, lambda _, on_boundary: on_boundary, derivative_order=0, component=1
)
bc_v_1 = dde.PeriodicBC(
  geomtime, 0, lambda _, on_boundary: on_boundary, derivative_order=1, component=1
)

左滑查看更多

#初始條件

def init_cond_u(x):
  "2 sech(x)"
  return 2 / np.cosh(x[:, 0:1])
  
def init_cond_v(x):
  return 0




ic_u = dde.IC(geomtime, init_cond_u, lambda _, on_initial: on_initial, component=0)
ic_v = dde.IC(geomtime, init_cond_v, lambda _, on_initial: on_initial, component=1)
data = dde.data.TimePDE(
  geomtime,
  pde,
  [bc_u_0, bc_u_1, bc_v_0, bc_v_1, ic_u, ic_v],
  num_domain=10000,
  num_boundary=20,
  num_initial=200,
  train_distribution="pseudo",
)

左滑查看更多

#網絡架構

net = dde.maps.FNN([2] + [100] * 4 + [2], "tanh", "Glorot normal")


model = dde.Model(data, net)

左滑查看更多

Adam優化

#強烈建議使用GPU加速系統.

model.compile("adam", lr=1e-3, loss="MSE")
model.train(epochs=1000, display_every=100)

左滑查看更多

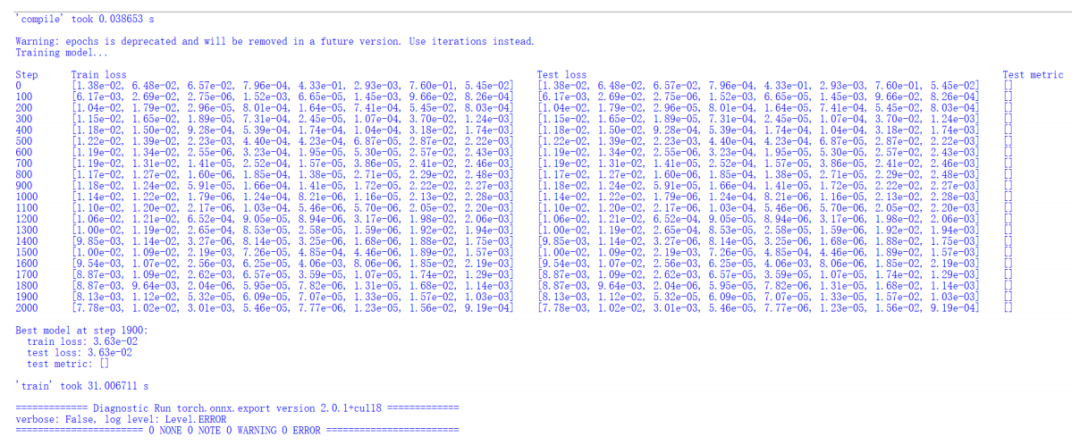
L-BFGS優化

dde.optimizers.config.set_LBFGS_options(
  maxcor=50,
  ftol=1.0 * np.finfo(float).eps,
  gtol=1e-08,
  maxiter=1000,
  maxfun=1000,
  maxls=50,
)
model.compile("L-BFGS")
model.train()
Compiling model...
'compile' took 0.554160 s


Training model...


Step   Train loss                                     Test loss                                      Test metric
1000   [1.25e-02, 1.32e-02, 2.72e-06, 3.28e-04, 5.27e-06, 4.65e-06, 2.24e-02, 1.31e-03]  [1.25e-02, 1.32e-02, 2.72e-06, 3.28e-04, 5.27e-06, 4.65e-06, 2.24e-02, 1.31e-03]  [] 
2000   [7.03e-04, 7.62e-04, 6.76e-06, 1.33e-05, 2.88e-07, 8.49e-06, 4.01e-04, 3.86e-05]                                              
INFOOptimization terminated with:
 Message: STOP: TOTAL NO. of f AND g EVALUATIONS EXCEEDS LIMIT
 Objective function value: 0.001928
 Number of iterations: 945
 Number of functions evaluations: 1001
2001   [7.18e-04, 7.43e-04, 6.27e-06, 1.23e-05, 2.94e-07, 8.89e-06, 4.01e-04, 3.82e-05]  [7.18e-04, 7.43e-04, 6.27e-06, 1.23e-05, 2.94e-07, 8.89e-06, 4.01e-04, 3.82e-05]  [] 


Best model at step 2001:
 train loss: 1.93e-03
 test loss: 1.93e-03
 test metric: []


'train' took 179.449384 s












(,
 )

左滑查看更多

#做預測

prediction = model.predict(X_star, operator=None)


u = griddata(X_star, prediction[:, 0], (X, T), method="cubic")
v = griddata(X_star, prediction[:, 1], (X, T), method="cubic")


h = np.sqrt(u ** 2 + v ** 2)

左滑查看更多

#繪制預測

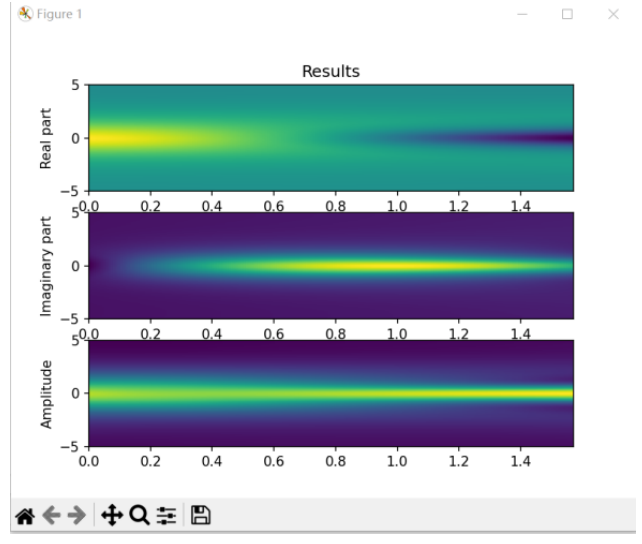
fig, ax = plt.subplots(3)


ax[0].set_title("Results")
ax[0].set_ylabel("Real part")
ax[0].imshow(
  u.T,
  interpolation="nearest",
  cmap="viridis",
  extent=[t_lower, t_upper, x_lower, x_upper],
  origin="lower",
  aspect="auto",
)
ax[1].set_ylabel("Imaginary part")
ax[1].imshow(
  v.T,
  interpolation="nearest",
  cmap="viridis",
  extent=[t_lower, t_upper, x_lower, x_upper],
  origin="lower",
  aspect="auto",
)
ax[2].set_ylabel("Amplitude")
ax[2].imshow(
  h.T,
  interpolation="nearest",
  cmap="viridis",
  extent=[t_lower, t_upper, x_lower, x_upper],
  origin="lower",
  aspect="auto",
)


plt.show()

左滑查看更多

三、生成OpenVINO IR模型

如需使用LabVIEW OpenVINO推理deepxde的模型，需要做以下幾步：

將deepxde模型轉成onnx模型作為中間件：

代碼中，我們首先要創建一個和X_star的形狀相同的X2作為參考輸入（X2必須是cpu上的矩陣），其次是新建一個基于cpu的mode2，其權重和model完全一致。最后使用torch.onnx.export生成onnx模型。

使用命令行將onnx模型轉為IR模型：

mo --input_model Schrodinger.onnx --input_shape "[256,2]"

左滑查看更多

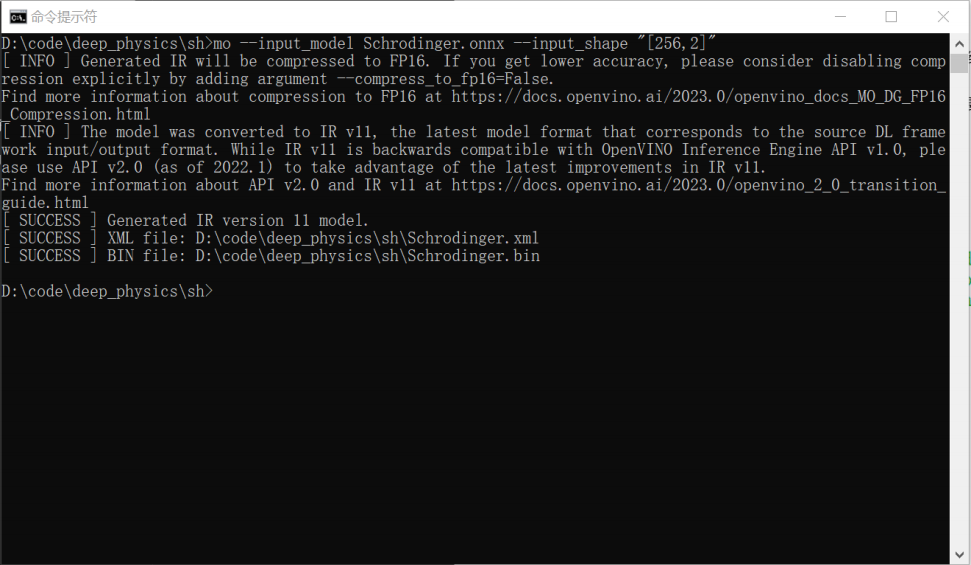
命令中，我們將輸入的形狀設置為256*2，其中第0列為位置x，第1列為時間t。256為我們設置的每個時間點需要推理的x的點數，可以為任意長度。

完成上述兩個步驟后，我們可以看到文件夾里多了三個文件Schrodinger.onnx、Schrodinger.xml和Schrodinger.bin。其中onnx為pytorch生成的onnx模型，xml和bin為mo生成的OpenVINO IR模型。

四、LabVIEW調用IR模型

LabVIEW是NI推出的圖形化編程環境，在科研、工業測控領域有著廣泛的應用。使用LabVIEW的波形圖、強度圖等控件，可以使用戶更直觀的觀測自己模型的訓練結果。

使用我們編寫好的Schrodinger_OpenVINO.vi，即可快速推理Schrodinger方程的OpenVINO模型。以下是使用LabVIEW調用模型的步驟：

1. 初始化模型：使用LoadIR.vi調用xml和bin文件，推理引擎可使用CPU或GPU（Intel核顯或獨顯）；

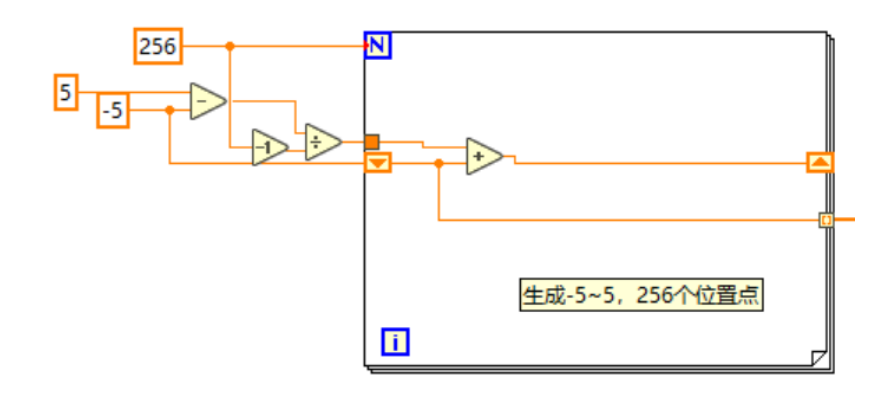
2. 初始化位置。根據我們訓練時用的參數，需要模擬-5~5范圍內任意數量的位置點（本案例中使用256個位置點）。

3. 初始化時間，根據我們訓練的參數，需要模擬0~pi/2范圍內任意數量的時間點（本案例中使用201個時間點。

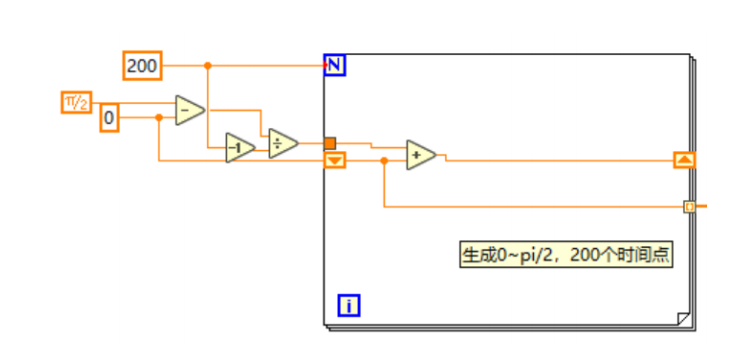
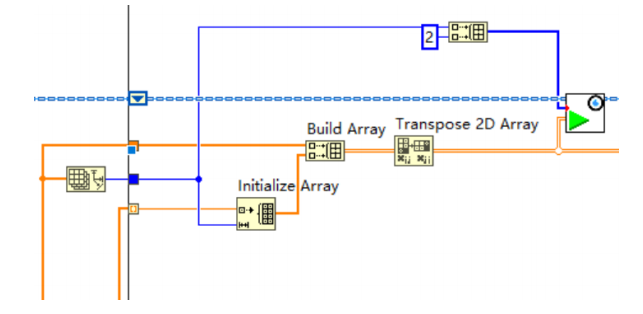
4. 推理模型時。每次循環將某一個時間點復制256份，和所有的256個位置點組成2*256的二維數組，然后轉置成256*2的數組，輸入至網絡中。

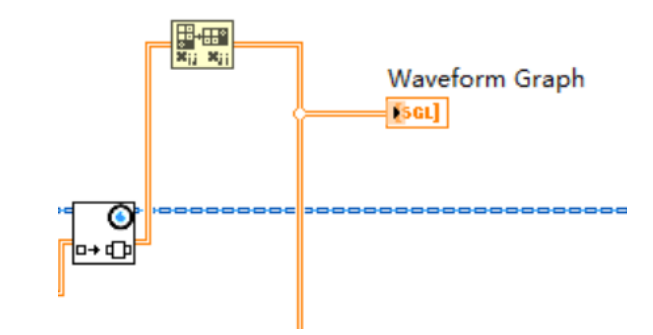
5. 獲取輸出。輸出為256*2，但和輸入的意義不同：其中第0列為波函數h的實部，第1列為h的虛部。因此需要將結果轉置成2*256，后，方能使用波形圖（Waveform Graph）顯示兩條曲線。

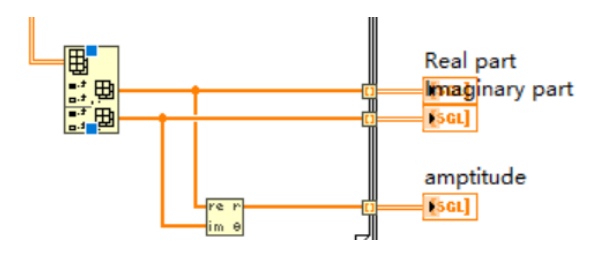
6. 獲取整個時間段、所有位置的結果。使用For循環索引，保存所有時間段實部、虛部和幅值的結果，并顯示在強度圖上。

7. 使用release.vi關閉OpenVINO模型。

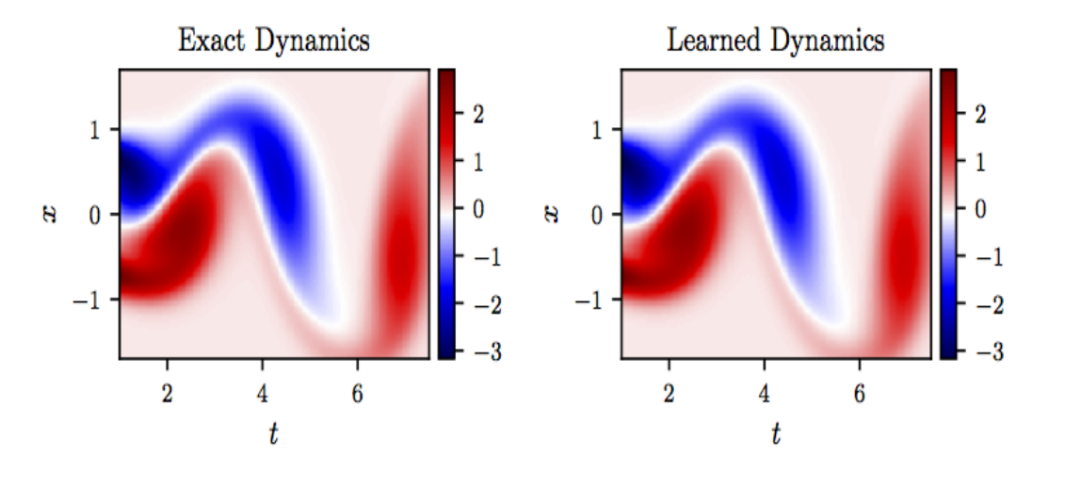
運行程序。我們使用Intel A770獨立顯卡(設備名稱為GPU.1)運行該模型。運行結果如下圖：

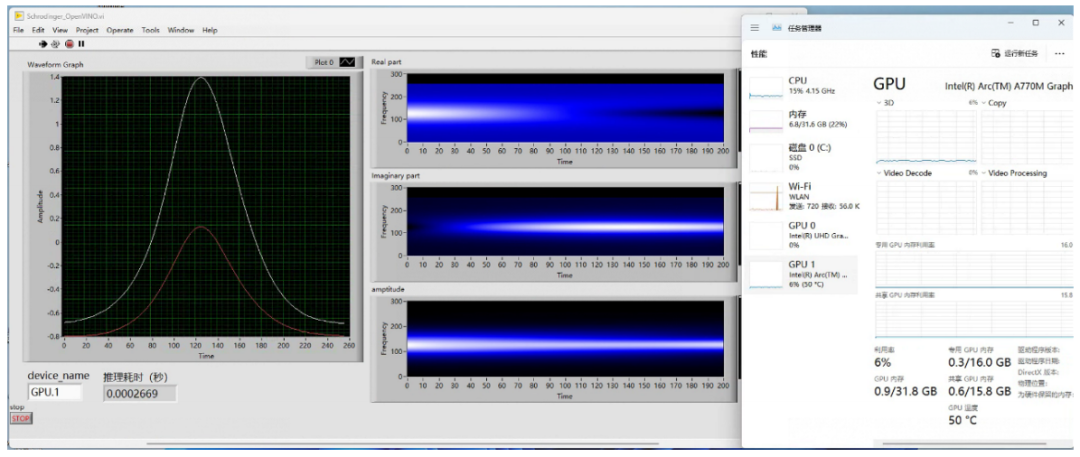
左邊的波形圖為每一個時間點的波函數實部和虛部的曲線，右邊的強度圖為所有時間點的實部、虛部和幅值分布。結果表明，使用OpenVINO推理物理信息神經網絡模型，和deepxde的結果完全一致。此外，在A770上模型也得到了最大加速，并節省了大量的cpu資源。

公司簡介

上海儀酷智能科技有限公司是國內領先的人工智能軟件提供商和機器人應用開發商，開發了低代碼可重構的人工智能定制平臺，包括基于邊緣計算的高性能、高性價比工業硬件，以及跨平臺的圖形化深度學習視覺軟件，滿足智能制造、智慧醫療、智慧教育等多個領域的定制化需求；同時為廣大院校用戶搭建了人工智能教育軟硬件平臺（語音交互套件、無人駕駛套件、機械臂套件、以及支持所有硬件的云端實驗平臺）；公司是百度、軟銀機器人、NI、Intel的戰略合作伙伴，科大訊飛創投生態圈下企業，連續多年上海交通大學優秀合作伙伴，上海市高新技術企業，姑蘇領軍人才,且入駐百度飛槳人工智能產業賦能中心，擁有70余項專利及著作權，總部位于上海，于蘇州、安慶設立分公司。

本文使用LabVIEW調用IR模型解薛定諤方程，主要使用了儀酷智能LabVIEW圖形化AI視覺工具包和LabVIEW圖形化OpenVINO工具包，大家可以在儀酷智能公司官網下載相應軟件工具包。