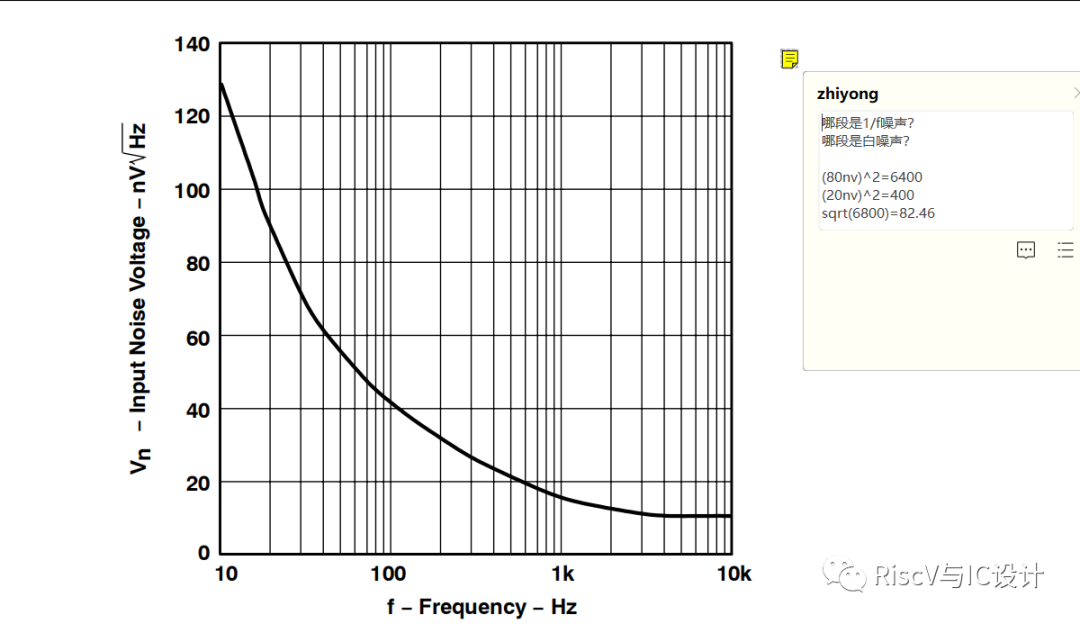
這是一個典型的運放芯片的等效輸入噪聲功率譜密度曲線,其低頻以1/f噪聲為主,隨頻率增加而快速下降,中高頻段基本為直線,以白噪聲為主,前述講的電子系統5種噪聲:散粒噪聲、熱噪聲都是白噪聲,閃爍(變)噪聲即1/f噪聲,而突發噪聲和雪崩噪聲在放大器設計里由于芯片工藝的進步,這兩類已經很小了,可以不考慮,可見放大器芯片的散粒噪聲、熱噪聲都是白噪聲,閃爍(變)噪聲即1/f噪聲剛好符合上圖 的實際測試數據,我們把運放的噪聲分為兩類:白噪聲(包括散粒噪聲、熱噪聲)和1/f噪聲,則總噪聲為

這是在特定帶寬內的噪聲功率,計算的關鍵是求出C和k^2,
而現在我們有的只是運放數據手冊上的一張噪聲功率譜密度曲線,如何從此曲線上求C和k^2?我們先做一個數字游戲:
(2)^2+( 3 )^2=4+9=13=( **3.6** )^2
(2)^2+( 5 )^2=4+25=29=( **5.39** )^2
(2)^2+( 7 )^2=4+49=53=( **7.28** )^2
(2)^2+( 10 )^2=4+100=104=( **10.2** )^2
(2)^2+( 20 )^2=4+400=404=( **20.01** )^2
大家發現了什么規律?一個大噪聲與一個小噪聲疊加時,當差別較大時,總的輸出就基本等于大噪聲,小噪聲的影響可以忽略!
那么C如何求?當頻率很高時,1/f噪聲衰減的已經可以忽略,而白噪聲的頻譜一直保持常數,所以大家廠家提供的噪聲功率譜曲線時,遠離低頻的密度數值就是C!前圖的C在10khz基本上12nv/根號HZ,現在如何求k^2 ?這里介紹一個常用的方法:
先選一個足夠低的頻率,比如上圖的10hz,對應曲線顯示130nv/根號Hz,此點的噪聲包括了白噪聲與1/f噪聲,白噪聲的C前面已經求得12nv,

現在有了C和k^2,就可以求出設計頻率范圍內的運放輸入噪聲的有效值了。
有時我們不直接求k^2,定義一個轉折頻率fnc:

-
放大器
+關注
關注
143文章
13437瀏覽量
212216 -
衰減器
+關注
關注
4文章
630瀏覽量
34165 -
運放芯片
+關注
關注
0文章
20瀏覽量
19435 -
白噪聲
+關注
關注
0文章
14瀏覽量
10478 -
熱噪聲
+關注
關注
0文章
45瀏覽量
8100
發布評論請先 登錄
相關推薦
放大器噪聲的來源

低噪聲放大器,低噪聲放大器型號參數
低噪聲設計與最佳放大器選擇
放大器的噪聲




 放大器的噪聲問題(2)
放大器的噪聲問題(2)












評論