1 算法與時(shí)間復(fù)雜度
算法(Algorithm)是求解一個(gè)問(wèn)題需要遵循的,被清楚指定的簡(jiǎn)單指令的集合。
算法一旦確定,那么下一步就要確定該算法將需要多少時(shí)間和空間等資源,如果一個(gè)算法需要一兩年的時(shí)間來(lái)完成,那么該算法的用處就不會(huì)太大。同樣如果該算法需要若干個(gè)GB的內(nèi)存,那么在大部分機(jī)器上都無(wú)法使用。
一個(gè)算法的評(píng)價(jià)主要從時(shí)間復(fù)雜度和空間復(fù)雜度來(lái)考慮。
而時(shí)間復(fù)雜度是一個(gè)函數(shù),定性描述該算法的運(yùn)行時(shí)間,通常用大O符號(hào)表示。
常見(jiàn)的時(shí)間復(fù)雜度有O(1),O(logn),O(n),O(n^2),O(2^n)...等
那么一個(gè)算法的時(shí)間復(fù)雜度如何計(jì)算呢,下面接著講。
2 時(shí)間復(fù)雜度計(jì)算
2.1 第一個(gè)時(shí)間復(fù)雜度計(jì)算
首先我們定義算法中的語(yǔ)句執(zhí)行次數(shù)稱(chēng)為語(yǔ)句頻度或時(shí)間頻度為T(mén)(n)。即T(n)表示程序的執(zhí)行次數(shù) 。
首先我們看看如下的方法1執(zhí)行多少次;
public int method1(){
System.out.println("java技術(shù)指北 等你來(lái)"); //執(zhí)行1次
return 0; //執(zhí)行1次
}
沒(méi)錯(cuò),它內(nèi)部一共執(zhí)行2次。
那么我們來(lái)看下面的方法2執(zhí)行幾次:
public int method2(int n){
for(int i = 0; i< n ; i++){
//i = 0 執(zhí)行1次,i< n 執(zhí)行n+1次,i++執(zhí)行n次
System.out.println("java技術(shù)指北 等你來(lái)"); //輸出語(yǔ)句執(zhí)行n次
}
return 1; //return 執(zhí)行一次
}
對(duì),它一共執(zhí)行了 3n+3 次。
那么對(duì)于方法1就有 T(n) = 2;
對(duì)于方法2就有 T(n) = 3n + 3;
實(shí)際的代碼肯定比示例中的代碼復(fù)雜得多,去統(tǒng)計(jì)代碼的執(zhí)行次數(shù)顯然不可能,所以算法一般使用T(n)的漸進(jìn)估算值來(lái)反映代碼的執(zhí)行速度。而這個(gè)估算值我們用"時(shí)間復(fù)雜度"來(lái)表示。
所以針對(duì)方法1和方法2,如何根據(jù)T(n)估算出時(shí)間復(fù)雜度
過(guò)程如下:
- 對(duì)于 T(n) = 2 ,由于T(n)是一個(gè)常數(shù),那么時(shí)間復(fù)雜度可以直接估算為 1 。所以T(n) = 2 的時(shí)間復(fù)雜度為 1。用標(biāo)準(zhǔn)的時(shí)間復(fù)雜度函數(shù)表示就是 O(1)。
- 對(duì)于T(n) = 3n + 3 ,隨著n值得不斷增長(zhǎng),常數(shù)3相對(duì)于3n來(lái)說(shuō)可以忽略不計(jì)。而系數(shù)一般也會(huì)估算成1。相當(dāng)于去掉了系數(shù)和常數(shù),則該時(shí)間復(fù)雜度為n。用時(shí)間復(fù)雜度函數(shù)表示就是O(n)。
- 依次推廣到如下多項(xiàng)式中:對(duì)于T(n) = 3n^2 + 3n + 3. 隨著n值得不斷增大,多項(xiàng)式后面的項(xiàng)的增長(zhǎng)就遠(yuǎn)沒(méi)有n^2的增長(zhǎng)大,可以直接舍棄低階項(xiàng)和常數(shù)項(xiàng),則只保留n的次方數(shù)最大的那一項(xiàng),所以它的時(shí)間復(fù)雜度就為O(n^3)。
小結(jié)一下,以上三個(gè)表達(dá)式的時(shí)間復(fù)雜度表示如下
| 表達(dá)式 | 時(shí)間復(fù)雜度 |
|---|---|
| T(n) = 2 | O(1) |
| T(n) = 3n + 3 | O(n) |
| T(n) = 3n^2 + 3n + 3 | O(n^2) |
總結(jié)以上規(guī)律:
- T(n)是常數(shù):時(shí)間復(fù)雜度為O(1)
- T(n)不是常數(shù):時(shí)間復(fù)雜度為O(T(n)的最高次項(xiàng)并且去掉最高次項(xiàng)的系數(shù))
2.2 常見(jiàn)循環(huán)的復(fù)雜度
下面方法1的時(shí)間復(fù)雜度為 O(1):
//時(shí)間復(fù)雜度為 O(1)
public void m1(){
System.out.println("java技術(shù)指北 等你來(lái)");
System.out.println("操千曲而后曉聲,觀千劍而后識(shí)器");
...
System.out.println("java技術(shù)指北 非你莫屬");
}
下面方法2的時(shí)間復(fù)雜度為 O(n):
//時(shí)間復(fù)雜度為 O(n)
public int method2(int n){
for(int i = 0; i < n ; i++){
System.out.println("java技術(shù)指北 等你來(lái)");
}
return 1;
}
下面方法3 時(shí)間復(fù)雜度為 O(n^2):
//時(shí)間復(fù)雜度為 O(n^2)
public void method3(int n){
for(int i = 0; i < n ; i++){
for(int j = 0 ; j < i ; j ++){
System.out.println("java技術(shù)指北 等你來(lái)");
}
}
}
下面方法4的時(shí)間復(fù)雜度為 O(n^2):
以下方法4中第一個(gè)循環(huán)執(zhí)行Q其時(shí)間復(fù)雜度為為O(n^2)
第二個(gè)循環(huán)時(shí)間復(fù)雜度為O(n)
則整個(gè)方法的時(shí)間復(fù)雜度要舍棄變化小的部分,最終的時(shí)間復(fù)雜度為O(n^2)
//時(shí)間復(fù)雜度為 O(n^2)
public int method4(int n){
for(int i = 0; i < n ; i++){
for(int j = 0 ; j < i ; j ++){
System.out.println("java技術(shù)指北 等你來(lái)");
}
}
for(int i = 0; i < n ; i++){
System.out.println("java技術(shù)指北 等你來(lái)");
}
return 1;
}
方法5的時(shí)間復(fù)雜度依然為O(n):
由于隨著n的增大,方法5種執(zhí)行次數(shù)最多的是else后面的循環(huán),所以會(huì)取執(zhí)行次數(shù)最多的部分來(lái)計(jì)算時(shí)間復(fù)雜度。
//時(shí)間復(fù)雜度為O(n)
public int method5(int n){
if( n < 100){
for(int i = 0; i < n ; i++){
for(int j = 0 ; j < n ; j ++){
System.out.println("java技術(shù)指北 等你來(lái)");
}
}
}else{
for(int i = 0; i < n ; i++){
System.out.println("java技術(shù)指北 等你來(lái)");
}
}
return 1;
}
2.3 其他時(shí)間復(fù)雜度計(jì)算
分析下面方法6的時(shí)間復(fù)雜度
public void method6(int n){
for(int i = 0; i < n ; i++){
for(int j = 0 ; j < n ; j ++){
System.out.println("java技術(shù)指北 等你來(lái)");
}
}
}
方法6執(zhí)行分析
i=0 輸出語(yǔ)句執(zhí)行 n 次
i=1 輸出語(yǔ)句執(zhí)行 n-1 次
i=2 輸出語(yǔ)句執(zhí)行 n-2 次
...
...
i=n-2 輸出語(yǔ)句執(zhí)行 2 次
i=n-1 輸出語(yǔ)句執(zhí)行 1 次
總執(zhí)行次數(shù)就是
T(n) = n + (n-1) + (n-2) ... + 2 + 1
= n(n+1)/2 = 1/2*n^2 =
則其時(shí)間復(fù)雜度為O(n^2)
下面我們?cè)诳捶椒?的時(shí)間復(fù)雜度
public void method7(int n){
int i = 1;
while(i< n)
{
i = i * 2;
}
}
執(zhí)行情況分析:
n = 2 的時(shí)候執(zhí)行1次 即 T(2) = 1
n = 4 的時(shí)候執(zhí)行2次 即 T(4) = 2
n = 8 的時(shí)候執(zhí)行3次 即 T(8) = 3
n = 16 的時(shí)候執(zhí)行4次 即 T(16) = 4
我們發(fā)現(xiàn)如下規(guī)律
n = 2 的時(shí)候有 2^T(2) = 2
n = 4 的時(shí)候有 2^T(4) = 4
n = 8 的時(shí)候有 2^T(8) = 8
n = 16 的時(shí)候有 2^T(16) = 16
n = 32 的時(shí)候有 2^T(32) = 32
n = n 的時(shí)候有 2^T(n) = n
如果要把T(n)放到等式左邊那么
那么時(shí)間復(fù)雜度就是
再去掉底數(shù)2 則時(shí)間復(fù)雜度為
3 時(shí)間復(fù)雜度排序
我們分析了以上幾種簡(jiǎn)單循環(huán)的時(shí)間復(fù)雜度,那么既然時(shí)間復(fù)雜度是用來(lái)表示算法的執(zhí)行效率的,我們對(duì)一般常見(jiàn)的時(shí)間復(fù)雜度進(jìn)行如下排序(由快到慢)。
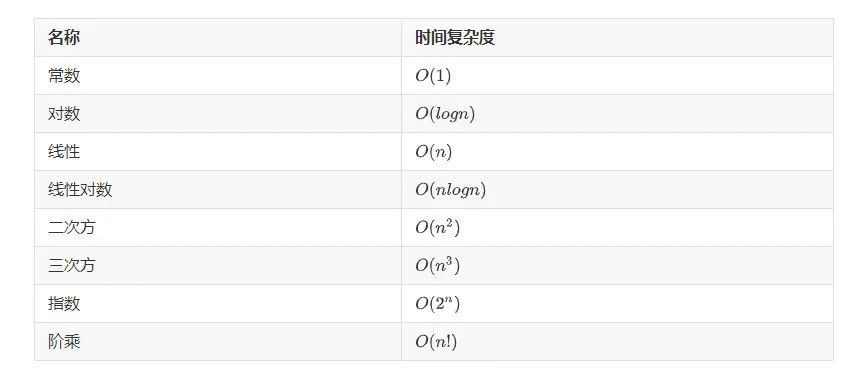
timeComplexitiesOrder.jpg
我們?cè)儆们€(xiàn)圖看一下時(shí)間復(fù)雜度。
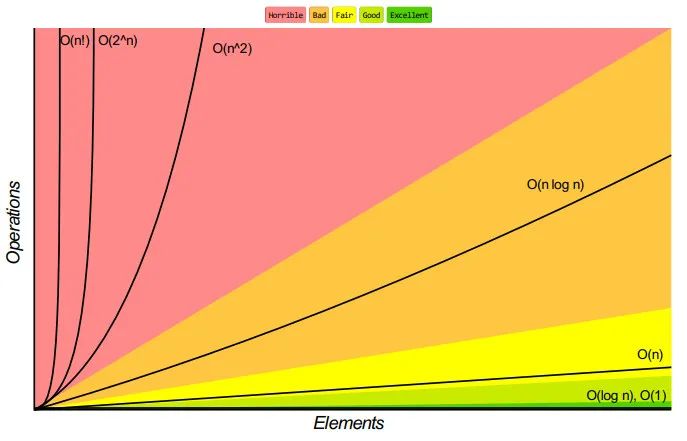
從圖中也可以看出,隨著元素變多,指數(shù)、階乘級(jí)別的增長(zhǎng)是最快的。顯而易見(jiàn)其執(zhí)行效率最低。
4 時(shí)間復(fù)雜度推算
最后我們計(jì)算一下如下遞推關(guān)系的算法的時(shí)間復(fù)雜度
T(n)= T(n-1) + n,其中 T(0) = 1,求T(n)的時(shí)間復(fù)雜度?
我們可以將n-1 帶入上面的公式,得到 T(n-1) = T(n-2) + (n-1)
再將T(n-1) 的表達(dá)式帶入到T(n)的表達(dá)式
再依次將n-2 ,n-3...帶入到公式中,其演算結(jié)果如下。
T(n)= T(n-1) + n
= T(n-2) + (n-1) + n
= T(n-3) +(n-2) + (n-1) + n
......
= T(2) + 3 + ......(n-2) + (n-1) + n
= T(1) + 2 + 3 + ......(n-2) + (n-1) + n
= T(0) + 1 + 2 + 3 + ......(n-2) + (n-1) + n
= 1 + 1 + 2 + 3 + ...... + (n-1) +n
最終我們得到T(n) 的時(shí)間復(fù)雜度為O(n^2)
總結(jié)
本篇介紹了時(shí)間復(fù)雜度以及如何計(jì)算時(shí)間復(fù)雜度,相信你已經(jīng)掌握了吧。
-
內(nèi)存
+關(guān)注
關(guān)注
8文章
3004瀏覽量
73900 -
程序
+關(guān)注
關(guān)注
116文章
3778瀏覽量
80859 -
機(jī)器
+關(guān)注
關(guān)注
0文章
779瀏覽量
40691 -
函數(shù)
+關(guān)注
關(guān)注
3文章
4308瀏覽量
62444
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
PCB與PCBA工藝復(fù)雜度的量化評(píng)估與應(yīng)用初探!

數(shù)據(jù)結(jié)構(gòu):第1章緒論第5講-計(jì)算時(shí)間復(fù)雜度舉例(1)#結(jié)構(gòu)數(shù)據(jù)

數(shù)據(jù)結(jié)構(gòu):第1章緒論第5講-計(jì)算時(shí)間復(fù)雜度舉例(2)#結(jié)構(gòu)數(shù)據(jù)
JEM軟件復(fù)雜度的增加情況
時(shí)間復(fù)雜度是指什么
各種排序算法的時(shí)間空間復(fù)雜度、穩(wěn)定性
圖像復(fù)雜度對(duì)信息隱藏性能影響分析
深度剖析時(shí)間復(fù)雜度
如何求遞歸算法的時(shí)間復(fù)雜度
如何求遞歸算法的時(shí)間復(fù)雜度
常見(jiàn)機(jī)器學(xué)習(xí)算法的計(jì)算復(fù)雜度
算法時(shí)空復(fù)雜度分析實(shí)用指南1
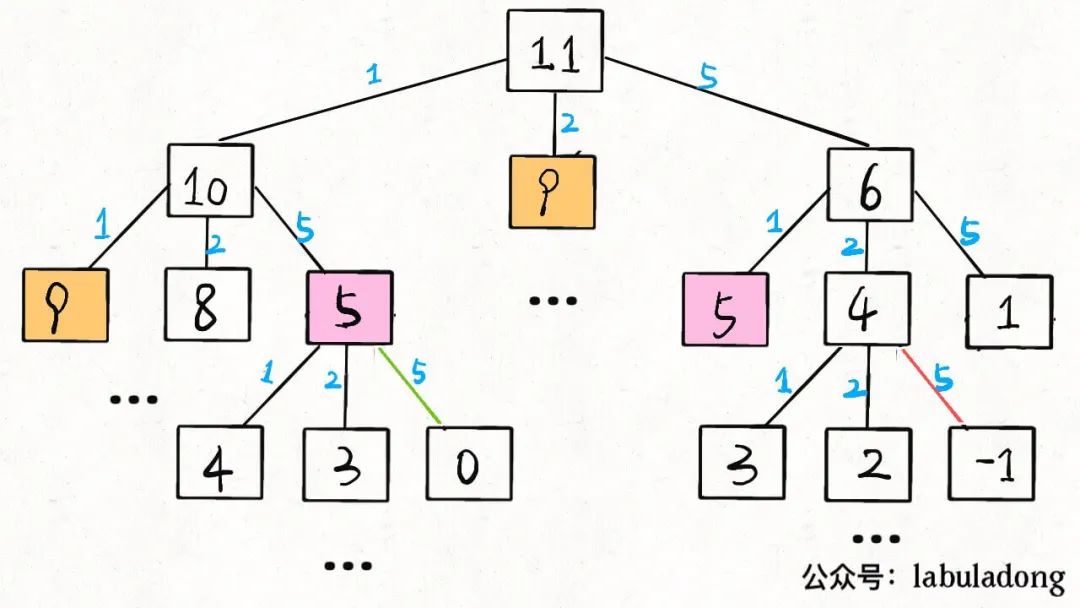
算法時(shí)空復(fù)雜度分析實(shí)用指南2
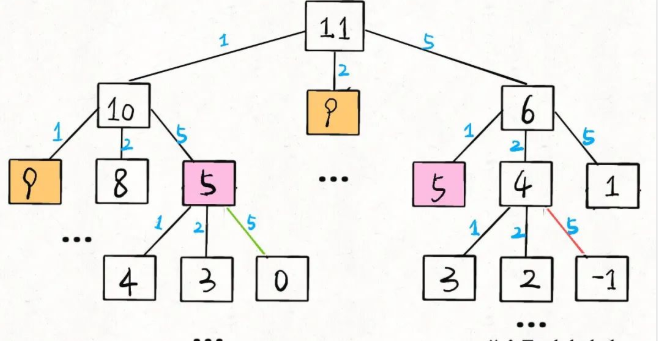
算法時(shí)空復(fù)雜度分析實(shí)用指南(上)

算法時(shí)空復(fù)雜度分析實(shí)用指南(下)





 如何計(jì)算時(shí)間復(fù)雜度
如何計(jì)算時(shí)間復(fù)雜度










評(píng)論