在機器學任務中,確定變量間的因果關系(causality)可能是一個具有挑戰性的步驟,但它對于建模工作非常重要。本文將總結有關貝葉斯概率(Bayesian probabilistic)因果模型(causal models)的概念,然后提供一個Python實踐教程,演示如何使用貝葉斯結構學習來檢測因果關系。
1. 背景
在許多領域,如預測、推薦系統、自然語言處理等,使用機器學習技術已成為獲取有用觀察和進行預測的標準工具。
雖然機器學習技術可以實現良好的性能,但提取與目標變量的因果關系并不直觀。換句話說,就是:哪些變量對目標變量有直接的因果影響? 機器學習的一個分支是貝葉斯概率圖模型(Bayesian probabilistic graphical models),也稱為貝葉斯網絡(Bayesian networks, BN),可用于確定這些因果因素。
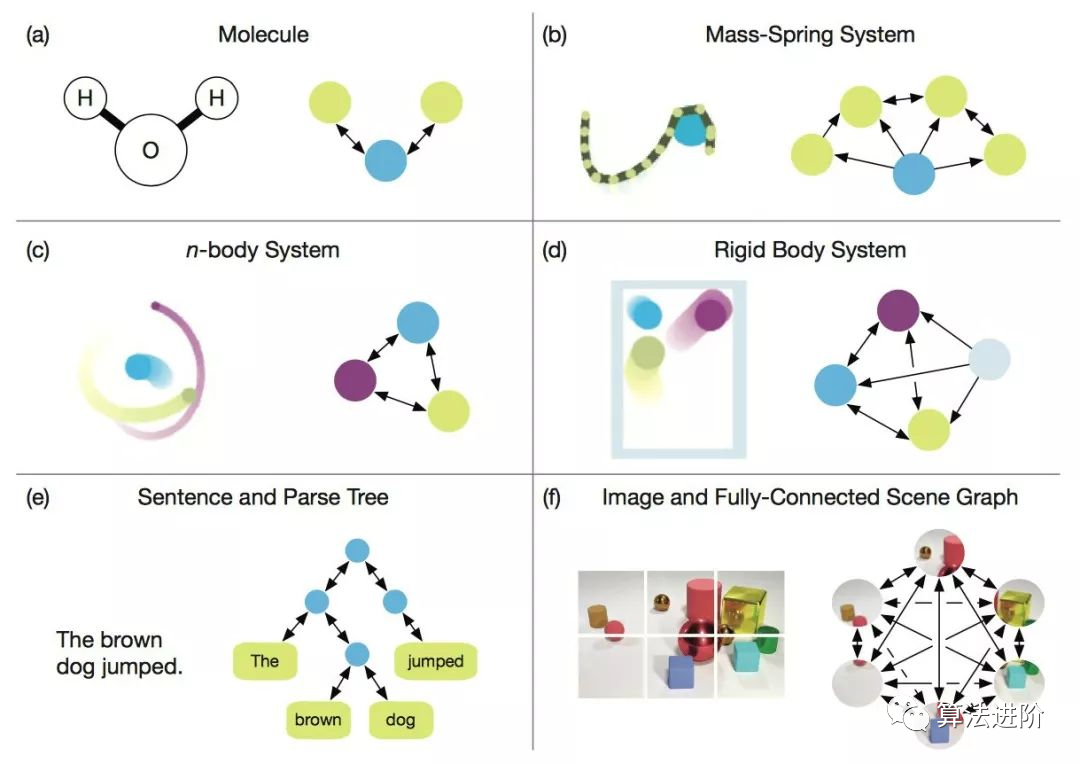
在我們深入討論因果模型的技術細節之前,讓我們先復習一些術語:包括"相關性"(correlation)和"關聯性"(association)。 注意,相關性或關聯性并不等同于因果關系。換句話說,兩個變量之間的觀察到的關系并不一定意味著一個導致了另一個。從技術上講,相關性指的是兩個變量之間的線性關系,而關聯性則指的是兩個(或更多)變量之間的任何關系。而因果關系則意味著一個變量(通常稱為預測變量或自變量)導致另一個變量(通常稱為結果變量或因變量)。接下來,我將通過示例簡要描述相關性和關聯性。
1.1. 相關性
皮爾遜相關系數(Pearson correlation coefficient)是最常用的相關系數。系數強度由r表示,取值區間-1到1。 在使用相關性時,有三種可能的結果:
正相關:兩個變量之間存在一種關系,即兩個變量同時朝同一方向移動。
負相關:兩個變量之間存在一種關系,即一個變量增加與另一個變量減少相關聯。
無相關性:當兩個變量之間沒有關系時。
正相關的一個示例如圖 1 所示,圖中展示了巧克力消費與每個國家的諾貝爾獎獲得者數量之間的關系。
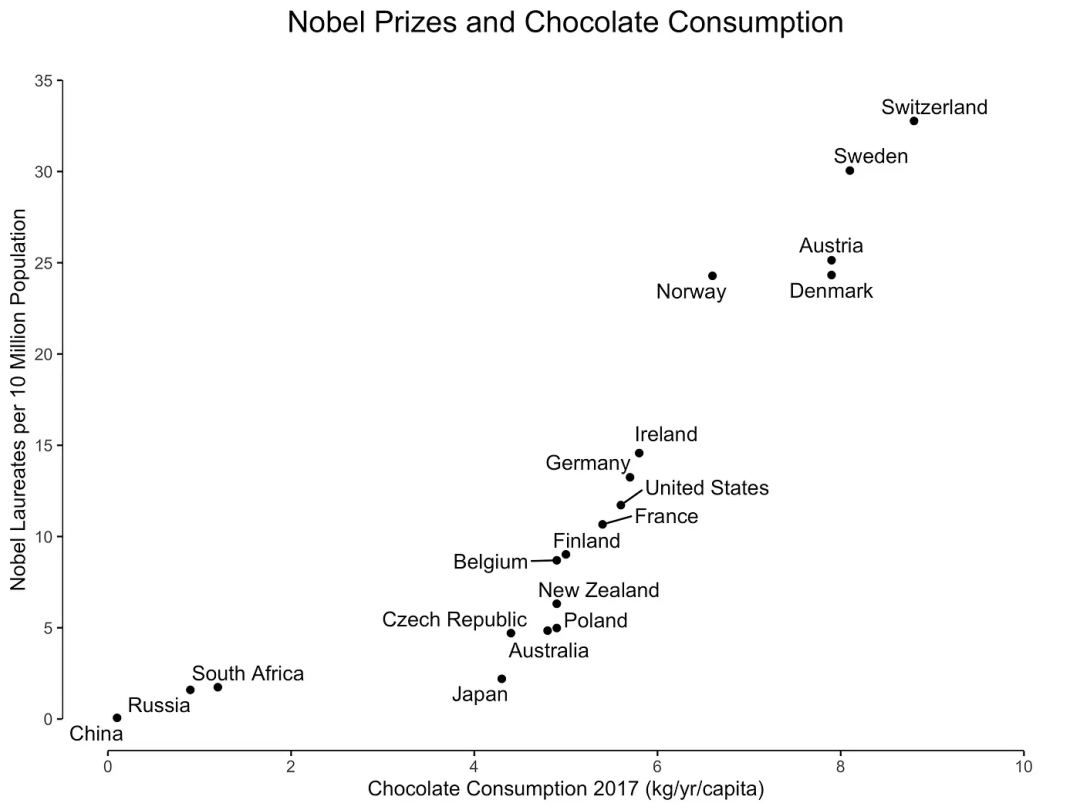
圖1:巧克力消費與諾貝爾獎獲得者之間的相互關系 巧克力消費可能意味著諾貝爾獎獲得者增加。或者反過來,諾貝爾獎獲得者的增加同樣可能導致巧克力消費增加。盡管存在強烈的相關性,但更有可能的是未觀察到的變量,如社會經濟地位或教育系統質量,可能導致巧克力消費和諾貝爾獎獲得者數量的增加。 換句話說,我們仍然不知道這種關系是否是因果關系。但這并不意味著相關性本身沒有用處,它只是有著不同的目的。 相關性本身并不意味著因果關系,因為統計關系并不能唯一限制因果關系。
1.1.2. 關聯性?
當我們談論關聯性時,我們指的是一個變量的某些值傾向于與另一個變量的某些值共同出現。 從統計學的角度來看,有許多關聯性測量方法,例如卡方檢驗(chi-square test)、費舍爾精確檢驗(Fisher exact test)、超幾何檢驗(hypergeometric test)等。它們通常用于其中一個或兩個變量為有序(ordinal)或名義(nominal)變量的情況。 注意:相關性是一個技術術語,而關聯性不是,因此在統計學中對其含義并不總是一致的。這意味著在使用這些術語時,明確說明其含義總是一個好的做法。 為了舉例說明,我將使用超幾何檢驗來演示是否存在兩個變量之間的關聯性,使用泰坦尼克號數據集。 泰坦尼克號數據集在許多機器學習示例中都有使用,眾所周知,性別(女性)是生存的一個很好的預測因子。讓我演示一下如何計算幸存和女性之間的關聯性。 首先,安裝 bnlearn 庫,并僅加載泰坦尼克號數據集。問:女性幸存的概率是多少?
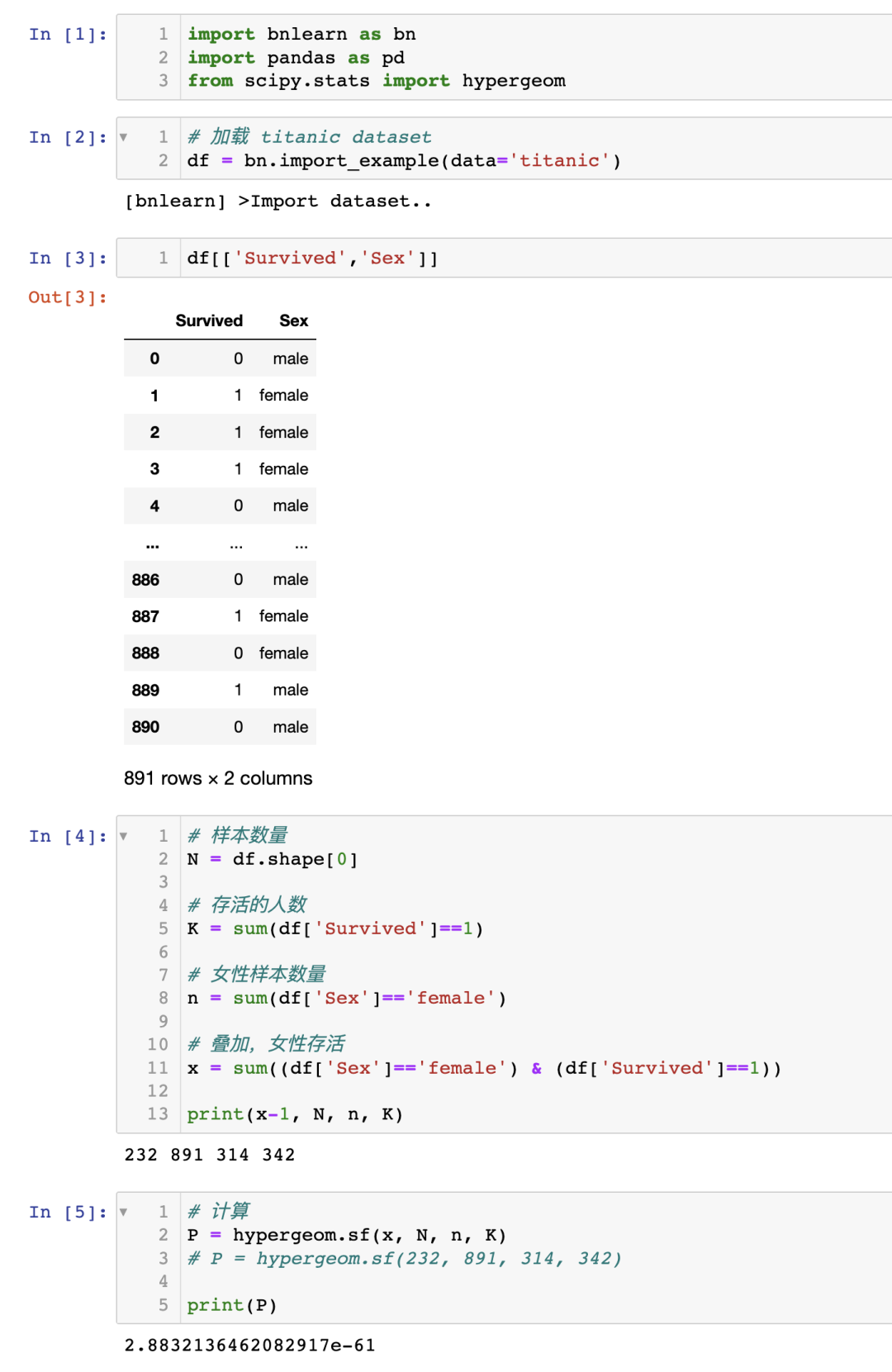
零假設:幸存與性別之間沒有關系。超幾何檢驗使用超幾何分布來測量離散概率分布的統計顯著性。在這個例子中,是總體大小(891),是總體中成功狀態的數量(342), 是樣本大小/抽樣次數(314),是樣本中成功的數量(233)。
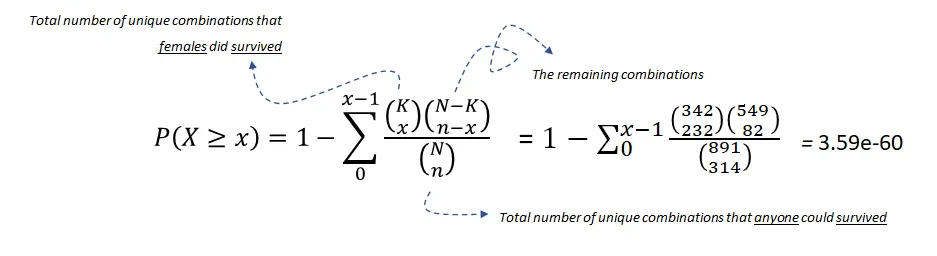
方程 1:使用超幾何檢驗測試幸存與女性之間的關聯性
在的顯著性水平下,我們可以拒絕零假設,因此可以說幸存和女性之間存在統計顯著的關聯。 注意,關聯性本身并不意味著因果關系。我們需要區分邊際關聯(marginal)和條件關聯(conditional)。后者是因果推斷的關鍵構建模塊。
2. 因果關系
什么是因果關系(causality)? 因果關系意味著一個independent變量導致另一個dependent變量,并由 Reichenbach(1956)如下所述:
如果兩個隨機變量 和 在統計上相關(),那么要么(a)導致 ,(b)導致 ,或者(c)存在一個第三個變量 同時導致 和。此外,給定的條件下, 和 變得獨立,即 。
這個定義被納入貝葉斯圖模型中。
貝葉斯圖模型又稱貝葉斯網絡、貝葉斯信念網絡、Bayes Net、因果概率網絡和影響圖。都是同一技術,不同的叫法。
為了確定因果關系,我們可以使用貝葉斯網絡(BN)。 讓我們從圖形開始,并可視化 Reichenbach 所描述的三個變量之間的統計依賴關系(參見圖 2)。節點對應變量,有向邊(箭頭)表示依賴關系或條件分布。
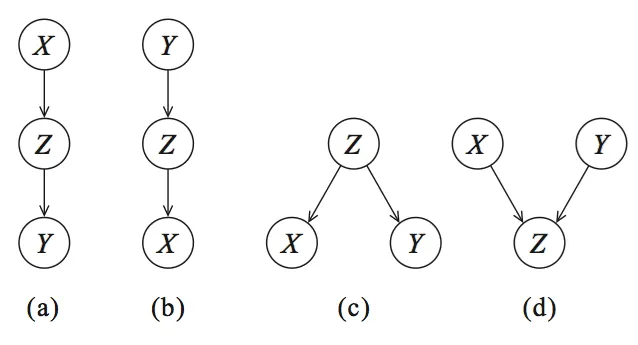
圖 2:有向無環圖(DAG)編碼條件獨立性。(a、b、c)是等價類。(a、b)級聯,(c)共同父節點,(d)是具有 V 結構的特殊類別 可以創建四個圖:(a、b)級聯,(c)共同父節點和(d)V 結構,這些圖構成了貝葉斯網絡的基礎。 但是我們如何確定什么是造成什么的原因?(how can we tell what causes what?) 確定因果關系的概念思想是通過將一個節點保持不變,然后觀察其影響來確定因果關系的方向,即哪個節點影響哪個節點。 舉個例子,讓我們看一下圖 2 中的有向無環圖 DAG(a),它描述了 由 引起, 由引起。如果我們現在將 保持不變,如果這個模型是正確的, 不應該發生變化。每個貝葉斯網絡都可以用這四個圖來描述,并且通過概率論(參見下面的部分),我們可以將這些部分組合起來。
需要注意的是,貝葉斯網絡是有向無環圖(Directed Acyclic Graph, DAG),而 DAG 是具有因果性的。這意味著圖中的邊是有向的,并且沒有(反饋)循環(無環)。
2.1. 概率論
概率論,或者更具體地說貝葉斯定理或貝葉斯規則,構成了貝葉斯網絡的基礎。 貝葉斯規則用于更新模型信息,數學上表示如下方程式:
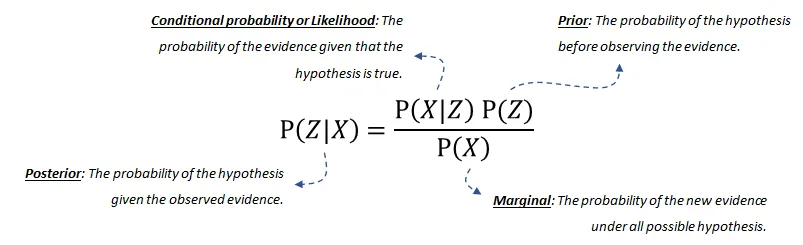
方程式由四個部分組成:
后驗概率(posterior probability)是給定 發生的概率。
條件概率(conditional probability)或似然是在假設成立的情況下,證據發生的概率。這可以從數據中推導出來。
我們的先驗(prior)信念是在觀察到證據之前,假設的概率。這也可以從數據或領域知識中推導出來。
最后,邊際(marginal)概率描述了在所有可能的假設下新證據發生的概率,需要計算。如果您想了解更多關于(分解的)概率分布或貝葉斯網絡的聯合分布的詳細信息,請閱讀這篇博客[6]。
3. 貝葉斯結構學習用于估計 DAG
通過結構學習,我們希望確定最能捕捉數據集中變量之間因果依賴關系的圖結構。 換句話說:什么樣的 DAG 最適合數據? 一種樸素的方法是簡單地創建所有可能的圖結構組合,即創建成十個、幾百個甚至幾千個不同的 DAG,直到所有組合都耗盡為止。 然后,可以根據數據的適應度對每個 DAG 進行評分。 最后,返回得分最高的 DAG。 在僅有變量X的情況下,可以創建如圖 2 所示的圖形以及更多的圖形,因為不僅可以是 X>Z>Y(圖 2a),還可以是 Z>X>Y 等等。變量X可以是布爾值(True 或 False),也可以有多個狀態。 DAG 的搜索空間在最大化得分的變量數量上呈指數增長。這意味著在大量節點的情況下,窮舉搜索是不可行的,因此已經提出了各種貪婪策略來瀏覽 DAG 空間。 通過基于優化的搜索方法,可以瀏覽更大的 DAG 空間。這種方法需要一個評分函數和一個搜索策略。 常見的評分函數是給定訓練數據的結構的后驗概率,例如BIC或BDeu。
BIC是貝葉斯信息準則(Bayesian Information Criterion)的縮寫。它是一種用于模型選擇的統計量,可以用于比較不同模型的擬合能力。BIC值越小,表示模型越好。在貝葉斯網絡中,BIC是一種常用的評分函數之一,用于評估貝葉斯網絡與數據的擬合程度。
BDeu是貝葉斯-狄利克雷等價一致先驗(Bayesian-Dirichlet equivalent uniform prior)的縮寫。它是一種常用的評分函數之一,用于評估貝葉斯網絡與數據的擬合程度。BDeu評分函數基于貝葉斯-狄利克雷等價一致先驗,該先驗假設每個變量的每個可能狀態都是等可能的。
在我們開始示例之前,了解何時使用哪種技術總是很好的。在搜索整個 DAG 空間并找到最適合數據的圖形的過程中,有兩種廣泛的方法。
基于評分的結構學習
基于約束的結構學習
3.1. 基于評分的結構學習
基于評分的方法有兩個主要組成部分:
搜索算法用于優化所有可能的 DAG 搜索空間;例如 ExhaustiveSearch、Hillclimbsearch、Chow-Liu 等。
評分函數指示貝葉斯網絡與數據的匹配程度。常用的評分函數是貝葉斯狄利克雷分數,如 BDeu 或 K2,以及貝葉斯信息準則(BIC,也稱為 MDL)。
下面描述了四種常見的基于評分的方法:
ExhaustiveSearch,顧名思義,對每個可能的 DAG 進行評分并返回得分最高的 DAG。這種搜索方法僅適用于非常小的網絡,并且阻止高效的局部優化算法始終找到最佳結構。因此,通常無法找到理想的結構。然而,如果只涉及少數節點(即少于 5 個左右),啟發式搜索策略通常會產生良好的結果。
Hillclimbsearch 是一種啟發式搜索方法,可用于使用更多節點的情況。HillClimbSearch 實施了一種貪婪的局部搜索,從 DAG“start”(默認為斷開的 DAG)開始,通過迭代執行最大化增加評分的單邊操作。搜索在找到局部最大值后終止。
Chow-Liu 算法是一種特定類型的基于樹的方法。Chow-Liu 算法找到最大似然樹結構,其中每個節點最多只有一個父節點。通過限制為樹結構,可以限制復雜性。
Tree-augmented Naive Bayes(TAN)算法也是一種基于樹的方法,可用于建模涉及許多不確定性的龐大數據集的各種相互依賴特征集。
3.2. 基于約束的結構學習
一種不同但相當直觀的構建 DAG 的方法是使用假設檢驗(如卡方檢驗統計量)來識別數據集中的獨立性。 這種方法依賴于統計檢驗和條件假設,以學習模型中變量之間的獨立性。 卡方檢驗的值是觀察到的計算卡方統計量的概率,假設空設為 和 在給定 的條件下是獨立的。這可以用于在給定顯著性水平的情況下進行獨立判斷。 約束性方法的一個示例是 PC 算法,它從一個完全連接的圖開始,并根據測試的結果刪除邊,如果節點是獨立的,直到達到停止準則。
4. 實踐:基于bnlearn 庫
下面介紹Python中的學習貝葉斯網絡圖形結構的庫——bnlearn。 bnlearn能解決一些挑戰,如:
結構學習:給定數據:估計捕捉變量之間依賴關系的 DAG。
參數學習:給定數據和 DAG:估計各個變量的(條件)概率分布。
推斷:給定學習的模型:確定查詢的精確概率值。
bnlearn 相對于其他貝葉斯分析實現有如下優勢:
基于 pgmpy 庫構建
包含最常用的貝葉斯管道
簡單直觀
開源
詳細文檔
4.1. 在灑水器數據集中進行結構學習
讓我們從一個簡單而直觀的示例開始,以演示結構學習的工作原理。 假設你在后院安裝了一個灑水系統,并且在過去的 1000 天里,你測量了四個變量,每個變量有兩個狀態:雨(是或否),多云(是或否),灑水系統(開啟或關閉)和濕草(是或否)。 下面,導入 bnlearn 庫,加載灑水器數據集,并確定哪個 DAG 最適合該數據。
使用 bnlearn 庫,用幾行代碼就能確定因果關系。
請注意,灑水器數據集已經過處理,沒有缺失值,所有值都處于 1 或 0 的狀態。
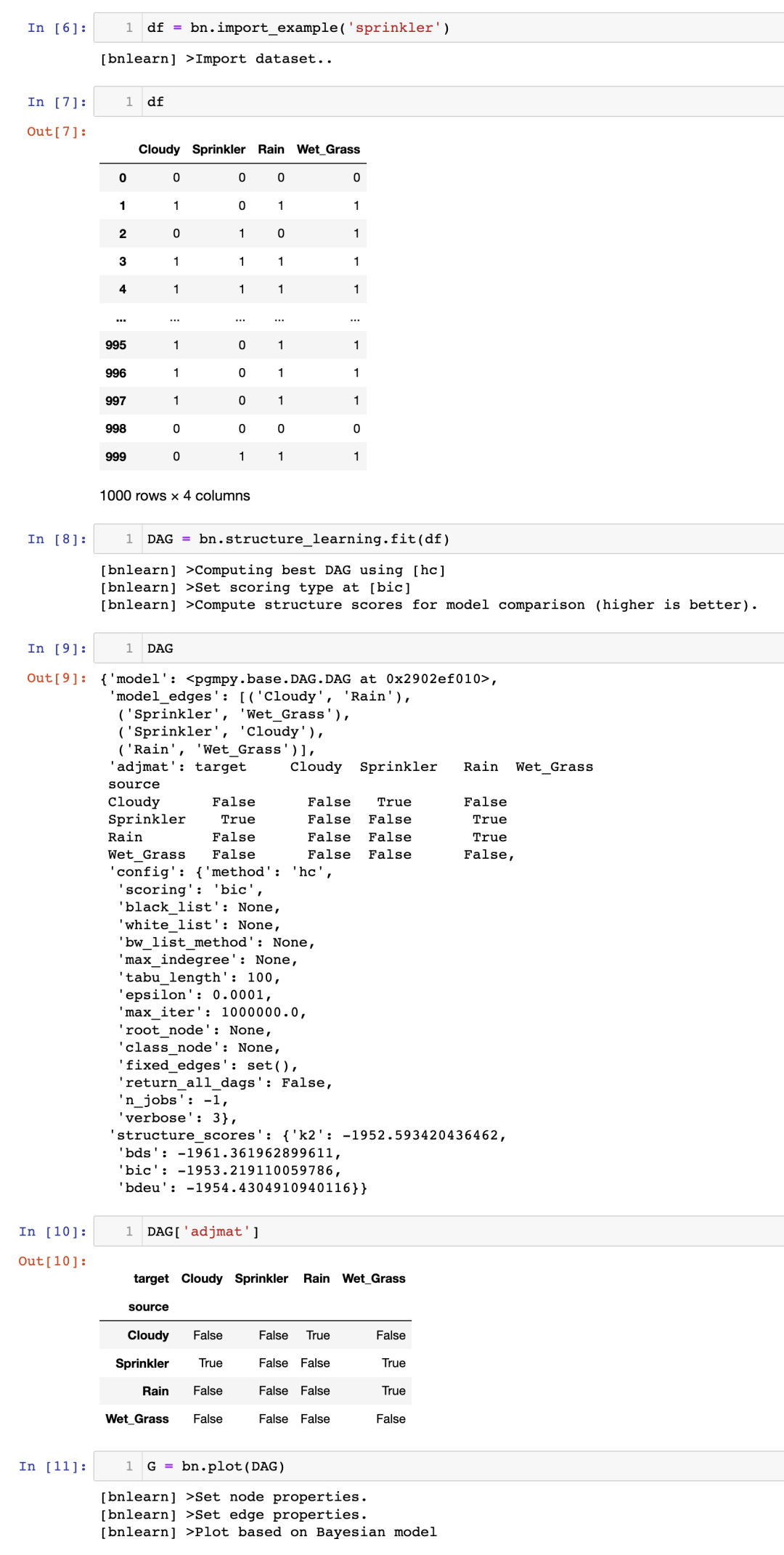
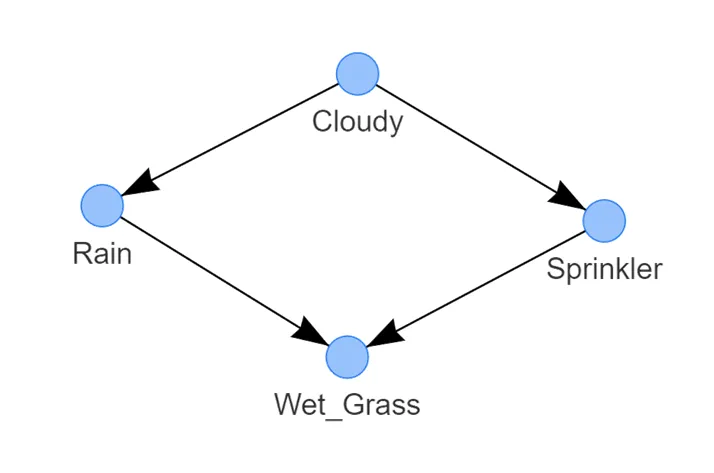
圖 3:灑水器系統的最佳 DAG 示例。它表示以下邏輯:草地潮濕的概率取決于灑水器和雨水。灑水器打開的概率取決于多云的狀態。下雨的概率取決于多云的狀態 這樣,我們有了如圖 3 所示的學習到的結構。檢測到的 DAG 由四個通過邊連接的節點組成,每條邊表示一種因果關系。
濕草的狀態取決于兩個節點,即雨水和灑水器;
雨水的狀態由多云的狀態決定;?
?而灑水器的狀態也由多云的狀態決定。
這個 DAG 表示了(因式分解的)概率分布,其中 S 是灑水器的隨機變量,R 是雨水的隨機變量,G 是濕草的隨機變量,C 是多云的隨機變量。 通過檢查圖形,很快就會發現模型中唯一的獨立變量是 C。其他變量都取決于多云、下雨和/或灑水器的概率。 一般來說,貝葉斯網絡的聯合分布是每個節點在給定其父節點的條件下的條件概率的乘積: bnlearn 在結構學習方面的默認設置是使用hillclimbsearch方法和BIC評分。 值得注意的是,可以指定不同的方法和評分類型。請參考下面的示例以指定搜索和評分類型:
# 'hc' or 'hillclimbsearch' model_hc_bic = bn.structure_learning.fit(df, methodtype='hc', scoretype='bic') model_hc_k2 = bn.structure_learning.fit(df, methodtype='hc', scoretype='k2') model_hc_bdeu = bn.structure_learning.fit(df, methodtype='hc', scoretype='bdeu') # 'ex' or 'exhaustivesearch' model_ex_bic = bn.structure_learning.fit(df, methodtype='ex', scoretype='bic') model_ex_k2 = bn.structure_learning.fit(df, methodtype='ex', scoretype='k2') model_ex_bdeu = bn.structure_learning.fit(df, methodtype='ex', scoretype='bdeu') # 'cs' or 'constraintsearch' model_cs_k2 = bn.structure_learning.fit(df, methodtype='cs', scoretype='k2') model_cs_bdeu = bn.structure_learning.fit(df, methodtype='cs', scoretype='bdeu') model_cs_bic = bn.structure_learning.fit(df, methodtype='cs', scoretype='bic') # 'cl' or 'chow-liu' (requires setting root_node parameter) model_cl = bn.structure_learning.fit(df, methodtype='cl', root_node='Wet_Grass') 盡管灑水器數據集的檢測到的 DAG 具有啟示性,并顯示了數據集中變量的因果依賴關系,但它并不能讓你提出各種問題,例如:
如果灑水器關閉,草地濕潤的概率有多大?
如果灑水器關閉且多云,下雨的概率有多大?
在灑水器數據集中,根據你對世界的了解和邏輯思考,結果可能是顯而易見的。但是,一旦你擁有更大、更復雜的圖形,可能就不再那么明顯了。 通過所謂的推斷,我們可以回答“如果我們做了 會怎樣”類型的問題,這些問題通常需要進行控制實驗和明確的干預才能回答。
4.2. 如何進行推斷?
要進行推斷,我們需要兩個要素:DAG 和條件概率表(Conditional Probabilistic Tables, CPTs)。 此時,我們已經將數據存儲在數據框(df)中,并且已經計算出描述數據結構的 DAG。需要使用參數學習計算 CPTs,以定量地描述每個節點與其父節點之間的統計關系。 讓我們首先進行參數學習,然后再回到推斷的過程中。
4.2.1. 參數學習
參數學習是估計條件概率表(CPTs)的值的任務。 bnlearn 庫支持離散和連續節點的參數學習:
最大似然估計是使用變量狀態出現的相對頻率進行的自然估計。在對貝葉斯網絡進行參數估計時,數據不足是一個常見問題,最大似然估計器存在對數據過擬合的問題。換句話說,如果觀察到的數據對于基礎分布來說不具有代表性(或者太少),最大似然估計可能會相差甚遠。例如,如果一個變量有 3 個可以取 10 個狀態的父節點,那么狀態計數將分別針對個父節點配置進行。這使得最大似然估計對學習貝葉斯網絡參數非常脆弱。減輕最大似然估計過擬合的一種方法是貝葉斯參數估計。
貝葉斯估計從已存在的先驗 CPTs 開始,這些 CPTs 表示在觀察到數據之前我們對變量的信念。然后,使用觀察數據的狀態計數來更新這些“先驗”。可以將先驗視為偽狀態計數,在歸一化之前將其添加到實際計數中。一個非常簡單的先驗是所謂的 K2 先驗,它只是將“1”添加到每個單獨狀態的計數中。一個更明智的先驗選擇是 BDeu(貝葉斯狄利克雷等效均勻先驗)。
我繼續使用灑水器數據集來學習其參數,并檢測條件概率表(CPTs)。 要學習參數,我們需要一個有向無環圖(DAG)和一個具有完全相同變量的數據集。 思路是將數據集與 DAG 連接起來。在之前的示例中,我們已經計算出了 DAG(圖 3)。
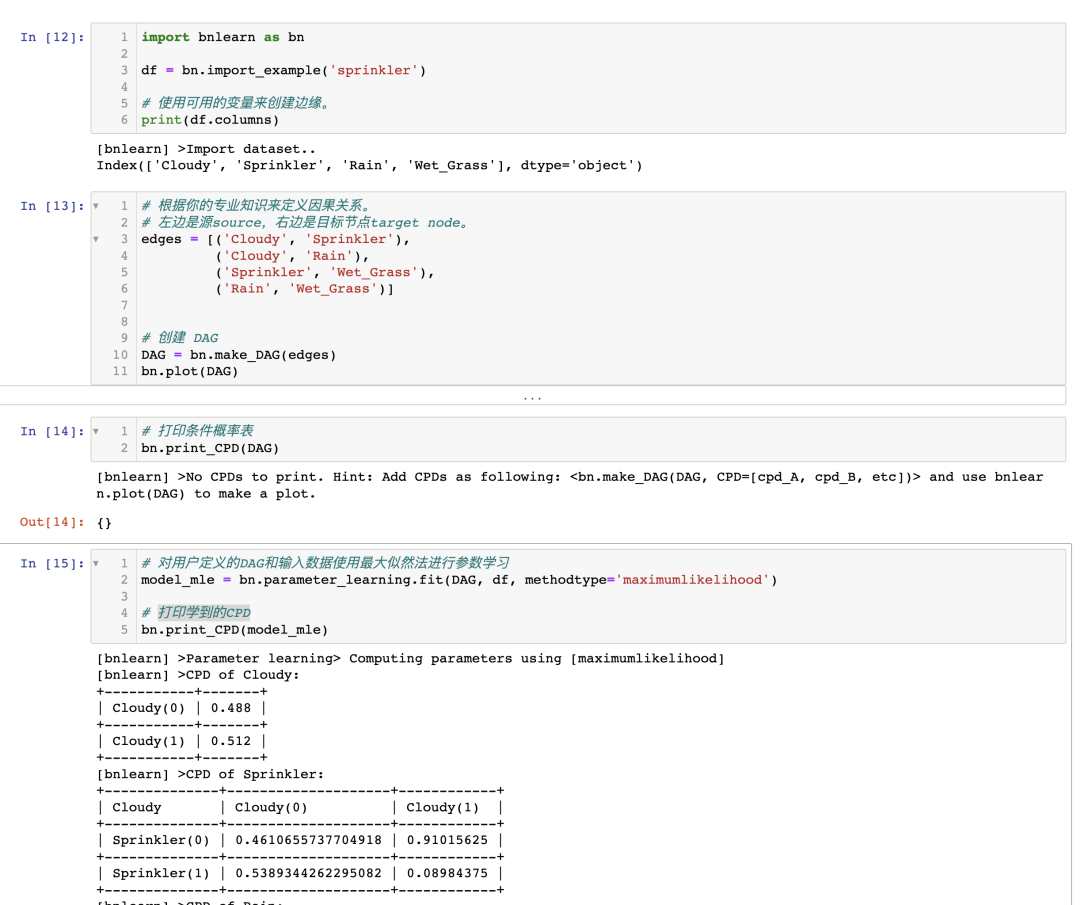
如果你已經到達這一點,您已經使用最大似然估計(MLE)基于 DAG 和輸入數據集 df 計算了 CPTs(圖 4)。請注意,為了清晰起見,CPTs 在圖 4 中包含在內。
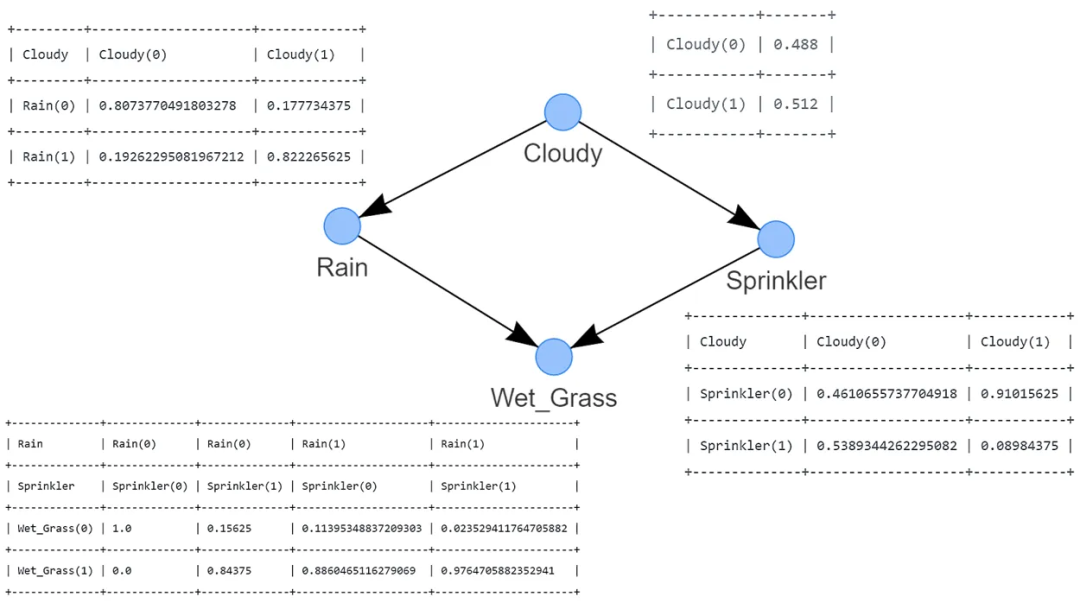
圖 4:使用最大似然估計進行參數學習推導的 CPTs 使用 MLE 計算 CPTs 非常簡單,讓我通過示例來演示一下,手動計算節點 Cloudy 和 Rain 的 CPTs。
# Examples to illustrate how to manually compute MLE for the node Cloudy and Rain:# Compute CPT for the Cloudy Node:# This node has no conditional dependencies and can easily be computed as following:# P(Cloudy=0)sum(df['Cloudy']==0) / df.shape[0] # 0.488# P(Cloudy=1)sum(df['Cloudy']==1) / df.shape[0] # 0.512# Compute CPT for the Rain Node:# This node has a conditional dependency from Cloudy and can be computed as following:# P(Rain=0 | Cloudy=0)sum( (df['Cloudy']==0) & (df['Rain']==0) ) / sum(df['Cloudy']==0) # 394/488 = 0.807377049# P(Rain=1 | Cloudy=0)sum( (df['Cloudy']==0) & (df['Rain']==1) ) / sum(df['Cloudy']==0) # 94/488 = 0.192622950# P(Rain=0 | Cloudy=1)sum( (df['Cloudy']==1) & (df['Rain']==0) ) / sum(df['Cloudy']==1) # 91/512 = 0.177734375# P(Rain=1 | Cloudy=1)sum( (df['Cloudy']==1) & (df['Rain']==1) ) / sum(df['Cloudy']==1) # 421/512 = 0.822265625請注意,條件依賴關系可能基于有限的數據點。例如,基于 91 個觀測結果。如果 Rain 有更多的狀態和/或更多的依賴關系,這個數字可能會更低。更多的數據是否是解決方案?也許是,也許不是。只要記住,即使總樣本量非常大,由于狀態計數是針對每個父節點的配置進行條件計數,這也可能導致分段。與 MLE 方法相比,查看 CPT 與之間的差異。

4.2.2. 在 Sprinkler 數據集上進行推理
進行推理需要貝葉斯網絡具備兩個主要組成部分:描述數據結構的有向無環圖(DAG)和描述每個節點與其父節點之間的統計關系的條件概率表(CPT)。到目前為止,您已經擁有數據集,使用結構學習計算了 DAG,并使用參數學習估計了 CPT。現在可以進行推理了! 在推理中,我們使用一種稱為變量消除的過程來邊緣化變量。變量消除是一種精確的推理算法。通過簡單地將求和替換為最大函數,它還可以用于確定具有最大概率的網絡狀態。不足之處是,對于大型的貝葉斯網絡,它可能在計算上是棘手的。在這些情況下,可以使用基于采樣的近似推理算法,如 Gibbs 采樣或拒絕采樣 [7]。 使用 bnlearn,我們可以進行如下的推理:
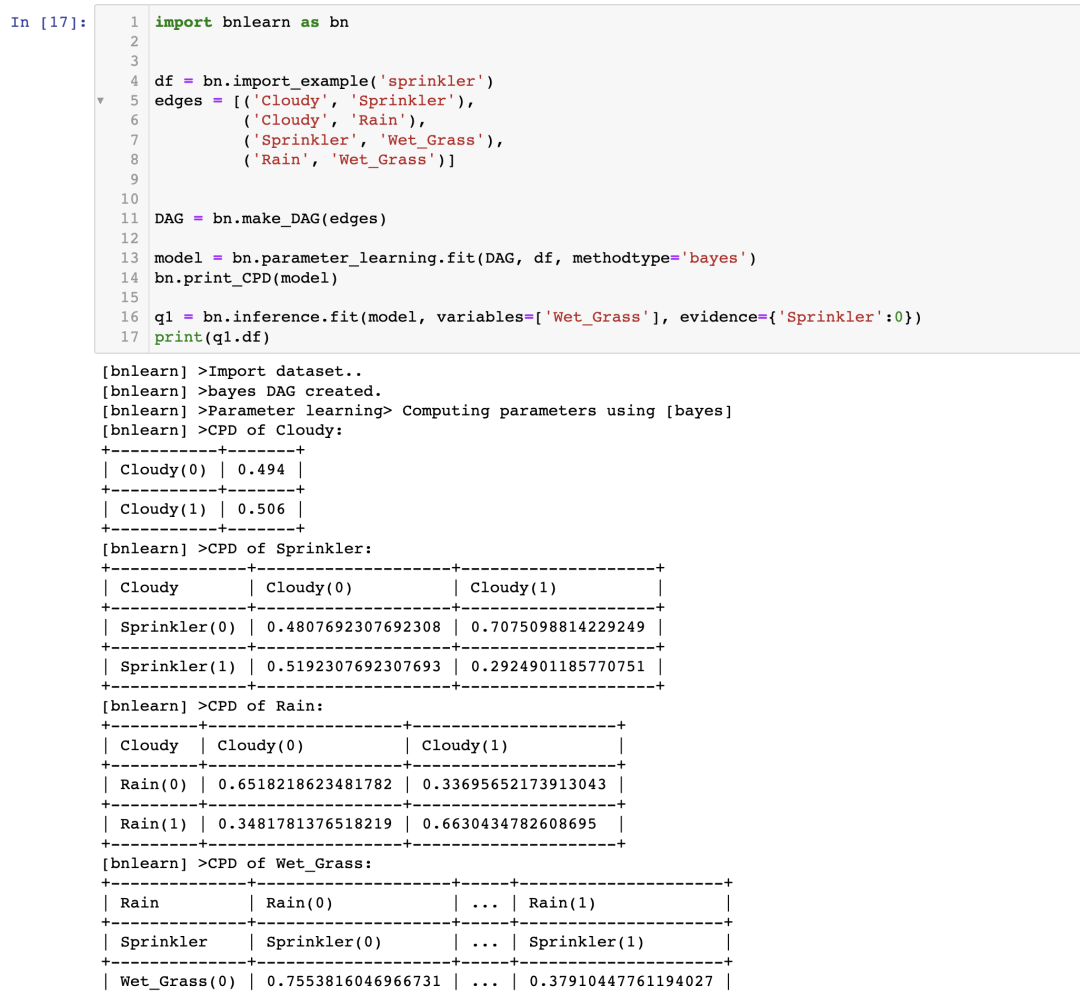

現在我們已經得到了我們的問題的答案:
如果噴灌系統關閉,草坪潮濕的可能性有多大?P(Wet_grass=1 | Sprinkler=0) = 0.51 如果噴灌系統關閉并且天陰,有下雨的可能性有多大?P(Rain=1 | Sprinkler=0, Cloudy=1) = 0.663
4.3. 我如何知道我的因果模型是正確的?
如果僅使用數據來計算因果圖,很難完全驗證因果圖的有效性和完整性。然而,有一些解決方案可以幫助增加對因果圖的信任。例如,可以對變量集之間的某些條件獨立性或依賴性關系進行經驗性測試。如果它們在數據中不存在,則表明因果模型的正確性 。或者,可以添加先前的專家知識,例如 DAG 或 CPT,以在進行推理時增加對模型的信任。
5. 討論
在本文中,涉及了一些關于為什么相關性或關聯不等于因果性以及如何從數據向因果模型的轉變使用結構學習的概念。 貝葉斯技術的優勢總結如下:
后驗概率分布的結果或圖形使用戶能夠對模型預測做出判斷,而不僅僅是獲得單個值作為結果。
可以將領域/專家知識納入到 DAG 中,并在不完整信息和缺失數據的情況下進行推理。這是可能的,因為貝葉斯定理基于用證據更新先驗項。
具有模塊化的概念。
通過組合較簡單的部分來構建復雜系統。
圖論提供了直觀的高度交互的變量集。
概率論提供了將這些部分組合在一起的方法。
然而,貝葉斯網絡的一個弱點是尋找最佳 DAG 在計算上很耗時,因為必須對所有可能的結構進行詳盡搜索。 窮舉搜索的節點限制可以達到約 15 個節點,但也取決于狀態的數量。如果有更多的節點,就需要使用具有評分函數和搜索算法的替代方法。盡管如此,要處理具有數百甚至數千個變量的問題,需要使用基于樹或基于約束的方法,并使用變量的黑名單/白名單。這種方法首先確定順序,然后找到該順序的最佳 BN 結構。這意味著在可能的排序搜索空間上進行工作,這比網絡結構空間小得多。 確定因果關系可能是一項具有挑戰性的任務,但 bnlearn 庫旨在解決其中一些挑戰,如結構學習、參數學習和推理。它還可以推導出(整個)圖的拓撲排序或比較兩個圖。
-
模型
+關注
關注
1文章
3172瀏覽量
48711 -
貝葉斯網絡
+關注
關注
0文章
24瀏覽量
8290 -
機器學習
+關注
關注
66文章
8377瀏覽量
132407
原文標題:貝葉斯網絡的因果關系檢測(Python)
文章出處:【微信號:DBDevs,微信公眾號:數據分析與開發】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 貝葉斯網絡的因果關系檢測(Python)
貝葉斯網絡的因果關系檢測(Python)










評論