大學課程中應該嚇倒了很多人,談傅里葉色變了。
本次就來重新認識一下電子硬件中的傅里葉變化。
首先理解之前,當然是需要先知道傅里葉這位大牛的人物百科啦。
傅里葉是法國數學家,物理學家。曾推導出著名的熱傳導方程,并在求解的過程中發現了解函數可以由三角函數構成的級數形式表示。
從而提出了任一函數都可以變成三角函數的無窮級數。傅里葉變換等理論也是由此創始。
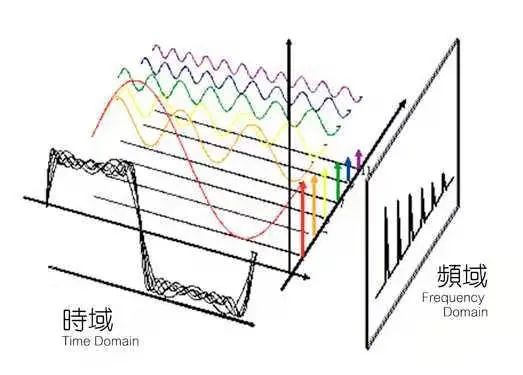
傅里葉變換的核心是從時域到頻域的變換。理解這句話就理解了傅里葉變換。
將它拆分開來進行理解
時域是什么?
時域是描述一個數學函數或者物理信號與時間的關系,比如說位移與時間的關系(速度),做的總功與時間的關系(功率)等等。
很多物理量的定義都與時間有關,所以對于時域的理解會更加直觀。
頻域是什么?
頻域就是描述頻率所用到的空間或者說坐標系。比如說坐標系,通常橫軸是頻率,縱軸是該頻率的幅度。

比如說一個波,頻率就是它每秒鐘波形重復的次數,某個頻率下的振幅就是它頻率的幅度。
最難理解的就是頻域轉時域,或時域轉頻域的轉換關系了?他們是如何轉換的?
頻域是把時域波形通過傅里葉變換或者拉普拉斯變化,得到頻域的表達式,所以可以得到頻譜圖,它是描述頻率變換和幅度變化的關系。



比如說一個人的聲音,從時域方面主要是兩個參考因素,就是時間和振幅。如果要將聲音放大,只需要使用放大器放大振幅即可。
但是要怎么將聲音實現低音呢?
這就有點抽象復雜了,就如同家庭影音中的低音炮,它是怎么實現重低音的?
事實上,所謂的實現低音,就是將聲音中的低音部分進行保留或者增強,突出低音的表現。
所以就需要用到低通濾波器(LPF,傳遞低頻信號,衰減高頻信號的濾波器),將低音部分的頻率單獨過濾出來,對這部分頻率的波形通過時域頻域轉換,調整低音部分的振幅,從而實現“低音”的效果。
-
函數
+關注
關注
3文章
4237瀏覽量
61971 -
時域
+關注
關注
1文章
68瀏覽量
28466 -
傅里葉變換
+關注
關注
6文章
426瀏覽量
42483 -
頻譜圖
+關注
關注
0文章
4瀏覽量
5909
發布評論請先 登錄
相關推薦
小波與傅里葉分析基礎





 電子硬件中的傅里葉變化
電子硬件中的傅里葉變化










評論