歡迎來到森木磊石「技術微課堂」,本期為大家分享經典控制算法之一的PID控制方法。
PID控制方法從提出至今已有百余年歷史,其由于結構簡單、易于實現、魯棒性好、可靠性高等特點,在機電、冶金、機械、化工等行業中應用廣泛。
下面就跟著小編一起來學習PID算法的原理分析及優化,快來get!
一、PID原理
PID控制方法將偏差的比例(proportional)、積分(integral)、微分(derivative)通過線性組合構成控制量,對被控對象進行控制。
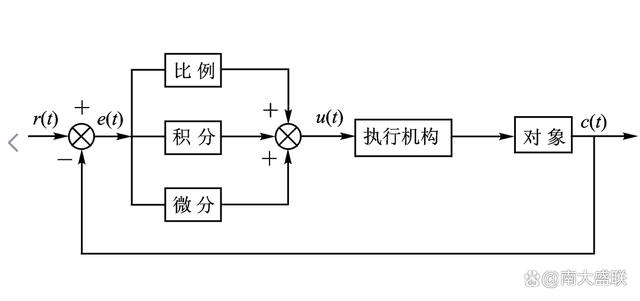
常規的PID控制系統如圖所示:
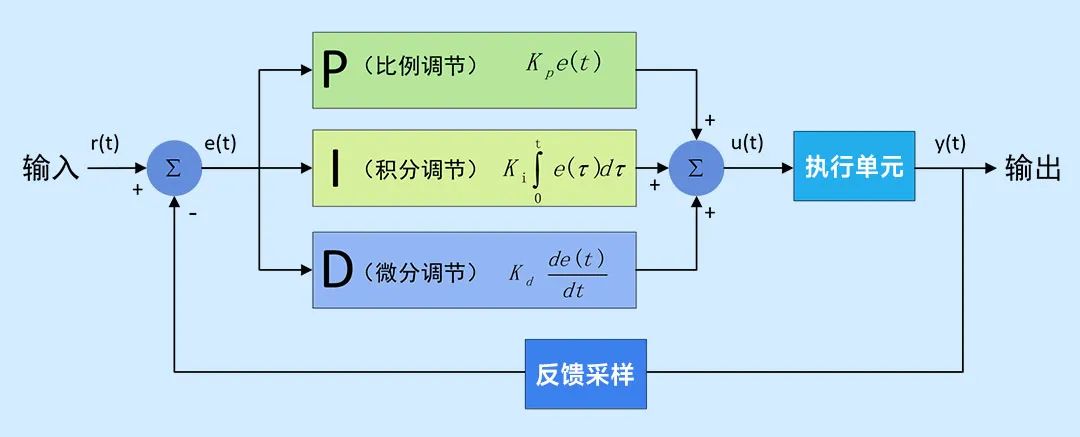
系統的輸入r(t)為控制量的目標輸出值,輸出y(t)為控制量的實際輸出值,e(t)為輸出量目標值與實際值的偏差量,PID算法的調控是基于e(t)進行的。
比例調節是基于實際值與目標值的偏差量進行線性調節,在系統中表現為Kpe(t),Kp為比例增益。
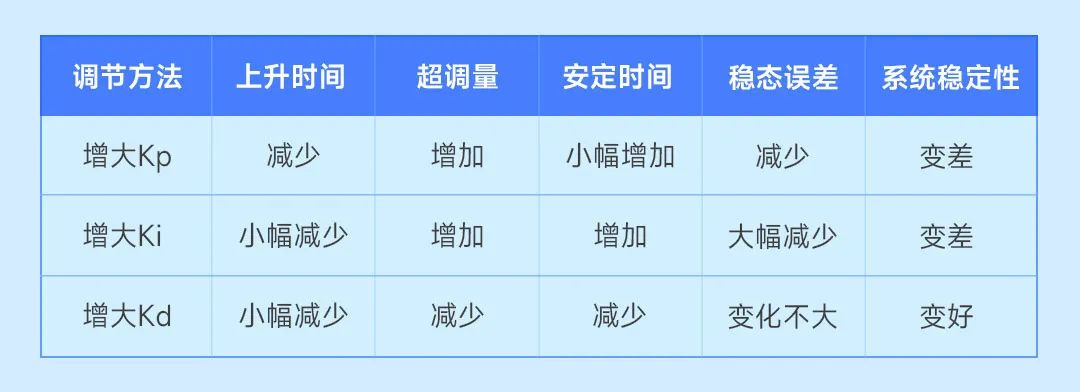
比例增益Kp越大調節作用越激進,輸入輸出的微小偏差都會造成很大的調節動作;相反的Kp越小調節作用越保守,即使輸入輸出差異很大系統的調節效果都不太明顯。
積分調節是利用歷史偏差量的累計對系統輸出進行調節,在系統種表示為:
t
Ki∫ e(t)dt,Ki為積分增益。
0
積分調節的意義是消除系統的穩態誤差。積分增益Ki越大系統的穩態誤差消除的越快,Ki越小系統的穩態誤差越不易消除,系統的調節精度越差。但是Ki過大會在響應過程產生較大超調,導致積分飽和現象的產生。
微分調節是基于偏差量的變化速率(偏差求導)對系統輸出進行調節,在系統種表示為:
de(t)
Kd ———— ,Kd為微分增益。
dt
微分調節主要起到阻尼的作用,抑制超調。微分增益Kd越大,系統的穩定性越好,調節過程中曲線波動越小。但是Kd若設置過大會使得系統的調節時間增長,抗干擾性減弱。
偏差值在經過三種調節作用后會產生一個控制量u(t),u(t)將通過執行單元控制輸出。系統將利用采樣單元將輸出反饋給輸入端進行偏差量計算。
常規PID控制系統中u(t)與e(t)之間的函數關系如下:
t de(t)
u(t)=Kpe(t)+Ki∫ e(t)dt+Kd ———— 式1
0 dt
分別調節Kp、Ki、Kd參數對PID控制系統性能的影響如下表所示:
二、數字PID控制
隨著計算機技術發展,目前多以微控制器或計算機為運算核心,利用軟件程序來實現PID控制和校正,也就是數字PID控制。常用的數字PID控制方法有:位置式PID、增量式PID以及步進式PID等。
01位置式PID
由于計算機的運算是離散的,要想實現數字PID控制首先需要將連續函數進行離散化。
我們用誤差的累加替代積分運算,用誤差的差分代替微分運算,可得:
k
u(k)=Kpe(k)+ki ∑ e(j)+kd(e(k)-e(k-1)) 式2
j=0
其中k為采樣序列號(k=0,1,2,3......),e(k)為第k次采樣時的誤差值,e(k-1)為第k-1次采樣時的誤差值u(k)為第k次采樣時控制量的輸出值。在位置式PID中輸出u(k)直接控制待控制對象,u(k)的值和控制對象是一一對應的關系。
從式2可以看出,位置式PID需要計算第k次和k-1次的誤差,控制器會對偏差進行累加,這樣會使得系統的運算量變大,占用內存過多,給計算機帶來負擔。
同時,控制器的每次輸出u(k)都和過去的狀態有關,u(k)的大幅變化會導致執行機構的狀態大幅變化,系統抗干擾能力差。
為了改善這些問題,有學者提出了數字PID的另外一種實現方法——增量式PID。
02增量式PID
增量式PID的輸出是對被控對象的增量?u(k),而不是實際的控制量大小。
?u(k)=u(k)-u(k-1)
=kp(e(k)-e(k-1))+kie(k)+kd(e(k)-2e(k-1)+e(k-2))
=a0e(k)+a?e(k-1)+a?e(k-2)
其中a0=kp+ki+kd,a?=-Kp-2kd,a?=kd。
從上式可以看出增量式PID跟k時刻、k-1時刻、k-2時刻的偏差都有關系,但是不會對偏差進行累積,所以相比位置式PID的計算量要小,也不會跟過去的偏差有關聯,所以控制系統的穩定性好。
03步進式PID
當PID系統的設定值發生較大的突變時,系統很容易產生超調,影響其穩定性。為了避免階躍信號帶來的不利影響,有學者提出了步進式PID。
步進式PID不對階躍信號進行直接響應,而是按照設定的步進規則逐漸增加設定值,使得信號逐步靠近目標值,這樣被控對象運行平穩,避免了因突變帶來的超調。
這種方法并未改變PID算法結構本身,而是對設定值進行步進處理,使其不產生突變。步進處理方法有很多種,最為常見的是建立一個線性變化函數,確定變化步長,當檢測到目標值發生變化后按照步長逐步調整設定值。
Ys=Yn+kT
其中Ys為設定目標值,Yn為當前目標值,T為步長,k為變化系數。當檢測到目標值增加時k=1,當目標值不變時k=0,當目標值減小時k=-1。
步進式PID雖然可以減少階躍信號帶來的干擾,但是也會讓系統的響應速度變慢,可以調節步長來平衡兩者之間的關系。步長越小運行越穩定,系統響應速度越慢,反之亦然。
三、PID算法優化
01積分飽和優化處理
若系統持續存在一個方向的偏差時,PID控制器的輸出由于積分作用不斷累加而增大,從而導致控制器輸出產生超調進入飽和區。
當系統出現反向偏差時,由于輸出飽和而不能對反向的偏差進行快速響應,這種現象稱為積分飽和。

常用抑制PID積分飽和方法有:積分分離法、遇限削弱積分法以及變速積分法等。
//積分分離法
當系統檢測到偏差e(k)較大時,取消積分環節,當被控量接近給定值時,誤差減小,此時恢復積分環節。這樣既不影響控制器的動態性能,又能避免出現嚴重超調或持續振蕩現象。
//變速積分法
根據系統的偏差e(k)大小對積分速度進行調整,當e(k)絕對值很大時減慢積分速度,當e(k)絕對值很小時加快積分速度。在積分飽和時減小積分時間可以達到抑制積分飽和的效果,增強系統的適應性。
//遇限削弱積分法:
當檢測到控制量u(k)進入飽和區時不再進行積分項累加,而執行削弱積分的運算。這樣不會產生過多的超調量,當需要反向調節時能較快地響應,避免輸出長時間停留在飽和區。
02微分項優化處理
PID算法中微分項與偏差的變化速率有關。如果系統存在頻率較高的干擾或突變等情況時,微分項的數值會不斷跳變,使控制過程產生系統振蕩,影響控制系統的穩定性。

常用的微分環節優化方法如下:
//微分先行:
微分項對測量值產生的偏差起作用,而不是對設定值起作用。這樣可以避免設定值的變化而產生較大的調節波動,抑制高頻干擾引起的系統振蕩。
//不完全微分:
不完全微分是在微分作用后引入一階慣性環節,使得在偏差作階躍式變化時產生的微分調節量,以一種較為平緩的方式輸出。這樣在不減小微分調節作用的前提下,降低因為偏差突變產生的波動。
//受控微分法:
受控量微分PID算法是對控制器的輸出值進行微分,而不是對系統響應的實際輸出值進行微分,可避免由于系統設定值頻繁變化或執行器的振蕩產生的系統響應超調量過大。
03串級PID
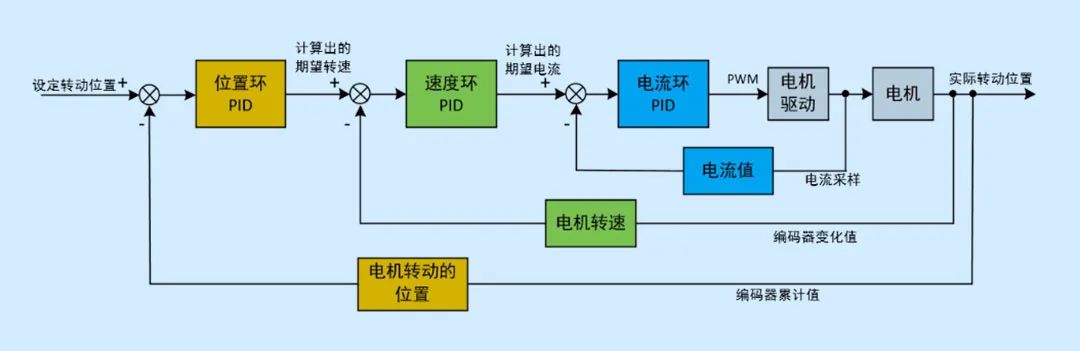
所謂串級PID,就是采用多個PID控制器串聯工作,外環控制器的輸出作為內環控制器的設定值,由內環控制器的輸出去操縱外環控制器,從而實現外環被控量的控制效果。串級PID能夠有效改善控制質量,在過程控制中應用廣泛。
控制系統以外環控制器為主導,保證外環主變量穩定為目的,兩個控制器協調一致,互相配合。外環控制器按負荷和操作條件的變化不斷糾正內環控制器的設定值,使內環控制器的設定值適應負荷和操作條件的變化。
在電機控制中串級PID十分常見,常用的位置環+速度環+電流環控制結構如圖。
在PID控制方法中P、I、D是三種不同的調節作用,在實際應用時可根據需求對三種調節作用進行靈活組合,這也是PID控制方法的魅力所在,它的結構決定了它在實際應用中的多樣性與靈活性。
本篇主要從PID原理、數字PID實現方式以及算法優化方面進行了簡單介紹,希望能夠對大家學習PID算法有所幫助。
-
控制
+關注
關注
4文章
1005瀏覽量
122506 -
PID
+關注
關注
35文章
1466瀏覽量
84830
發布評論請先 登錄
相關推薦
第13章-循跡功能 STM32智能小車循跡教程 PID循跡算法分析

什么是PID?PID各個參數有什么作用?
STM32控制中常見的PID算法總結
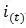
四軸PID算法:單環和串級,你搞懂了嗎?
PID算法的代碼實現
飛行控制PID算法的作用解析
單片機如何實現pid控制 基于pid控制的STM32代碼實現
PID算法詳解及實例分析
控制算法PID之比例控制(P)的原理和示例代碼





 PID算法原理分析及優化
PID算法原理分析及優化










評論