比起理解紅黑樹的原理,更重要的是理解紅黑樹的應用場景,因為某些應用場景的需要,紅黑樹才會應運而生。
紅黑樹的特點:
插入,刪除,查找都是O(logn)的復雜度。
紅黑樹的應用:
- epoll的實現,內核會在內存開辟一個空間存放epoll的紅黑樹,并將每個epollfd加入到紅黑樹中,一般epoll會設置LT水平觸發,當網卡有數據到來,可讀緩沖區不為空,會觸發回調EPOLLIN事件,而之前注冊了對EPOLLIN事件感興趣的socketfd會有專門的隊列存儲,內核會遍歷隊列搜尋對應的socketfd,因為在紅黑樹里找有近似O(logn)的時間復雜度,所以10億個socket也只需要20次查找。
- 進程調度,內核CFS隊列,以紅黑樹的形式存儲進程信息。
- 有的hashtable(記得是java),當沖突時不以鏈表來組織重復元素,而是以紅黑樹的形式來組織。
- 內存管理,比如空閑鏈表freelist可以通過紅黑樹來組織,這樣malloc的時候要找到符合大小的內存塊,如果不是firstfit的原則,而是全局最優大小原則,想找到適合的內存塊就可以通過紅黑樹來找。
- Nginx的Timer事件管理。
紅黑樹定義
寫代碼之前先寫一下紅黑樹的規則吧
- 每個顏色不是紅就是黑。
- 根節點必黑
- 葉子節點必黑
- 紅色節點的左右孩子都為黑
- 每個節點到其葉子節點(nil)的所有路徑上的黑色節點數量都一樣
我的理解:從任一節點到葉子結點的路徑上,路徑的元素必然有黑色節點,而路徑的長度則取決于路徑上紅色節點的數量,最短的路徑上,所有節點都是黑色,這種情況下,查找效率為真實的O(logn),和嚴格平衡的AVL樹一致。而如果在剛剛的最短路徑上,也就是所有黑色節點的中間插入紅色節點,這樣是不會打破紅黑樹的平衡的(規則5),此時便是最長路徑,查找效率為2logn,但依然和logn在同一數量級,因此,紅黑樹的查找效率可以看做是(Ologn),同時比AVL樹擁有更高的插入和刪除效率。
紅黑樹代碼框架
using Color = bool;//-顏色因為只有紅或者黑,選擇bool類型
using KEY_TYPE = int;//-為了更好理解紅黑樹,就不寫成模板類了,所以首選萬年int(笑~)
using VALUE_TYPE = int;//-同理
//-全局靜態紅黑變量
static const Color red = false;
static const Color black = true;
//-紅黑樹的節點特點,有color,有parent
class RBtree_node{
public:
Color color;
RBtree_node * parent;
RBtree_node * left;
RBtree_node * right;
KEY_TYPE key;//-后期如果想解耦合,可以將key和value抽離出去
VALUE_TYPE value;
RBtree_node(Color color_):color(color_),parent(nullptr),left(nullptr),right(nullptr),key(-99999){}
RBtree_node(Color color_, KEY_TYPE key_,RBtree_node * nil):
color(color_),parent(nil),left(nil),right(nil),key(key_){}
};
class RBtree{
private:
//-紅黑樹數據成員:其中nil的意義在于,因為紅黑樹的所有葉子節點都是黑色的,所以可以將所有臨近末尾的節點,
//-都連接到這一個葉子結點nil上,同理,root的parent也可以連接到nil上,形成一個dummy空節點
RBtree_node * root;
RBtree_node * nil;
public :
//-以下實現了紅黑樹常用接口:
//-構造函數
RBtree(){
nil = new RBtree_node(black);//-為所有葉子節點nil初始化,顏色為黑色
root = nil;//-紅黑樹為空的時候,讓nil作為root
}
//-左旋
void leftRotate(RBtree_node *left_node);
//- 右旋
void rightRotate(RBtree_node * right_node);
//-插入key
void insertNode(KEY_TYPE key);
//-修復插入
void fixInsert(RBtree_node * node);
//-查找某個key的節點
RBtree_node* searchNode(KEY_TYPE key);
//-查找某個節點的中序后繼
RBtree_node* successor(RBtree_node * node);
//-刪除key
void deleteNode(KEY_TYPE key);
//-修復刪除
void fixDelete(RBtree_node * node);
//-層序遍歷打印紅黑樹
void print();
//-打印中序遍歷
void printMiddle(RBtree_node * node);
};
接下來將接口一一實現:
紅黑樹節點左旋右旋:
實現參照該圖,至于學習方法也沒啥捷徑,只能把這個結構圖和變換方式深深印刻在腦海里。
手撕代碼的時候想象一下還是容易寫的,如果覺得這樣很累就紙上畫個草圖。
由于左旋和右旋是對稱的,所以規則只需要記一半。
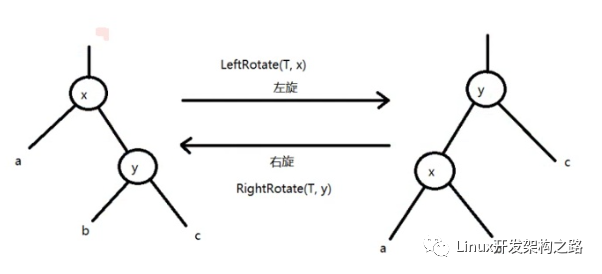
圖1 左旋右旋
//-左旋
void RBtree::leftRotate(RBtree_node *left_node){
RBtree_node * right_node = left_node->right;//-右節點的左枝條接在左節點的右枝條上
left_node->right = right_node->left;
if(right_node->left!=nil){
left_node->right->parent = left_node;
}
//-右節點接在左節點的父親上
right_node->parent = left_node->parent;
if(left_node == root){
//-nil不會指向任何節點,但是root->parent是nil
root = right_node;
}
else if(left_node == left_node->parent->left){
left_node->parent->left = right_node;
}else{
left_node->parent->right = right_node;
}
//-左節點接在右節點的左枝上
left_node->parent = right_node;
right_node->left = left_node;
}
//- 右旋:寫完左旋后,把所有left和right對調即可
void RBtree::rightRotate(RBtree_node * right_node){
RBtree_node * left_node = right_node->left;
right_node->left = left_node->right;
if(left_node->right!=nil){
right_node->left->parent = right_node;
}
left_node->parent = right_node->parent;
if(right_node == root){
root = left_node;
}
else if(right_node == right_node->parent->right){
right_node->parent->right = left_node;
}else{
right_node->parent->left = left_node;
}
right_node->parent = left_node;
left_node->right = right_node;
}
紅黑樹的插入,插入修復
插入的步驟原理:
- 找到插入位置,注意紅黑樹新節點的插入位置都是葉子結點。
- 如果紅黑樹中沒有節點,插入節點需要改變root指向,同時將root的parent指向nil。
- 改變插入節點父親的左右指針,同時插入節點本身的左右指針指向nil。
- 如果插入節點的父親是紅色,說明平衡被打破了,需要執行修復插入,讓紅黑樹恢復平衡
要點:
- 如果在查找的時候發現元素已經存在,我這里就直接拋棄了新元素的插入,如果要實現紅黑樹multimap的insert_equal功能可以自己實現一下。
- 為什么要插入修復?
首先我們會強制默認所有的新節點都是紅色節點。
因為紅色節點不論插在哪個位置,都不會破壞規則5(路徑上黑色節點數量相同),唯一可能破壞的是規則4(紅色節點的孩子必黑),由于破壞規則5比破壞規則4要容易得多,所以將新節點設置為紅色可以盡量地避免破壞規則。
當新的紅色節點插入到一個紅色節點之后,破壞了規則4,才需要修復,如圖2,插入元素16
修復的意義和規則在于,如何將新紅節點的父親(34)變成黑色后,依然能保持紅黑樹的左右平衡,這個時候才涉及到對伯父節點(184)的討論
插入修復的步驟原理:
- 我們的目的是為了讓左邊cur為紅的情況下,使父親變黑且不會破壞平衡。
- 所以只要cur的parent是紅色,就一直循環。
- 判斷伯父節點(184),如果伯父節點是紅色,如圖2,那么同時將父親和伯父改成黑色就不會改變平衡,將祖父(101)變紅,讓cur變成祖父(101)進入下一輪迭代。

圖2 伯父(184)為紅
如果伯父節點是黑色,如圖3,插入節點16

圖3 伯父(184)為黑
那么將父親(34)變黑就會讓左邊多一個黑色,不過可以通過讓祖父(101)變紅,旋轉祖父,讓祖父下沉,父親上浮,這樣相當于讓老爹變黑同時左右都加了一個黑色,不會破壞平衡。
- 但是旋轉祖父需要有個前提條件,插入節點不能是父親的靠內節點,如圖4,插入節點(36)為右孩子,父親(34)是祖父(101)左枝。
圖4,插入節點(36)是靠內節點
一旦右旋祖父(101),就會破壞cur(36)和父親(34)的連接關系,所以必須要把cur從靠內節點變成靠外節,一個方便的方式是讓父親成為新cur(34),并右旋cur(34),如圖5,之后再進行上個步驟,將新父親(36)變黑,祖父(101)變紅,右旋祖父。

圖5 原cur(36)經過旋轉變為父親,將34作為新cur
要點:
- 終止條件,當當前節點(紅)的父親為黑的時候打破循環(注意回溯到nil的時候的,nil也是黑色)
- 終止循環后,注意如果回溯到root,會改變root的顏色為紅,需要在循環結束后fix成黑色。
- 因為父親是祖父左枝也好右枝也好,變換總是左右對稱的,所以規則只需要記一半。
void RBtree::insertNode(KEY_TYPE key){
RBtree_node * prev = nil;
RBtree_node * cur = root;
while(cur!=nil){
prev = cur;
if(key>cur->key){
cur = cur->right;
}else if(keykey){
cur = cur->left;
}else{//-該key已經存在
return;
}
}
//-創建新節點
RBtree_node * new_node = new RBtree_node(red,key,nil);
//-如果節點沒有元素
new_node->parent = prev;
if(prev == nil){
root = new_node;
}
else if(key key){
prev ->left = new_node;
}else{
prev ->right = new_node;
}
fixInsert(new_node);
print();
}
//-修復插入
void RBtree::fixInsert(RBtree_node * new_node){
while(new_node -> parent->color == red){//-終止條件要注意
//-如果父親是左枝
if(new_node->parent == new_node -> parent->parent->left){
//-獲得其伯父節點
RBtree_node * uncle = new_node->parent->parent->right;
if(uncle->color == red){//-如果伯父是紅色,那么將父親和伯父同時變黑,不會破壞左右平衡
uncle->color = black;
new_node->parent->color = black;
new_node->parent ->parent->color = red;//-將祖父變紅,才能實現下一輪回溯修復
new_node = new_node->parent->parent;
}else{//-如果伯父是黑色
//-判斷new_node是不是右孩子,如果是右孩子轉換成左孩子
if(new_node == new_node -> parent->right){
new_node = new_node->parent;
leftRotate(new_node);
}
//-此時紅色節點是左孩子
//-如果結構本是平衡狀態,右邊本該比左邊多一個黑,但是我們將父親(左)變黑會破壞平衡,
//-所以需要右旋祖父,把父親上浮,相當于在左枝多一個黑的時候給右枝也多了黑,這樣左右就能平衡
new_node->parent->color = black;
new_node->parent ->parent->color = red;
rightRotate(new_node->parent->parent);
}
}
//-如果父親是右枝(將上邊代碼的left和right全部對調即可,不用記規則)
else {
RBtree_node * uncle = new_node->parent->parent->left;
if(uncle->color == red){//-如果伯父是紅色
uncle->color = black;
new_node->parent->color = black;
new_node->parent ->parent->color = red;
new_node = new_node->parent->parent;
}else{//-如果伯父是黑色
if(new_node == new_node -> parent->left){
new_node = new_node->parent;
rightRotate(new_node);
}
new_node->parent->color = black;
new_node->parent ->parent->color = red;
leftRotate(new_node->parent->parent);
}
}
}
//-如果new_node回溯到root,此時root->parent==nil(black)打破了循環,而此時root被改變成了黑色,違反了規則1,
//-所以最后需要強行把root fix成黑色
root->color = black;
}
紅黑樹查找某個key,以及找到某個節點的中序后繼
主要講下怎么根據當前節點找中序后繼,根據BST的特性
- 如果當前節點有右孩子:其后繼肯定在右枝條上,且是右枝條最左邊的元素。
- 如果當前節點沒有右孩子:根據中序遍歷的遞歸順序,假設cur是其父親的左孩子,cur遍歷完后,下一個節點(后繼)就是父親,反之,如果cur是右孩子,說明其父親也遞歸完了,需要回溯父親的父親,所以只需要一直往上找直到cur為其parent的左孩子為止,然后返回parent,而回溯到root的時候,root的父親雖然是nil,但是nil是沒有左右孩子的,所以退出循環。
RBtree_node* RBtree::searchNode(KEY_TYPE key){
RBtree_node * cur = root;
while(cur!=nil){
if(key>cur -> key){
cur = cur->right;
}else if(key < cur -> key){
cur = cur->left;
}else{
return cur;
}
}
return cur;
}
//-查找某個節點的中序后繼
RBtree_node* RBtree::successor(RBtree_node * node){
//-如果節點有右孩子
if(node->right!=nil){
RBtree_node * res = node -> right;
while(res->left!=nil){
res = res->left;
}
return res;
}else{
while(node!=root&&node!=node->parent->left){
node = node->parent;
}
return node->parent;
}
}
紅黑樹刪除,修復刪除
刪除的步驟原理:
- 類似二叉堆,當我們從棧頂pop元素后,需要用二叉樹末尾節點代替原來的root,而后從二叉堆頂部開始向下修復,同理,我們要刪除樹上的一個節點,自然需要一個節點來頂替刪除節點(key_node)的位置,因次,我們并不一定要在數據結構上真正刪除key_node,可以找到那個頂替節點(delete_node),將頂替節點的數據覆蓋key_node,而在數據結構上真正刪除的是那個頂替節點(delete_node)。
- 在數據結構上真正刪除哪個節點(delete_node怎么取),取決于(key_node)是否有左右枝條,
- 如果key_node左右孩子都沒有,說明是葉子節點,直接刪除key_node即可,delete_node就是key_node本身。
- 如果key_node左右孩子只有其一,那么刪除key_node只需要將孩子接在祖父上,刪除自己即可,所以delete_node依舊是key_node本身。
- 如果key_node左右孩子都有,那么可以根據上面的successor函數,找到key_node的直接后繼,也就是刪除節點右邊最小的元素,將其本身數據用來頂替key_node,不會破壞BST的性質。之后將其作為delete_node在數據結構上刪除即可,如圖6。
圖6
找到delete_node后,還要找到delete_node的孩子(delete_son),將delete_son接在delete_node的父親上。
- 判斷delete_node是否是黑色,如果是黑色,則刪除了該元素必會破壞紅黑樹的平衡(規則5),需要修復fix_delete,而修復從delete_son開始。
要點:
- 記得額外判斷如果delete_node是root的情況,需要更新其孩子delete_son為新的root。
修復刪除的步驟原理:
- 刪除節點delete_node如果是黑色的,說明樹中有一個枝條(假設是左枝)的黑色節點必會比兄弟枝條(右枝)少一個。我們怎么才能使左右重新平衡,要么讓左枝條黑色節點+1,要么讓右枝條黑色節點-1。后續步驟全都以delete_son為其父左枝條為例,因為對稱,依舊只需要記一半的規則。
- 讓delete_son的兄弟bro變成黑色,如果bro是紅色,則bro->黑色,parent->紅色,左旋parent,此時bro的左枝會變成新的bro,因為bro是紅色,所以根據規則4,左枝必為黑,即新bro變為黑色。
- 判斷bro的孩子,
- 如果左黑右黑,將bro->紅色,不會改變bro后續孩子的平衡,同時,bro所在的右枝條的黑色節點-1,紅黑樹重新平衡,將父親作為新的delete_son繼續循環,直到delete_son為紅色。
- 如果左紅右黑,通過右旋bro,變成左黑右紅。
- 如果左黑右紅。bro繼承父親的顏色,將bro的父親變黑,右孩子變黑(右枝黑+1),左旋父親(左枝黑+1,右枝黑-1),總的來說delete_son所在的左枝條的黑色節點+1,紅黑樹重新平衡,并且直接讓delete_son=root退出循環。
要點:
- 終止條件:當delete_son==root或者delete_son為紅的時候終止循環。
void RBtree::deleteNode(KEY_TYPE key){
//-查找key所在節點
RBtree_node * key_node = searchNode(key);
//-實際刪除的節點
RBtree_node* delete_node;
//-delete_node的孩子
RBtree_node* delete_son;
//-如果同時有左枝或者右枝條
if(key_node->left != nil&&key_node->right != nil){
delete_node = successor(key_node);
delete_son = delete_node->right;
}//-如果僅有左枝或者右枝條或者左右都沒有
else{
delete_node = key_node;
if(key_node->left != nil){
delete_son = key_node->left;
}else{
delete_son = key_node->right;
}
}
//-刪除deletenode
delete_son->parent = delete_node->parent;
//-先判斷deletenode是不是根節點
if(delete_node == root){
root = delete_son;
}
else if(delete_node == delete_node->parent->left){
delete_node->parent->left = delete_son;
}else{
delete_node -> parent -> right = delete_son;
}
//-覆蓋key_node原有數據
key_node->key = delete_node -> key;
key_node ->value = delete_node -> value;
//-如果刪除節點是黑色的,需要修復delete_son,注意是孩子
if(delete_node->color == black){
fixDelete(delete_son);
}
//-釋放空間
delete delete_node;
//-打印
print();
}
//-修復刪除
void RBtree::fixDelete(RBtree_node * delete_son){
//-修復的原因是因為delete_son所在的枝條的黑節點比另一個枝條少一個,所以不平衡,所以需要填上左邊缺失的黑,或者減掉右邊多余的黑
//-當delete_son是黑色的一直循環
while(delete_son!=root&&delete_son->color == black){
//-判斷delete_son所在枝條,如果是左枝
if(delete_son == delete_son->parent->left){
//-如果兄弟是紅色的
RBtree_node * bro = delete_son->parent->right;
if(bro->color == red){
bro->color = black;//-兄弟變黑
delete_son->parent->color = red;//-父親變紅
leftRotate(delete_son->parent);//-左旋父親,兄弟上浮,相當于左右都加了一個黑,不改變平衡狀態
bro = delete_son->parent->right;//-新的bro是原來bro的左枝,因為原bro是紅的,其左右枝都是黑色的,這樣保證新的兄弟是黑色的
}
//-此時兄弟是黑色的,判斷兄弟的孩子
//-左黑右黑(兄弟的孩子平衡了)
if(bro->left->color == black&&bro->right -> color == black){
bro->color = red;//-相當于右邊減去多的一個黑,達到平衡
delete_son = delete_son->parent;
}else{
//-如果是左紅右黑,變成左黑右紅
if (bro->right->color == black){
bro -> color = red;
bro->left->color = black;
rightRotate(bro);//-左節點上浮,相當于左右都加了一個黑,不改變平衡
}
bro->color = bro->parent -> color;
bro->parent -> color = black;
bro->right->color = black;//-給右邊加了一個黑
leftRotate(delete_son->parent);//-父親下沉,兄弟上浮,左邊加一個黑,右邊減一個黑,總體上左邊填上了缺少的黑也達到了平衡
delete_son = root;
}
}
//-如果是右枝(不用記規則,把上面的代碼left和right對調即可)
else {
RBtree_node * bro = delete_son->parent->left;
if(bro->color == red){
bro->color = black;
delete_son->parent->color = red;
rightRotate(delete_son->parent);
bro = delete_son->parent->left;
}
if(bro->right->color == black&&bro->left -> color == black){
bro->color = red;
delete_son = delete_son->parent;
}else{
if (bro->left->color == black){
bro -> color = red;
bro->right->color = black;
leftRotate(bro);
}
bro->color = bro->parent -> color;
bro->parent -> color = black;
bro->left->color = black;
rightRotate(delete_son->parent);
delete_son = root;
}
}
}
delete_son->color = black;
}
二叉樹層序遍歷和中序遍歷
每次插入刪除的時候,使用層序遍歷打印一遍二叉樹,可以驗證一下是否正確。
每個節點都有前綴,b代表黑節點,r代表紅節點。
void RBtree::print(){
std::deque dqueue;//-使用deque實現隊列
dqueue.push_back(root);
while(!dqueue.empty()){
int size = (int)dqueue.size();
for (int i = 0; i < size; ++i) {
RBtree_node* temp = dqueue.front();
dqueue.pop_front();
if(temp->left!=nullptr){
dqueue.push_back(temp -> left);
}
if(temp -> right != nullptr){
dqueue.push_back(temp -> right);
}
std::string color = temp->color?"b: ":"r: ";
std::string keystr = temp==nil?"nil":std::to_string(temp->key);
std::cout< }
std::cout< }
}
//-打印中序遍歷
void RBtree::printMiddle(RBtree_node * node){
if(node == nil){
return;
}
printMiddle(node->left);
std::string color = node->color?"b:":"r:";
std::cout
}<;
<*>
紅黑樹測試代碼
寫個循環來插入元素,輸入i插入元素,輸入d刪除元素,輸入q退出程序。
附上一個在線生成紅黑樹的連接,可以配合測試自己寫的紅黑樹的正確性
紅黑樹動畫在線演示
RBtree rb;
std::string select;
KEY_TYPE key;
while(true){
std::cout<<"n輸入操作:i:插入key,d:刪除key q:退出"< std::cin>>select;
if(select == "i"){
std::cout<<"輸入key"< std::cin>>key;
rb.insertNode(key);
}else if(select == "d"){
std::cout<<"輸入key"< std::cin>>key;
rb.deleteNode(key);
}else if(select == "q"){
break;
}else{
std::cout<<"輸入不合法,重新輸入"< }
}
return 0;
};
;
;
;
完整代碼
#include
#include
#include
//-既然標題是c++,那么就寫成滿滿的c++風格吧
using Color = bool;//-顏色因為只有紅或者黑,選擇bool類型
using KEY_TYPE = int;//-為了更好理解紅黑樹,就不寫成模板類了,所以首選萬年int(笑~)
using VALUE_TYPE = int;//-同理
//-全局靜態紅黑變量
static const Color red = false;
static const Color black = true;
//-紅黑樹的節點特點,有color,有parent
class RBtree_node{
public:
Color color;
RBtree_node * parent;
RBtree_node * left;
RBtree_node * right;
KEY_TYPE key;//-后期如果想解耦合,可以將key和value抽離出去
VALUE_TYPE value;
RBtree_node(Color color_):color(color_),parent(nullptr),left(nullptr),right(nullptr),key(-99999){}
RBtree_node(Color color_, KEY_TYPE key_,RBtree_node * nil):
color(color_),parent(nil),left(nil),right(nil),key(key_){}
};
class RBtree{
private:
//-紅黑樹數據成員:其中nil的意義在于,因為紅黑樹的所有葉子節點都是黑色的,所以可以將所有臨近末尾的節點,
//-都連接到這一個葉子結點nil上,同理,root的parent也可以連接到nil上,形成一個dummy空節點
RBtree_node * root;
RBtree_node * nil;
public :
//-以下實現了紅黑樹常用接口:
//-構造函數
RBtree(){
nil = new RBtree_node(black);//-為所有葉子節點nil初始化,顏色為黑色
root = nil;//-紅黑樹為空的時候,讓nil作為root
}
//-左旋
void leftRotate(RBtree_node *left_node);
//- 右旋
void rightRotate(RBtree_node * right_node);
//-插入key
void insertNode(KEY_TYPE key);
//-修復插入
void fixInsert(RBtree_node * node);
//-查找某個key的節點
RBtree_node* searchNode(KEY_TYPE key);
//-查找某個節點的中序后繼
RBtree_node* successor(RBtree_node * node);
//-刪除key
void deleteNode(KEY_TYPE key);
//-修復刪除
void fixDelete(RBtree_node * node);
//-層序遍歷打印紅黑樹
void print();
//-打印中序遍歷
void printMiddle(RBtree_node * node);
};
//-左旋
void RBtree::leftRotate(RBtree_node *left_node){
RBtree_node * right_node = left_node->right;
//-右節點的左枝條接在左節點的右枝條上
left_node->right = right_node->left;
if(right_node->left!=nil){
left_node->right->parent = left_node;
}
//-右節點接在左節點的父親上
right_node->parent = left_node->parent;
if(left_node == root){
//-nil不會指向任何節點,但是root->parent是nil
root = right_node;
}
else if(left_node == left_node->parent->left){
left_node->parent->left = right_node;
}else{
left_node->parent->right = right_node;
}
//-左節點接在右節點的左枝上
left_node->parent = right_node;
right_node->left = left_node;
}
//- 右旋:寫完左旋后,把所有left和right對調即可
void RBtree::rightRotate(RBtree_node * right_node){
RBtree_node * left_node = right_node->left;
right_node->left = left_node->right;
if(left_node->right!=nil){
right_node->left->parent = right_node;
}
left_node->parent = right_node->parent;
if(right_node == root){
root = left_node;
}
else if(right_node == right_node->parent->right){
right_node->parent->right = left_node;
}else{
right_node->parent->left = left_node;
}
right_node->parent = left_node;
left_node->right = right_node;
}
//-插入key
void RBtree::insertNode(KEY_TYPE key){
RBtree_node * prev = nil;
RBtree_node * cur = root;
while(cur!=nil){
prev = cur;
if(key>cur->key){
cur = cur->right;
}else if(keykey){
cur = cur->left;
}else{//-該key已經存在
return;
}
}
//-創建新節點
RBtree_node * new_node = new RBtree_node(red,key,nil);
//-如果節點沒有元素
new_node->parent = prev;
if(prev == nil){
root = new_node;
}
else if(key key){
prev ->left = new_node;
}else{
prev ->right = new_node;
}
fixInsert(new_node);
print();
}
//-修復插入
void RBtree::fixInsert(RBtree_node * new_node){
while(new_node -> parent->color == red){//-終止條件要注意
//-如果父親是左枝
if(new_node->parent == new_node -> parent->parent->left){
//-獲得其伯父節點
RBtree_node * uncle = new_node->parent->parent->right;
if(uncle->color == red){//-如果伯父是紅色,那么將父親和伯父同時變黑,不會破壞左右平衡
uncle->color = black;
new_node->parent->color = black;
new_node->parent ->parent->color = red;//-將祖父變紅,才能實現下一輪回溯修復
new_node = new_node->parent->parent;
}else{//-如果伯父是黑色
//-判斷new_node是不是右孩子,如果是右孩子轉換成左孩子
if(new_node == new_node -> parent->right){
new_node = new_node->parent;
leftRotate(new_node);
}
//-此時紅色節點是左孩子
//-如果結構本是平衡狀態,右邊本該比左邊多一個黑,但是我們將父親(左)變黑會破壞平衡,
//-所以需要右旋祖父,把父親上浮,相當于在左枝多一個黑的時候給右枝也多了黑,這樣左右就能平衡
new_node->parent->color = black;
new_node->parent ->parent->color = red;
rightRotate(new_node->parent->parent);
}
}
//-如果父親是右枝(將上邊代碼的left和right全部對調即可,不用記規則)
else {
RBtree_node * uncle = new_node->parent->parent->left;
if(uncle->color == red){//-如果伯父是紅色
uncle->color = black;
new_node->parent->color = black;
new_node->parent ->parent->color = red;
new_node = new_node->parent->parent;
}else{//-如果伯父是黑色
if(new_node == new_node -> parent->left){
new_node = new_node->parent;
rightRotate(new_node);
}
new_node->parent->color = black;
new_node->parent ->parent->color = red;
leftRotate(new_node->parent->parent);
}
}
}
//-如果new_node回溯到root,此時root->parent==nil(black)打破了循環,而此時root被改變成了黑色,違反了規則1,
//-所以最后需要強行把root fix成黑色
root->color = black;
}
//-查找某個key的節點
RBtree_node* RBtree::searchNode(KEY_TYPE key){
RBtree_node * cur = root;
while(cur!=nil){
if(key>cur -> key){
cur = cur->right;
}else if(key < cur -> key){
cur = cur->left;
}else{
return cur;
}
}
return cur;
}
//-查找某個節點的中序后繼
RBtree_node* RBtree::successor(RBtree_node * node){
//-如果節點有右孩子
if(node->right!=nil){
RBtree_node * res = node -> right;
while(res->left!=nil){
res = res->left;
}
return res;
}else{
while(node!=root&&node!=node->parent->left){
node = node->parent;
}
return node->parent;
}
}
//-刪除key
void RBtree::deleteNode(KEY_TYPE key){
//-查找key所在節點
RBtree_node * key_node = searchNode(key);
//-實際刪除的節點
RBtree_node* delete_node;
//-delete_node的孩子
RBtree_node* delete_son;
//-如果同時有左枝或者右枝條
if(key_node->left != nil&&key_node->right != nil){
delete_node = successor(key_node);
delete_son = delete_node->right;
}//-如果僅有左枝或者右枝條或者左右都沒有
else{
delete_node = key_node;
if(key_node->left != nil){
delete_son = key_node->left;
}else{
delete_son = key_node->right;
}
}
//-刪除deletenode
delete_son->parent = delete_node->parent;
//-先判斷deletenode是不是根節點
if(delete_node == root){
root = delete_son;
}
else if(delete_node == delete_node->parent->left){
delete_node->parent->left = delete_son;
}else{
delete_node -> parent -> right = delete_son;
}
//-覆蓋key_node原有數據
key_node->key = delete_node -> key;
key_node ->value = delete_node -> value;
//-如果刪除節點是黑色的,需要修復delete_son,注意是孩子
if(delete_node->color == black){
fixDelete(delete_son);
}
//-釋放空間
delete delete_node;
//-打印
print();
}
//-修復刪除
void RBtree::fixDelete(RBtree_node * delete_son){
//-修復的原因是因為delete_son所在的枝條的黑節點比另一個枝條少一個,所以不平衡,所以需要填上左邊缺失的黑,或者減掉右邊多余的黑
//-當delete_son是黑色的一直循環
while(delete_son!=root&&delete_son->color == black){
//-判斷delete_son所在枝條,如果是左枝
if(delete_son == delete_son->parent->left){
//-如果兄弟是紅色的
RBtree_node * bro = delete_son->parent->right;
if(bro->color == red){
bro->color = black;//-兄弟變黑
delete_son->parent->color = red;//-父親變紅
leftRotate(delete_son->parent);//-左旋父親,兄弟上浮,相當于左右都加了一個黑,不改變平衡狀態
bro = delete_son->parent->right;//-新的bro是原來bro的左枝,因為原bro是紅的,其左右枝都是黑色的,這樣保證新的兄弟是黑色的
}
//-此時兄弟是黑色的,判斷兄弟的孩子
//-左黑右黑(兄弟的孩子平衡了)
if(bro->left->color == black&&bro->right -> color == black){
bro->color = red;//-相當于右邊減去多的一個黑,達到平衡
delete_son = delete_son->parent;
}else{
//-如果是左紅右黑,變成左黑右紅
if (bro->right->color == black){
bro -> color = red;
bro->left->color = black;
rightRotate(bro);//-左節點上浮,相當于左右都加了一個黑,不改變平衡
}
bro->color = bro->parent -> color;
bro->parent -> color = black;
bro->right->color = black;//-給右邊加了一個黑
leftRotate(delete_son->parent);//-父親下沉,兄弟上浮,左邊加一個黑,右邊減一個黑,總體上左邊填上了缺少的黑也達到了平衡
delete_son = root;
}
}
//-如果是右枝(不用記規則,把上面的代碼left和right對調即可)
else {
RBtree_node * bro = delete_son->parent->left;
if(bro->color == red){
bro->color = black;
delete_son->parent->color = red;
rightRotate(delete_son->parent);
bro = delete_son->parent->left;
}
if(bro->right->color == black&&bro->left -> color == black){
bro->color = red;
delete_son = delete_son->parent;
}else{
if (bro->left->color == black){
bro -> color = red;
bro->right->color = black;
leftRotate(bro);
}
bro->color = bro->parent -> color;
bro->parent -> color = black;
bro->left->color = black;
rightRotate(delete_son->parent);
delete_son = root;
}
}
}
delete_son->color = black;
}
//-層序遍歷打印紅黑樹
void RBtree::print(){
std::deque dqueue;//-使用deque實現隊列
dqueue.push_back(root);
while(!dqueue.empty()){
int size = (int)dqueue.size();
for (int i = 0; i < size; ++i) {
RBtree_node* temp = dqueue.front();
dqueue.pop_front();
if(temp->left!=nullptr){
dqueue.push_back(temp -> left);
}
if(temp -> right != nullptr){
dqueue.push_back(temp -> right);
}
std::string color = temp->color?"b: ":"r: ";
std::string keystr = temp==nil?"nil":std::to_string(temp->key);
std::cout< }
std::cout< }
}
//-打印中序遍歷
void RBtree::printMiddle(RBtree_node * node){
if(node == nil){
return;
}
printMiddle(node->left);
std::string color = node->color?"b:":"r:";
std::cout
}
int main(){
RBtree rb;
std::string select;
KEY_TYPE key;
while(true){
std::cout<<"n輸入操作:i:插入key,d:刪除key q:退出"< std::cin>>select;
if(select == "i"){
std::cout<<"輸入key"< std::cin>>key;
rb.insertNode(key);
}else if(select == "d"){
std::cout<<"輸入key"< std::cin>>key;
rb.deleteNode(key);
}else if(select == "q"){
break;
}else{
std::cout<<"輸入不合法,重新輸入"< }
}
return 0;
};
;
;
;
<;
<*>
-
內存
+關注
關注
8文章
2902瀏覽量
73534 -
nginx
+關注
關注
0文章
139瀏覽量
12113
發布評論請先 登錄
相關推薦
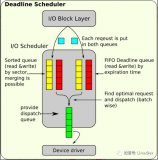
Linux通用塊層之deadline簡介及通用塊層調度器框架
紅魔Mars和黑鯊Helo哪個好
紅魔3和黑鯊2買哪個好
紅魔Mars和黑鯊Helo哪個最好
紅黑樹(Red Black Tree)是一種自平衡的二叉搜索樹




 紅黑樹的特點及應用
紅黑樹的特點及應用











評論