程序實現:
在MATLAB中可采用的語法為:
[K,S,P] = lqr(sys,Q,R,N)
[K,S,P] = lqr(A,B,Q,R,N)
也就是說,目的是計算最佳增益矩陣K
下面以一個例子實現LQR的解法;
M = 85.5; %input 1
m = 8.5; %input 2
b = 0.6;
I = 0.008;
g = 9.8;
l = 0.5;
x0 = [0.2 0 0 0];
a1 = 1;
a2 = 2;
Q = 20;
R=10;
%states = {'x' 'x_dot' 'phi' 'phi_dot'};
p = I*(M+m)+M*m*l^2; %denominator for the A and B matrices
A = [0 1 0 0;
0 -(I+a2*l^2)*b/p (a2^2*g*l^2)/p 0;
0 0 0 1;
0 -(a2*l*b)/p a2*g*l*(a1+a2)/p 0];
B = [ 0;
(I+a2*l^2)/p;
0;
a2*l/p];
[K,S,P] = lqr(A,B,Q,R)
運行可以得到:
K =
-1.4142 -62.4810 67.4838 187.5249
S =
1.0e+05 *
0.0088 0.1913 -0.0265 -0.1230
0.1913 7.3677 -1.0374 -4.8827
-0.0265 -1.0374 0.5767 1.7582
-0.1230 -4.8827 1.7582 5.9016
P =
-0.0262 + 0.0258i
-0.0262 - 0.0258i
-0.4016 + 0.0093i
-0.4016 - 0.0093i
程序可視化:
sys = ss(A,B,eye(4),[0;0;0;0]);
sysclosed = ss(A-B*K,[0;0;0;0],eye(4),[0;0;0;0]);
figure(15)
[ycl,tcl,xcl] = initial(sysclosed,x0);
plot(tcl,ycl(:,1),tcl,ycl(:,2),tcl,ycl(:,3),tcl,ycl(:,4))
title('LQR ')
xlabel('時間')
ylabel('輸出')
legend('x','x_dot','phi','phi_dot')

LQR 啟發式作為基于樣本的運動規劃算法(例如 RRT 或 RRT*)的擴展,可以是相對低成本的距離度量,并在具有復雜或欠驅動動態的域中找到最佳計劃。
% LQR Steer
%===================================
function x_new = LQRSteer( x_nearest, x_rand, K_rand )
% This function contains system's explicit dynamics
global model;
m = model.phy.m;
l = model.phy.l;
b = model.phy.b;
g = model.phy.g;
h = model.h;
u = -K_rand*( x_nearest - x_rand )';
x_dot = [ x_nearest(2), ( u - b*x_nearest(2) - m*g*l*sin(x_nearest(1)) ) ];
x_new = x_nearest + x_dot*h;
end
此MATLAB function可以從來執行系統動力學描述;
% LQR Near
%===================================
function X_near_ids = LQRNear( x_new, S_new, id_nearest )
global GNodes nun;
% Define Neighborhood Radius
gamma = 1; d = 2;
ner = gamma*( log(nun+1)/nun )^(1/d);
% Allocate and Assign to Output
X_near_ids = id_nearest;
for i = 1 : nun
x = GNodes( i, 1:2 );
cost = (x-x_new)*S_new*(x-x_new)';
if cost < ner
X_near_ids(end+1) = i;
end
end
X_near_ids = unique(X_near_ids);
end
輸入期望的初始參數,根據定義算法的邏輯可實現期望數值的求解;
線性二次高斯(LQG)優化控制設計方法,它是線性二次估計器(LQE)(即卡爾曼濾波器)和線性二次調節器(LQR)的組合。
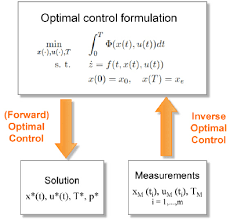
對于逆最優問題,建議讀者閱讀 Zhifei 和 Joo的文章。最優控制理論的逆問題通過二次逼近 (BOBYQA) 技術 的邊界優化來適應和解決。
人工操作任務的成本函數是從給定的演示中建模的,同時考慮與環境的接觸。引入逆Karush-Kuhn-Tucker(KKT)逆最優控制算法來學習具有接觸約束的操縱任務的成本函數。
最優控制理論的主要關注點是找出在滿足某些最優標準的同時將給定系統推向所需狀態的控制信號。
線性二次調節器 (LQR) 是優化控制的一種變體,其中系統動力學由一組線性微分方程建模。此外,最優標準由包含系統狀態和輸入的二次函數描述。
考慮智能體之間的關系,也可以用LQR來求解出最優解;
尋找規定機器人阻抗模型的最佳參數的問題被轉化為線性二次調節器 (LQR) 問題,該問題最大限度地減少了人力并優化了 HRI 系統針對給定任務的閉環行為。
為了避免對人體模型知識的要求,可以使用積分強化學習來解決給定的 LQR 問題。
-
matlab
+關注
關注
182文章
2963瀏覽量
230199 -
機器人
+關注
關注
210文章
28231瀏覽量
206618 -
最優控制
+關注
關注
0文章
9瀏覽量
7142
發布評論請先 登錄
相關推薦
主動隊列管理建模及最優控制策略
什么是工業機器人
辰漢-如何實現服務機器人的運算與控制
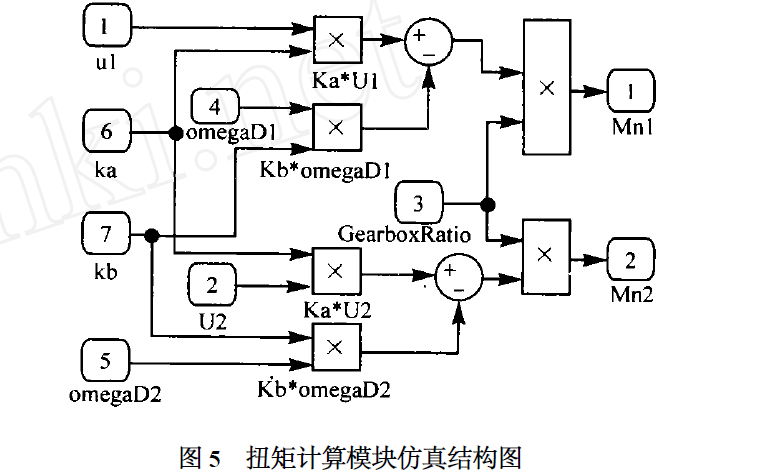
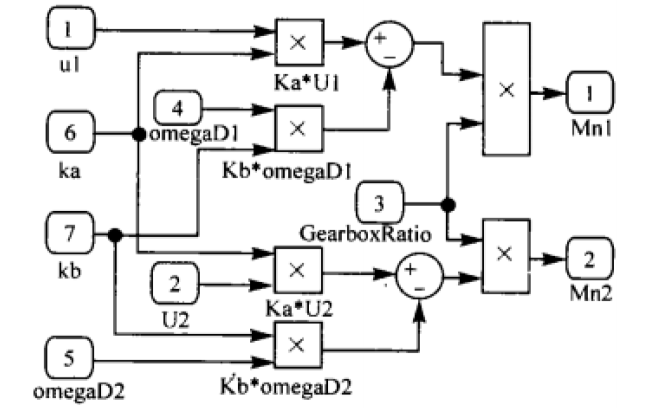
基于Matlab和VR技術的移動機器人建模及仿真
大純滯后對象的最優控制
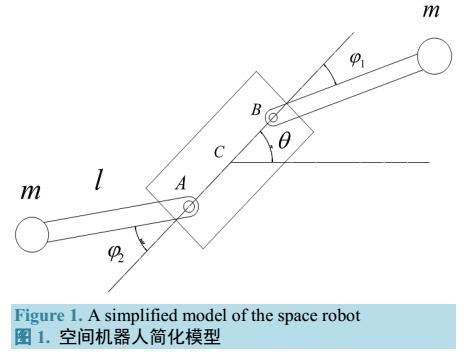
基于Legendre偽譜法的空間機器人姿態運動的最優控制
使用Matlab和VR技術實現移動機器人的建模及仿真的方案說明
如何使用Matlab和VR技術實現移動機器人的建模和仿真




 機器人最優控制的程序實現
機器人最優控制的程序實現
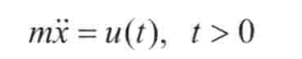










評論