堆的實現思路
什么是堆？
- 堆是一種 基于樹結構的數據結構，它是一棵二叉樹 ，具有以下兩個特點：
- 堆是一個完全二叉樹，即除了最后一層，其他層都是滿的，最后一層從左到右填滿。
- 堆中每個節點都滿足堆的特性，即父節點的值要么等于或者大于（小于）子節點的值。
1.1 堆的分類
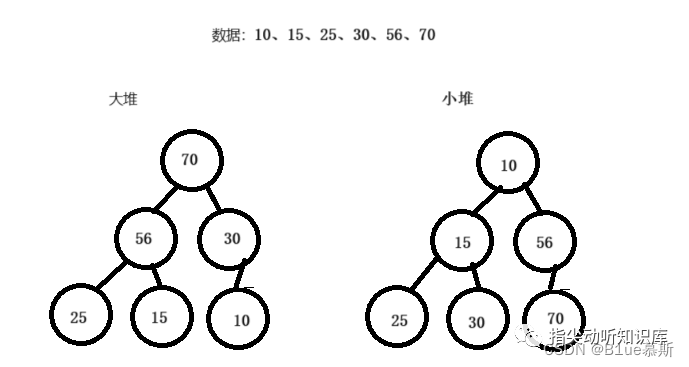
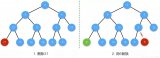
堆一般分為兩類： 大堆和小堆 。
- 大堆中，父節點的值大于或等于子節點的值，
- 小堆中，父節點的值小于或等于子節點的值。
堆的主要應用是在排序和優先隊列中。
以下分別為兩個堆（左大堆，右小堆）：
Part2 堆的實現思路
2.1 使用什么實現？
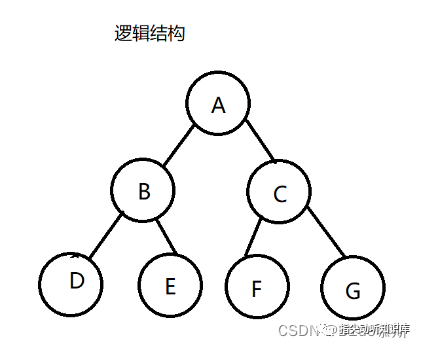
邏輯結構如上， 然而這僅僅是我們想像出來的而已，而實際上的堆的物理結構是一個完全二叉樹 ， 通常是 用數組實現的 。如下：
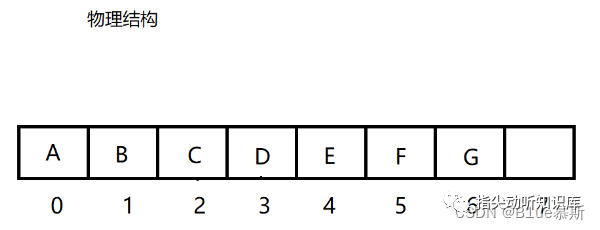
對此，這就要引申出一個問題？我們該如何分辨父節點以及子節點呢？如下：
2.2 怎么分辨父節點以及子節點？
通常我們的數組下標為“0”處即為根節點，也就是說我們一定知道一個父節點！并且我們也有“計算公式”來計算父節點以及子節點。（先記住，后面實現有用！！！）也就是說我們也可以通過公式從每一個位置計算父節點以及子節點！如下：
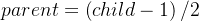
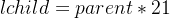
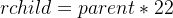
2.3 總體實現思路
先建立一個結構體，由于堆的結構實際上是一顆完全二叉樹，因此我們的 結構跟二叉樹一樣即可！ 接著，想想我們的堆需要實現的功能？ 構建、銷毀、插入、刪除、取堆頂的數據、取數據個數、判空 。(⊙o⊙)…基本的就這些吧哈~
接著按照 定義函數接口->實現各個函數功能->測試測試->收工(-_^) o( ￣▽￣ )ブ
Part3** 堆的實現**
3.1 結構體以及接口的實現
typedefint HPDataType;
typedefstruct Heap
{
HPDataType* _a;
int _size;
int _capacity;
}Heap;
// 堆的構建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的銷毀
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的刪除
void HeapPop(Heap* hp);
// 取堆頂的數據
HPDataType HeapTop(Heap* hp);
// 堆的數據個數
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
3.2 堆的兩種建堆方式
在實現以上的接口之前，我們必須要知道堆的兩種建堆方式！！！
并且僅僅通過調整建堆方式的<和>符號，我們就可以輕易控制大小堆，具體看代碼注釋！
建堆有兩種方式，分別是 自底向上建堆以及自頂向下建堆。 具體簡介如下：
- 自底向上建堆：自底向上建堆是指按照原始數組順序依次插入元素，然后對每個插入的元素執行向上調整的操作，使得堆的性質保持不變。這種方法需要對每個元素都進行調整操作，時間復雜度為 O(nlogn)。
- 自頂向下建堆：自頂向下建堆是指從堆頂開始，對每個節點執行向下調整操作，使得堆的性質保持不變。這種方法需要從根節點開始遞歸向下調整，時間復雜度為 O(n)。因此，自頂向下建堆的效率比自底向上建堆要高。
以上兩種建堆方式，實際上是基于兩種調整方法，接下來將詳細介紹：
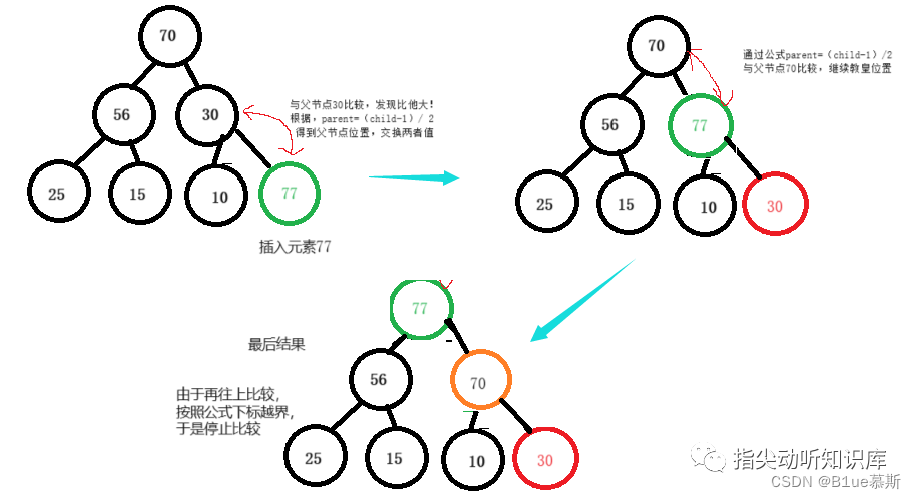
向上調整方法
堆的向上調整方法將新插入的節點從下往上逐層比較，如果當前節點比其父節點大（或小，根據是大根堆還是小根堆），則交換這兩個節點。一直向上比較，直到不需要交換為止。這樣可以保證堆的性質不變。
具體步驟如下：
- 將新插入的節點插入到堆的最后一位。
- 獲取該節點的父節點的位置，比較該節點與其父節點的大小關系。
- 如果該節點比其父節點大（或小，根據是大根堆還是小根堆），則交換這兩個節點。
- 重復步驟2-3，直到不需要交換為止，堆的向上調整完成。
- 堆的向上調整的時間復雜度為O(logn)，其中n為堆的大小。
一圖讓你了解~：
實現如下：
void swap(HPDataType* s1, HPDataType* s2)
{
HPDataType temp = *s1;
*s1 = *s2;
*s2 = temp;
}
void Adjustup(HPDataType* a, int child)//向上調整
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])//建大堆，小堆則<
{
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
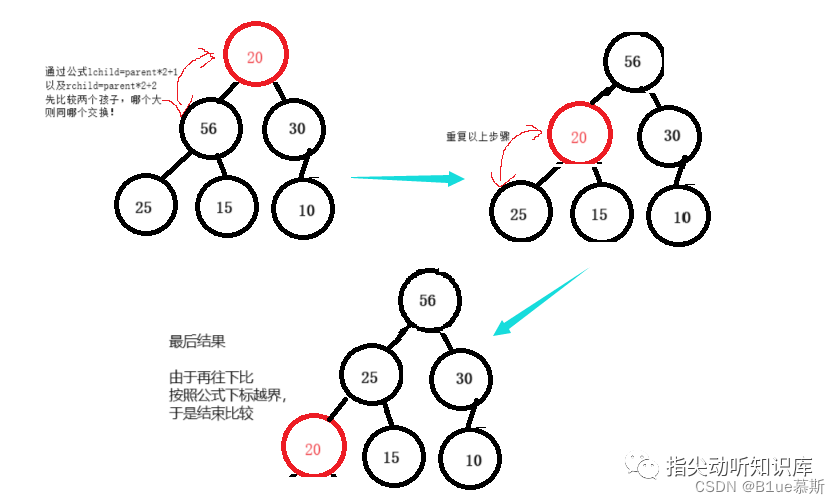
向下調整方法
堆的向下調整方法是指將某個節點的值下放至其子節點中，以維護堆的性質的過程。
假設當前節點為 i，其左子節點為 2i+1，右子節點為 2i+2，堆的大小為 n
則向下調整的步驟如下：
- 從當前節點 i 開始，將其與其左右子節點中較小或較大的節點比較，找出其中最小或最大的節點 j。
- 如果節點 i 小于等于（或大于等于，取決于是最小堆還是最大堆）節點 j，則說明它已經滿足堆的性質，調整結束；否則，將節點 i 與節點 j 交換位置，并將當前節點 i 更新為 j。
- 重復執行步驟 1 和步驟 2，直到節點 i 沒有子節點或已經滿足堆的性質。
一圖讓你了解~：
實現如下：
void swap(HPDataType* s1, HPDataType* s2)
{
HPDataType temp = *s1;
*s1 = *s2;
*s2 = temp;
}
void Adjustdown(HPDataType* a, int n, int parent)//向下調整
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] > a[child])//找出兩個孩子中較大的那個，此為大堆，如果要實現小堆則 改 >
{
++child;
}
if (a[child] > a[parent])//此為大堆，如果要實現小堆則 改 >
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
3.3 堆的構建
void HeapCreate(Heap* hp, HPDataType* a, int n)
{
assert(hp);
assert(a);
hp- >_a = (HPDataType*)malloc(sizeof(HPDataType) * n);
if (!hp- >_a)
{
perror("malloc fail");
exit(-1);
}
hp- >_capacity = hp- >_size = n;
//將a中的元素全部轉移到堆中
memcpy(hp- >_a, a, sizeof(HPDataType) * n);
//建堆
for (int i = 1; i < n; i++)
{
Adjustup(hp- >_a, i);//按向上調整，此建立大堆
}
}
本文的構建方法是 通過傳遞一個數組以及傳遞一個數組大小來構建的 ，里面包括了堆結構體的初始化操作，基本的建堆方式則是通過向上調整方法建堆。
3.4 堆的銷毀
void HeapDestory(Heap* hp)
{
assert(hp);
free(hp- >_a);
hp- >_a = NULL;
hp- >_capacity = hp- >_size = 0;
}
就正常的銷毀操作？大家應該都懂（確信） (o°ω°o)
3.5 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
if (hp- >_capacity == hp- >_size)//擴容
{
int newcapacity = hp- >_capacity == 0 ? 4 : hp- >_capacity * 2;
HPDataType* new = (HPDataType*)realloc(hp- >_a, sizeof(HPDataType) * newcapacity);
if (!new)
{
perror("realloc fail");
exit(-1);
}
hp- >_a = new;
hp- >_capacity = newcapacity;
}
hp- >_a[hp- >_size++] = x;
Adjustup(hp- >_a, hp- >_size - 1);
}
實現是對于堆的空間進行判斷，不夠則是擴容操作，當然也有初始化的意思，接著是通過向上調整的方式插入操作。
3.6 堆的刪除（較重要）
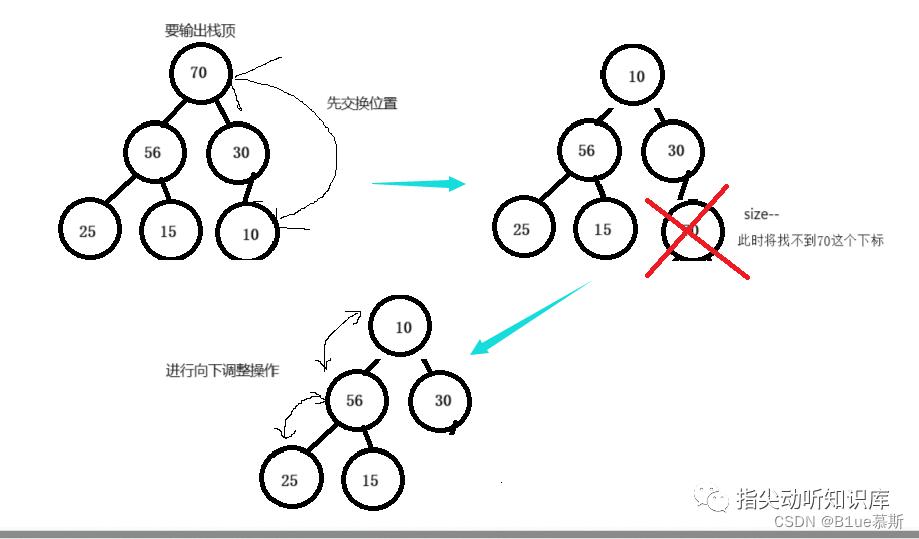
void HeapPop(Heap* hp)//先將最后一個數與堆頂交換，然后再讓size--，再進行向下調整
{
assert(hp);
swap(&hp- >_a[0], &hp- >_a[hp- >_size - 1]);
hp- >_size--;
Adjustdown(hp- >_a, hp- >_size, 0);
}
進行刪除操作，我們當然是刪除堆頂啦，這個刪除操作先將最后一個數與堆頂交換，然后再讓size--，再進行向下調整。
一圖讓你了解~：
3.7 取堆頂的數據
HPDataType HeapTop(Heap* hp)//取堆頂
{
assert(hp);
assert(hp- >_size > 0);
return hp- >_a[0];
}
3.8 堆的數據個數
int HeapSize(Heap* hp)//堆大小
{
assert(hp);
return hp- >_size;
}
3.9 堆的判空
int HeapEmpty(Heap* hp)//判堆空
{
assert(hp);
return hp- >_size==0;
}
Part4 總體代碼
4.1pile.h
#pragma once
#define _CRT_SECURE_NO_WARNINGS 01
#include< stdio.h >
#include< stdlib.h >
#include< string.h >
#include< assert.h >
typedefint HPDataType;
typedefstruct Heap
{
HPDataType* _a;
int _size;
int _capacity;
}Heap;
// 堆的構建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的銷毀
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的刪除
void HeapPop(Heap* hp);
// 取堆頂的數據
HPDataType HeapTop(Heap* hp);
// 堆的數據個數
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
4.2pile.c
#include"pile.h"
void swap(HPDataType* s1, HPDataType* s2)
{
HPDataType temp = *s1;
*s1 = *s2;
*s2 = temp;
}
void Adjustup(HPDataType* a, int child)//向上調整
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])//建大堆，小堆則<
{
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void Adjustdown(HPDataType* a, int n, int parent)//向下調整
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] > a[child])//找出兩個孩子中較大的那個，此為大堆，如果要實現小堆則 改 >
{
++child;
}
if (a[child] > a[parent])//此為大堆，如果要實現小堆則 改 >
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapCreate(Heap* hp, HPDataType* a, int n)
{
assert(hp);
assert(a);
hp- >_a = (HPDataType*)malloc(sizeof(HPDataType) * n);
if (!hp- >_a)
{
perror("malloc fail");
exit(-1);
}
hp- >_capacity = hp- >_size = n;
//將a中的元素全部轉移到堆中
memcpy(hp- >_a, a, sizeof(HPDataType) * n);
//建堆
for (int i = 1; i < n; i++)
{
Adjustup(hp- >_a, i);//按向上調整，此建立大堆
}
}
void HeapDestory(Heap* hp)
{
assert(hp);
free(hp- >_a);
hp- >_a = NULL;
hp- >_capacity = hp- >_size = 0;
}
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
if (hp- >_capacity == hp- >_size)//擴容
{
int newcapacity = hp- >_capacity == 0 ? 4 : hp- >_capacity * 2;
HPDataType* new = (HPDataType*)realloc(hp- >_a, sizeof(HPDataType) * newcapacity);
if (!new)
{
perror("realloc fail");
exit(-1);
}
hp- >_a = new;
hp- >_capacity = newcapacity;
}
hp- >_a[hp- >_size++] = x;
Adjustup(hp- >_a, hp- >_size - 1);
}
void HeapPop(Heap* hp)//先將最后一個數與堆頂交換，然后再讓size--，再進行向下調整
{
assert(hp);
swap(&hp- >_a[0], &hp- >_a[hp- >_size - 1]);
hp- >_size--;
Adjustdown(hp- >_a, hp- >_size, 0);
}
HPDataType HeapTop(Heap* hp)//取堆頂
{
assert(hp);
assert(hp- >_size > 0);
return hp- >_a[0];
}
int HeapSize(Heap* hp)//堆大小
{
assert(hp);
return hp- >_size;
}
int HeapEmpty(Heap* hp)//判堆空
{
assert(hp);
return hp- >_size==0;
}
4.3test.c
#include"pile.h"
void test()
{
Heap hp;
int arr[] = { 1,6,2,3,4,7,5 };
HeapCreate(&hp, arr, sizeof(arr) / sizeof(arr[0]));
//HeapPush(&hp, 10);
printf("%dn", HeapSize(&hp));
while (!HeapEmpty(&hp))
{
printf("%d %d n", HeapTop(&hp), HeapSize(&hp));
HeapPop(&hp);
}
printf("%dn", HeapSize(&hp));
HeapDestory(&hp);
HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
printf("n");
}
int main()
{
test();
return0;
}
4.4 測試結果
聲明：本文內容及配圖由入駐作者撰寫或者入駐合作網站授權轉載。文章觀點僅代表作者本人，不代表電子發燒友網立場。文章及其配圖僅供工程師學習之用，如有內容侵權或者其他違規問題，請聯系本站處理。
舉報投訴
-
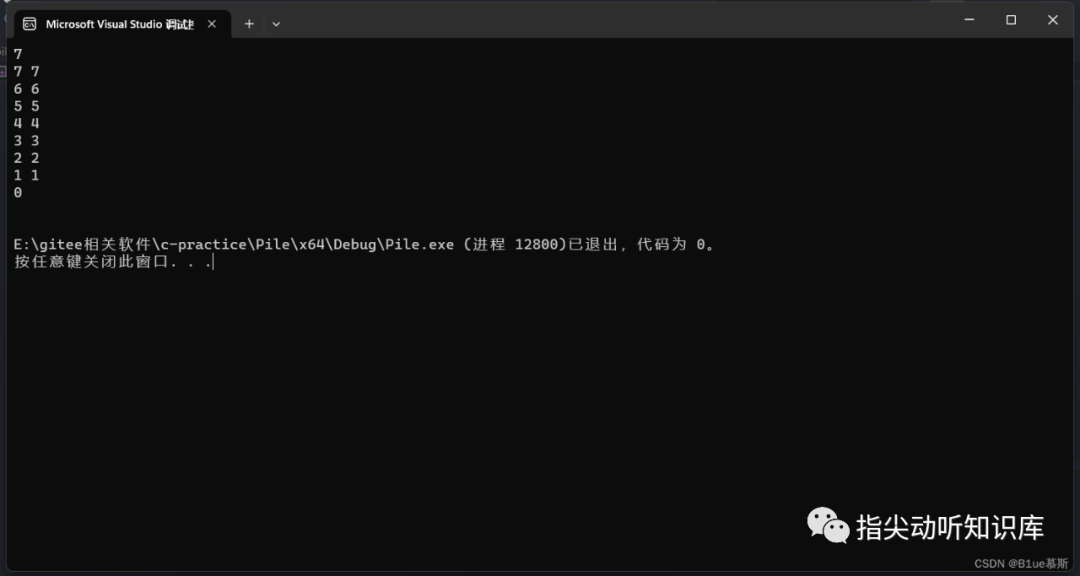
接口
+關注
關注
33文章
8497瀏覽量
150834 -
數據結構
+關注
關注
3文章
573瀏覽量
40093 -
元素
+關注
關注
0文章
47瀏覽量
8421 -
二叉樹
+關注
關注
0文章
74瀏覽量
12311
發布評論請先 登錄
相關推薦
堆煤傳感器的工作原理是什么？
堆煤傳感器正常時煤位傳感器輸出端“堆煤”輸出高電平，當煤位增高推移傳感器偏轉一定角度時，其內萬向接點導通， “堆煤”輸出低電平，“滿煤”指示燈亮，經短暫延時，主機執行繼電器釋放，實現
發表于 03-31 09:00
如何使用鏈接腳本刪除堆分配？
的 heap_symbol），這對我來說會更好，因為否則這個符號會得到它的地址，并且可以使用它的地址覆蓋內存。我的問題是，當我只是丟棄它時，我得到了期望此引用的 gcc 文件 (_cr_sbrk.c) 的引用錯誤。我想尋求幫助來實現我的目標，即安全地從鏈接器中刪除堆分配
發表于 03-23 07:05
整流堆,什么是整流堆
整流堆,什么是整流堆
橋堆的檢測
1. 全橋的檢測 大多數的整流全橋上，均標注有“+”、“-”、“~”符號（其中“+”為整流后輸出電壓
發表于 02-27 10:46
?2122次閱讀
串口WiFi模塊實現遠程控制電飯煲的設計思路分享.pdf
分享一個串口WiFi模塊實現遠程控制電飯煲的設計思路，通過串口wifi模塊可以在手機app上遠程操控電飯煲，相比定時的效果更好！
發表于 04-26 16:57
?76次下載
什么是堆內存？堆內存是如何分配的？
在一般的編譯系統中，堆內存的分配方向和棧內存是相反的。當棧內存從高地址向低地址增長的時候，堆內存從低地址向高地址分配。
實現完全 MCU 分區隔離：堆
曾幾何時，嵌入式系統非常簡單以至于很少使用堆。然而，從那時起，復雜性增長得如此之快，以至于大多數嵌入式系統，甚至是實時操作系統，現在都使用堆。如果只有一個堆在使用，堆效率就不是什么大問
發表于 11-26 15:21
?20次下載
橋堆的作用是什么？橋堆整流后電壓是多少?
橋堆的作用及工作原理解讀 橋堆的作用是什么？橋堆整流后電壓是多少?? 橋堆是一種常用的電路，廣泛應用于電力電子系統中。橋堆是一種全波整流電路
UVC bulk傳輸實現思路
前段時間有個讀者咨詢UVC bulk 傳輸實現，接著這個機會重新梳理一遍UVC bulk 傳輸實現思路,同時對比ISO 與 Bulk 實現不同。
如何使用SystemView的堆監控功能
SystemView能夠監視應用程序如何使用動態存儲。這意味著，如果應用程序中使用了C或C++堆、自定義堆或RTOS提供的內存池對象，我們可以跟蹤這些對象的使用情況。SystemView可以在一個
工商網監
評論